Основная логическая характеристика суждения (лекция 3)

1.

Пролог
КАЖДОМУ НАДО
ИМЕТЬ СВОЕ
СУЖДЕНИЕ
ЦИЦЕРОН

2.

3.

ПЛАН ЛЕКЦИИ
1. Общая характеристика суждений
2. Простые суждения: состав, логические свойства
и виды
3.
Сложные
суждения:
структура,
виды,
истинностные значения логических связок.
4. Отношения между суждениями
5. Отрицание суждений

4.

Вопрос №1.
Общая характеристика
суждений

5.

Суждение – это форма мышления, с помощью которой
в сознании отражаются предметы в их связях и
отношениях
В
естественном
языке
суждения
выражаются
в
форме
президентская
форма
повествовательных предложений (высказываний)
Пример:
«Иванов - адвокат».
«Владимир – брат Сергея».
«В
некоторых
странах
существует
правления»
«На улице идет снег и дует сильный ветер»

6.

ОСНОВНАЯ ЛОГИЧЕСКАЯ ХАРАКТЕРИСТИКА СУЖДЕНИЯ –
его истинностное значение
ИСТИННОСТЬ
- Соответствие содержания
суждения действительности
ЛОЖНОСТЬ
- Несоответствие содержания
суждения действительности

7.

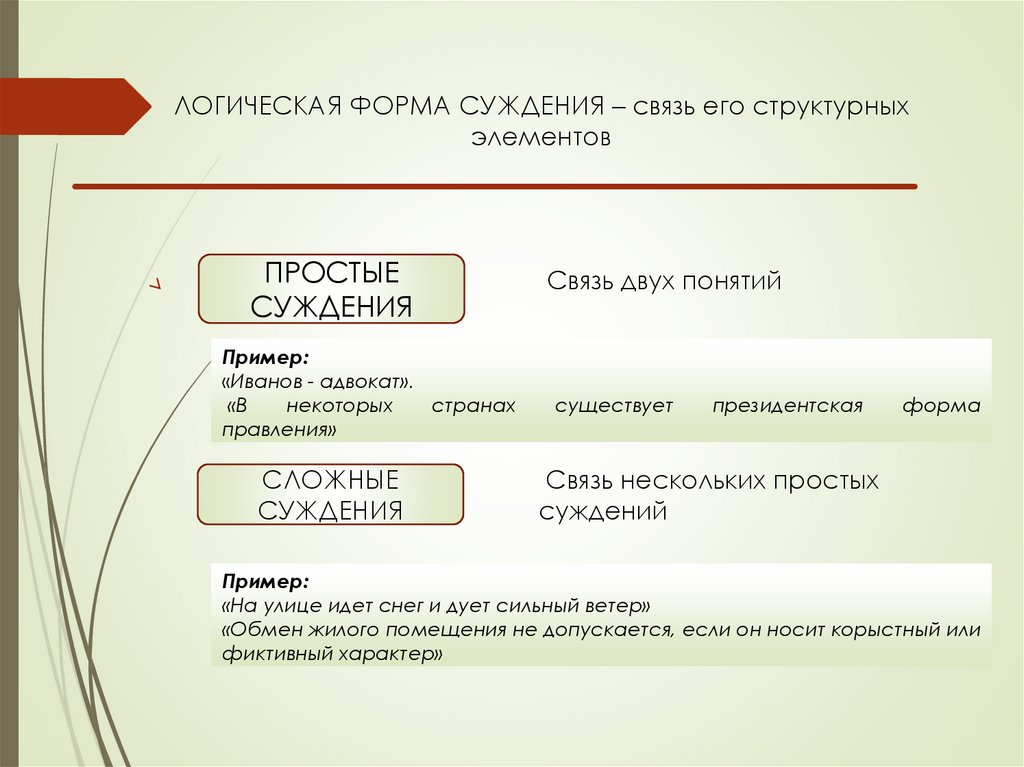
ЛОГИЧЕСКАЯ ФОРМА СУЖДЕНИЯ – связь его структурных
элементов
ПРОСТЫЕ
СУЖДЕНИЯ
Пример:
«Иванов - адвокат».
«В
некоторых
странах
правления»
СЛОЖНЫЕ
СУЖДЕНИЯ
Связь двух понятий
существует
президентская
форма
Связь нескольких простых
суждений
Пример:
«На улице идет снег и дует сильный ветер»
«Обмен жилого помещения не допускается, если он носит корыстный или
фиктивный характер»

8.

2. Простые суждения: состав,
логические свойства и виды

9.

Простое суждение
- суждение, составными частями которого являются два понятия
В естественном языке выражаются распространенными и
нераспространенными простыми предложениями
Пример:
«адвокат» – «человек, живущий в Москве»
«Все адвокаты живут в Москве»
«Все адвокаты не живут в Москве»
«Некоторые адвокаты живут в Москве»
«Некоторые адвокаты не живут в Москве»

10.

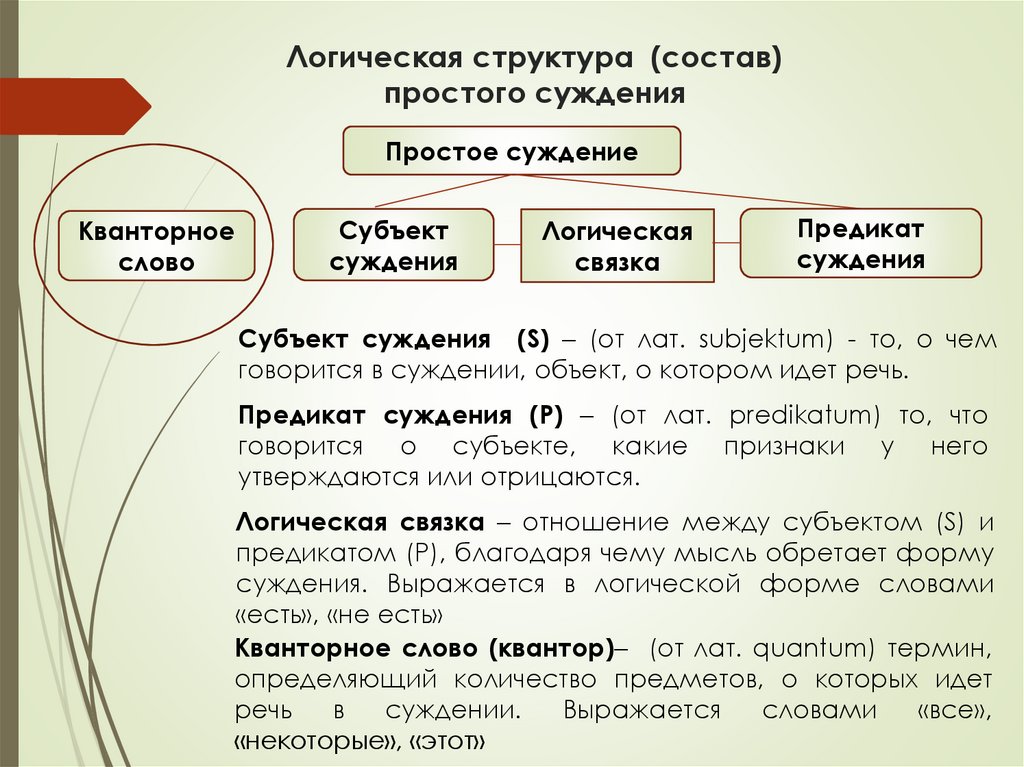
Логическая структура (состав)
простого суждения
Простое суждение
Кванторное
слово
Субъект
суждения
Логическая
связка
Предикат
суждения
Субъект суждения (S) – (от лат. subjektum) - то, о чем
говорится в суждении, объект, о котором идет речь.
Предикат суждения (P) – (от лат. predikatum) то, что
говорится о субъекте, какие признаки у него
утверждаются или отрицаются.
Логическая связка – отношение между субъектом (S) и
предикатом (P), благодаря чему мысль обретает форму
суждения. Выражается в логической форме словами
«есть», «не есть»
Кванторное слово (квантор)– (от лат. quantum) термин,
определяющий количество предметов, о которых идет
речь
в
суждении.
Выражается
словами
«все»,
«некоторые», «этот»

11.

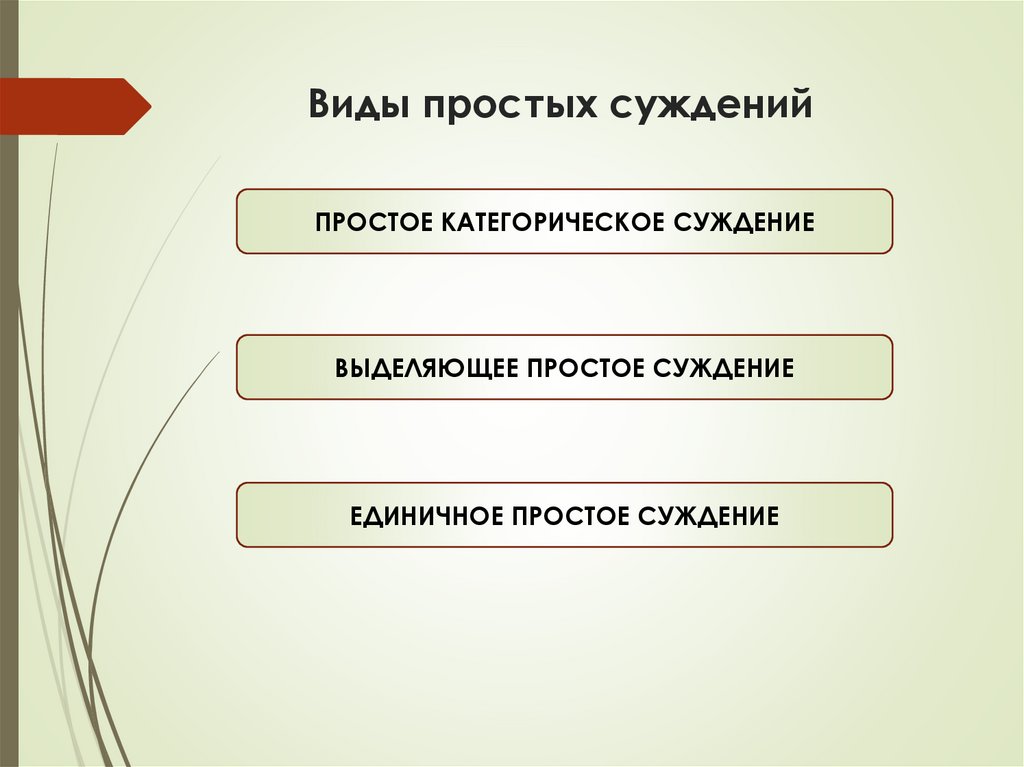
Виды простых суждений
ПРОСТОЕ КАТЕГОРИЧЕСКОЕ СУЖДЕНИЕ
ВЫДЕЛЯЮЩЕЕ ПРОСТОЕ СУЖДЕНИЕ
ЕДИНИЧНОЕ ПРОСТОЕ СУЖДЕНИЕ

12.

Количественная характеристика
категорических суждений
На количество суждения указывает кванторное слово
-суждения, в которых что-либо утверждается
или отрицается в отношении всех элементов
объема субъекта. Квантор «все» - квантор
общности
ОБЩИЕ
«Каждый имеет право на жизнь»;
«Все работники прошли медицинский осмотр»;
«Ни один игрок нашей команды не травмировался»;
«Всякий грамотный человек обнаружит такую ошибку»
……..«Юристы имеют специальное образование»
ЧАСТНЫЕ
- суждения, в которых что-либо утверждается
или отрицается в отношении некоторых
элементов
объема
субъекта.
Квантор
«некоторые» - квантор существования
«Большинство студентов сдали этот экзамен»;
«Ряд экономических реформ был проведен в России в 90-ые годы»;
«Некоторые птицы улетают зимовать в теплые края»;
«Множество огней вспыхнули одновременно»;
«По большей части дни этой зимы были морозными »;
……….«Древние греки внесли большой вклад в развитие логики»

13.

Качественная характеристика
категорических суждений
На качество суждения указывает глагол-связка, стоящий между
субъектом и предикатом суждения.
УТВЕРДИТЕЛЬНЫЕ
суждения, в которых логическая связь
выражена словами «есть», «является» или
знаком препинания- тире.
«Каждый первоклассник является учеником»;
«Некоторые студенты - спортсмены»;
«Всякое число есть математический знак»
ОТРИЦАТЕЛЬНЫЕ
- суждения, в которых логическая связь
выражена словами «не есть», «не является»,
«не».
«Некоторые приговоры суда не являются
обвинительными».
«Некоторые студенты не пришли на занятия»
Суждения с отрицательным понятием на месте предиката, но
утвердительной связкой рассматривается как утвердительное
«Этот человек недобрый»

14.

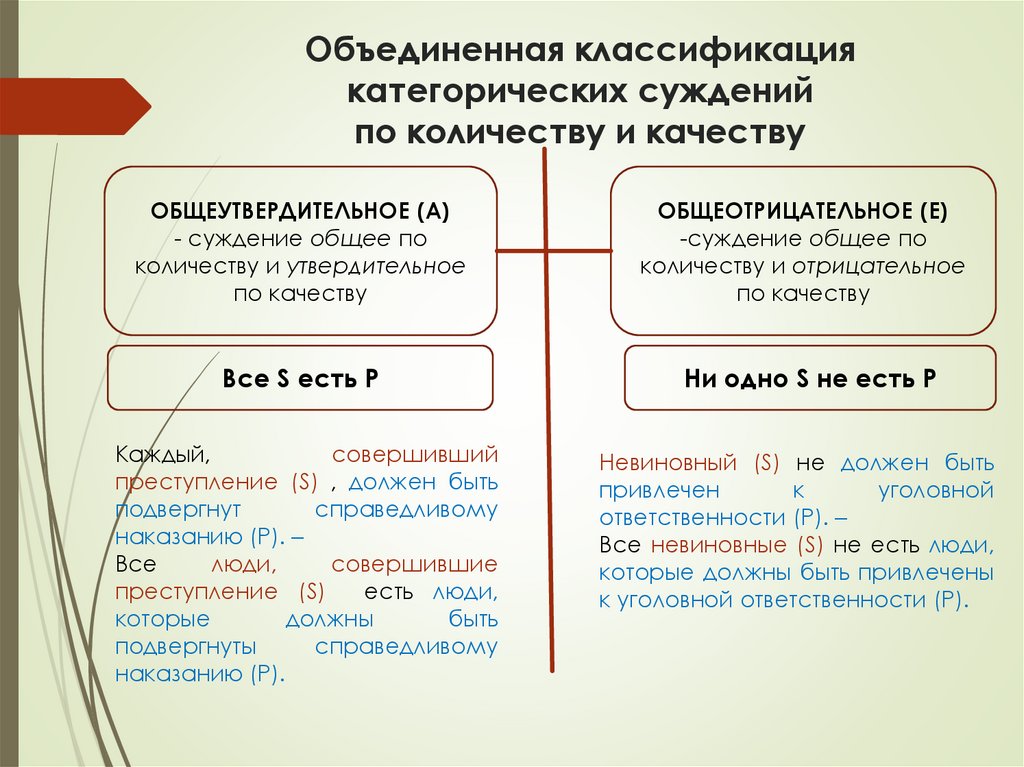
Объединенная классификация
категорических суждений
по количеству и качеству
ОБЩЕУТВЕРДИТЕЛЬНОЕ (А)
- суждение общее по
количеству и утвердительное
по качеству
ОБЩЕОТРИЦАТЕЛЬНОЕ (Е)
-суждение общее по
количеству и отрицательное
по качеству
Все S есть P
Ни одно S не есть P
Каждый,
совершивший
преступление (S) , должен быть
подвергнут
справедливому
наказанию (Р). –
Все
люди,
совершившие
преступление (S)
есть люди,
которые
должны
быть
подвергнуты
справедливому
наказанию (Р).
Невиновный (S) не должен быть
привлечен
к
уголовной
ответственности (Р). –
Все невиновные (S) не есть люди,
которые должны быть привлечены
к уголовной ответственности (Р).

15.

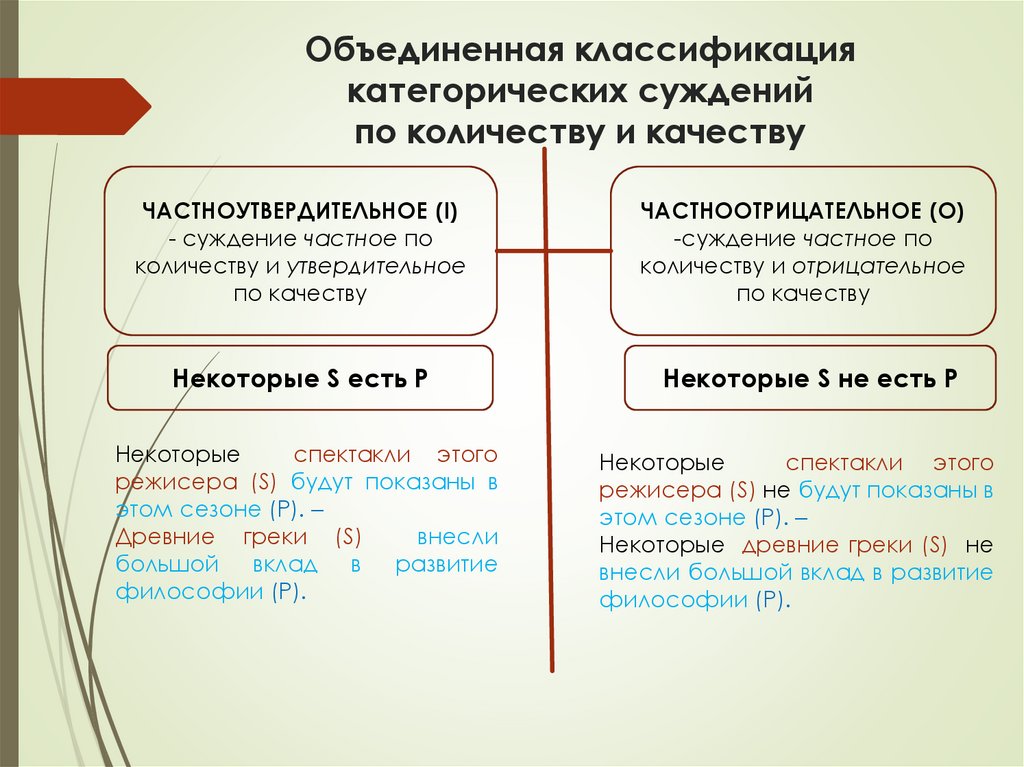
Объединенная классификация
категорических суждений
по количеству и качеству
ЧАСТНОУТВЕРДИТЕЛЬНОЕ (I)
- суждение частное по
количеству и утвердительное
по качеству
ЧАСТНООТРИЦАТЕЛЬНОЕ (О)
-суждение частное по
количеству и отрицательное
по качеству
Некоторые S есть P
Некоторые S не есть P
Некоторые
спектакли этого
режисера (S) будут показаны в
этом сезоне (Р). –
Древние греки (S)
внесли
большой вклад в развитие
философии (Р).
Некоторые
спектакли этого
режисера (S) не будут показаны в
этом сезоне (Р). –
Некоторые древние греки (S) не
внесли большой вклад в развитие
философии (Р).

16.

Единичные суждения
- это суждения, в которых признак, выраженный в
предикате, принадлежит (или не принадлежит) субъекту,
выраженному единичным понятием.
Этот S есть P
Этот S не есть P
«Аристотель был учителем Александра
Македонского».
«Иванов не является свидетелем по делу».

17.

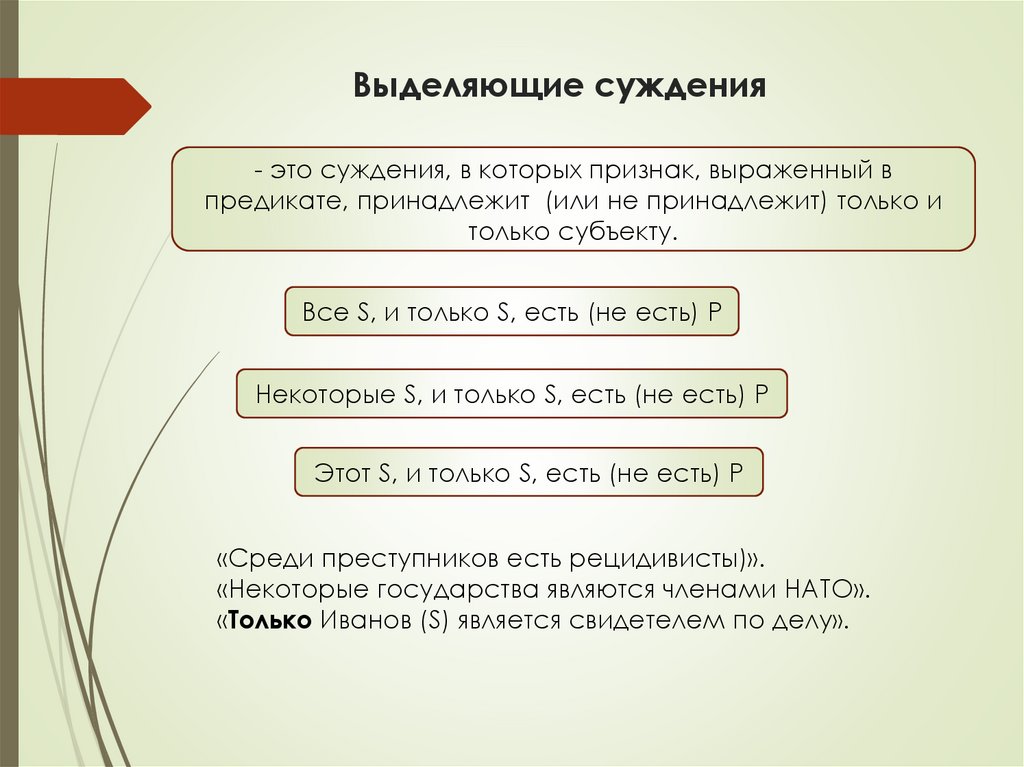
Выделяющие суждения
- это суждения, в которых признак, выраженный в
предикате, принадлежит (или не принадлежит) только и
только субъекту.
Все S, и только S, есть (не есть) P
Некоторые S, и только S, есть (не есть) P
Этот S, и только S, есть (не есть) P
«Среди преступников есть рецидивисты)».
«Некоторые государства являются членами НАТО».
«Только Иванов (S) является свидетелем по делу».

18.

Распределенность терминов в суждении
Термин является распределенным, если он взят в полном объеме;
обозначается со знаком «+» (S+; P+)
Термин является нераспределенным, если он взят в части
объема; обозначается со знаком «-» (S-; P- )

19.

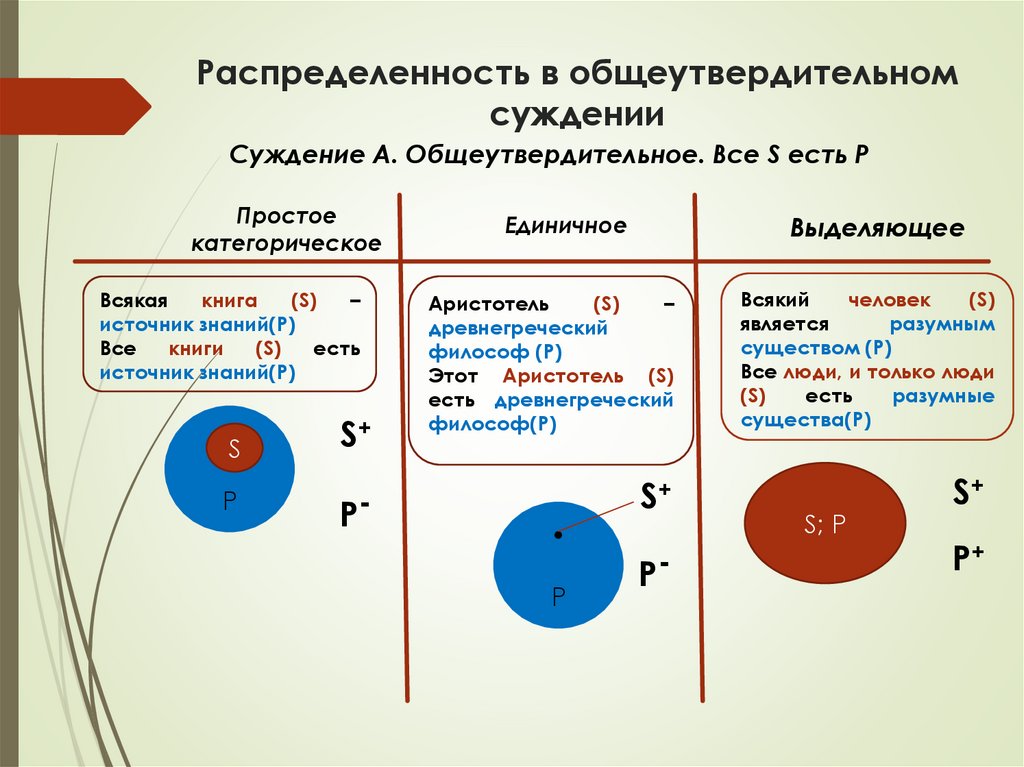
Распределенность в общеутвердительном
суждении
Суждение А. Общеутвердительное. Все S есть P
Простое
категорическое
Всякая
книга
(S)
–
источник знаний(P)
Все
книги
(S)
есть
источник знаний(P)
S
P
S+
P-
Единичное
Выделяющее
Аристотель
(S)
–
древнегреческий
философ (P)
Этот Аристотель (S)
есть древнегреческий
философ(P)
Всякий
человек
(S)
является
разумным
существом (P)
Все люди, и только люди
(S)
есть
разумные
существа(P)
S+
S+
P
P-
S; P
P+

20.

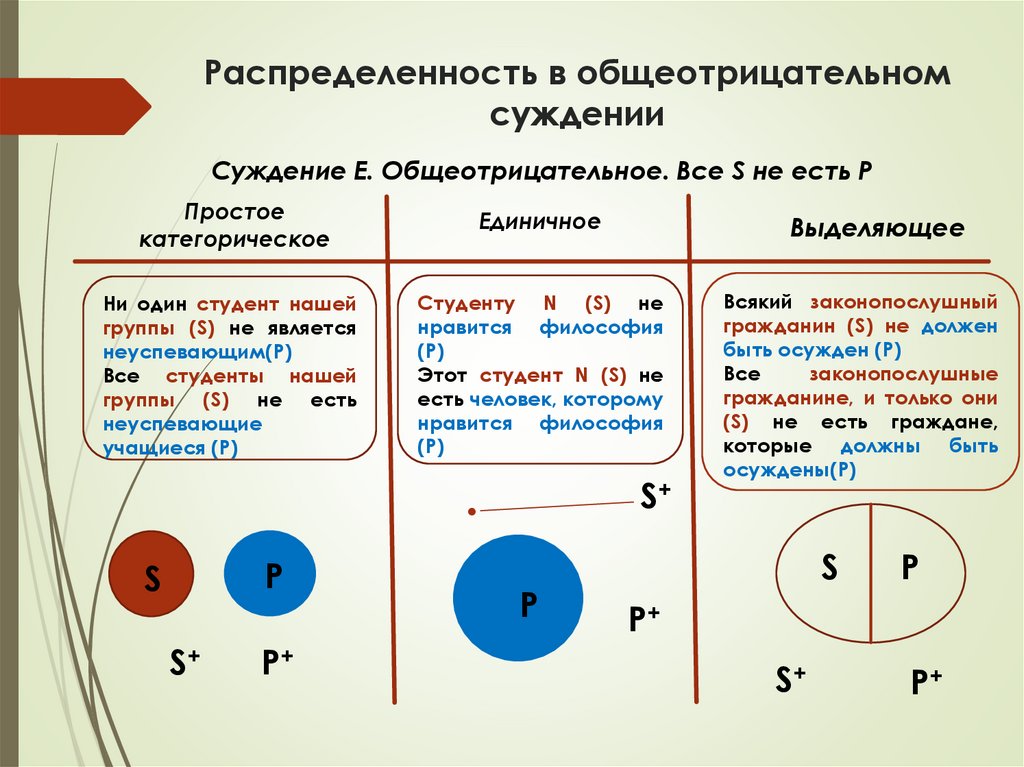
Распределенность в общеотрицательном
суждении
Суждение Е. Общеотрицательное. Все S не есть P
Простое
категорическое
Единичное
Ни один студент нашей
группы (S) не является
неуспевающим(P)
Все студенты нашей
группы (S) не есть
неуспевающие
учащиеся (P)
Студенту N (S) не
нравится философия
(P)
Этот студент N (S) не
есть человек, которому
нравится философия
(P)
S+
P
S
S+
P+
Выделяющее
P
Всякий законопослушный
гражданин (S) не должен
быть осужден (P)
Все
законопослушные
гражданине, и только они
(S) не есть граждане,
которые должны быть
осуждены(P)
S
P
P+
S+
P+

21.

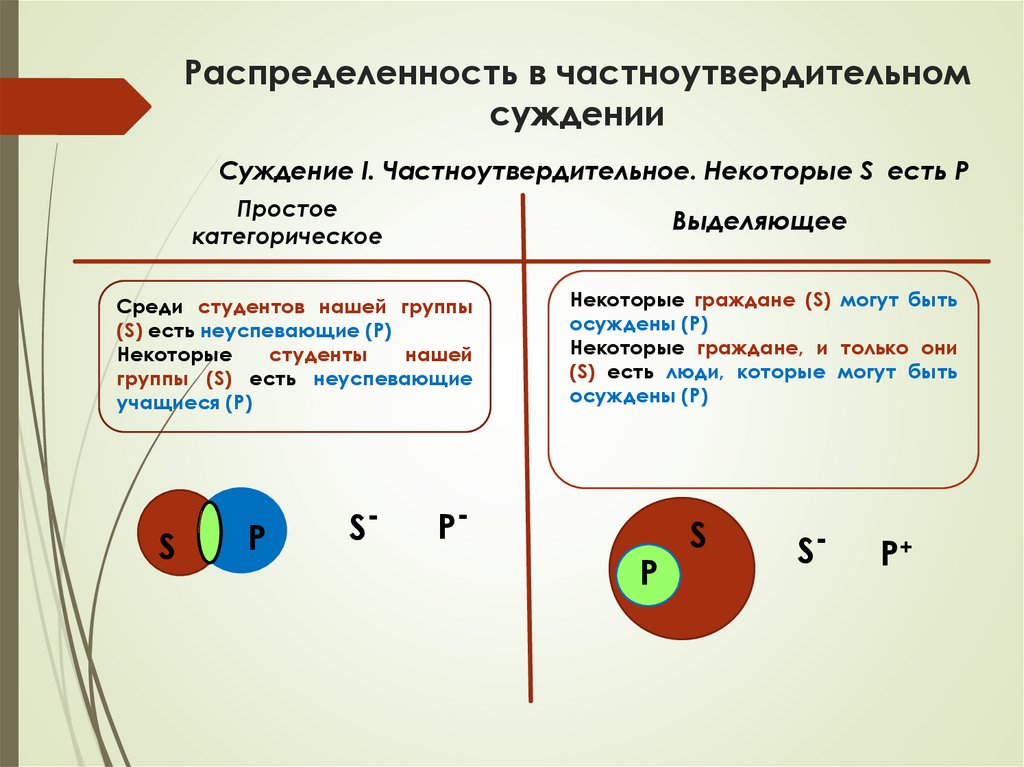
Распределенность в частноутвердительном
суждении
Суждение I. Частноутвердительное. Некоторые S есть P
Простое
категорическое
Выделяющее
Среди студентов нашей группы
(S) есть неуспевающие (P)
Некоторые
студенты
нашей
группы (S) есть неуспевающие
учащиеся (P)
Некоторые граждане (S) могут быть
осуждены (P)
Некоторые граждане, и только они
(S) есть люди, которые могут быть
осуждены (P)
S
P
S-
P-
P
S
P
S-
P+

22.

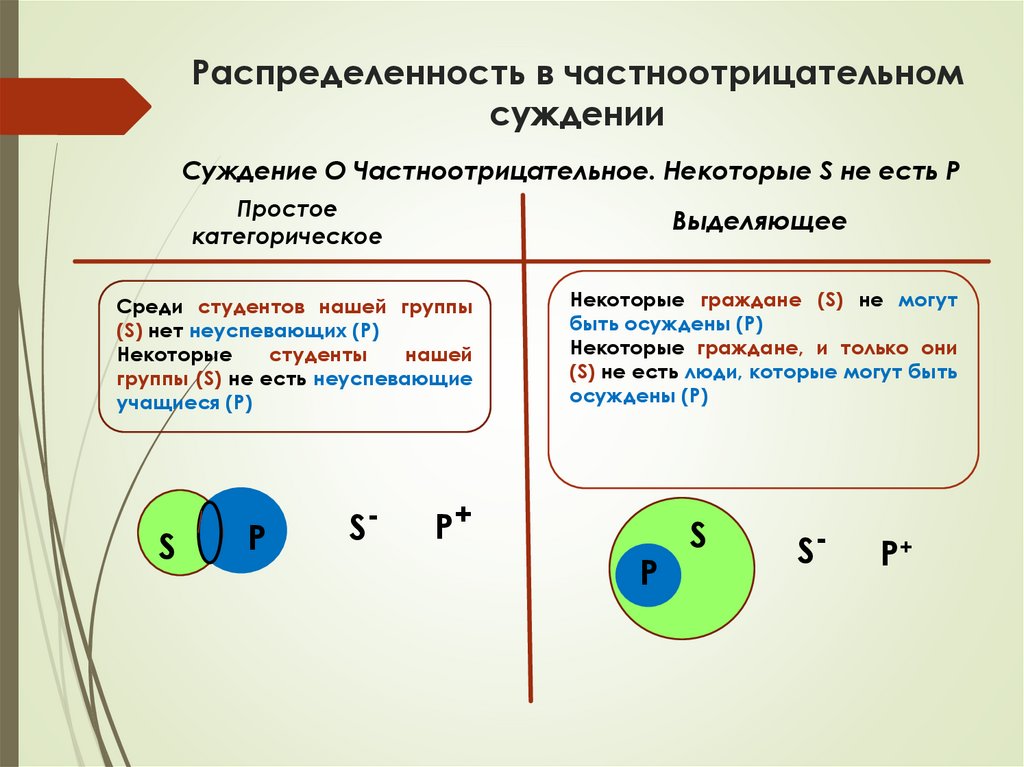
Распределенность в частноотрицательном
суждении
Суждение О Частноотрицательное. Некоторые S не есть P
Простое
категорическое
Выделяющее
Среди студентов нашей группы
(S) нет неуспевающих (P)
Некоторые
студенты
нашей
группы (S) не есть неуспевающие
учащиеся (P)
Некоторые граждане (S) не могут
быть осуждены (P)
Некоторые граждане, и только они
(S) не есть люди, которые могут быть
осуждены (P)
S
P
S-
P+
P
S
P
S-
P+

23.

Распределенность терминов в
простых суждениях
Логическая форма
суждения
Буквенное
обозначение
S
P
P выд.
Все S есть P
A
+
-
+
Все S не есть P
E
+
+
+
Некоторые S есть P
I
-
-
+
Некоторые S не есть P
O
-
+
+
На распределенность субъекта (S) указывает кванторное слово.
«Все» – всегда указывает на распределенность субъекта,
«некоторые» - всегда указывает на нераспределенность субъекта
На распределенность предиката (Р) указывает логическая связь.
«Не есть» – указывает на распределенность предиката, в
суждениях со связкой «есть» распределенность предиката(P)
определяется по смыслу

24.

3. Сложные суждения:
структура, виды, истинностные
значения логических связок.

25.

Сложное суждение
- это суждения, составными частями которого являются
простые суждения
Выражаются сложными предложениями, имеющими две и более
грамматических основ или простыми предложениями,
осложненными второстепенными членами
Если завтра будет хорошая погода, то дети пойдут на
прогулку

26.

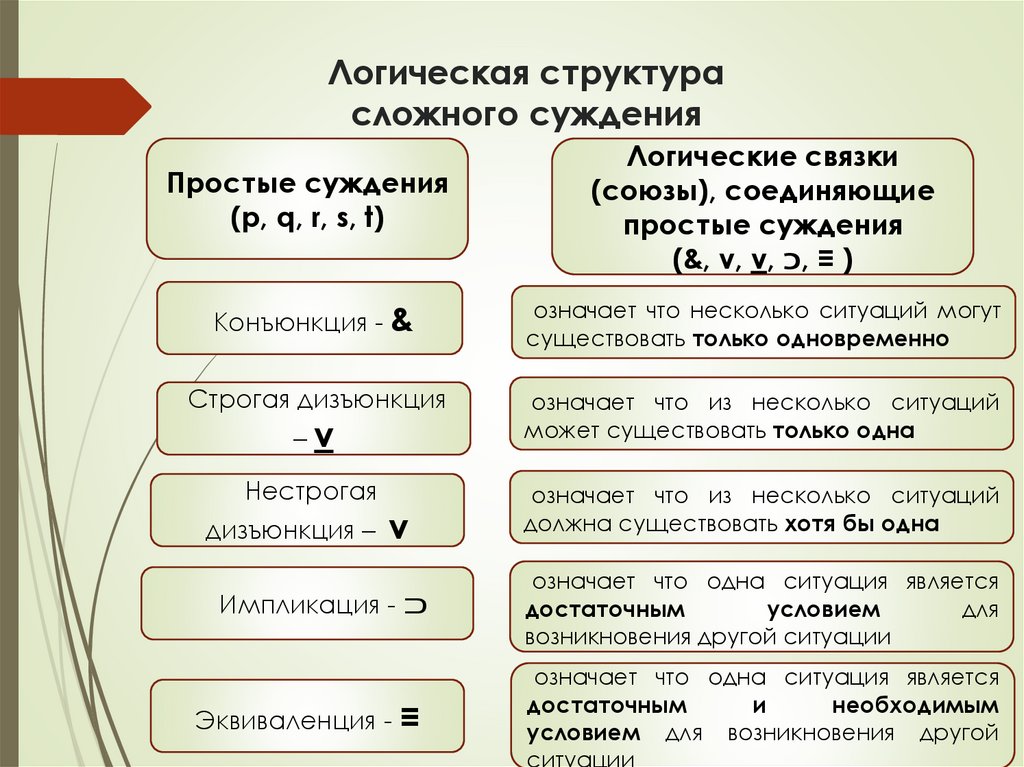
Логическая структура
сложного суждения
Простые суждения
(p, q, r, s, t)
Логические связки
(союзы), соединяющие
простые суждения
(&, v, v, ‫ ‬, ≡ )
Конъюнкция - &
означает что несколько ситуаций могут
существовать только одновременно
Строгая дизъюнкция
означает что из несколько ситуаций
может существовать только одна
Нестрогая
означает что из несколько ситуаций
должна существовать хотя бы одна
–v
дизъюнкция – v
Импликация - ⊃
означает что одна ситуация является
достаточным
условием
для
возникновения другой ситуации
Эквиваленция - ≡
означает что одна ситуация является
достаточным
и
необходимым
условием для возникновения другой
ситуации

27.

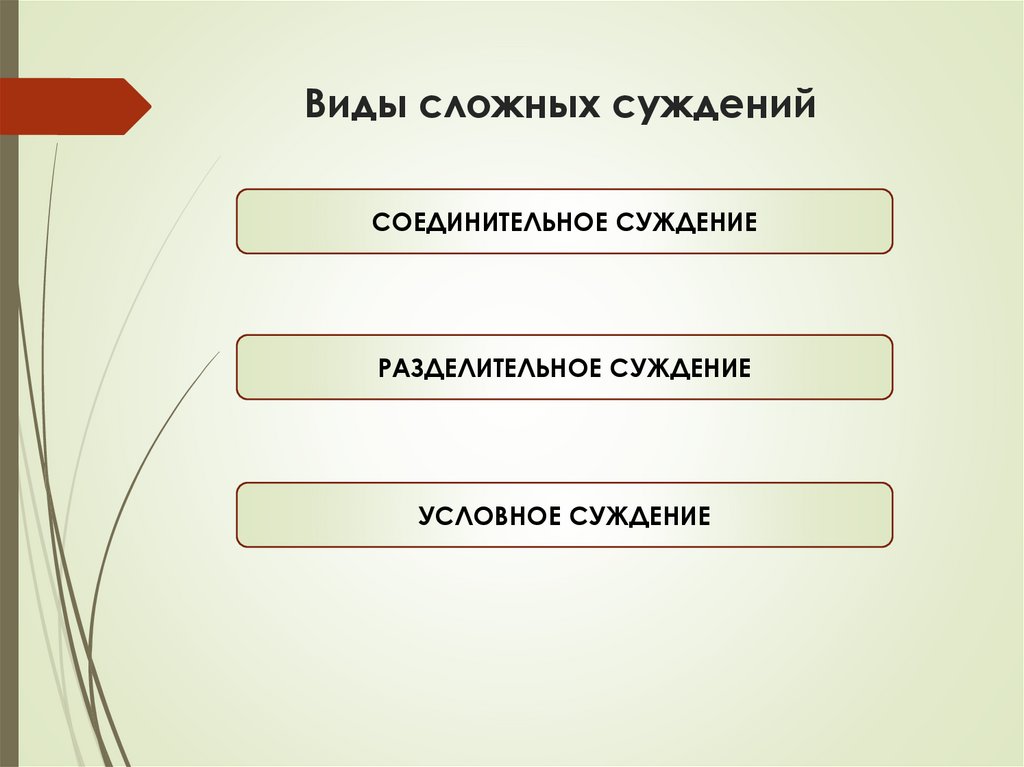
Виды сложных суждений
СОЕДИНИТЕЛЬНОЕ СУЖДЕНИЕ
РАЗДЕЛИТЕЛЬНОЕ СУЖДЕНИЕ
УСЛОВНОЕ СУЖДЕНИЕ

28.

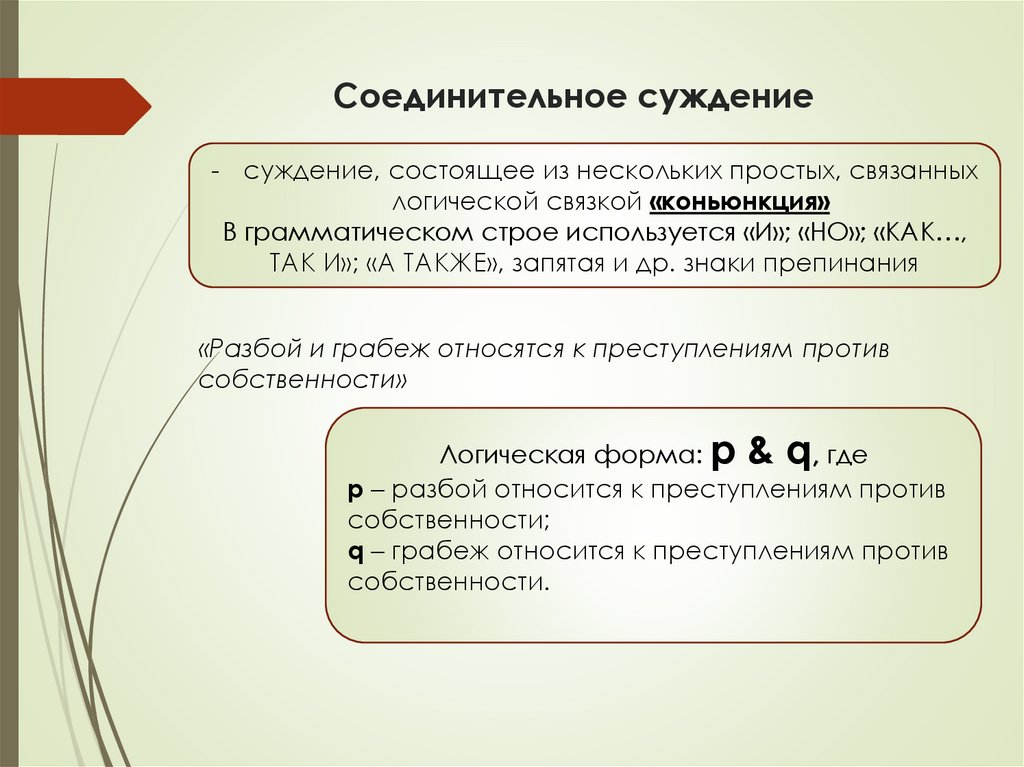
Соединительное суждение
- суждение, состоящее из нескольких простых, связанных
логической связкой «коньюнкция»
В грамматическом строе используется «И»; «НО»; «КАК…,
ТАК И»; «А ТАКЖЕ», запятая и др. знаки препинания
«Разбой и грабеж относятся к преступлениям против
собственности»
Логическая форма: p & q, где
р – разбой относится к преступлениям против
собственности;
q – грабеж относится к преступлениям против
собственности.

29.

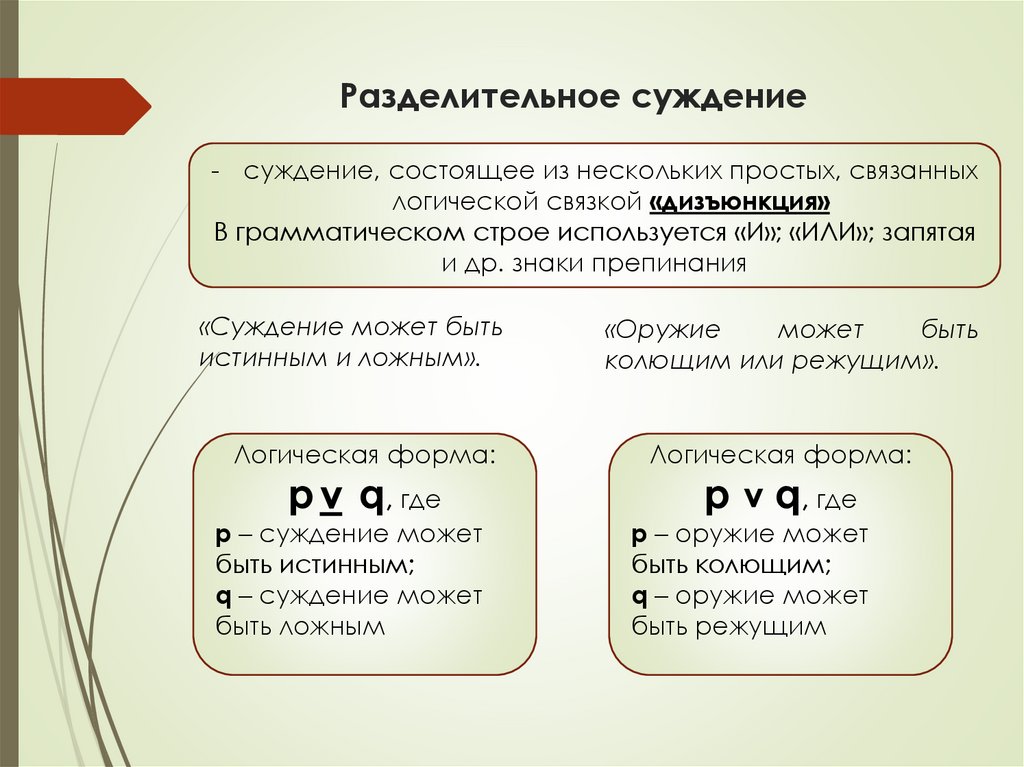
Разделительное суждение
- суждение, состоящее из нескольких простых, связанных
логической связкой «дизъюнкция»
В грамматическом строе используется «И»; «ИЛИ»; запятая
и др. знаки препинания
«Суждение может быть
истинным и ложным».
«Оружие
может
быть
колющим или режущим».
Логическая форма:
Логическая форма:
р – суждение может
быть истинным;
q – суждение может
быть ложным
р – оружие может
быть колющим;
q – оружие может
быть режущим
р v q, где
р v q, где

30.

Условное суждение
- суждение, состоящее из нескольких простых, связанных
логической связкой «импликация» или «эквиваленция»
В грамматическом строе используется или
подразумевается «Если.., то»
«Если преступление совершено
признается
совершенным
обстоятельствами».
группой
с
лиц, то оно
отягчающими
Логическая форма: p ⊃ q, где
р – преступление совершено группой лиц (основание суждения);
q – преступление признается совершенным с отягчающими
обстоятельствами (следствие суждения).
«Если человек совершил преступление, то он подлежит
уголовной ответственности»
Логическая форма: p ≡ q, где
р – человек совершил преступление(основание суждения);
q – он подлежит уголовной ответственности(следствие суждения).

31.

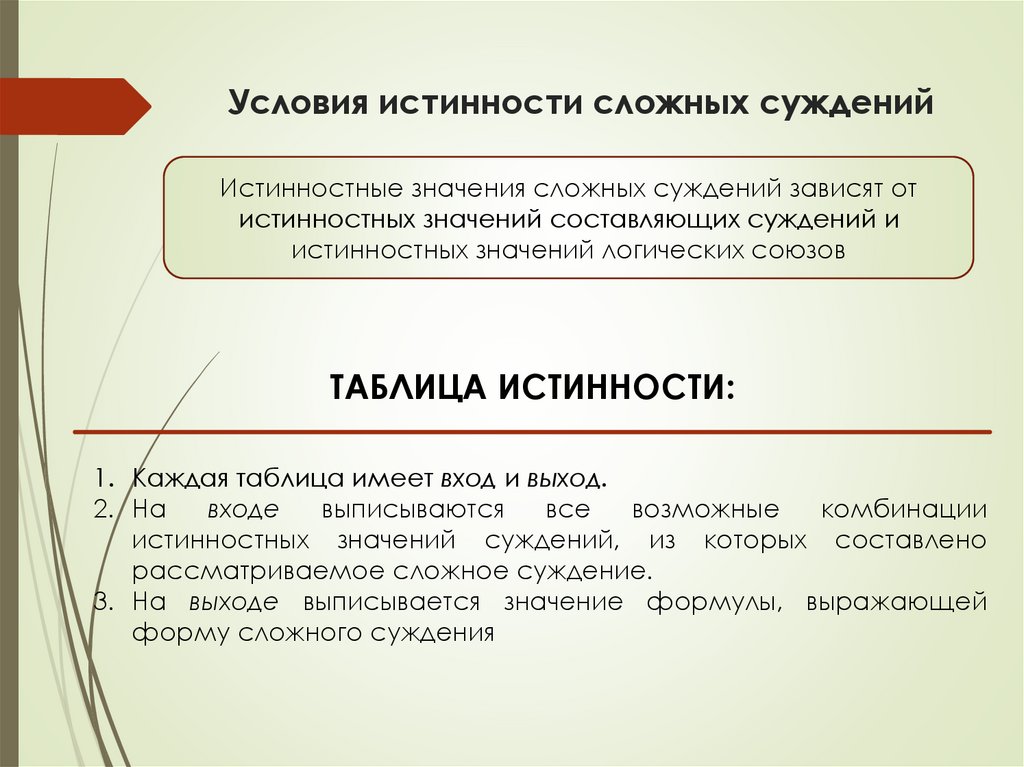
Условия истинности сложных суждений
Истинностные значения сложных суждений зависят от
истинностных значений составляющих суждений и
истинностных значений логических союзов
ТАБЛИЦА ИСТИННОСТИ:
1. Каждая таблица имеет вход и выход.
2. На
входе
выписываются
все
возможные
комбинации
истинностных значений суждений, из которых составлено
рассматриваемое сложное суждение.
3. На выходе выписывается значение формулы, выражающей
форму сложного суждения

32.

Сводная таблица истинности логических
союзов
p
q
p&q
pvq
pvq
p‫כ‬q
p≡q
И
И
И
И
Л
И
И
И
Л
Л
И
И
Л
Л
Л
И
Л
И
И
И
Л
Л
Л
Л
Л
Л
И
И
- Количество столбцов на входе зависит от количества
переменных;
- Количество строк вычисляется по формуле: x = 2n ,
Где х – число строк; n – количество переменных.

33.

Трактовка результатов таблицы истинности
- формула ТОЖДЕСТВЕННО ИСТИННАЯ – если она принимает
значение «И» во всех строках таблицы истинности, суждение в
этом случае признается ЛОГИЧЕСКИ НЕОБХОДИМЫМ
- формула ТОЖДЕСТВЕННО ЛОЖНАЯ – если она принимает
значение «Л» во всех строках таблицы истинности, суждение в
этом случае признается ЛОГИЧЕСКИ НЕВОЗМОЖНЫМ
- формула СОБСТВЕННО ВЫПОЛНИМАЯ – если она принимает
значение «И» и «Л» в строках таблицы истинности, суждение в
этом случае признается ЛОГИЧЕСКИ СЛУЧАЙНЫМ

34.

4. Отношения между суждениями.

35.

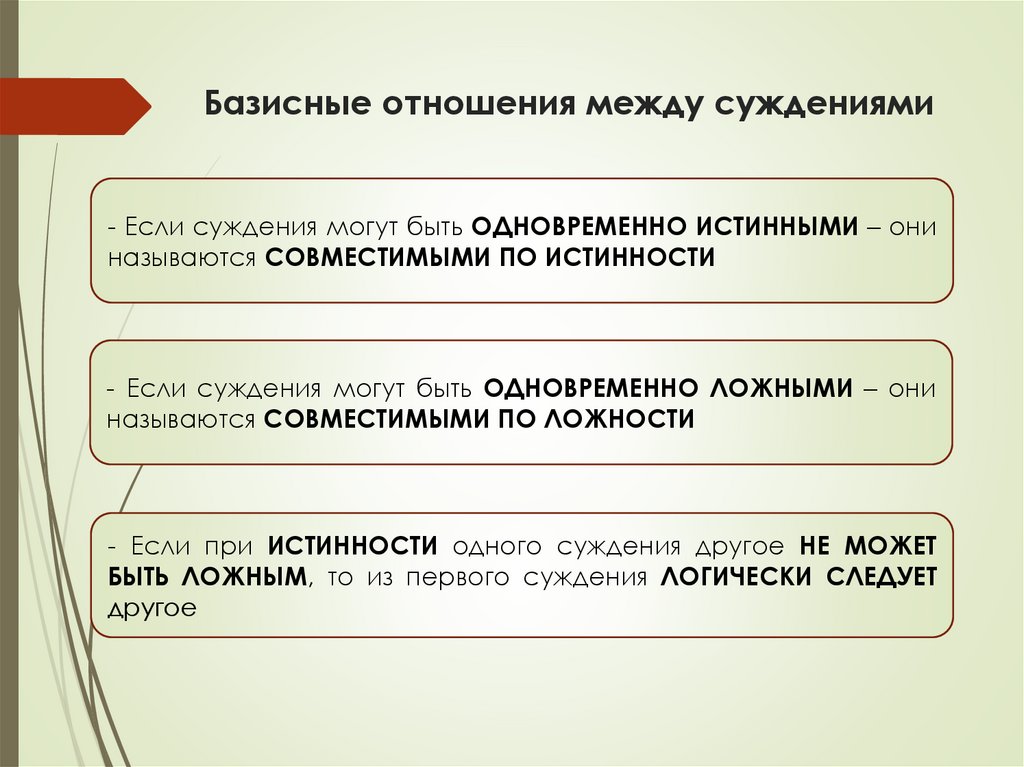
Базисные отношения между суждениями
- Если суждения могут быть ОДНОВРЕМЕННО ИСТИННЫМИ – они
называются СОВМЕСТИМЫМИ ПО ИСТИННОСТИ
- Если суждения могут быть ОДНОВРЕМЕННО ЛОЖНЫМИ – они
называются СОВМЕСТИМЫМИ ПО ЛОЖНОСТИ
- Если при ИСТИННОСТИ одного суждения другое НЕ МОЖЕТ
БЫТЬ ЛОЖНЫМ, то из первого суждения ЛОГИЧЕСКИ СЛЕДУЕТ
другое

36.

Отношения между суждениями
- Если суждения совместимы по И, совместимы по Л, из первого
суждения логически следует второе и наоборот, то отношения между
ними называют ЭКВИВАЛЕНТНОСТЬЮ
- Если суждения совместимы по И, совместимы по Л, из первого
суждения логически следует второе, но не наоборот, то второе
находится в отношении ПОДЧИНЕНИЯ к первому
- Если суждения совместимы по И, но не совместимы по Л, и нет
логического следования ни от первого ко второму, ни от второго к
первому, то отношения между ними называются ЧАСТИЧНОЙ
СОВМЕСТИМОСТЬЮ (субконтрарность)
- Если суждения не совместимы по И, не совместимы по Л, и нет
логического следования ни от первого ко второму, ни от второго к
первому, то отношения между ними называют ПРОТИВОРЕЧИЕМ
- Если суждения не совместимы по И, но совместимы по Л, и нет
логического следования ни от первого ко второму, ни от второго к
первому,
то
отношения
между
ними
называют
ПРОТИВОПОЛОЖНОСТЬЮ

37.

Отношения между простыми суждениями
P
Все S есть Р
А
Все S не есть Р
Е
Некоторые S есть Р
I
Некоторые S не есть Р
О
И
Л
ИИ
S
Л
S
P
Л
И
Л
И
S
P
Л
Л
И
И
А - E – нет совместимости по И, есть совместимость по Л, нет логического
следования – отношение противоположности
А - I; Е - О – есть совместимость по И, есть совместимость по Л, есть
логическое следование от первого ко второму – отношение подчинения
А - О; Е - I – нет совместимости по И, нет совместимости по Л, нет
логического следования – отношение противоречия
I - О – есть совместимость по И, нет совместимости по Л, нет логического
следование– отношение частичной совместимости

38.

ЛОГИЧЕСКИЙ КВАДРАТ
Все дети любят
мороженое
А
Противоположность
П
О
Д
Ч
И
Н
Е
Н
И
Е
Некоторые дети I
любят мороженое
Е
П
О
Д
Ч
И
Н
Е
Н
И
Е
Частичная
совместимость
Ни один ребенок не
любит мороженое
противоречие
O Некоторые дети не любят
мороженое

39.

ОТНОШЕНИЯ ПО ЛОГИЧЕСКОМУ КВАДРАТУ
А→I; E→O; ˥I→˥А; ˥О→˥Е;
Подчинение
Частичная
совместимость
˥I→O; ˥O→I
Противоположность
А→˥Е; Е→˥А
Противоречие
A→˥O;E→˥I; ˥A→O;˥E→I
А
И
Л
Е
Л
Л
I
И
И
О
Л
И
Л
И
Л
И

40.

5. Операция отрицания.

41.

ОТРИЦАНИЕ СУЖДЕНИЙ В ЛОГИКЕ
- это логическая операция, которая представляет собой такое
изменение логического содержания суждения, при котором его
значение меняется на противоположное.
Простое категорическое
суждение
Единичное суждение
Изменение количественной и
качественной характеристики
на противоположную
Изменение качественной
характеристики
на
противоположную
˥A O;
˥E I;
˥O A;
˥I E
˥A Е;
˥E А;

42.

ОТРИЦАНИЕ СЛОЖНЫХ СУЖДЕНИЙ
Законы де Моргана
˥(p & q) (˥p v ˥q);
˥(p v q) (˥p &˥q);
˥(p ‫ כ‬q) (p & ˥q);
˥(p ≡ q) ((˥p & q) v (p & ˥q));
˥ (p v q) (p ≡ q)