Геометрический смысл производной: k = tg α

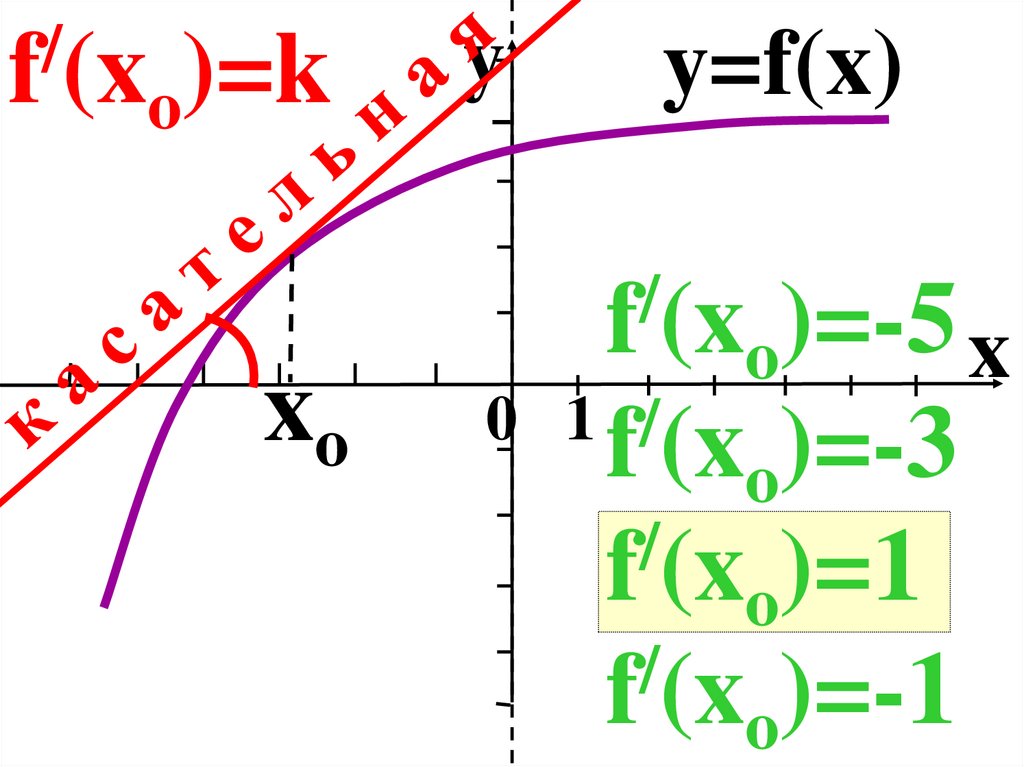
1.

/
f (xo)=k
xo
y
y=f(x)
/
f (xo)=-5 x
0 1 /
f (xo)=-3
/
f (xo)=1
/
f (xo)=-1

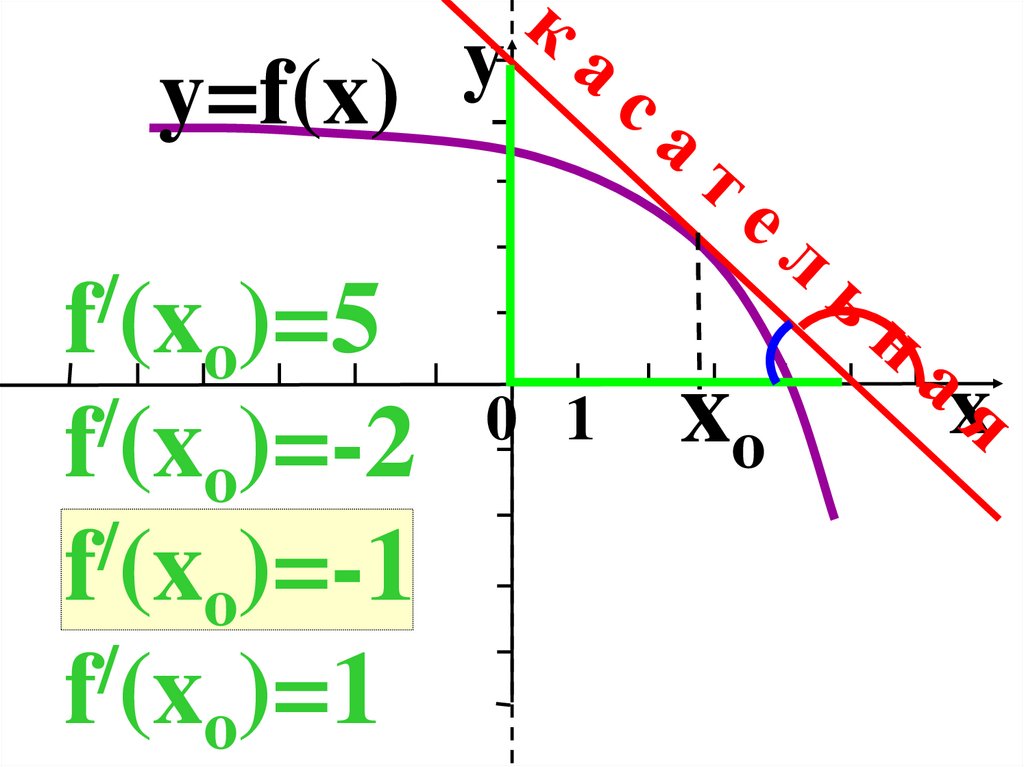
2.

y
/
f (xo)=k
k=tgα
/
f (xo)=-5
/
f (xo)=-3x
xo 0 1 f/(x )=1
o
/
f (xo)=2

3.

y
y=f(x)
/
f (xo)=5
/
f (xo)=-2
/
f (xo)=-1
/
f (xo)=1
0 1
xo
x

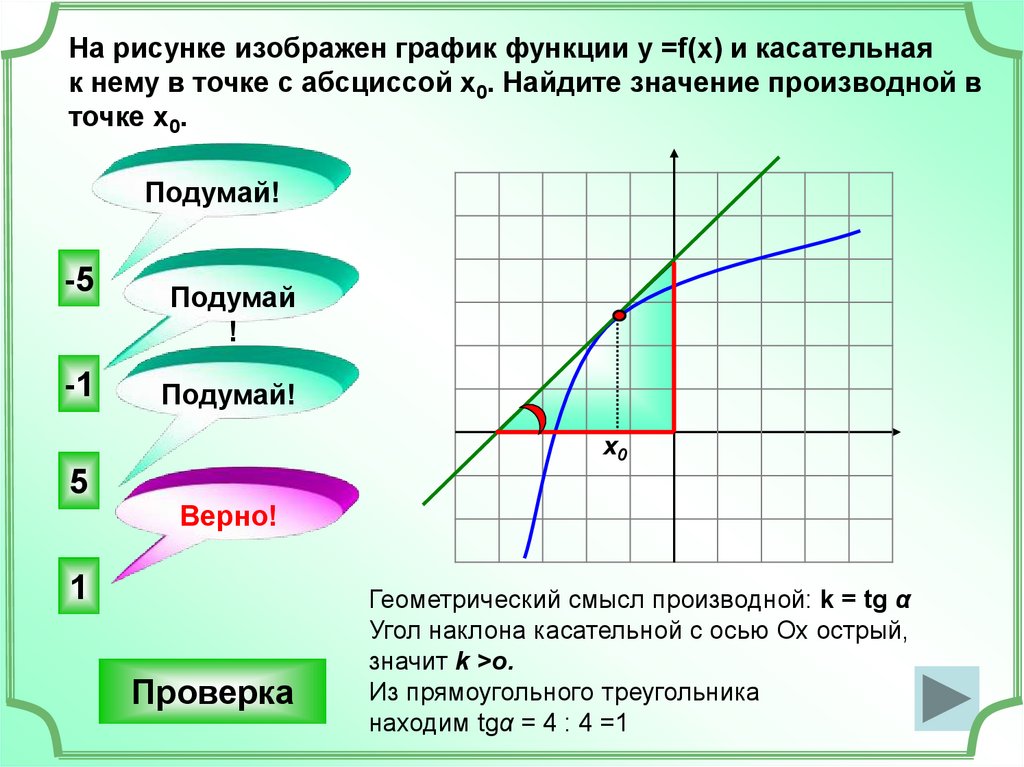
4.

На рисунке изображен график функции у =f(x) и касательная
к нему в точке с абсциссой х0. Найдите значение производной в
точке х0.
Подумай!
-5
-1
Подумай
!
Подумай!
х0
5
Верно!
1
Проверка
Геометрический смысл производной: k = tg α
Угол наклона касательной с осью Ох острый,
значит k >o.
Из прямоугольного треугольника
находим tgα = 4 : 4 =1

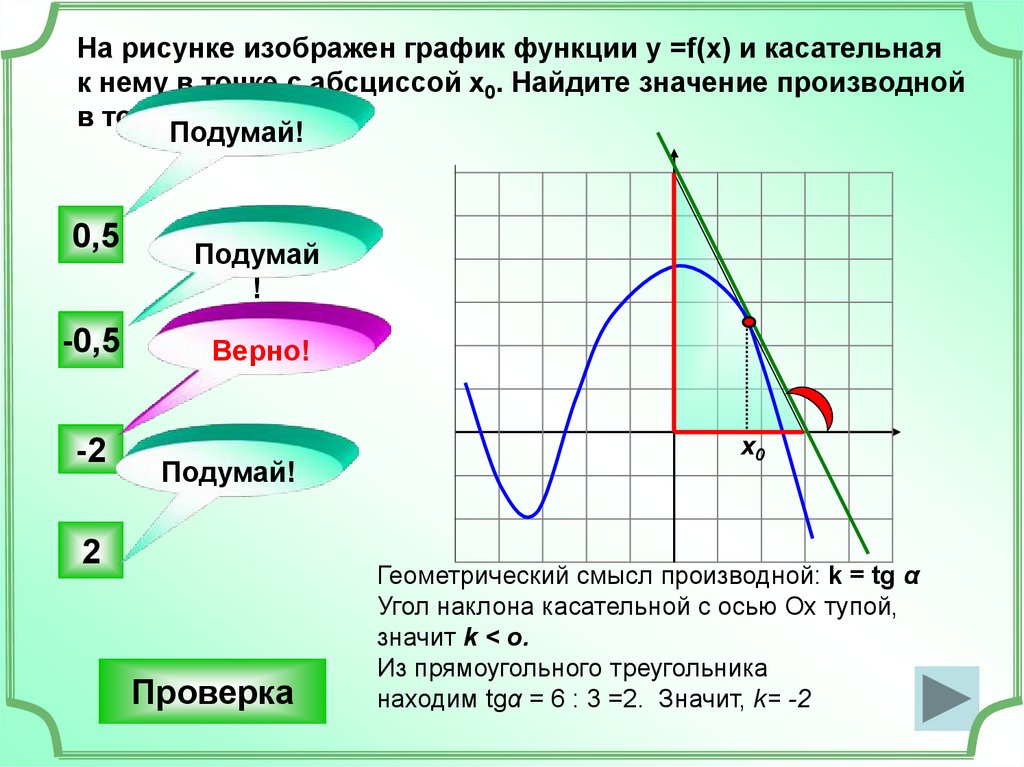
5.

На рисунке изображен график функции у =f(x) и касательная
к нему в точке с абсциссой х0. Найдите значение производной
в точке х0.
Подумай!
0,5
-0,5
-2
Подумай
!
Верно!
Подумай!
2
Проверка
х0
Геометрический смысл производной: k = tg α
Угол наклона касательной с осью Ох тупой,
значит k < o.
Из прямоугольного треугольника
находим tgα = 6 : 3 =2. Значит, k= -2

6.

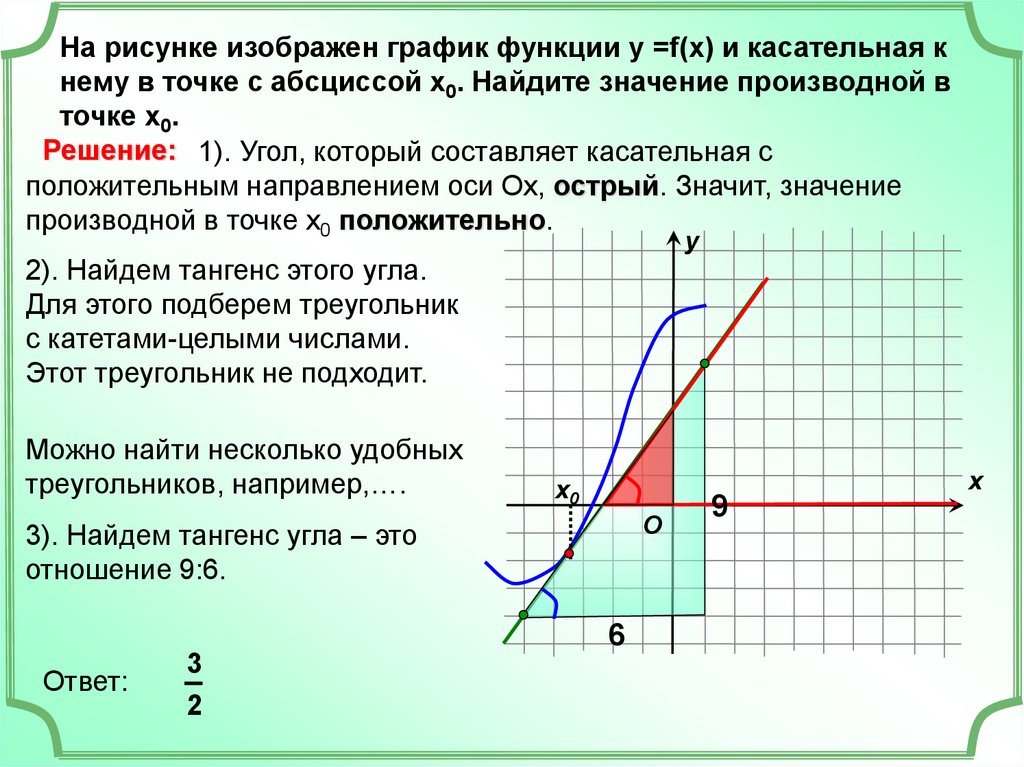
На рисунке изображен график функции у =f(x) и касательная к
нему в точке с абсциссой х0. Найдите значение производной в
точке х0.
Решение: 1). Угол, который составляет касательная с
положительным направлением оси Ох, острый. Значит, значение
производной в точке х0 положительно.
у
2). Найдем тангенс этого угла.
Для этого подберем треугольник
с катетами-целыми числами.
Этот треугольник не подходит.
Можно найти несколько удобных
треугольников, например,….
х0
O
3). Найдем тангенс угла – это
отношение 9:6.
6
Ответ:
3
2
9
х

7.

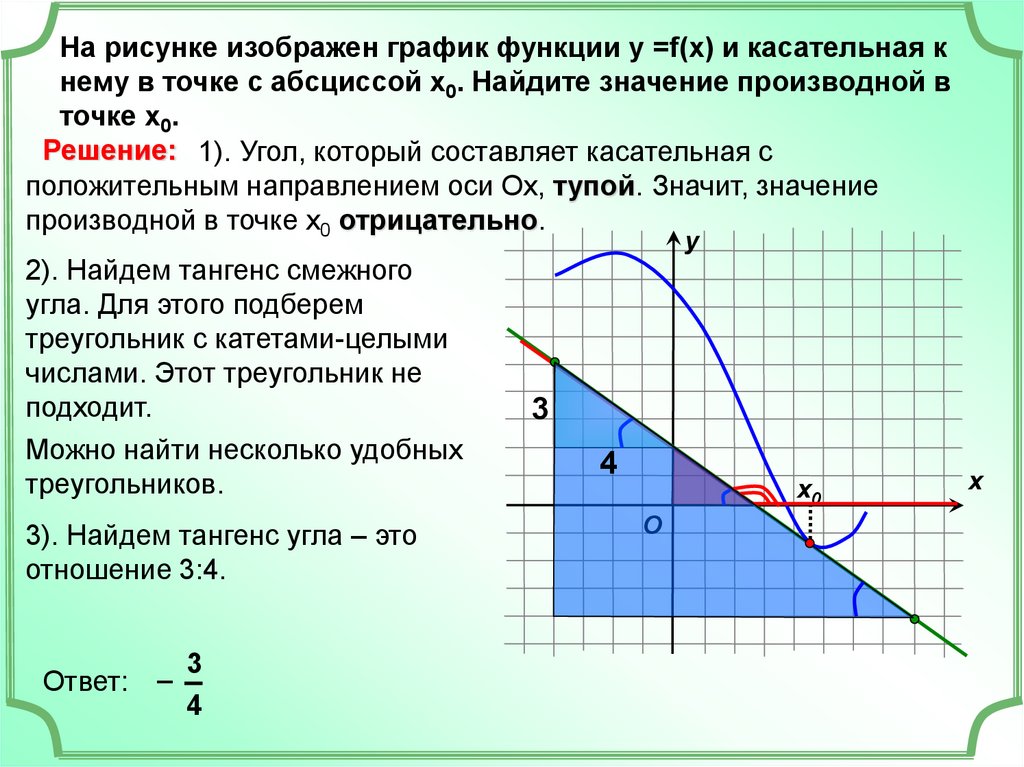
На рисунке изображен график функции у =f(x) и касательная к
нему в точке с абсциссой х0. Найдите значение производной в
точке х0.
Решение: 1). Угол, который составляет касательная с
положительным направлением оси Ох, тупой. Значит, значение
производной в точке х0 отрицательно.
2). Найдем тангенс смежного
угла. Для этого подберем
треугольник с катетами-целыми
числами. Этот треугольник не
подходит.
Можно найти несколько удобных
треугольников.
3). Найдем тангенс угла – это
отношение 3:4.
Ответ: –
3
4
у
3
4
х0
O
х

8.

На рисунке изображен график функции у =f(x) и касательная к
нему в точке с абсциссой х0. Найдите значение производной в
точке х0.
Решение: Решать подобные задания можно другим способом.
Уравнение прямой у = kx + b.
В этом уравнении угловой коэффициент k - искомая величина.
f/(xo)=k
у = kх + b
k=tgα
у
Подставим координаты известных
точек в уравнение прямой.
– 6 = 2k + b.
х
х0 O
–
– 4 = –2k + b.
– 2 = 4k
:4
(2; -6)
1
k=–
2
Ответ: –
(-2; -4)
1
2