Геометрический смысл производной

1.

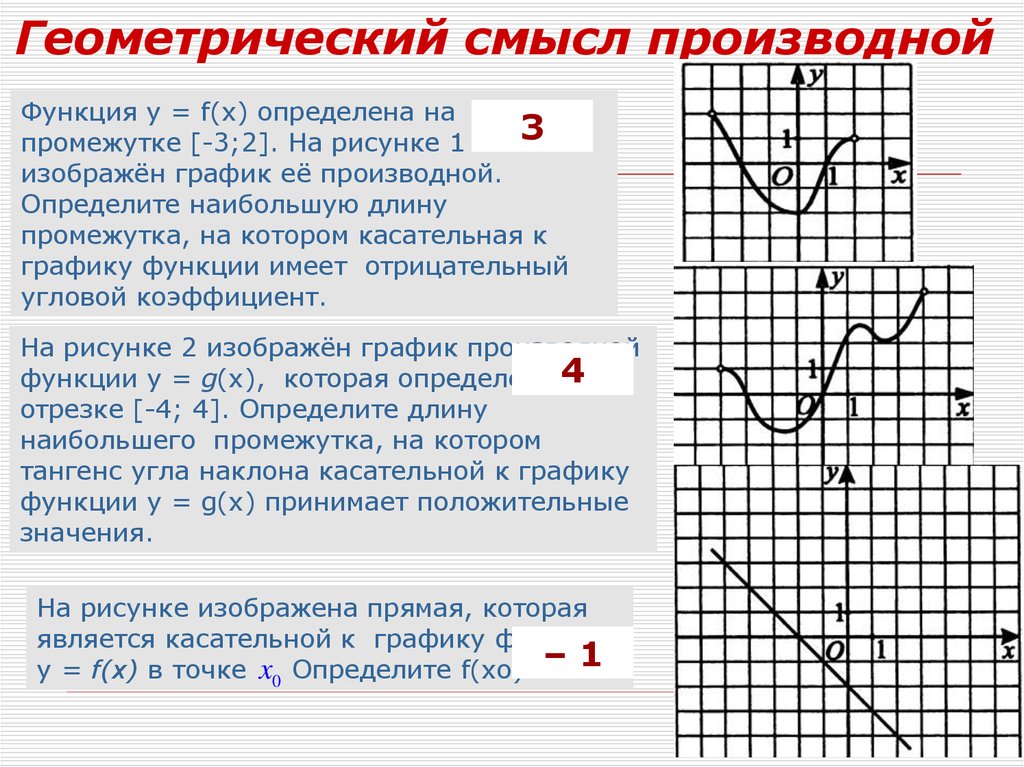
Геометрический смысл производной
Функция у = f(x) определена на
3
промежутке [-3;2]. На рисунке 1
изображён график её производной.
Определите наибольшую длину
промежутка, на котором касательная к
графику функции имеет отрицательный
угловой коэффициент.
На рисунке 2 изображён график производной
функции у = g(х), которая определена 4
на
отрезке [-4; 4]. Определите длину
наибольшего промежутка, на котором
тангенс угла наклона касательной к графику
функции у = g(x) принимает положительные
значения.
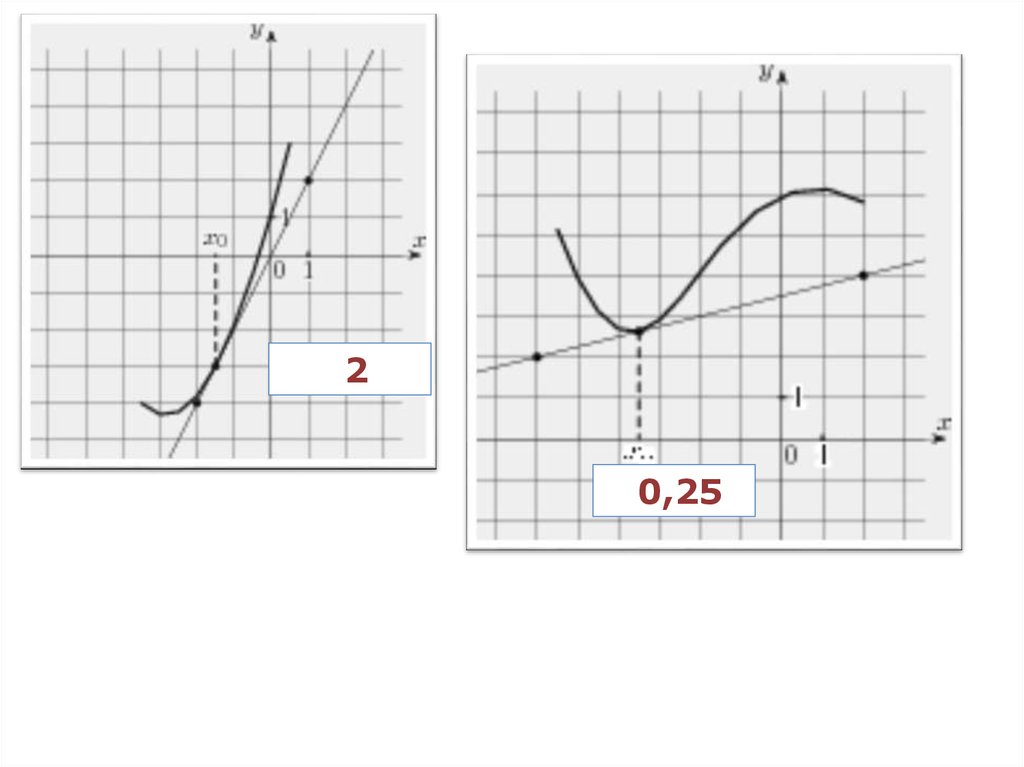
На рисунке изображена прямая, которая
является касательной к графику функции
у = f(x) в точке x0 Определите f(xo). – 1

2.

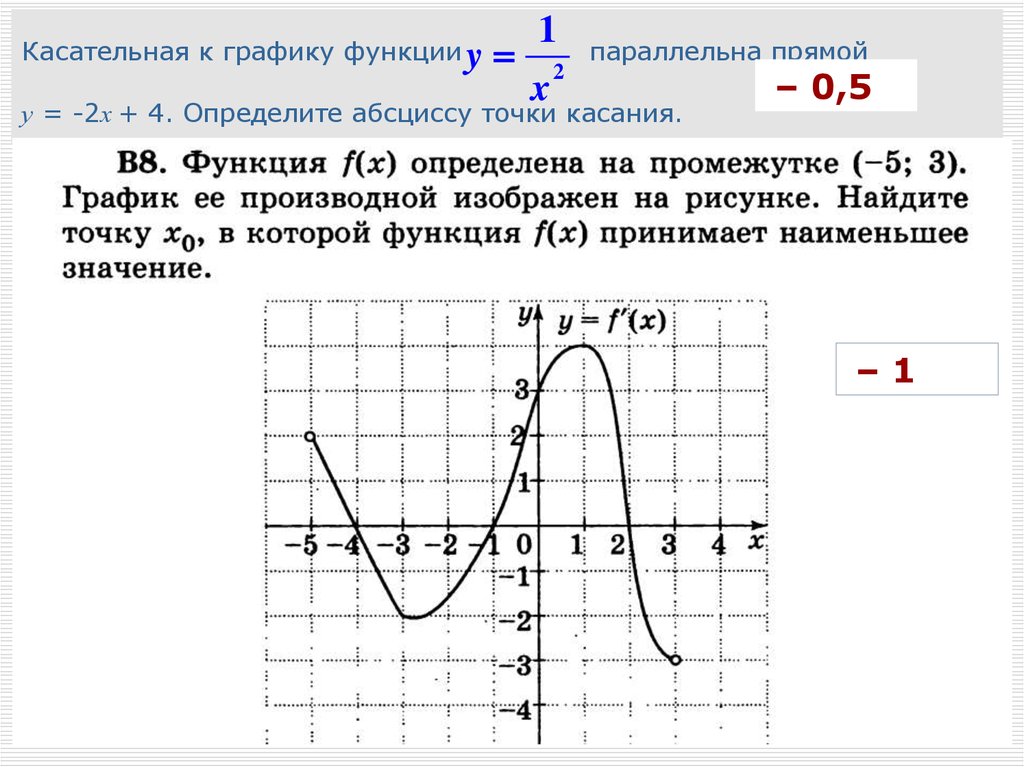
Касательная к графику функции y
1
x
2
параллельна прямой
у = -2х + 4. Определите абсциссу точки касания.
– 0,5
–1

3.

–5

4.

5
2

5.

4
4
3

6.

3
2

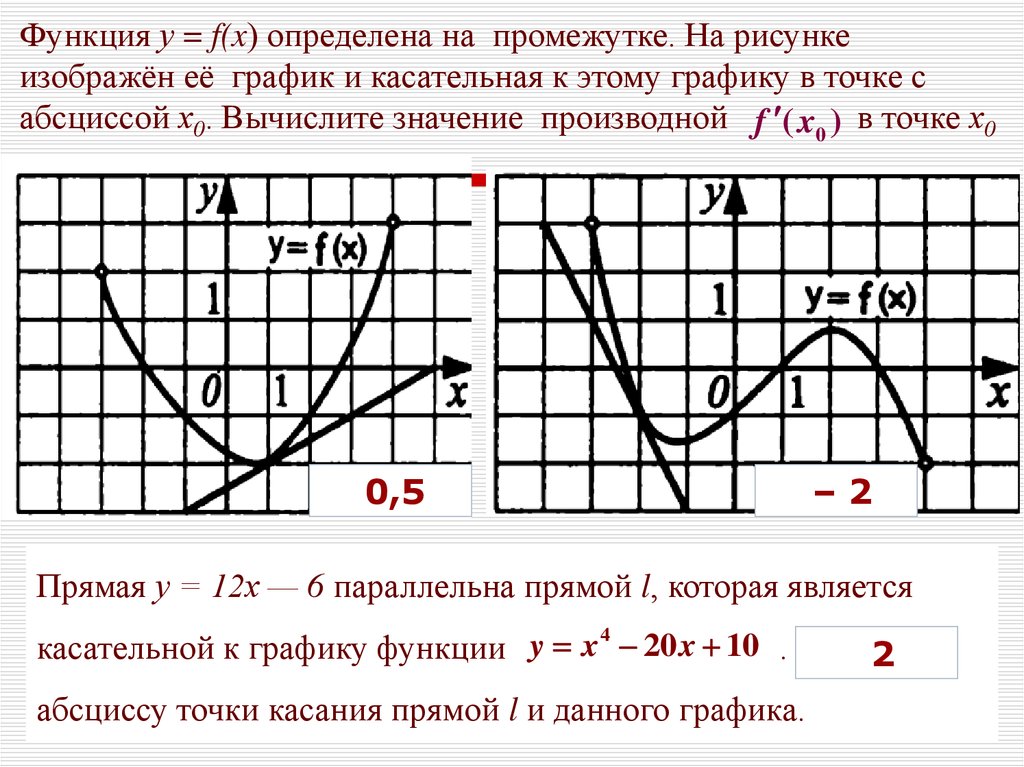
7.

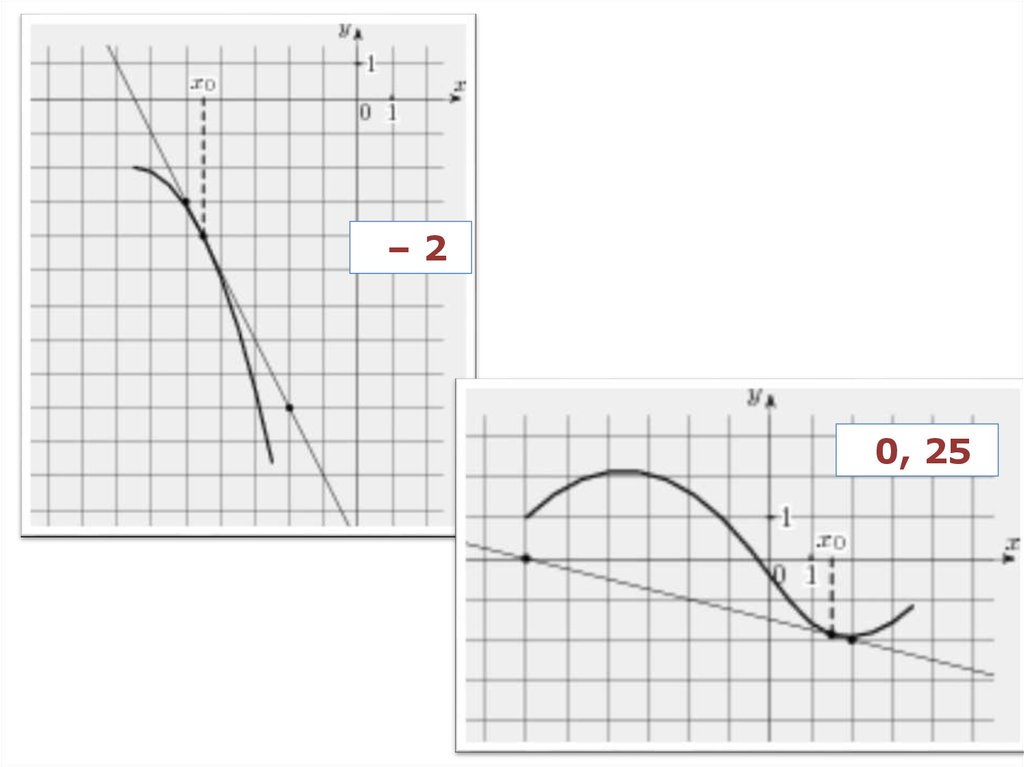
Функция у = f(x) определена на промежутке. На рисунке
изображён её график и касательная к этому графику в точке с
абсциссой х0. Вычислите значение производной f ( x0 ) в точке х0
0,5
–2
Прямая у = 12х — 6 параллельна прямой l, которая является
4
касательной к графику функции y x 20 x 10 . Найдите
2
абсциссу точки касания прямой l и данного графика.

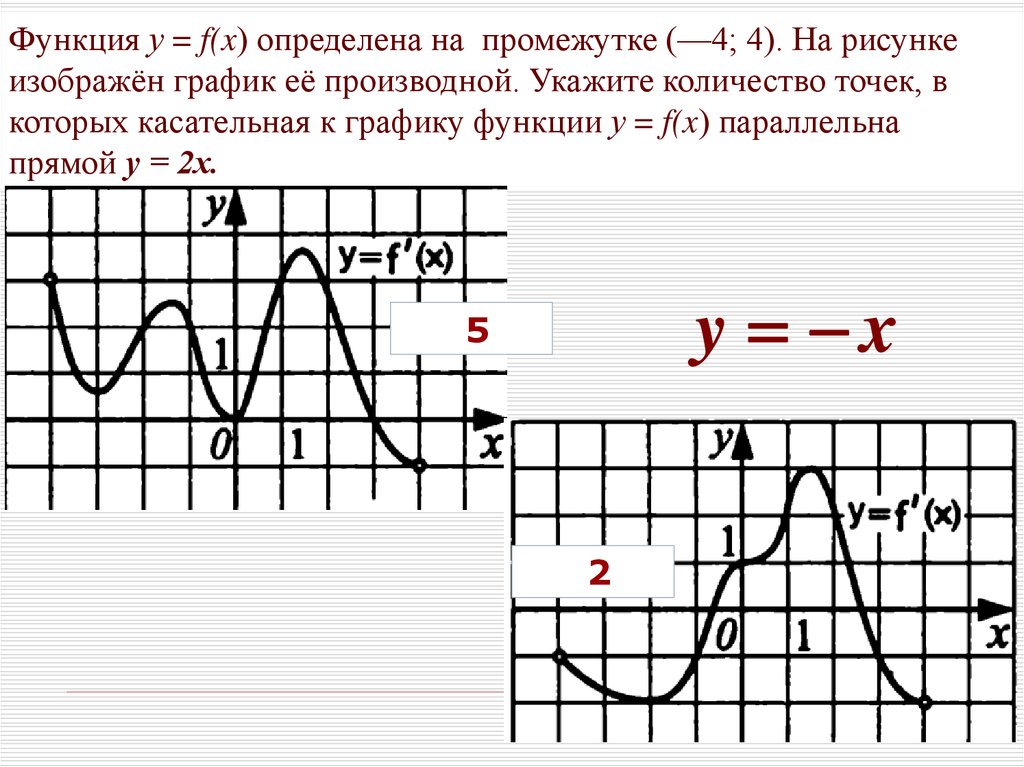
8.

Функция у = f(x) определена на промежутке (—4; 4). На рисунке
изображён график её производной. Укажите количество точек, в
которых касательная к графику функции у = f(x) параллельна
прямой у = 2х.
y x
5
2

9.

3
2

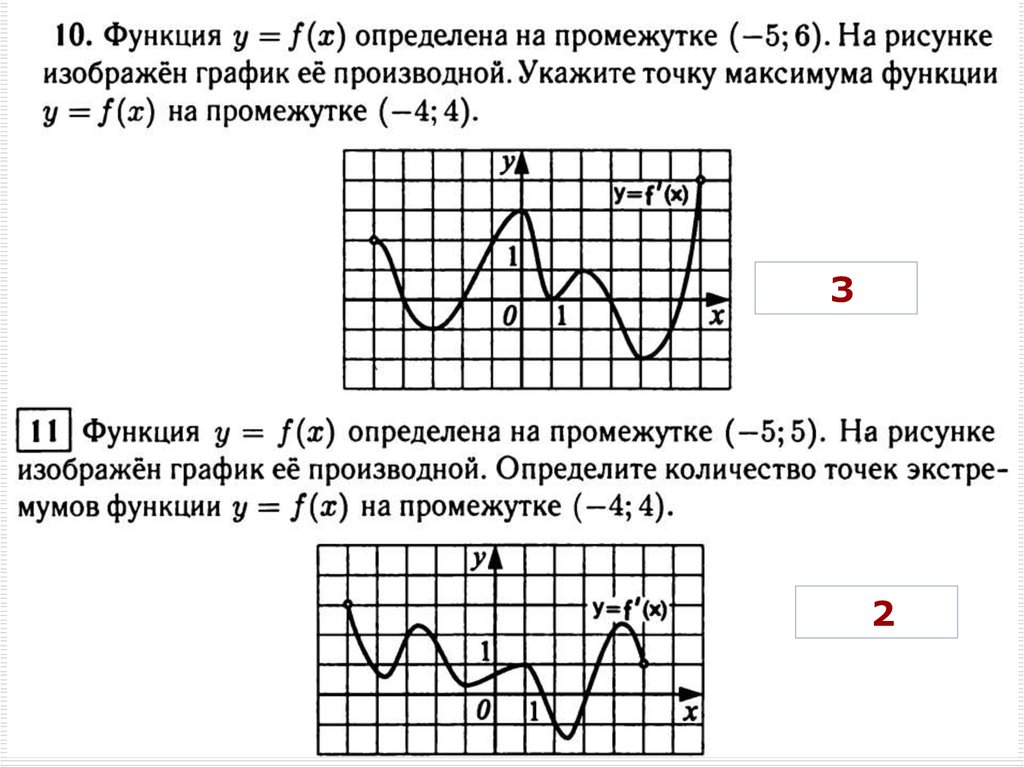
10.

6
4

11.

2
0,25

12.

–2
0, 25

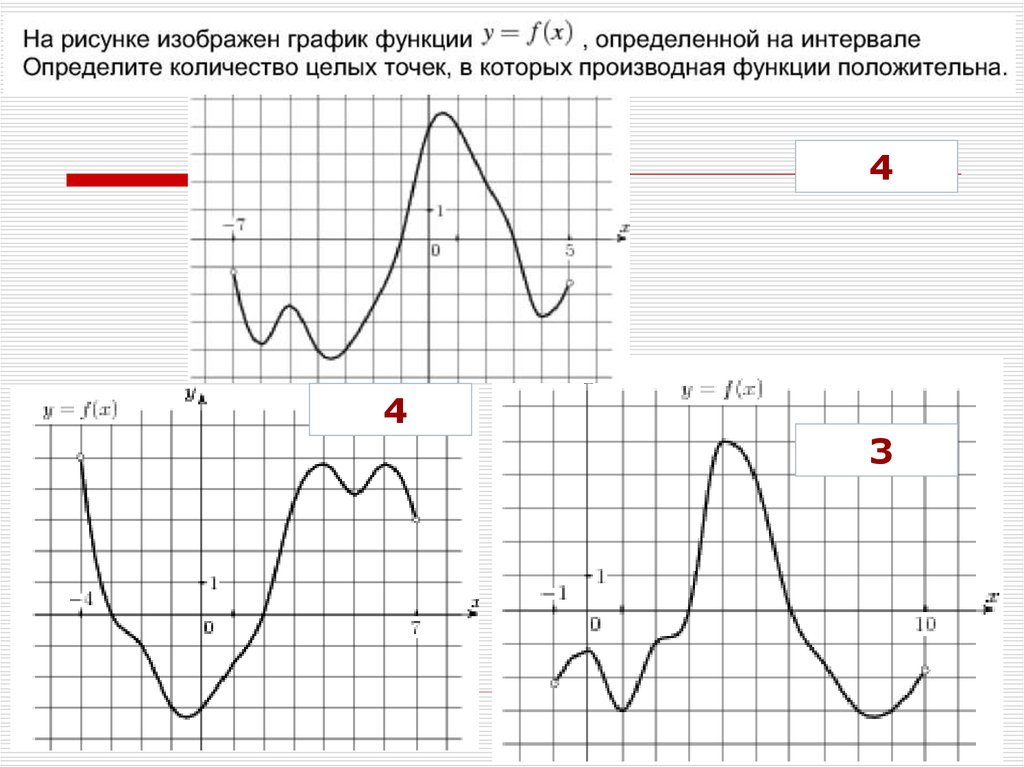
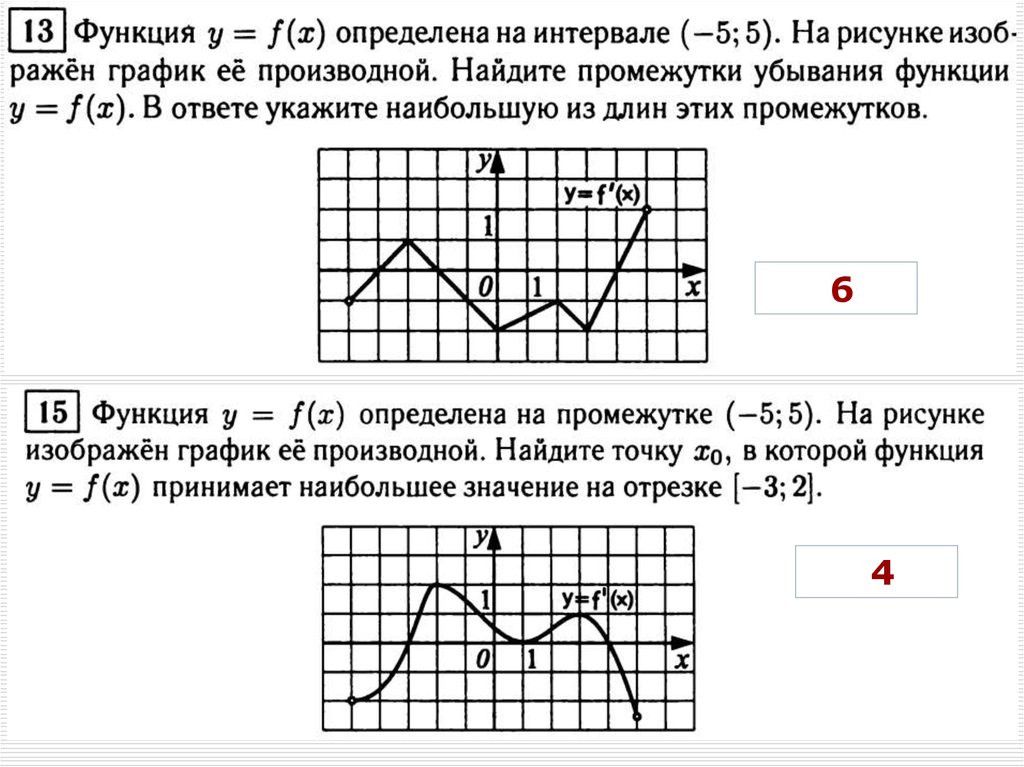
13.

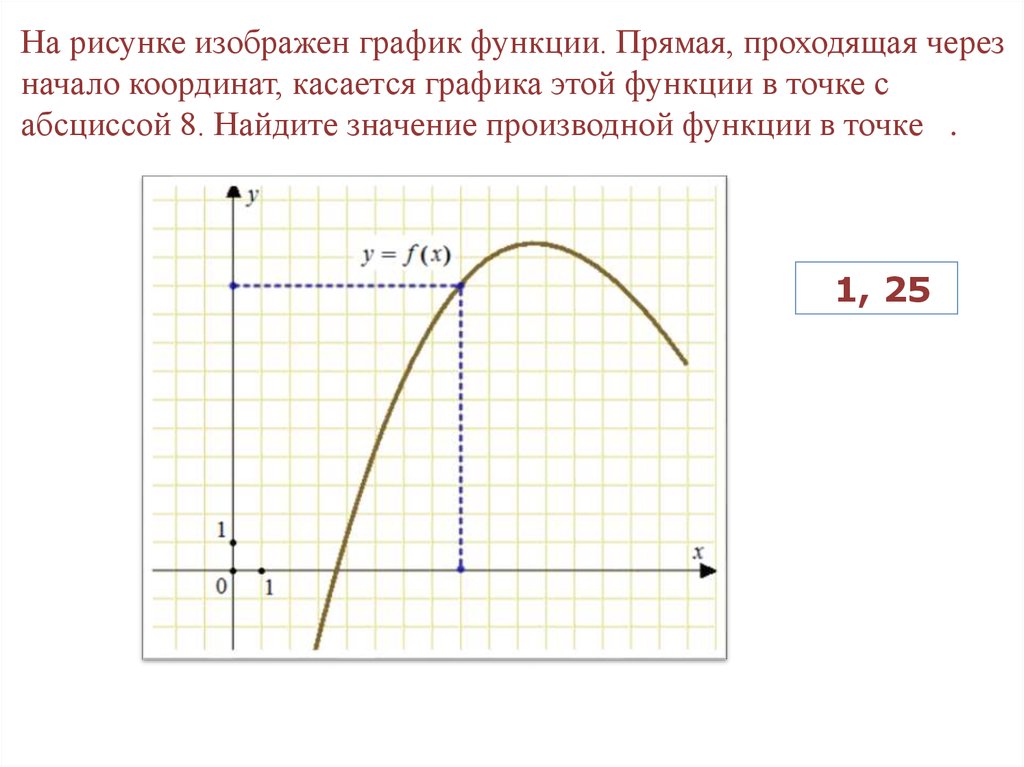
На рисунке изображен график функции. Прямая, проходящая через
начало координат, касается графика этой функции в точке с
абсциссой 8. Найдите значение производной функции в точке .
1, 25

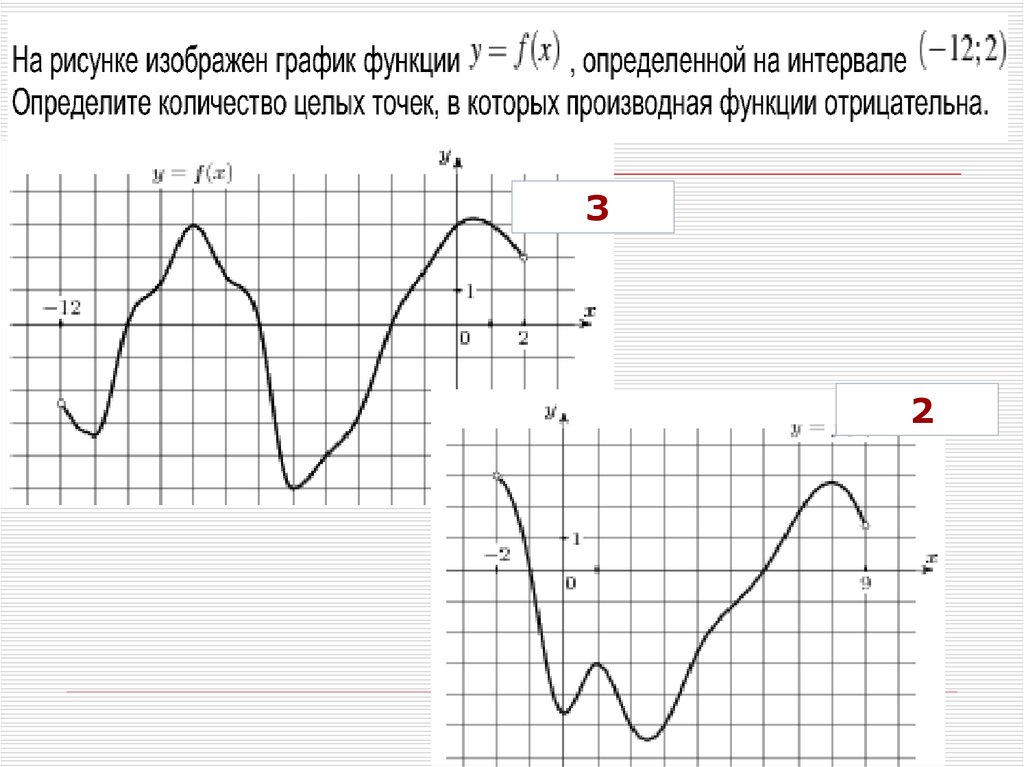
14.

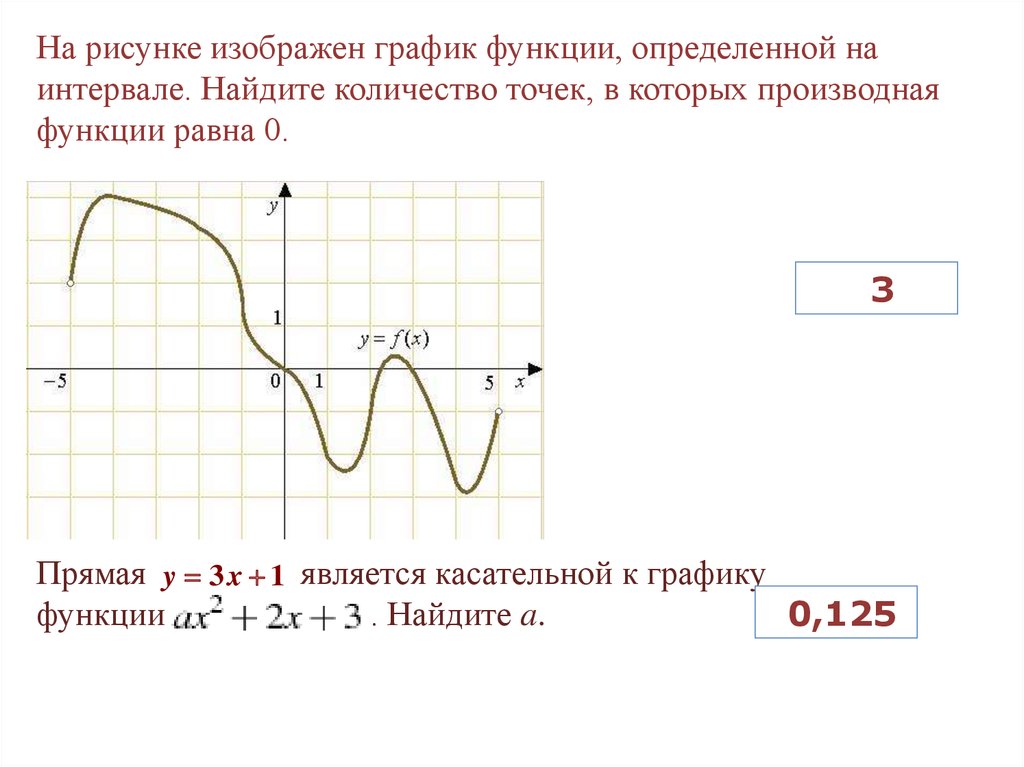
На рисунке изображен график функции, определенной на
интервале. Найдите количество точек, в которых производная
функции равна 0.
3
Прямая y 3 x 1 является касательной к графику
функции
. Найдите a.
0,125