Похожие презентации:
Монотонность и экстремумы функции
1.
Тема 3/1. Монотонность и экстремумыфункции.
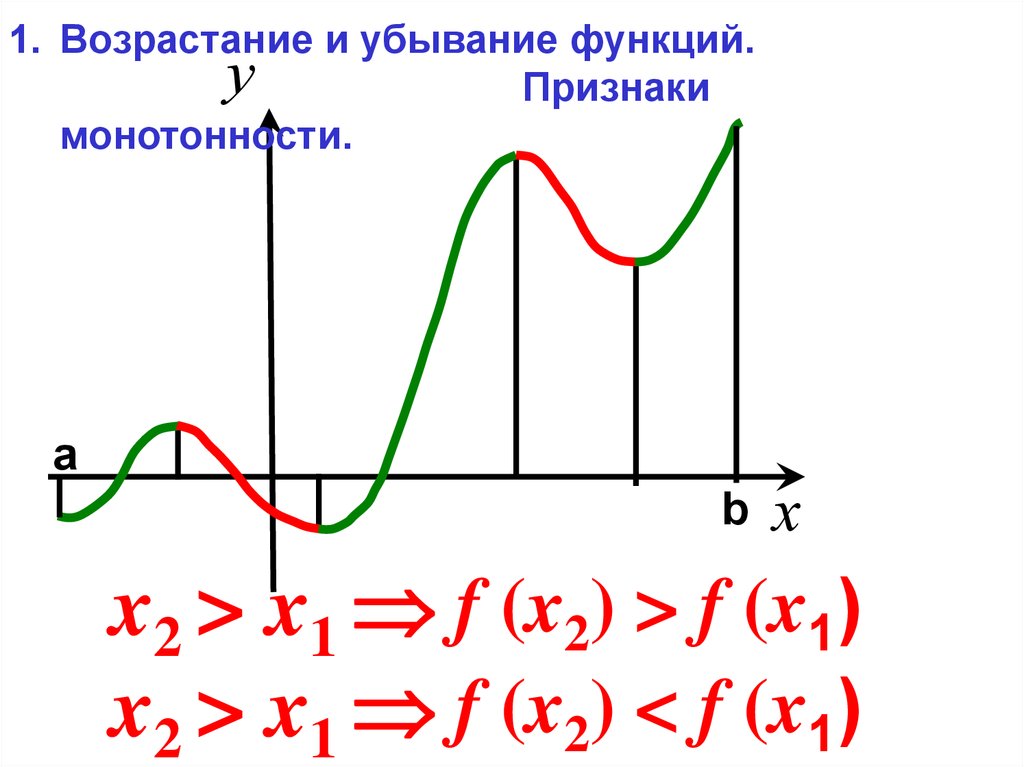
1. Возрастание и убывание функций. Признаки
монотонности.
2. Точки экстремума. Необходимое условие
экстремумов.
3. Достаточное условие экстремума.
2.
1. Возрастание и убывание функций.y
Признаки
монотонности.
a
b
x
x2 > x1 f (x2) > f (x1)
x2 > x1 f (x2) < f (x1)
3.
Признак возрастания функции.Для того, чтобы функция y=f(x) возрастала на промежутке, необходимо и достаточно, чтобы производная функции была
положительной на этом промежутке.
f (x)
<=> f (x) > 0
Признак убывания функции.
Для того , чтобы функция y=f(x) убывала
на промежутке, необходимо и достаточно,
чтобы производная функции была отрицательной на этом промежутке.
f (x)
<=> f (x) < 0
4.
2. Точки экстремума. Необходимое условие экстремумовОпределение. Точка х0 называется точкой максимума(max),
если в некоторой окрестности точки х0 выполняется
неравенство
y
f (x0) > f (x) .
f ( x 0)
f (x)
x
x0
x
x0 - точка максимума,
f (x0) - максимум
5.
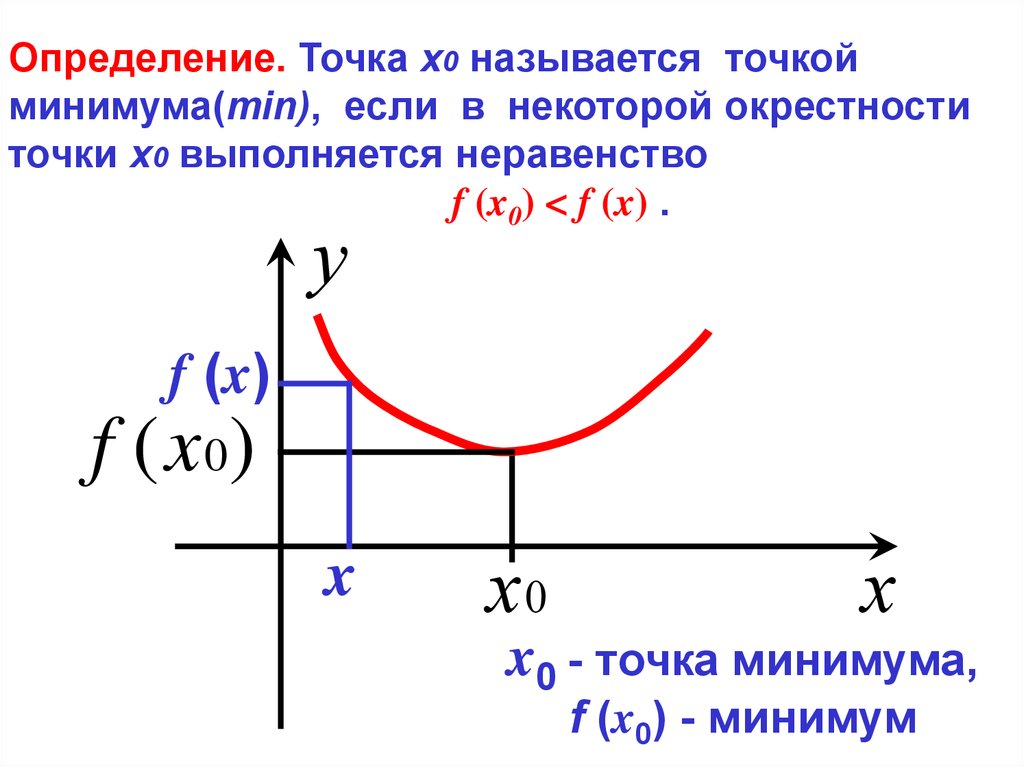
Определение. Точка х0 называется точкойминимума(min), если в некоторой окрестности
точки х0 выполняется неравенство
f (x0) < f (x) .
y
f (x)
f ( x 0)
x
x0
x
x0 - точка минимума,
f (x0) - минимум
6.
ya
x2
x1
x3
x4
b
x
7.
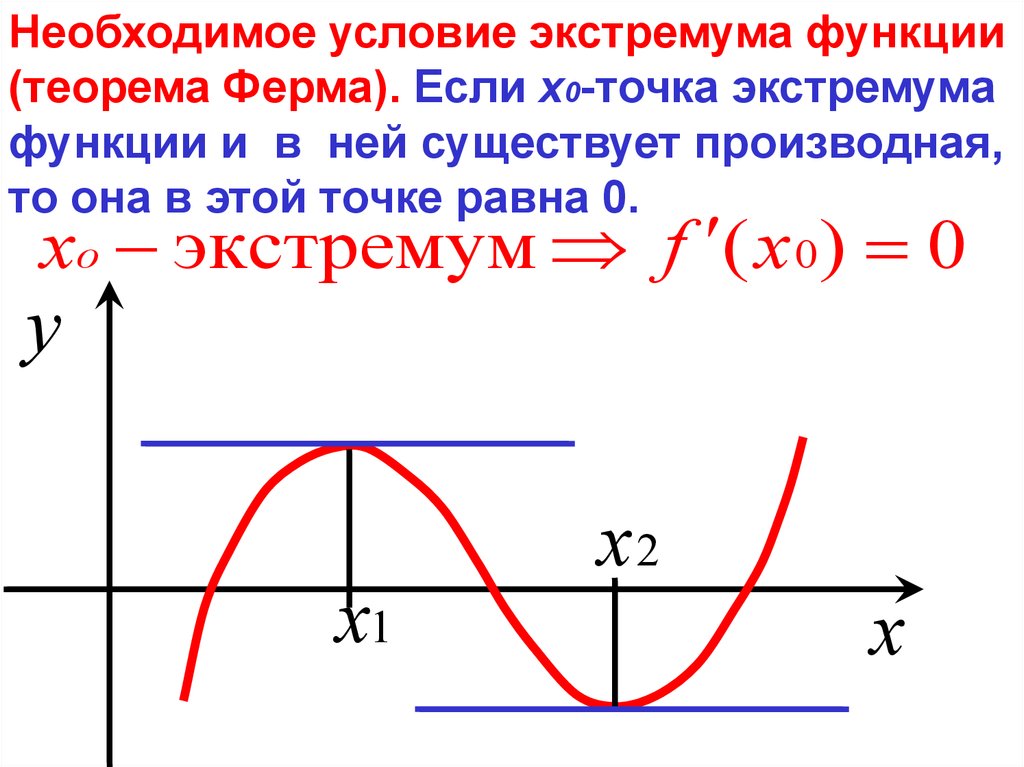
Необходимое условие экстремума функции(теорема Ферма). Если х0-точка экстремума
функции и в ней существует производная,
то она в этой точке равна 0.
xo экстремум f ( x 0) 0
y
x1
x2
x
8.
yy
x
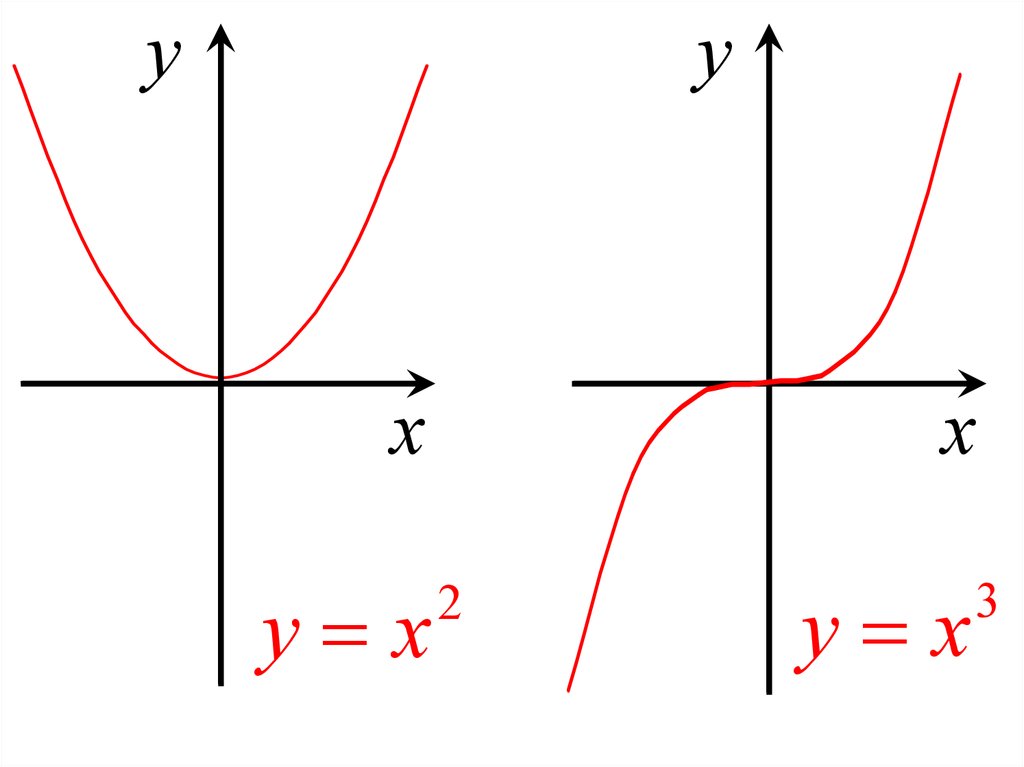
y x
x
2
y x
3
9.
3. Достаточное условие экстремума функции.Теорема (1-е достаточное условие
существования экстремума).
Пусть x0 - критическая точка функции
y=f(x) (т.е. f
( x 0) 0или не существует).
Если производная при переходе
через х0 меняет знак , то х0 является
точкой экстремума.
f
f
-
x0
+
,
то х0 – т. max
,
то х0 – т. min
+ x0
10.
Схема исследования функции намонотонность и экстремумы.
1. Найти f (x )
2. Найти критические точки 1-го рода.
(т.е. решить уравнение f (x) = 0 )
3. Установить знаки производной при
переходе через критические точки и
определить точки экстремума.
4. Найти значения функции в точках
экстремума.
11.
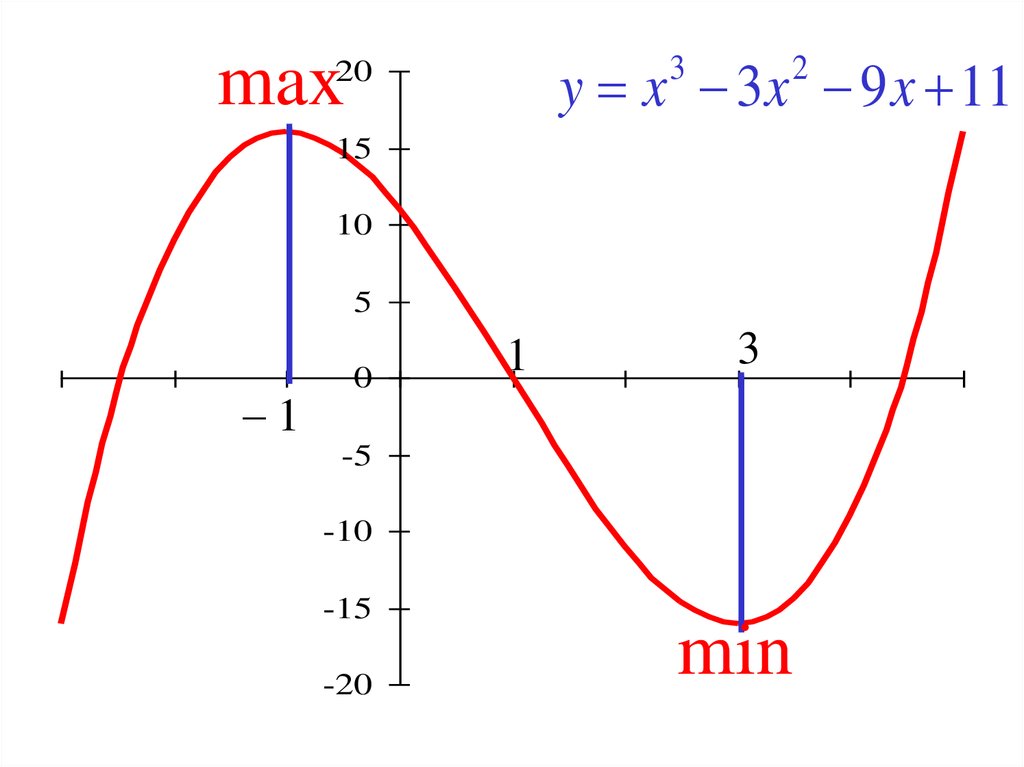
Пример. Исследовать функциюy x 3x 9 x 11
3
2
на монотонность, точки экстремума.
x
y'
y
( ; 1) -1 ( 1 ; 3)
+
0
Max
16
-
3 (3 ; )
0
Min
-16
+
12.
y x 3x 9 x 11max
3
20
2
15
10
5
1
0
1
3
-5
-10
-15
-20
min
13.
Исследование на экстремум спомощью производных высших
порядков.
14.
Теорема (2-е достаточное условиесуществования экстремума).
Пусть x0 - критическая точка функции,
т.е. f ( x 0) 0 или не существует.
Если вторая производная функции в
точке х0 положительна , то х0 - точка
минимума.
f ( x0 ) 0 x т. min
0
Если вторая производная функции в
точке x0 отрицательна, то x0 - точка
максимума.
f ( x0 ) 0 x т. max
0
15.
Пример Функцию y x 3 x 9 x 11исследовать на точки экстремума по
2-му достаточному условию.
3
2
1) y 0 x1 3 x 2 1
16.
Задание на самоподготовку:Дана функция
y x 12 x 4
3
1) исследовать функцию на
монотонность и экстремумы (2-мя
способами)











 Математика
Математика








