5.4 Монотонность функции и экстремумы. Примеры

1.

Применение производной для
исследования функции на
монотонность и экстремумы.

2.

Если производная дифференцируемой
функции положительна внутри
некоторого промежутка Х, то функция
возрастает на этом промежутке.

3.

Если производная дифференцируемой
функции отрицательна внутри
некоторого промежутка Х, то она
убывает на этом промежутке.

4.

Найти интервалы монотонности
функции
y x 4x 3
2

5.

Найдем производную этой функции:
y ( x2 4 x 3) 2 x 4
Исследуем знак этой производной:
y 0
2x 4 0 x 2
Расставляем знаки производной:
знак y
возрастает или убывает функция y
2
Следовательно,
функция будет возрастать на промежутке (2 ; )
функция будет убывать на промежутке
( ; 2)

6.

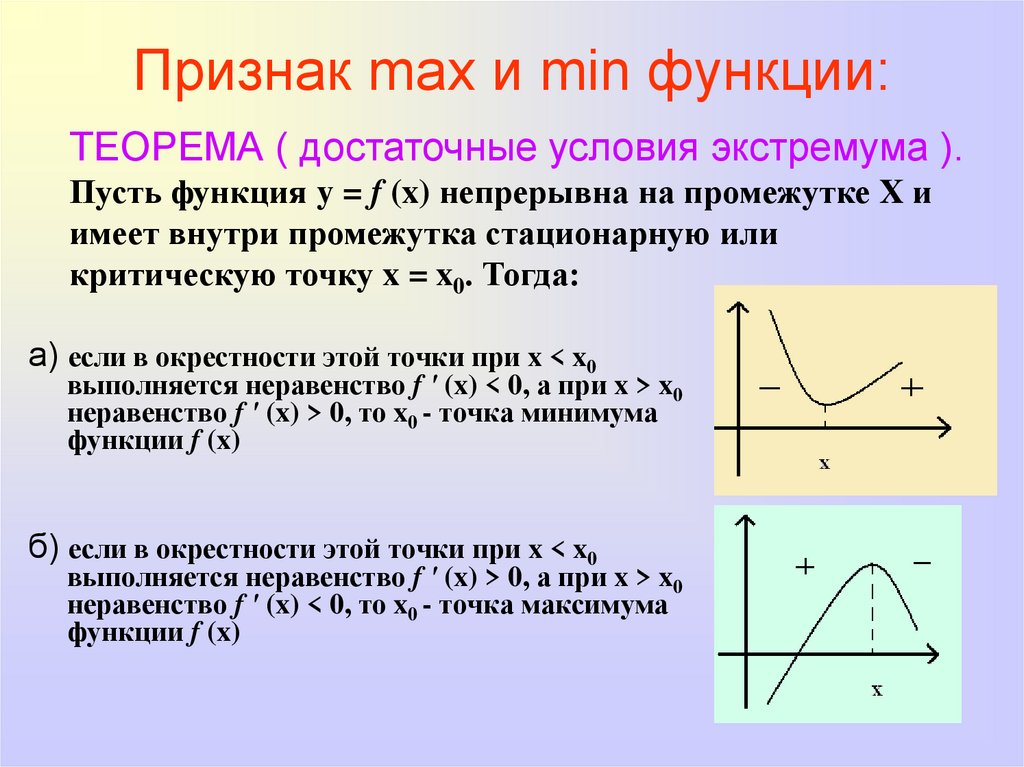
Признак max и min функции:
ТЕОРЕМА ( достаточные условия экстремума ).
Пусть функция y = f (x) непрерывна на промежутке X и
имеет внутри промежутка стационарную или
критическую точку x = x0. Тогда:
а) если в окрестности этой точки при x < x0
выполняется неравенство f ' (x) < 0, а при x > x0
неравенство f ' (x) > 0, то x0 - точка минимума
функции f (x)
б) если в окрестности этой точки при x < x0
выполняется неравенство f ' (x) > 0, а при x > x0
неравенство f ' (x) < 0, то x0 - точка максимума
функции f (x)

7.

Найдите промежутки возрастания и убывания функции,
точки экстремума и экстремумы
D(f)=R
f ' (x) = x2-5x+6
f ' (x) = 0 x2 - 5x + 6 = 0
x1=2 x2=3
x3 5 2
f ( x)
x 6x 1
3 2
знак y
возрастает или убывает функция y
f (x) возрастает на (-∞;2], [3;+∞)
f (x) убывает на [2;3]
2
max
Хmax=2
3
min
Xmin=3

8.

Алгоритм исследования непрерывной
функции y=f(x) на монотонность и
экстремумы
Найти область определения функции D(f).
Найти производную функции f ' (x).
Найти стационарные и критические точки.
Решить неравенства f ' (x) > 0 и f ' (x) < 0
методом интервалов.
5. Сделать вывод о монотонности функции и о
её точках экстремума.
1.
2.
3.
4.

9.

Найдите промежутки возрастания и убывания и точки
экстремума функции f(x)= - 5x5 + 3x3.
D(f)=R
f ' (x) = - 25x4 + 9x2 = x2(-25x2+9)
f ' (x) = 0
x2(-25x2+9)=0
x=0
x=±3/5
знак y
возрастает или убывает функция y
-3/5
f (x) возрастает на [-3/5;3/5]
f (x) убывает на (-∞;-3/5], [3/5;+∞)
Xmax=3/5
Xmin=-3/5
0
3/5

10.

Решаем 655, 657, 659, 661

11.

Решаем 665, 667, 669

12.

Решаем 685, 687, 689

13.

Решаем 692, 694, 697

14.

Решаем 704, 709, 710

15.

Решаем 714, 716