Похожие презентации:
Катушка со стальным сердечником
1.
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТГРАЖДАНСКОЙ АВИАЦИИ
ИРКУТСКИЙ ФИЛИАЛ
КАФЕДРА АВИАЦИОННЫХ ЭЛЕКТРОСИСТЕМ И ПИЛОТАЖНОНАВИГАЦИОННЫХ КОМПЛЕКСОВ
ЛЕКЦИЯ № 1.2
по дисциплине
Теория электромагнитного поля
ТЕМА № 1
Катушка со стальным сердечником
2.
Вопросы лекции1.3. Катушка с магнитопроводом.
3.
1.3. Катушка с магнитопроводом.а). Эффективная индуктивность катушки с ферромагнитным
сердечником
При анализе различных режимов работы катушки с ферромагнитным
сердечником с использованием действующих токов и напряжений широко
используется параметр — эффективная (действующая) индуктивность. Для ее
введения несинусоидальные периодические токи и напряжения заменяются
эквивалентными синусоидальными. Тогда эффективная индуктивность
x
определяется следующим выражением:
L ЭФ
(5)
2
2
где x z r
- индуктивное сопротивление катушки.
Катушки с ферромагнитным сердечником имеют высокую добротность,
поэтому для них с высокой степенью точности можно принять
U ,
x z
I
т. е. рассматривать катушку как идеализированную.
При этом условии выражение (5) эффективной индуктиности определится
соотношением
U
LЭФ
I
19
4.
Вспоминаем• добротность контура или коэффициент
резонанса показывает во сколько раз
напряжение на индуктивности или на
емкости при резонансе больше, чем
напряжение, приложенное к цепи.
5.
С учетом (4) последняя формула примет вид:(4)
U UL 4.44fwФ0 m
wФ 0 0
LЭФ
I
I
17
,
(6)
где 0 и I - действующие потокосцепление и ток.
Обратимся к рис.2, на котором представлена веберамперная характеристика индуктивной катушки с
ферромагнитным сердечником, связывающая
действующие потокосцепление и ток. Из
характеристики следует, что по мере роста тока
отношение и, следовательно, эффективная
индуктивность вначале будут увеличиваться, а потом уменьшаться. Такой
характер изменения эффективной индуктивности объясняется насыщением
сердечника при возрастании тока катушки.
б). Мгновенный и действующий токи в идеализированной катушке с
ферромагнитным сердечником
Для определения характера изменения мгновенного тока в катушке с
ферромагнитным сердечником необходимо воспользоваться зависимостью
мгновенного потока от тока: Ф0 = f(i). При принятых условиях (отсутствие
гистерезиса) эта зависимость будет иметь вид, показанный на рис.3.
6.
16Рис. 3.Методика
построения кривой тока
i(t) по кривой Ф0 = f(i) и
графику изменения
Ф0(t) представлена на
рис. 3.
Напомним (см. формулу (3)), что в идеализированной катушке при
синусоидальном приложенном напряжении магнитный поток также изменяется
по синусоидальному закону. Поэтому на рис. 3,б функция Ф0(t) изображена
синусоидальной.
Последовательность построения кривой тока i(t) показана на рис. 3,б для
момента времени t1. Для этого момента времени определяем значение потока.
Сносим значение потока на кривую Ф0(i) и определяем значение тока для
данного потока. Полученное значение тока откладываем на временной
диаграмме (на ординате t1). На рис. 3,б показано также получение амплитуды
тока Im, соответствующей амплитуде потока Ф0m.
7.
15Рис. 3
Итак,
синусоидальное
напряжение,
приложенное к
идеализированной
катушке с
форромагнитным
сердечником при
условии его насыщения,
вызывает в ней синусоидальный поток и несинусоидальный периодический
ток.
Построим векторную диаграмму идеализированной катушки. Векторную
диаграмму, как известно, можно строить только для синусоидальных величин.
По этой причине несинусоидальный ток i(t) заменим эквивалентным
синусоидальным ip(t) (на рис. 3,б эта эквивалентная синусоида изображена
штриховой линией), действующее значение, которого равно действующему току
катушки, подсчитанному по формуле
Т
,
(7)
1 2
Iр
i dt
Т0
8.
Рис. 314
Т
1 2 ,
Iр
i dt
Т0
(7)
где
i(t) — несинусоидальный
периодический ток,
протекающий по катушке;
Iр - действующий
эквивалентный ток.
Угол сдвига фаз между синусоидальным напряжением u(t) и эквивалентным
синусоидальным током ip(t) определяется по (1*) и равен:
P
1
*
arccos
P
uidt U э I э cos э (1 )
2 ,
T
UI р
так как в идеализированной катушке потерь нет и Р=0.
Энергетический процесс в этом случае будет заключаться в колебании
энергии между источником и катушкой. Таким образом, ток i(t), проходящий
через катушку, будет только возбуждать магнитный поток Ф0(t). Поэтому ток
ip(t) называется реактивным, или намагничивающим (действующая его
величина Ip(t)).
9.
13После замены несинусоидального тока катушки i(t) эквивалентным
синусоидальным током ip(t) можно построить векторную диаграмму катушки,
изображенную на рис. 4. На векторной диаграмме вектор тока I р совпадает по
фазе с потоком и отстает от напряжения на 900. Вектор э.д.с. E L , согласно
выражению (2), равен по величине и противоположен по направлению вектору
.
U
Рис.4
10.
в). Влияние гистерезиса и вихревых токов на процессы в катушке сферромагнитным сердечником
12
Рассмотрим вначале влияние гистерезиса на характер изменения во времени
тока катушки. Для этого пренебрегаем потоком рассеяния катушки, ее активным
сопротивлением и вихревыми токами в сердечнике. Пусть к зажимам катушки
приложено напряжение u(t)= Umsin t. Тогда при принятых упрощениях
остается в силе выражение (3), согласно которому магнитный поток также будет
изменяться по синусоидальному закону. Кривая Ф0=Ф(i), устанавливающая
связь между потоком и током, в этом случае будет уже неоднозначна. На рис. 5
показана методика построения кривой тока i(t).
Um
(3)
Ф ( t)
sin( t ) Ф sin( t )
0
w
2
0m
2
Рис.5
Порядок построения кривой
i(t) остается тем же, что и для
идеализированной катушки, и
ведется для нескольких моментов
времени в пределах одного
полупериода изменения Ф0(t).
11.
11Рис.5
Из рассмотрения
полученной кривой i(t)
следует, что она искажается
еще больше по сравнению с
током в идеализированной
катушке (становится
несимметричной
относительно начала координат, чего не было в случае идеализированной
катушки) и, кроме того, момент прохождения потока через нуль отстает от
момента прохождения тока через нуль.
Максимумы тока и потока совпадают. Заменив несинусоидальную кривую
тока i(t) эквивалентной синусоидой i0(t) (на рис. 5 она изображена штриховой
линией), можно заметить, что она опережает по фазе на некоторый угол
синусоидальную функцию потока. При этом угол сдвига фаз между
синусоидой приложенного напряжения u(t) и эквивалентной синусоидой тока
i0(t) должен быть таким, чтобы средняя мощность за период осталась такой же,
как и в реальной катушке, т. е.
Т
1
P
uidt UI 0 cos
(8)
T 0
12.
10В формуле (8) I0 - действующий эквивалентный ток. Из выражения (8)
следует, что катушка с ферромагнитным сердечником, активное сопротивление
обмотки которой принято равным нулю, подключенная к сети переменного тока,
потребляет энергию. Это объясняется тем, что в этом случае будет иметь место
перемагничивание сердечника, связанное с потерей энергии, так как силы,
осуществляющие перемагничивание, преодолевают сопротивление со стороны
внутренних молекулярных сил ферромагнитного сердечника. Затраты энергии
на перемагничивание связаны с переходом энергии источника в тепло. Эти
потери называются потерями на г и с т е р е з и с. Мощность потерь на
перемагничивание сердечника определяется выражением
(9)
PГ SGfm B m H
где S — площадь петли гистерезиса; G — масса сердечника; f — частота
перемагничивающего поля; mB, mH — масштабы по осям графика В = В(Н).
Из выражения (9) следует, что для уменьшения потерь на гистерезис в
качестве материала для сердечников необходимо использовать те магнитомягкие
материалы, которые отличаются узкой петлей гистерезиса.
Учет потерь на гистерезис путем вычисления площади петли (по (9))
неудобен в практических расчетах. Для этой цели обычно используются
полуэмпирические формулы.
13.
Наибольшее распространение получила следующая формула дляопределения мощности потерь на гистерезис:
PГ Г GfB nm
9
(10)
где Г - коэффициент, зависящей от свойств материала сердечника, т. е. от
площади петли S, (находится опытным путем); G — масса сердечника;
Вm — амплитудное значение индукции;
n — показатель степени, зависящий, от величины Вm.
Если значения Вm находятся в пределах 1,0 — 1,6 Тл, то n = 2.
Потери на вихревые токи обусловливаются тем, что переменное магнитное
поле сердечника катушки индуктирует э.д.с. не только в самой катушке, но и в
сердечнике. В результате в сердечнике возникают индуктированные токи,
которые называются вихревыми. Вихревые токи согласно правилу Ленца
препятствуют изменению магнитного потока, т. е. оказывают на вызывающее их
поле размагничивающее действие. Чаще всего вихревые токи являются токами
паразитными, приводящими к нежелательному выделению в сердечнике
(магнитопроводы трансформаторов, электрических машин, магнитных
усилителей, дроссельных катушек и т. д.) тепловой энергии за счет источника
электрической энергии. Однако в некоторых случаях вихревые токи
используются для решения некоторых технических задач.
14.
8В частности, они используются в измерительных приборах (для успокоения
подвижной системы), в индукционных печах (для плавки металлов и сплавов) и
т. д.
Для уменьшения потерь от вихревых токов необходимо (при заданной
частоте f и амплитуде индукции Вm) увеличивать электрическое сопротивление
ферромагнитного сердечника. Это достигается разделением контуров вихревых
токов на ряд отдельных листов, изолированных друг от друга. Иногда железные
сердечники для этих же целей собираются из тонких электрически
изолированных друг от друга стальных проволок. Кроме того, в состав железа
добавляются специальные присадки (например, кремний), увеличивающие
удельное сопротивление железа. Таким образом, удается снизить тепловое и
размагничивающее действия вихревых токов до допустимого значения. С этой
же целью для радиочастот применяются сердечники, изготовленные из
магнитодиэлектриков. Магнитодиэлектрики представляют собой
ферромагнитный порошок, частицы которого связаны диэлектриком. Широкое
применение получили также ферритовые сердечники — ферромагнитные
полупроводниковые материалы, электропроводность которых в миллионы раз
меньше электропроводности металлических ферромагнетиков. По этой причине
такие материалы применяются в настоящее время на высоких и даже
сверхвысоких частотах.
15.
В авиационном оборудовании в основном используются магнитные цепи,состоящие из стальных (листовых, ленточных) расслоенных сердечников.
Мощность потерь на вихревые токи в них определяется по формуле
(11)
P Gf 2 B2 ,
В
В
7
m
где в — коэффициент, зависящий от сорта стали (удельной проводимости)
и толщины стальных листов; f - частота магнитного потока; Вm - амплитудное
значение индукции; G — масса сердечника.
Формула (11) достаточно точно определяет также потери в сердечнике из
ферромагнитного порошка с диэлектрическим связующим веществом. На
основании (11) и (10) суммарные потери в ферромагнитных сердечниках
(потери в стали) от гистерезиса и вихревых токов определяются следующим
соотношением:
Pc PГ PВ .
(12)
Учет потерь в магнитных сердечниках приводит к тому, что ток катушки (у
катушки пока не учтены активное сопротивление и поток рассеяния) будет
отставать по фазе от приложенного напряжения на угол, меньший 900.
Векторная диаграмма для этого случая изображена на рис. 6.
16.
6Рис.6
Угол сдвига фаз между током и потоком
носит название угла потерь.
На рис. 6 ток представлен в виде двух
составляющих. Составляющая (совпадающая
по фазе с потоком ) как было показано ранее,
обеспечивает возбуждение в сердечнике
основного потока Ф0. Составляющая
(совпадающая по фазе с напряжением UL)
возникает при наличии потерь в
ферросердечнике и при заданном напряжении определяет величину этих
потерь.
17.
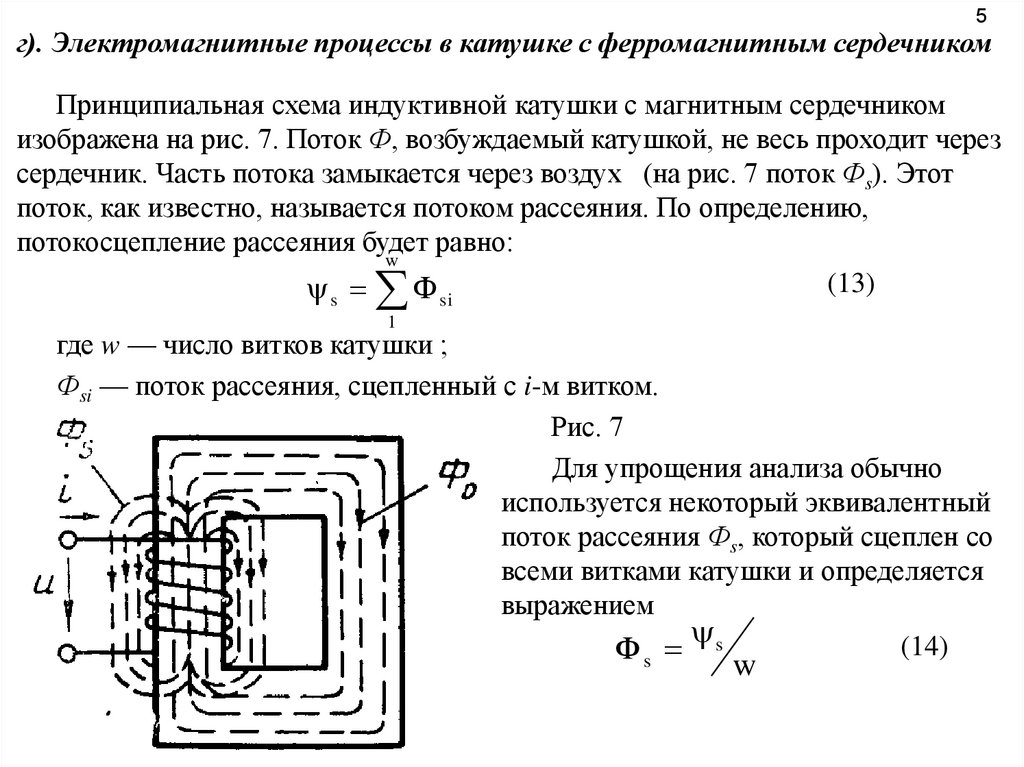
5г). Электромагнитные процессы в катушке с ферромагнитным сердечником
Принципиальная схема индуктивной катушки с магнитным сердечником
изображена на рис. 7. Поток Ф, возбуждаемый катушкой, не весь проходит через
сердечник. Часть потока замыкается через воздух (на рис. 7 поток Фs). Этот
поток, как известно, называется потоком рассеяния. По определению,
потокосцепление рассеяния будет равно:
w
(13)
s Ф si
1
где w — число витков катушки ;
Фsi — поток рассеяния, сцепленный с i-м витком.
Рис. 7
Для упрощения анализа обычно
используется некоторый эквивалентный
поток рассеяния Фs, который сцеплен со
всеми витками катушки и определяется
выражением
(14)
Фs s
w
• .
(14)
18.
4Следовательно, потокосцепление рассеяния равно:
s wФs .
Вследствие того, что магнитное сопротивление воздушного участка потока
рассеяния во много раз превосходит сопротивление участка из ферромагнитного
материала, сопротивлением последнего можно пренебречь и считать, что поток
Фs проходит по воздуху. По этой причине поток рассеяния Фs и
потокосцепление рассеяния s считаются пропорциональными току и
определяются следующим образом:
s wФs Lsi
(15)
где Ls = const — индуктивность рассеяния, постоянный параметр.
Таким образом, реально существующий поток Ф катушки с сердечником для
удобства анализа разбивается на два потока: поток рассеяния Фs,
пропорциональный току и совпадающий с ним по фазе, и основной поток Ф0,
связанный с током кривой намагничивания и замыкающийся через
ферромагнитный сердечник. На основании изложенного, катушку с
сердечником, изображенную на рис. 7, можно представить в виде рис. 8,
удобного для анализа.
19.
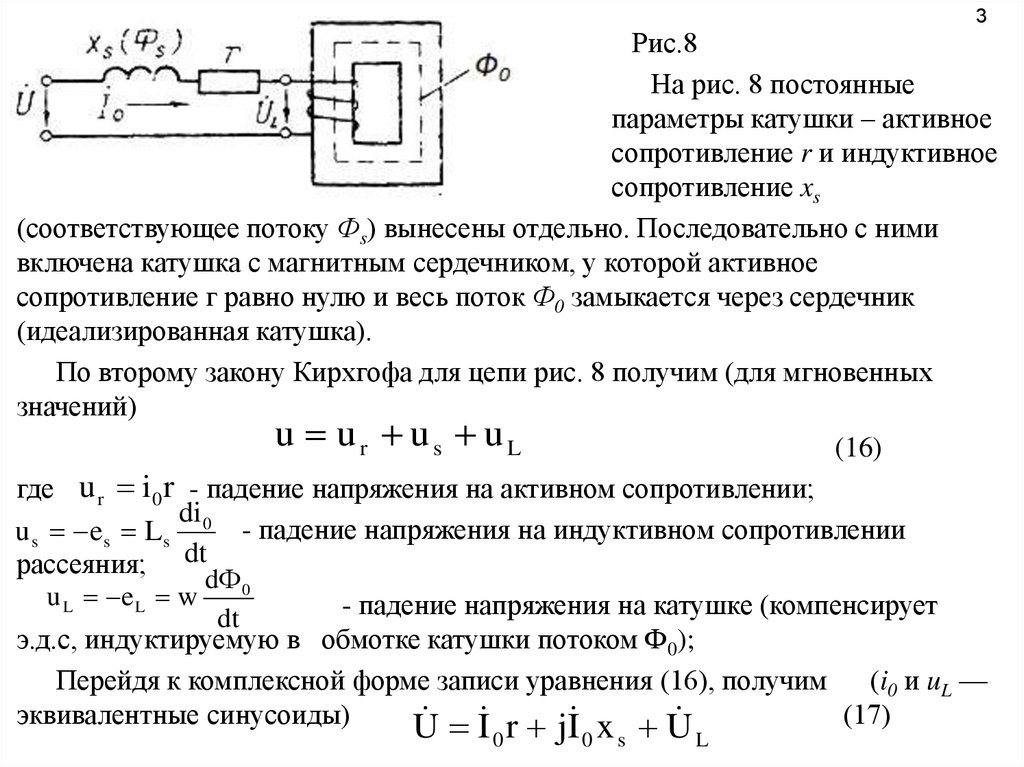
3Рис.8
На рис. 8 постоянные
параметры катушки – активное
сопротивление r и индуктивное
сопротивление xs
(соответствующее потоку Фs) вынесены отдельно. Последовательно с ними
включена катушка с магнитным сердечником, у которой активное
сопротивление г равно нулю и весь поток Ф0 замыкается через сердечник
(идеализированная катушка).
По второму закону Кирхгофа для цепи рис. 8 получим (для мгновенных
значений)
u ur us uL
(16)
где u r i 0 r - падение напряжения на активном сопротивлении;
di
u s es L s 0 - падение напряжения на индуктивном сопротивлении
рассеяния; dt
dФ 0
u L e L w
- падение напряжения на катушке (компенсирует
dt
э.д.с, индуктируемую в обмотке катушки потоком Ф0);
Перейдя к комплексной форме записи уравнения (16), получим (i0 и uL —
эквивалентные синусоиды)
(17)
I r j I x U
U
0
0
s
L
20.
2Уравнению (17) можно поставить в соответствие схему замещения катушки с
ферромагнитным сердечником, изображенную на рис. 9. В эту схему, кроме уже
упоминавшихся r и xs. входят следующие параметры, отображающие свойства
катушки с ферросердечником: rс — активное сопротивление сердечника
(мощность потерь в этом сопротивлении равна мощности потерь в
ферромагнитном сердечнике от гистерезиса и вихревых токов), х0 - индуктивное
сопротивление катушки.
Рис.9
Данная схема замещения описывает
поведение реальной катушки
индуктивности, у которой есть потери
на гистерезис и вихревые токи, сама
катушка обладает активным
сопротивлением, и в катушке
существует поток рассеяния.
21.
1Применим уравнение 17 для построения векторной диаграммы реальной
катушки (рис. 10). Угол, обусловленный гистерезисом
. Практически
φ+δ=90º или δ=90º - φ. Коэффициент мощности
(18). Активная мощность катушки с
ферромагнитным сердечником состоит из потерь мощности в проводах Рs и в
магнитопроводе Рст
.
(19)
Чем больше угол δ, тем больше активная составляющая тока Ic и потери в
магнитопроводе. Поэтому угол δ называют углом
потерь в магнитопроводе.
На рис.10 приведена векторная схема для схемы
замещения рис. 9.
На диаграмме представлены сумма векторов токов
и сумма векторов напряжений (падений
напряжений)
Рис.10
22.
заключениеТ. о., в результате рассмотрения материала вы получили знания :
• О катушке с магнитопроводом;
• эффективной индуктивности катушки с ферромагнитным сердечником;
• мгновенном и действующем токах в идеализированной катушке с
ферромагнитным сердечником;
• влиянии гистерезиса и вихревых токов на процессы в катушке с
ферромагнитным сердечником;
• электромагнитных процессах в катушке с ферромагнитным сердечником.




















 Физика
Физика








