Представление числовой информации с помощью систем счисления. Перевод чисел из одной системы счисления в другую

1.

ПРЕЗЕНТАЦИЯ К УРОКУ В 10 КЛАССЕ
Спиридонова Елена Васильевна
Учитель информатики и математики
МОУ-СОШ №6
г. Петровск-Забайкальский
2023 г

2.

«Мысль – выражать все
числа немногими знаками,
придавая им значение по форме,
еще значение по месту, настолько
проста, что именно из-за этой
простоты трудно оценить,
насколько она удивительна …»
Пьер Симон Лаплас

3.

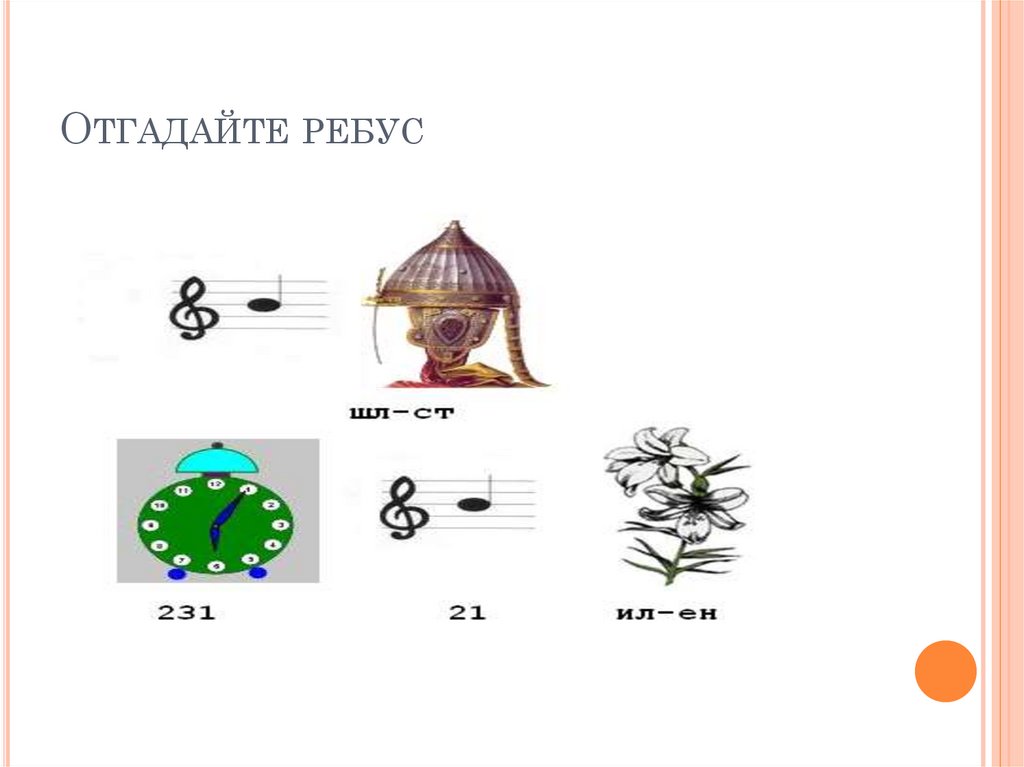
ОТГАДАЙТЕ РЕБУС

4.

РЕШЕНИЕ: СИ (ШЛЕМ – СТЕМ ) (ЧАСЫ 2
– А, 3-С, 1 – Ч), СИ- ИС, ЛИЛИЯ –
ЛЕНИЯ
(ОТВЕТ: СИСТЕМА СЧИСЛЕНИЯ).

5.

ВОПРОСЫ
1. Римское число CXXVII. Какую величину оно
выражает?
2. Системы счисления, основанные на
позиционном принципе, возникли независимо
одна от другой в древнем Междуречье
(Вавилон), у племени Майя и, наконец, в
Индии. Все это говорит о том, что
возникновение позиционного принципа не
было случайностью. Каковы же были
предпосылки для его создания? Что привело
людей к этому замечательному открытию?
3. 3FA4 - это число?
4. Кто и когда считал пятерками и дюжинами?

6.

ТЕМА УРОКА
«ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ
ИНФОРМАЦИИ С ПОМОЩЬЮ
СИСТЕМ СЧИСЛЕНИЯ.
ПРАКТИЧЕСКАЯ РАБОТА № 13.
ПЕРЕВОД ЧИСЕЛ ИЗ ОДНОЙ
СИСТЕМЫ СЧИСЛЕНИЯ В ДРУГУЮ С
ПОМОЩЬЮ КАЛЬКУЛЯТОРА»

7.

Система
счисления - это способ
записи чисел с помощью цифр.
Система счисления — это
знаковая система, в которой числа
записываются по определенным
правилам с помощью знаков
некоторого алфавита, называемых
цифрами.

8.

НЕМНОГО ИЗ ИСТОРИИ
фильм

9.

СИСТЕМА СЧИСЛЕНИЯ — ЭТО ЗНАКОВАЯ СИСТЕМА, В КОТОРОЙ ЧИСЛА
ЗАПИСЫВАЮТСЯ ПО ОПРЕДЕЛЕННЫМ ПРАВИЛАМ С ПОМОЩЬЮ ЗНАКОВ
НЕКОТОРОГО АЛФАВИТА, НАЗЫВАЕМЫХ ЦИФРАМИ.
Все известные системы счисления делятся на
позиционные и непозиционные. Непозиционные
системы счисления возникли раньше позиционных.
Последние являются в свою очередь результатом
длительного исторического развития непозиционных
систем счисления.
Непозиционной называется такая система счисления,
у которой количественный эквивалент («вес») цифры не
зависит от ее местоположения в записи числа.
1) Единичная система счисления.
2) Древнеегипетская десятичная непозиционная
система счисления.
3) Римская система счисления.
I-1, V-5, Х- 10, L-50, С- 100, D-500, М - 1000.
Пример: XXXVI
4) Древнегреческая нумерация.
1 — α, 2 — β, 7 — ζ, 40 — μ.

10.

ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ.
Позиционной называется такая система счисления, в
которой количественный эквивалент («вес») цифры
зависит от ее местоположения в записи числа.
Числа в позиционных системах счисления
записываются в виде суммы числового ряда
степеней основания, в качестве коэффициентов
которых выступают цифры данного числа.
Пример.
Рассмотрим число 222.
В записи этого числа используется трижды цифра 2. Но
вклад каждой цифры в величину числа разный. Первая
2 означает число сотен, вторая — число десятков, третья
— число единиц. Если сравнить «вес» каждой цифры в
этом числе, то получиться, что первая 2 «больше» второй
в 10 раз и «больше» третьей в 100 раз. Этот принцип
отсутствует в непозиционных системах счисления.

11.

Основание (базис) позиционной системы
счисления — это количество цифр или других
знаков, используемых для записи чисел в данной
системе счисления.
Давайте вспомним развернутую форму записи
числа:
54310 = 5 * 102 + 4 * 101 + 3 * 100
свернутая форма
развернутая форма
333,3310=3*102+3*101+3*100+3*10-1+3*10-2
Умножение или деление десятичного числа на 10
(величину основания) приводит к перемещению
запятой, отделяющей целую часть от дробной, на
один разряд вправо или влево. Например:
333,3310*10=3333,310,
333,3310:10=33,33310.

12.

ОСНОВНЫЕ ДОСТОИНСТВА ЛЮБОЙ
ПОЗИЦИОННОЙ СИСТЕМЫ СЧИСЛЕНИЯ:
1. простота выполнения арифметических операций;
2. ограниченное количество символов, необходимых для записи
числа.
Позиционная система записи чисел удобна и экономична не
только для записи чисел знаками на бумаге и для выполнения
над ними арифметических действий. Она удобна и для
механического представления чисел. Вспомним, например, счеты.
Каждому разряду числа (единицам, десяткам, сотням, тысячам и
т.д.) на счетах соответствует своя проволока. Костяшки на этой
проволоке могут занимать десять различных положений
(одиннадцатое положение — когда все десять косточек находятся
с левой стороны — допускается лишь в середине вычислений, а в
конце их является запретным: все десять косточек должны быть
переброшены направо, а на следующей по старшинству проволоке
одна косточка переброшена справа налево).
Позиционных систем очень много, так как за основание системы
счисления можно принять любое число не меньшее 2.

13.

— ВСПОМНИТЕ, КАК КОДИРУЕТСЯ ИНФОРМАЦИЯ В КОМПЬЮТЕРЕ?
(С ПОМОЩЬЮ ДВОИЧНОГО КОДИРОВАНИЯ, Т.Е. ЛЮБАЯ
ИНФОРМАЦИЯ ПРЕДСТАВЛЯЕТСЯ В ВИДЕ ПОСЛЕДОВАТЕЛЬНОСТИ
0 И 1.)
Давайте вспомним двоичную систему счисления.
Основание – 2, алфавит цифр – 0,1. Числа в
двоичной системе в развернутой форме
записываются в виде суммы ряда степеней
основания 2 с коэффициентами, в качестве которых
выступают цифры 0 и 1. Запишем развернутую
форму двоичного числа:
1011,0112=1*23+0*22+1*21+1*20+0*2-1+1*2-2+1*2-3
Умножение или деление двоичного числа на 2
(величину основания) приводит к перемещению
запятой, отделяющей целую часть от дробной, на
один разряд вправо или влево. Например:
11011,1012*2=110111,012,
11011,1012:2=1101,11012.

14.

РЕШЕНИЕ ЗАДАНИЯ НА ПЕРЕВОД ЧИСЕЛ
ИЗ ОДНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В
ДРУГУЮ.
14_8:
Разбор задания 14 ЕГЭ по
информатике (с сайта К. Полякова,
вариант 38):
Найдите основание системы
счисления, в которой выполнено
сложение:
144 + 24 = 201

15.

Запишем формулу перевода в десятичную систему
счисления каждого из слагаемых и сумму исходного
равенства: 144 + 24 = 201
1*x2 + 4*x1 + 4*x0 + 2*x1 + 4*x0 = 2*x2 + 0*x1 + 1*x0
Упростим полученное уравнение: x 2 - 6x - 7 = 0
Решим уравнение: D = b2 - 4ac = 36 - 4*1*(-7) = 64
x = (-b ± √D)/2a
x1 = (6 + 8)/2 = 7
x2 = (6 - 8)/2 - не подходит
Ответ: 7

16.

ВОПРОСЫ:
Чем
отличаются позиционные системы
счисления от непозиционных?
Каково основание десятичной системы
счисления?
Какие цифры входят в алфавит
десятичной системы счисления?
Двоичной системы счисления?
На какую величину в позиционных
системах счисления различаются цифры
соседних разрядов числа?

17.

САМОСТОЯТЕЛЬНАЯ РАБОТА
1 вариант
1. Представьте числа
в развернутой
форме:
305(10); 153,25(6);
10000011(2); 671,24(8).
2. Переведите числа,
используя
Калькулятор:
110001110(2)→ N(10),
N(8), N(16);
19865(10)→ N(2), N(16).
2вариант
1. Представьте числа
в развернутой
форме:
306(10); 143,25(6);
10001011(2); 771,24(8).
2. Переведите числа,
используя
Калькулятор:
100001110(2)→ N(10),
N(8), N(16);
19965(10)→ N(2), N(16).

18.

Д.З. П. 1.5.1. ВОПРОСЫ