Линейная функция и ее график. Решение задач

1. Линейная функция и ее график.

Решение задач

2. Какие функции являются линейными?

5
u = -3v + 1
у 3
х
s = 2t – 8
6
у 2 3
х
у = 7 – 5х
у = 9х
у х 3
f = 5 – g3
2

3. Линейная функция:

у = kx + b
Назвать k и b.
у = 5х + 8
у = -3х + 2
у = 4х - 3
k = 5; b = 8
k = -3; b = 2
k = 4; b = -3
у = 7х
у = -х - 9
у = 2,5
k = 7; b = 0
k = -1; b = -9
k = 0; b = 2,5

4.

В уравнении y = kx + b k – угловой
коэффициент отвечает за наклон графика.
• Если k > 0 – график наклонен вправо
(проходит в 1-ой и 3-ей четвертях)
• Если k < 0 – график наклонен влево (2-ая и 4ая четверть)
Коэффициент b отвечает за сдвиг графика
вдоль оси ОУ.
• Если b > 0, то график получаем сдвигом
графика у = kx вверх на b единиц
• Если b < 0, то график получаем сдвигом
графика у = kx вниз на b единиц

5. Графики каких функций проходят через начало координат?

у = 7х
g = 2f
y = -5х + 1
y = -4x
s = -3t
s = 4t – 3
u = 4v -2
f = 9g + 2

6. Графики каких функций находятся в

II и IV четвертях
I и III четвертях
у = 2х
у = -5х
у = -6х
у=х
у = 8х
у = -1,5х
у = -(-3х)
-у = 4х

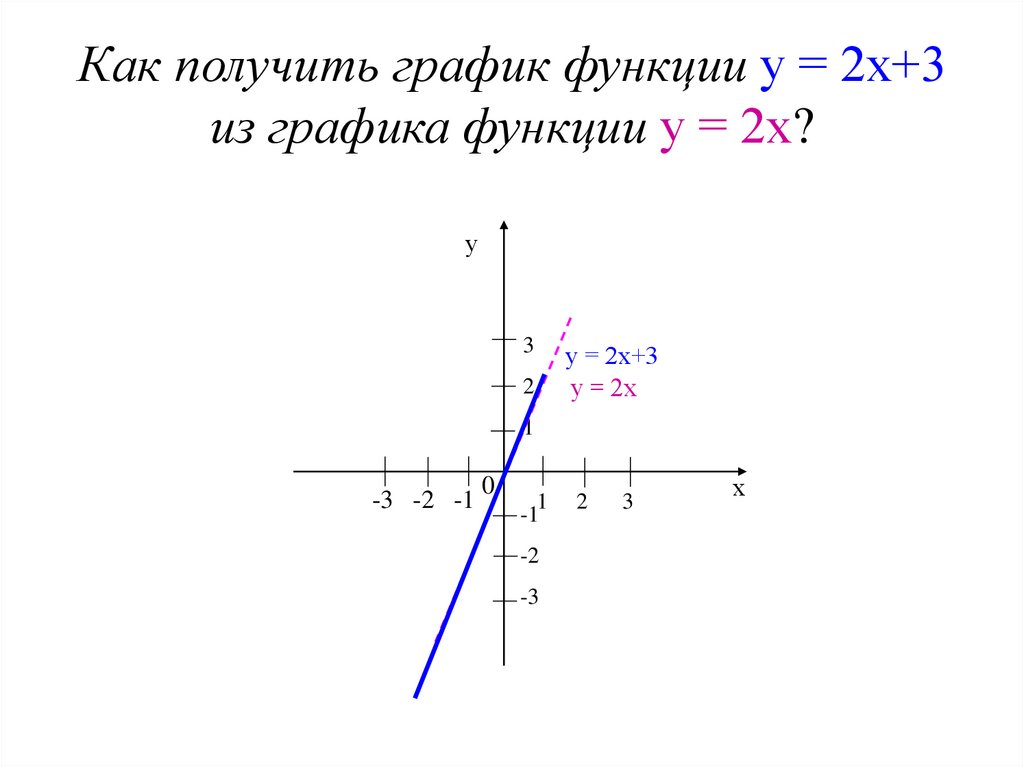
7. Как получить график функции у = 2х+3 из графика функции у = 2х?

у
3
2
у = 2х+3
у = 2х
1
-3 -2 -1
0
1
-1
-2
-3
2
3
х

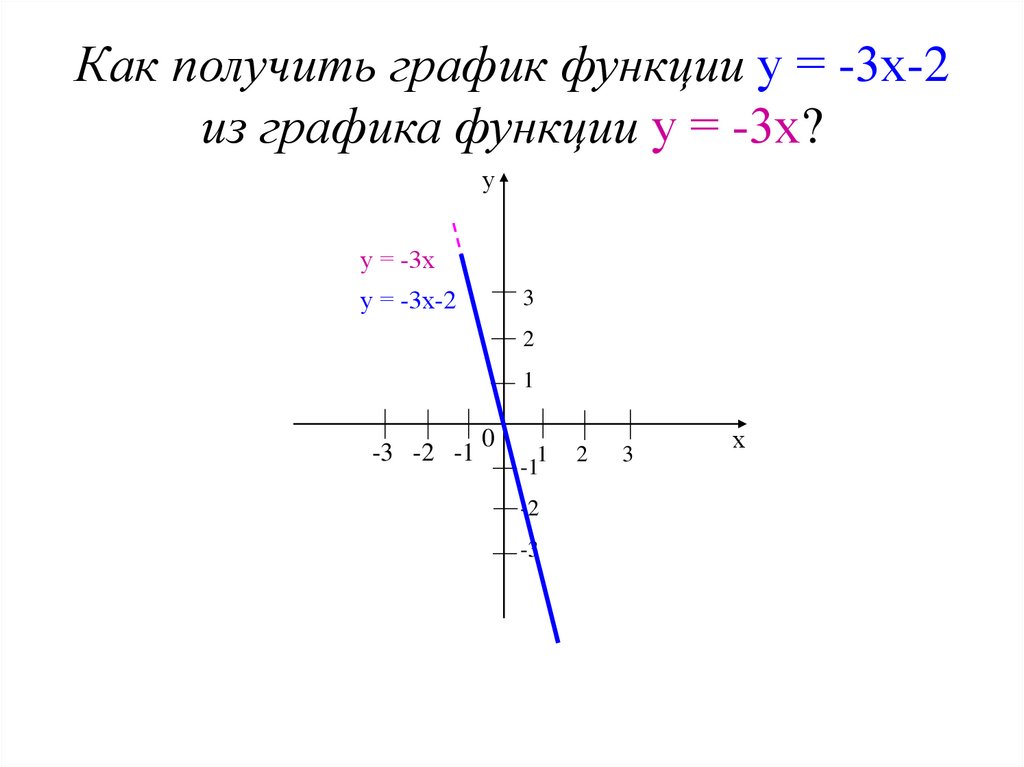
8. Как получить график функции у = -3х-2 из графика функции у = -3х?

у
у = -3х
у = -3х-2
3
2
1
-3 -2 -1
0
1
-1
-2
-3
2
3
х

9. Решить линейные уравнения:

х – 3 = 5,
х = 8.
х + 2 = -7,
х = -9.
2х - 1 = -13,
х = -6.
8х + 2 = 5,
3
х= .
8
5х = 0,
х = 0.
6 - 3х = 3,
х = 1.
14х + 2 = 9,
х = 0,5.

10. Задание №1 Дана функция у = 5х – 2

1. Найти: у(0) = 5·0 - 2 = 0 – 2 = -2
у(2) = 5·2 - 2 = 10 – 2 = 8
у(-3) = 5·(-3) - 2 = -15 - 2 = -17

11.

2. Найти значения х, при которых
значение функции у = 5х – 2 равно 23; 0.
у(х) = 23
у(х) = 0
23 = 5х – 2,
5х – 2 = 23,
5х = 23 + 2,
5х = 25,
х = 5.
0 = 5х – 2,
5х – 2 = 0,
5х = 0 + 2,
5х = 2,
х = 0,4.
Ответ: у(х) = 23 при х = 5. Ответ:
у(х) = 0 при х = 0,4.

12.

3. Выяснить, проходит ли график функции
у = 5х - 2 через точки А(3; 13), В(-1; 3).
А(3; 13)
13 = 5 · 3 – 2,
13 = 15 – 2,
13 = 13, верно график функции у = 5х – 2
проходит через точку А(3;13).
В (-1; 3)
3 = 5 · (-1) – 2,
3 = -5 – 2,
3 = -7, неверно график функции у = 5х – 2
не проходит через точку В(-1;3).

13. Задание №2.

Найти точки пересечения с осями
координат и построить график функции
у = 0,5х + 3.
С осью Ох: у = 0
0 = 0,5х + 3,
0,5х = -3,
х = -3 : 0,5,
х = -6.
(-6; 0)
С осью Оу: х = 0
у = 0,5 · 0 + 3,
у = 0 + 3,
у = 3.
(0; 3)

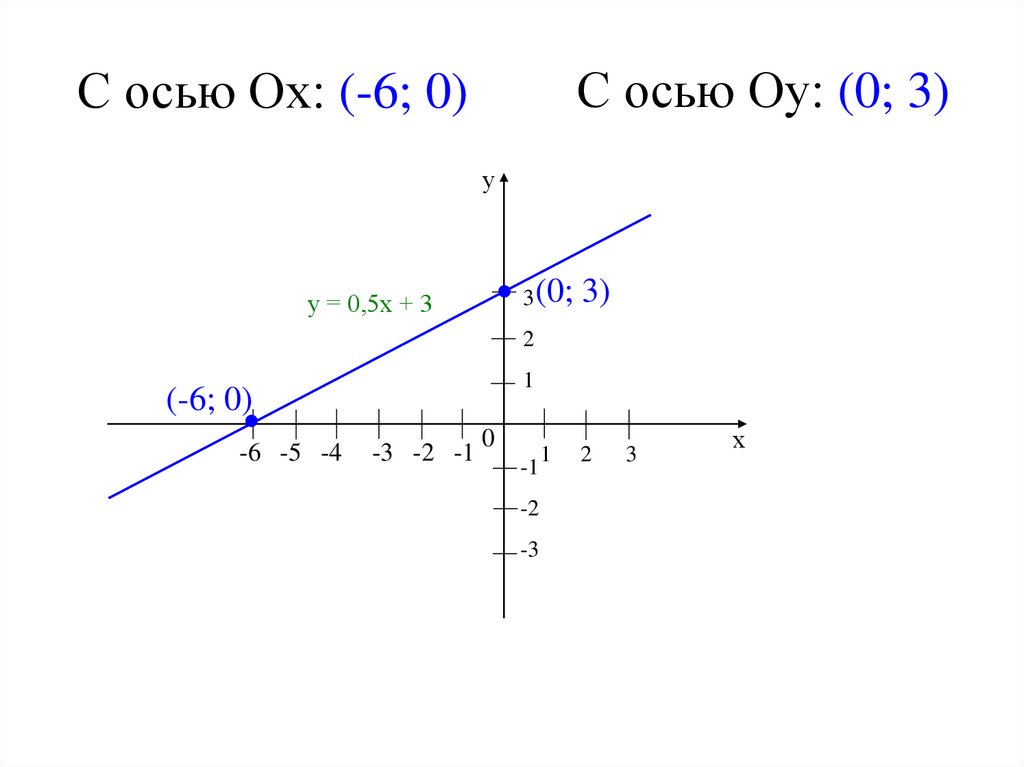
14.

С осью Оу: (0; 3)
С осью Ох: (-6; 0)
у
у = 0,5х + 3
3)
2
1
(-6; 0)
-6 -5 -4
3 (0;
-3 -2 -1
0
-1
-2
-3
1
2
3
х

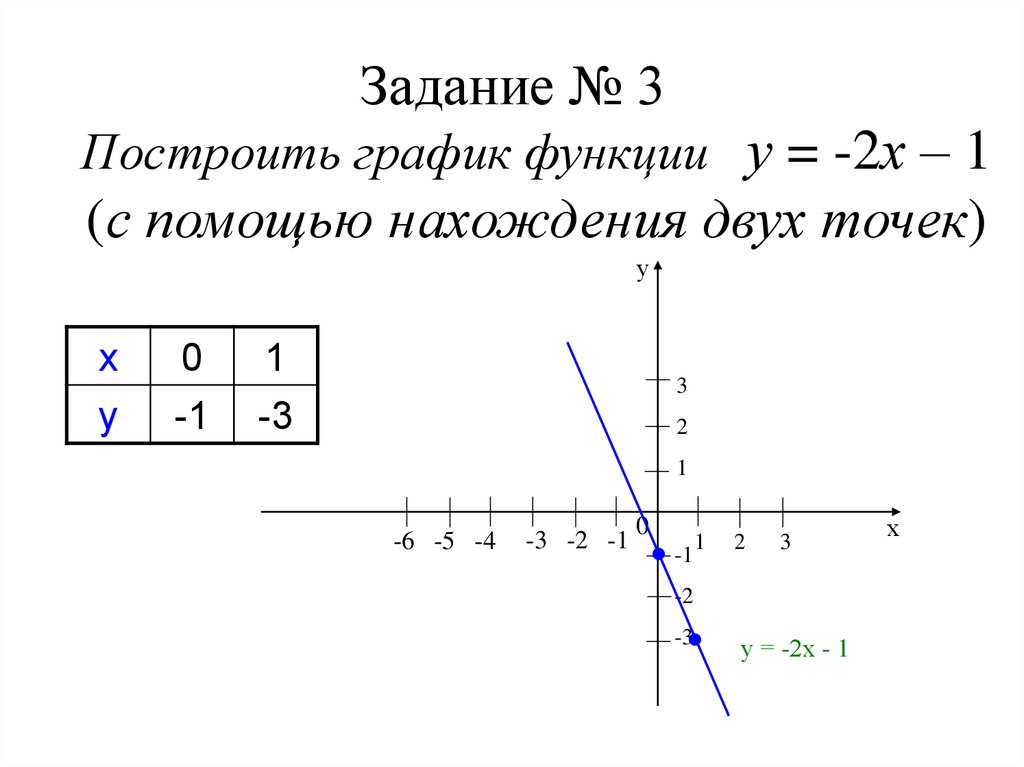
15. Задание № 3

Построить график функции у = -2х – 1
(с помощью нахождения двух точек)
у
х
у
0
-1
1
-3
3
2
-6 -5 -4
-3 -2 -1
1
0
-1
1
2
3
-2
-3
у = -2х - 1
х

16. Задание № 4

Найти значение b, если известно, что график
функции у = 4х + b проходит через точку А (1; 7).
у = 4х + b,
А (1; 7)
7 = 4·1 + b,
b = 7 - 4,
b = 3.
Ответ: b = 3.

17. Задание № 5

Найти значение k, если известно, что график
функции у = kх -2 проходит через точку В (2; 12).
у = kх - 2,
В (2; 12)
12 = k·2 - 2,
2k = 12 + 2,
2k = 14,
k = 7.
Ответ: k = 7.

18. Задание № 6

Найти координаты точки пересечения графиков
функций у = 1 - 2х и у = х – 5.
у = 1 – 2х, у = х - 5,
1 – 2х = х – 5,
2х + х = 1 + 5,
3х = 6,
х = 2.
у =1 – 2 ·2 = 1 – 4 = -3.
Ответ: (2; -3).

19. Домашнее задание: