Похожие презентации:
Линейная функция и её график. Алгебра, урок № 24
1.
Алгебра, урок № 242. Устная работа
УСТНАЯ РАБОТАКакая функция
называется линейной?
Функция вида у = kx + b
называется линейной.
Что является графиком
линейной функции
Графиком линейной
функции является прямая.
Сколько точек
необходимо и
достаточно для
построения графика
линейной функции?
Для построения прямой
необходимы только две
точки, так как через две
точки проходит
единственная прямая.
3. Устная работа: Какие из перечисленных уравнений являются линейными:
УСТНАЯ РАБОТА:КАКИЕ ИЗ ПЕРЕЧИСЛЕННЫХ
УРАВНЕНИЙ ЯВЛЯЮТСЯ
ЛИНЕЙНЫМИ:
Упражнения :
№8.1; 8.9
4.
y = kx + b – линейная функциях – аргумент (независимая
переменная)
у – функция (зависимая
переменная)
k, b – числа (коэффициенты)
к≠0
5. построить график линейной функции у = - 2х + 3
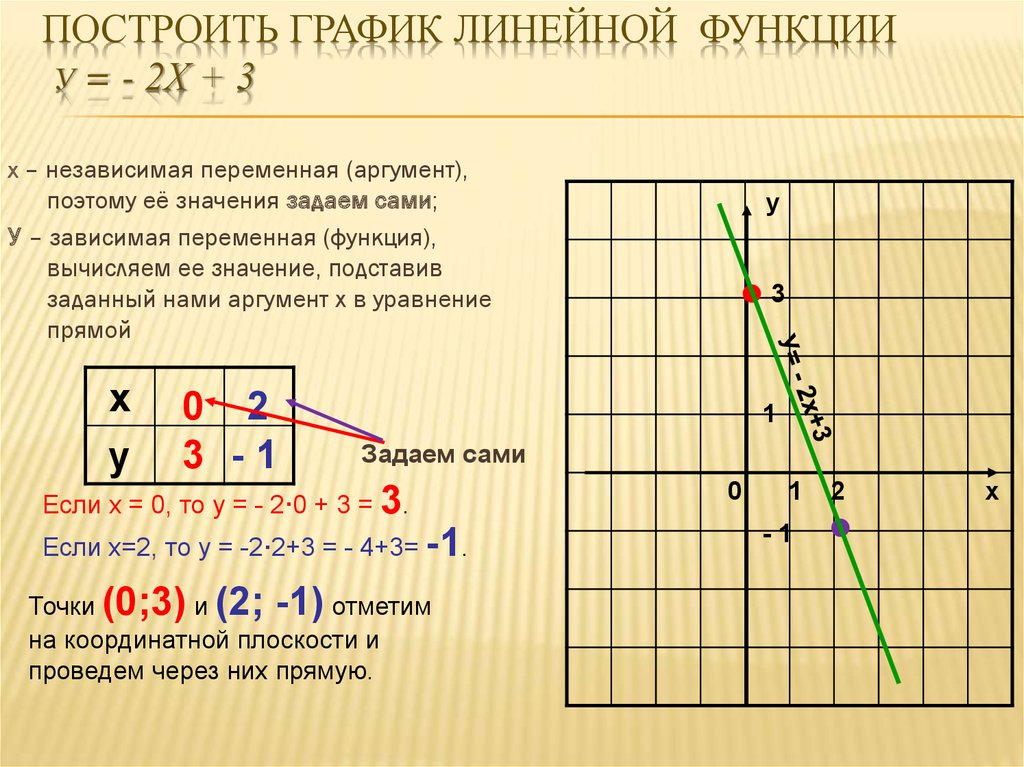
ПОСТРОИТЬ ГРАФИК ЛИНЕЙНОЙ ФУНКЦИИУ = - 2Х + 3
х – независимая переменная (аргумент),
поэтому её значения задаем сами;
У – зависимая переменная (функция),
вычисляем ее значение, подставив
заданный нами аргумент х в уравнение
прямой
х
у
0 2
3 -1
у
3
1
Задаем сами
Если х = 0, то у = - 2·0 + 3 = 3.
Если х=2, то у = -2·2+3 = - 4+3= -1.
Точки (0;3) и (2; -1) отметим
на координатной плоскости и
проведем через них прямую.
0
1
-1
2
х
6.
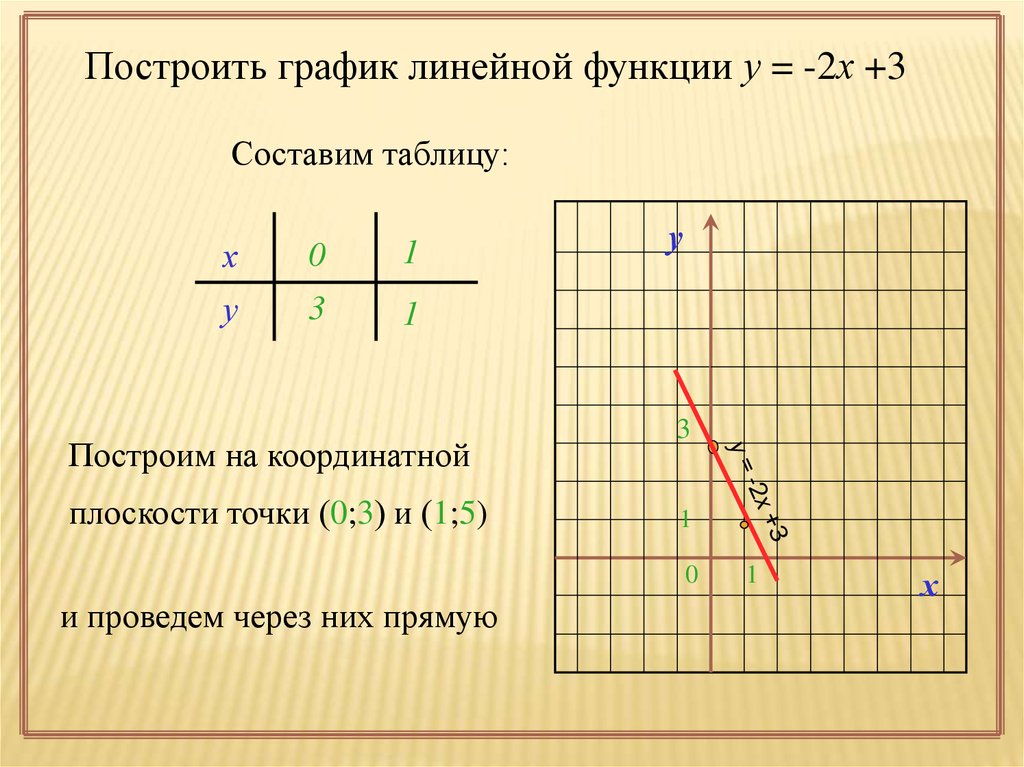
Построить график линейной функции у = -2х +3Составим таблицу:
х
0
1
у
3
1
Построим на координатной
плоскости точки (0;3) и (1;5)
у
3
1
0
и проведем через них прямую
1
х
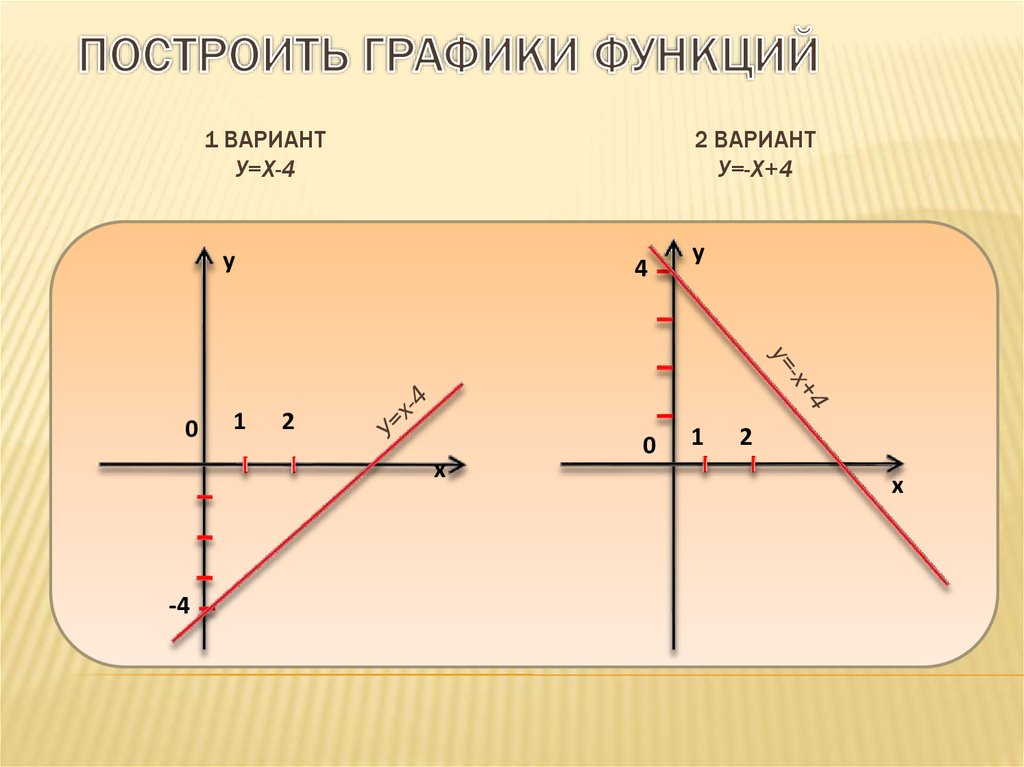
7. Построить графики функций
1 ВАРИАНТУ=Х-4
2 ВАРИАНТ
У=-Х+4
y
0
1
4
2
x
-4
0
y
1
2
x
8.
у0
у
х
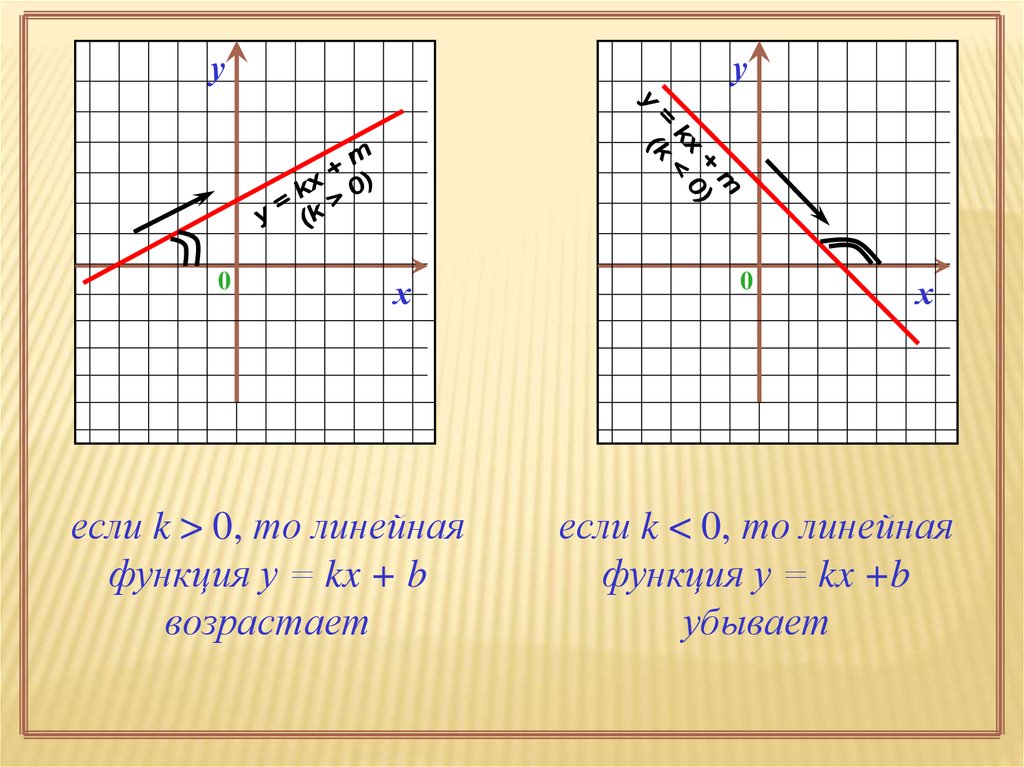
если k > 0, то линейная
функция у = kx + b
возрастает
0
х
если k < 0, то линейная
функция у = kx +b
убывает
9.
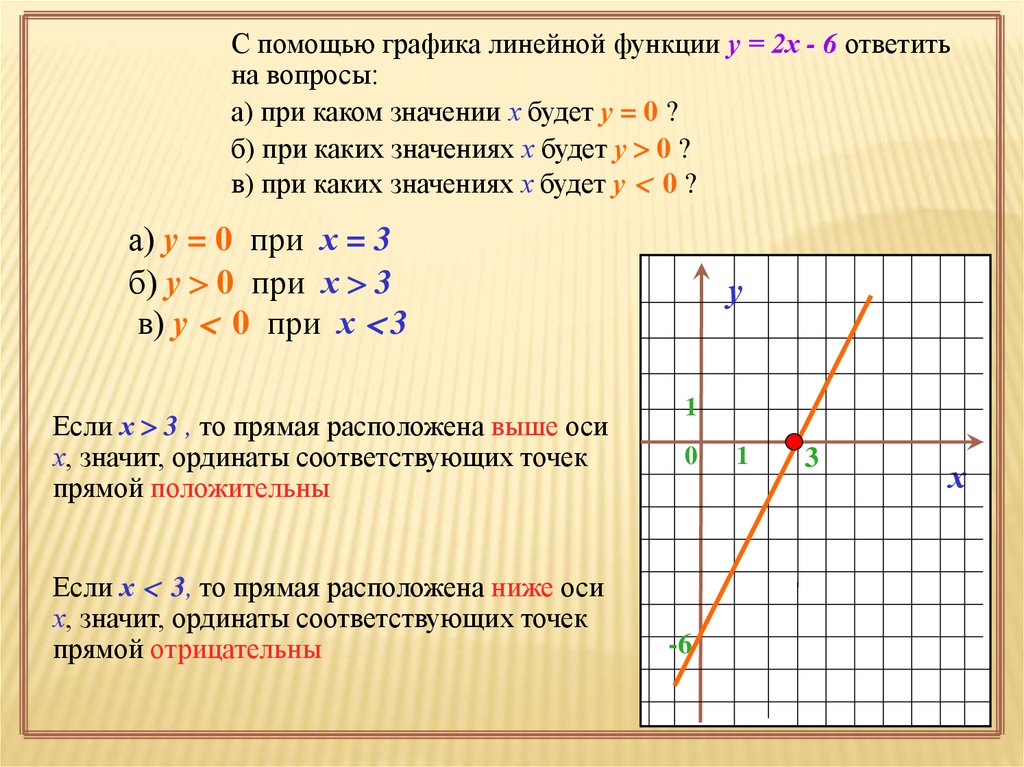
С помощью графика линейной функции у = 2х - 6 ответитьна вопросы:
а) при каком значении х будет у = 0 ?
б) при каких значениях х будет у 0 ?
в) при каких значениях х будет у 0 ?
а) у = 0 при х = 3
б) у 0 при х 3
в) у 0 при х 3
Если х 3 , то прямая расположена выше оси
х, значит, ординаты соответствующих точек
прямой положительны
Если х 3, то прямая расположена ниже оси
х, значит, ординаты соответствующих точек
прямой отрицательны
у
1
0
-6
1
3
х
10.
Самостоятельная работаПостроить графики функций:
1 вариант
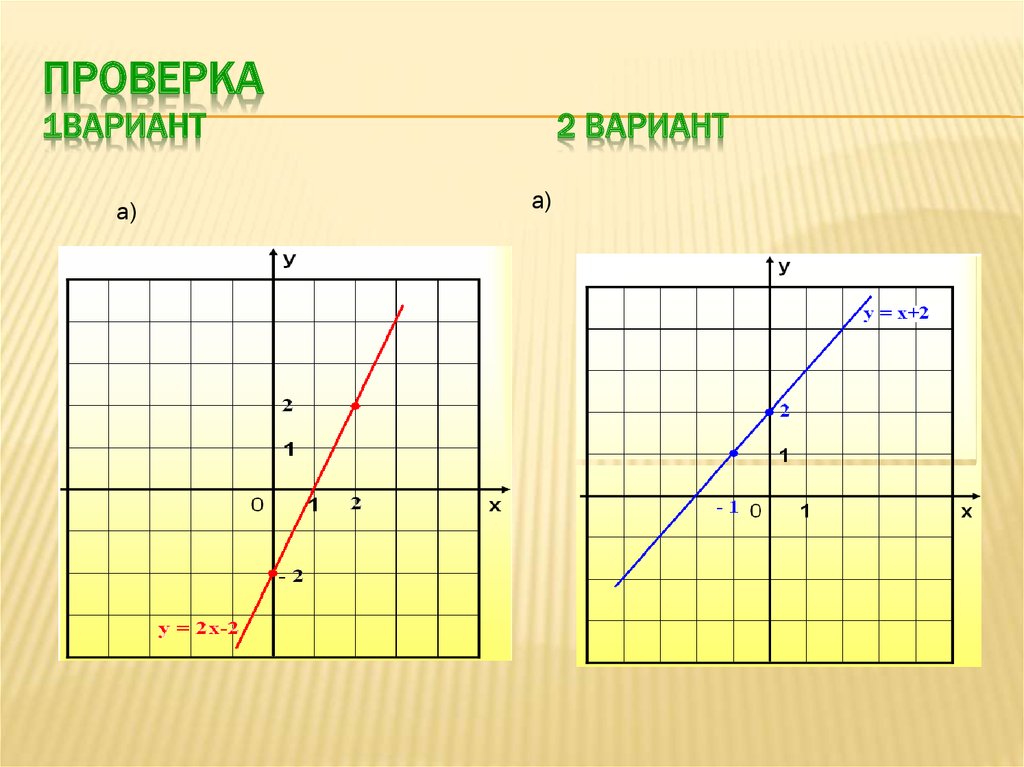
а) у = 2х – 2
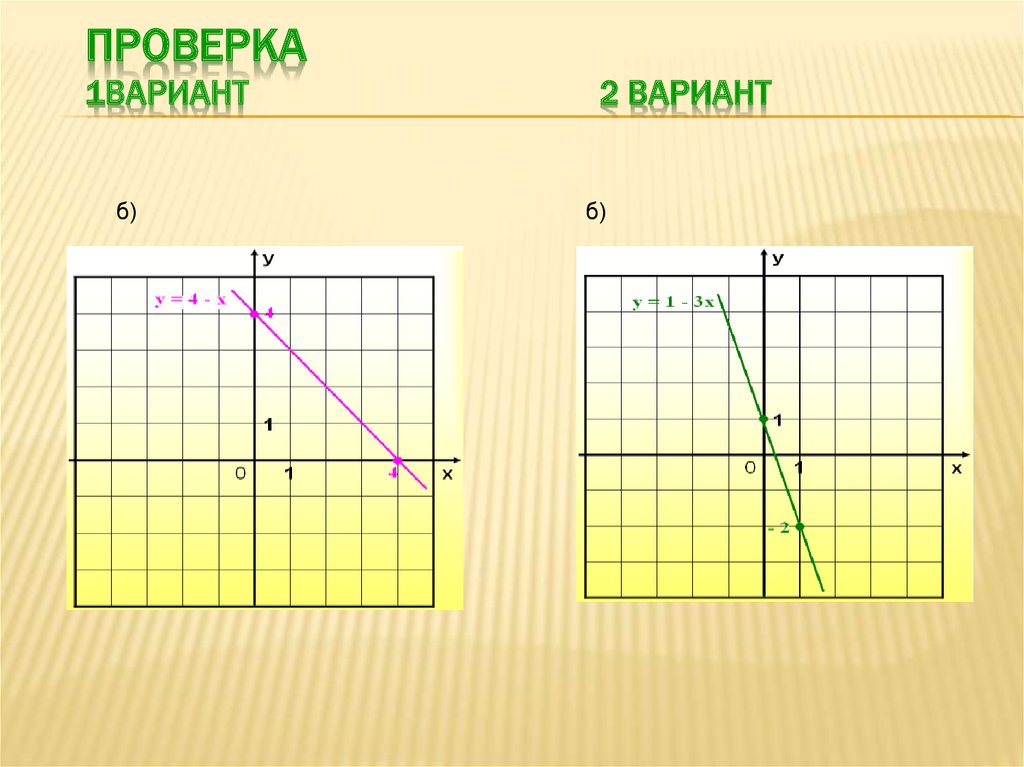
б) у = 4 – х
Вариант 2
а)у = х + 2
б) у = 1 – 3х
11. Проверка 1вариант 2 вариант
ПРОВЕРКА1ВАРИАНТ
а)
2 ВАРИАНТ
а)
12. Проверка 1вариант 2 вариант
ПРОВЕРКА1ВАРИАНТ
б)
2 ВАРИАНТ
б)
13.
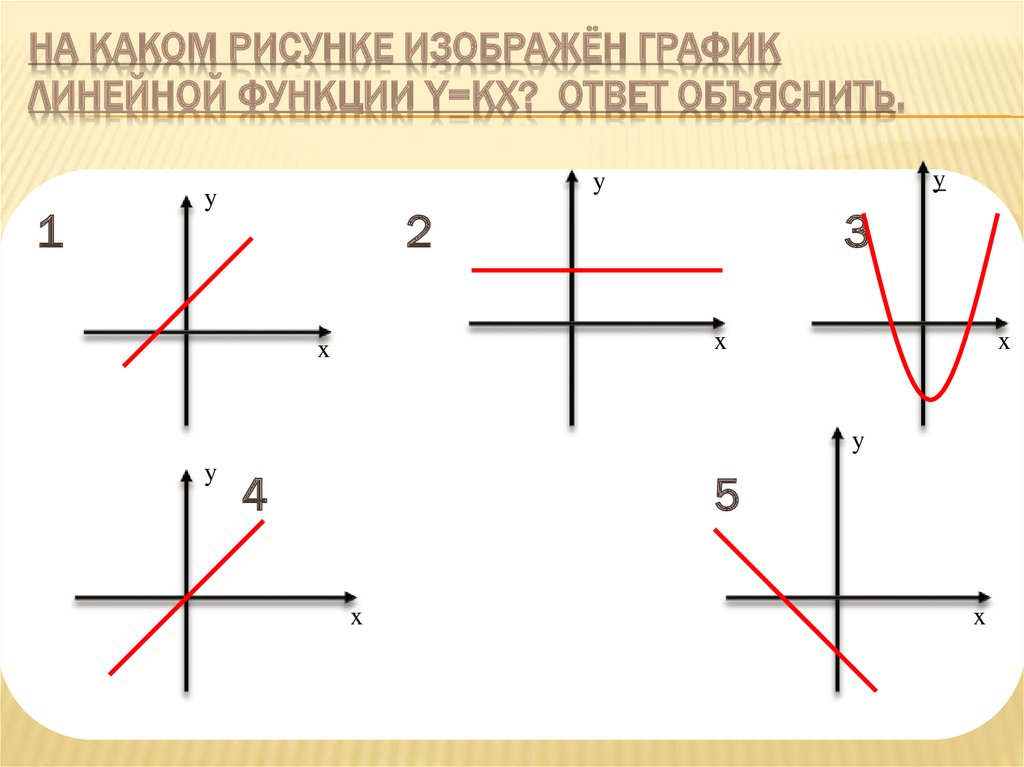
14. На каком рисунке изображён график линейной функции y=kx? Ответ объяснить.
НА КАКОМ РИСУНКЕ ИЗОБРАЖЁН ГРАФИКЛИНЕЙНОЙ ФУНКЦИИ Y=KX? ОТВЕТ ОБЪЯСНИТЬ.
1
y
y
y
2
3
x
x
x
y
y
4
5
x
x
15. Суворовец допустил ошибку при построении графика функции. На каком рисунке?
СУВОРОВЕЦ ДОПУСТИЛ ОШИБКУ ПРИПОСТРОЕНИИ ГРАФИКА ФУНКЦИИ. НА КАКОМ
РИСУНКЕ?
1. y=х+2
2. y=1,5х
3. y=-х-1
y
y
y
3
3
2
1
x
1
x
3x
16.
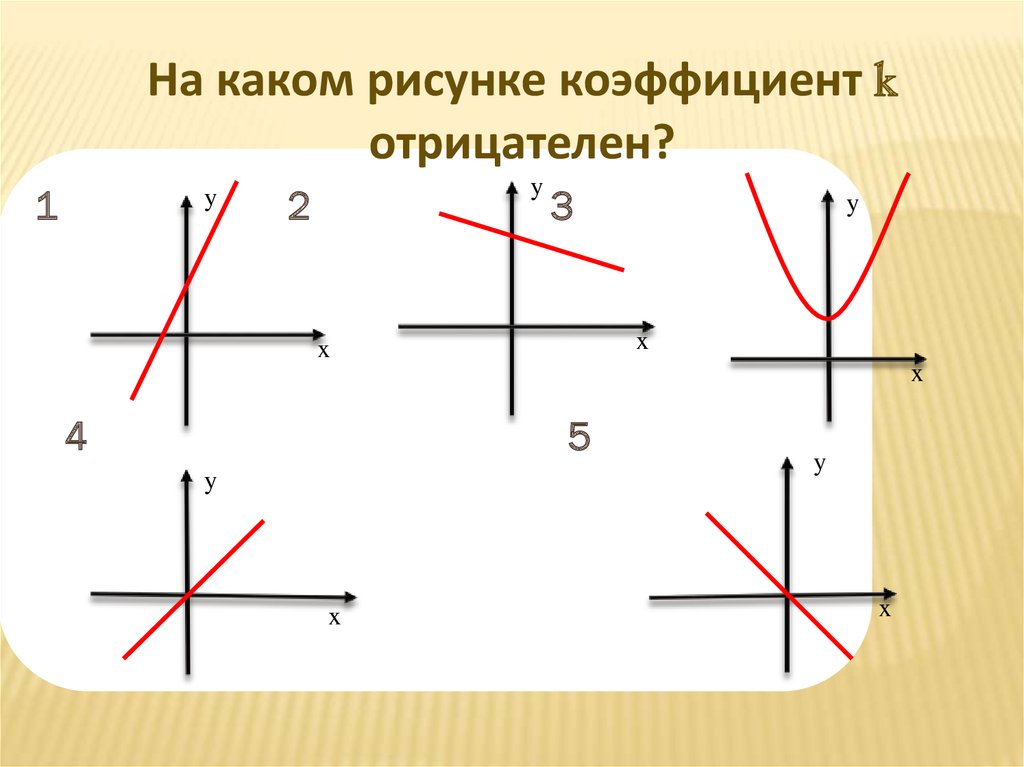
На каком рисунке коэффициент kотрицателен?
1
y
y
2
3
y
x
x
x
4
5
y
x
y
x
17.
3.Назовите знак коэффициента k для каждой из
линейных функций:
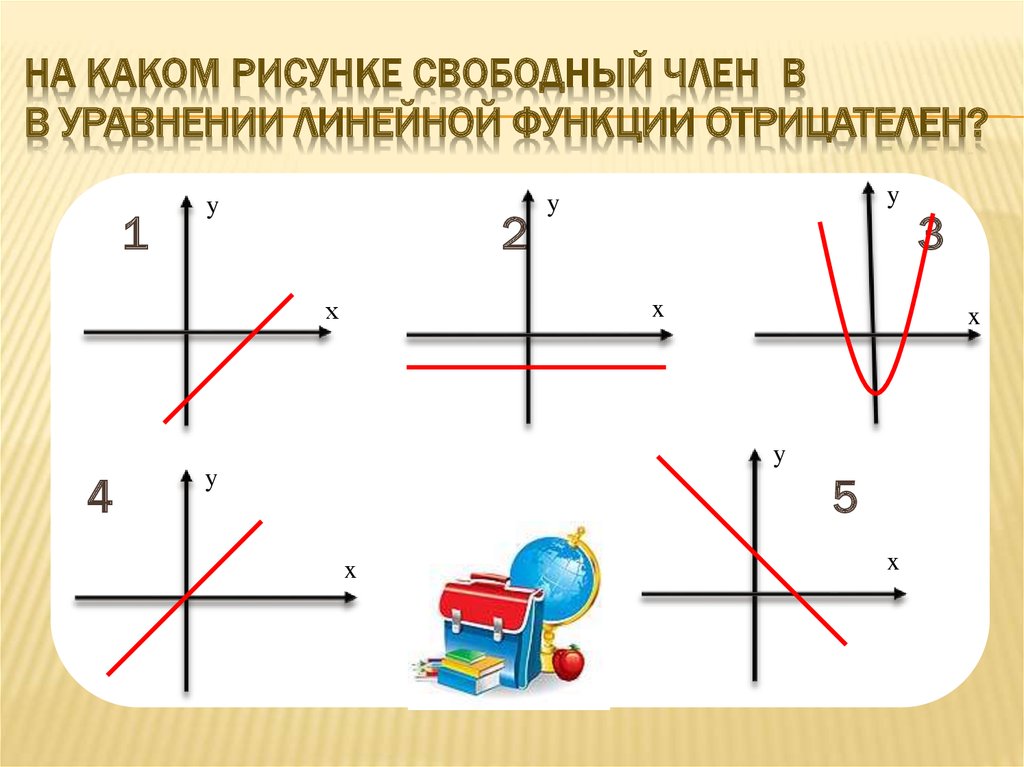
18. На каком рисунке свободный член b в уравнении линейной функции отрицателен?
НА КАКОМ РИСУНКЕ СВОБОДНЫЙ ЧЛЕН BВ УРАВНЕНИИ ЛИНЕЙНОЙ ФУНКЦИИ ОТРИЦАТЕЛЕН?
1
y
2
х
y
y
x
x
y
4
y
5
x
3
x
19.
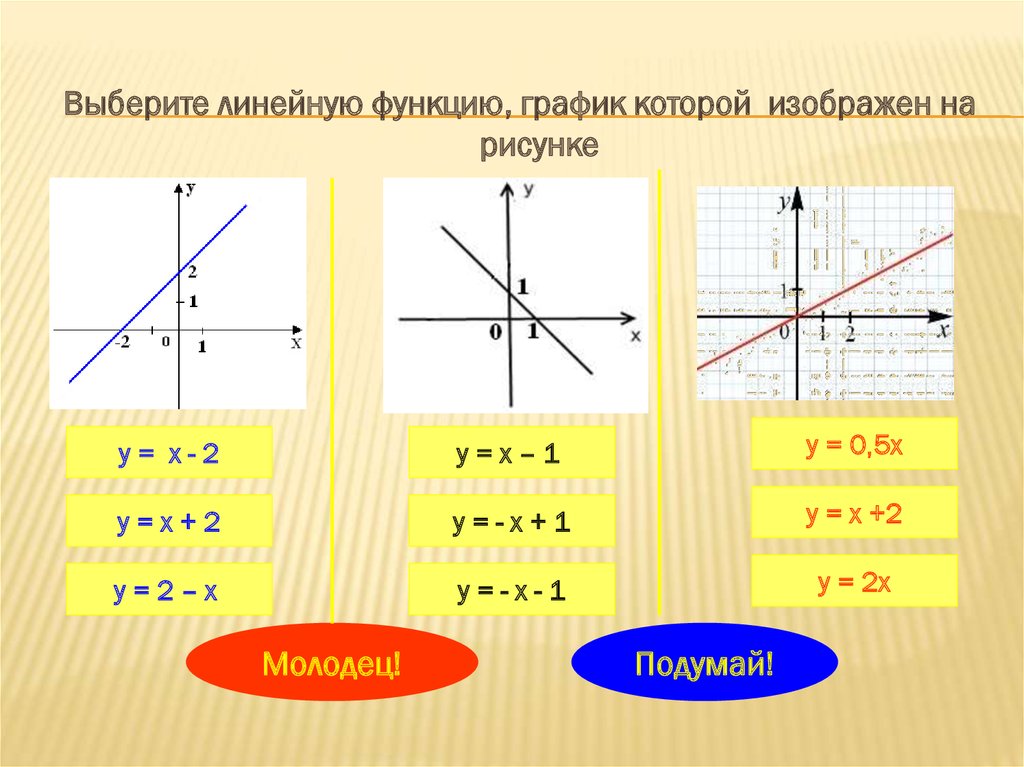
Выберите линейную функцию, график которой изображен нарисунке
у= х-2
у=х–1
у = 0,5х
у=х+2
у=-х+1
у = х +2
у=2–х
у=-х-1
у = 2х
Молодец!
Подумай!
20.
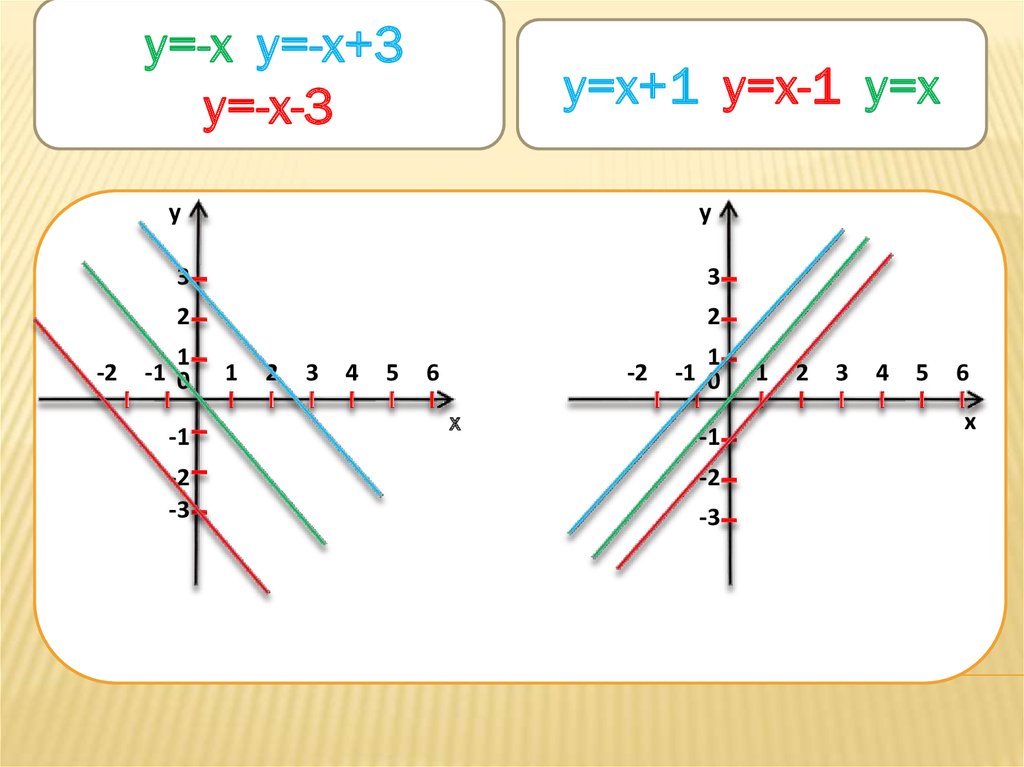
y=-x y=-x+3y=-x-3
Y=X+1
Y=X-1 y=x
,Y=X
y=x+1 y=x-1
y
-2
y
3
3
2
2
1
-1 0
-1
-2
-3
1
2
3
4
5
6
-2
x
1
-1 0
-1
-2
-3
1
2
3
4
5
6
x
21. Итог урока: *Функция вида у = kx + b называется линейной. *Графиком функции вида у = kx + b является прямая. *Для построения
ИТОГ УРОКА:*ФУНКЦИЯ ВИДА У = KX + B НАЗЫВАЕТСЯ ЛИНЕЙНОЙ.
*ГРАФИКОМ ФУНКЦИИ ВИДА У = KX + B ЯВЛЯЕТСЯ
ПРЯМАЯ.
*ДЛЯ ПОСТРОЕНИЯ ПРЯМОЙ НЕОБХОДИМЫ ТОЛЬКО
ДВЕ ТОЧКИ, ТАК КАК ЧЕРЕЗ ДВЕ ТОЧКИ ПРОХОДИТ
ЕДИНСТВЕННАЯ ПРЯМАЯ.
*КОЭФФИЦИЕНТ K ПОКАЗЫВАЕТ ВОЗРАСТАЕТ ИЛИ
УБЫВАЕТ ПРЯМАЯ.
*КОЭФФИЦИЕНТ B ПОКАЗЫВАЕТ, В КАКОЙ ТОЧКЕ
ПРЯМАЯ ПЕРЕСЕКАЕТ ОСЬ OY.
*УСЛОВИЕ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ.
22. Задание на самоподготовку
ЗАДАНИЕ НА САМОПОДГОТОВКУЗаписать алгоритм в словарь
А - № 8.18, 8.20, 8.23 (все а, б)
В - № 8.28.
23.
24. Готфрид Лейбниц – немецкий математик (1646 – 1716г.г.), который первым ввёл термин «абсцисса» - в 1695г., «ордината» - в
ГОТФРИД ЛЕЙБНИЦ –НЕМЕЦКИЙ
МАТЕМАТИК (1646 –
1716Г.Г.), КОТОРЫЙ
ПЕРВЫМ ВВЁЛ ТЕРМИН
«АБСЦИССА» - В 1695Г.,
«ОРДИНАТА» - В 1684Г.,
«КООРДИНАТЫ» - В
1692Г.
25. Рене Декарт – французский философ и математик (1596 – 1650г.г.), который первым ввёл понятие «функция»
РЕНЕ ДЕКАРТ –ФРАНЦУЗСКИЙ
ФИЛОСОФ И
МАТЕМАТИК (1596 –
1650Г.Г.), КОТОРЫЙ
ПЕРВЫМ ВВЁЛ
ПОНЯТИЕ «ФУНКЦИЯ»













 Математика
Математика








