Похожие презентации:
Симметрия фигуры
1.
«Симметрия является той идеей, посредством которойчеловек на протяжении веков пытался постичь и создать
порядок, красоту и совершенство».
Герман Вейль
2.
Симметрия фигуры – преобразование, переводящеефигуру в себя, т.е. обеспечивающее ее самосовмещение
Слово "симметрия" (symmetria) происходит от
греческого «сим»- с, вместе и «метрон»- мера.
Оно означает соразмерность, одинаковость,
наличие определенного порядка в расположении
частей чего-либо относительно точки, прямой,
плоскости.
3.
В математике рассматривается различные видысимметрии: осевая, зеркальная, центральная и
др.
Осевая симметрия –преобразование, при котором
каждая точка Е фигуры преобразуется в
симметричную ей относительно некоторой оси m
точку Е‘, при этом ЕЕ'┴m
А
О
А'
4.
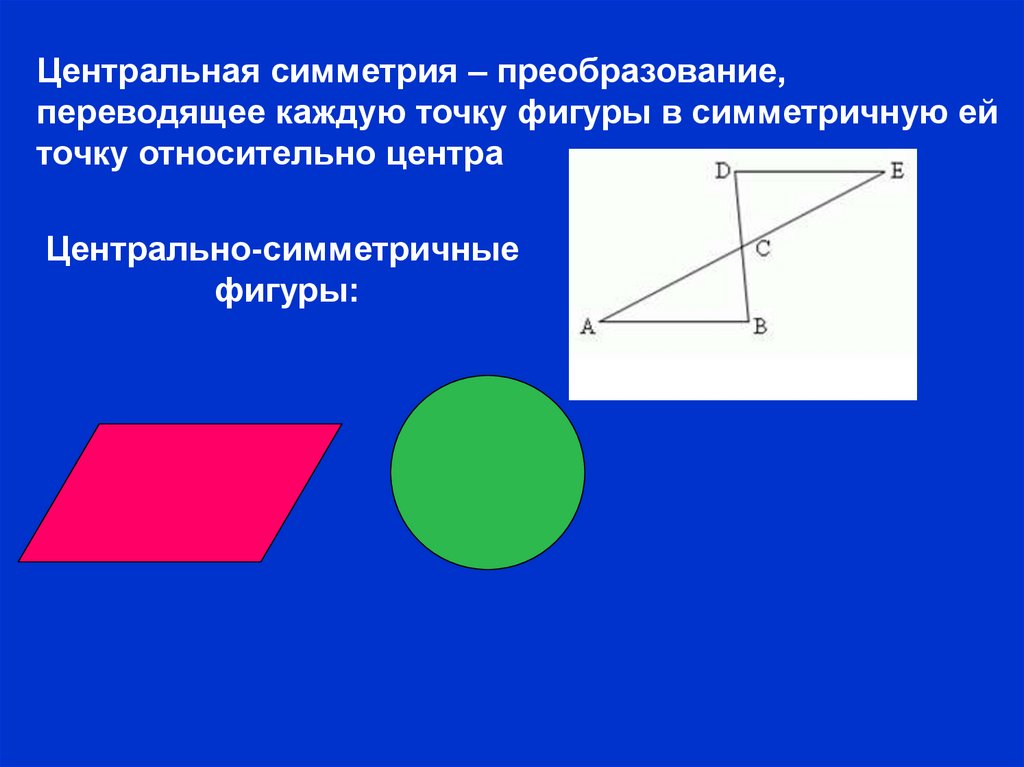
Центральная симметрия – преобразование,переводящее каждую точку фигуры в симметричную ей
точку относительно центра
Центрально-симметричные
фигуры:
5.
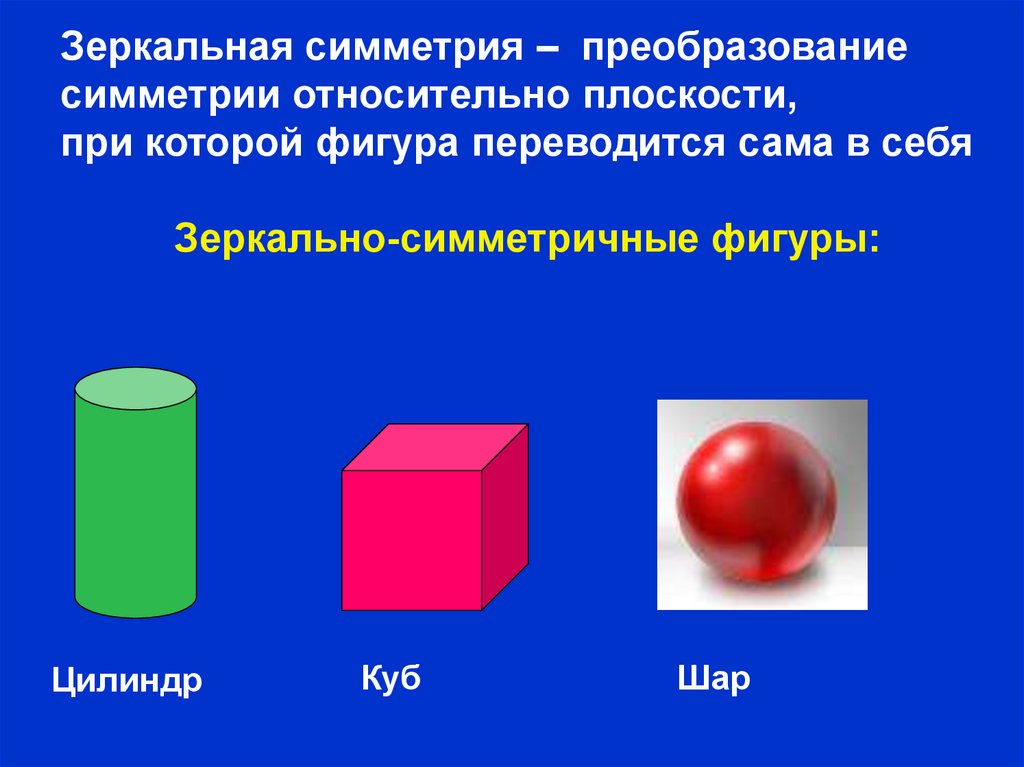
Зеркальная симметрия – преобразованиесимметрии относительно плоскости,
при которой фигура переводится сама в себя
Зеркально-симметричные фигуры:
Цилиндр
Куб
Шар
6.
С симметрией мы встречаемся везде – в природе, технике,науке, искусстве. Понятие симметрии проходит через всю
многовековую историю человеческого творчества. Симметрия
буквально пронизывает весь окружающий нас мир. Принципы
симметрии играют важную роль в физике, математике, биологии,
химии, технике, архитектуре, поэзии, музыке.
7.
«На Земле жизнь зародилась в сферически симметричных формах,а потом стала развиваться по двум главным линиям: образовался мир
растений , обладающих симметрией конуса, и мир животных с
билатеральной симметрией.» М.Гарднер
В основе строения любой живой формы лежит принцип
симметрии. Для растений характерна симметрия конуса, для
цветов – поворотная симметрия. Часто поворотная симметрия
сочетается с зеркальной или переносной.
Симметрия конуса
Поворотная симметрия
Поворотная в сочетании
с зеркальной
8.
Для представителей животного мирахарактерна зеркальная симметрия
9.
10.
Если прогуляться по древним городам, токрасота древних зданий вызывает
невольное восхищение.
11.
«Кристаллы блещут симметрией» Е.С.ФедоровКристаллы вносят в мир неживой природы очарование симметрии,
то есть свойством совмещаться с собой в различных положениях
путем поворота, параллельного переноса. Каждая снежинка – это
маленький кристалл замершей воды. Форма снежинок
разнообразна, но все они обладают симметрией.
12.
«Математик, так же как художник или поэт, создает узоры»Г.Харди
Принцип симметрии используется в построении орнамента.
Орнамент – узор, состоящий из повторяющихся, ритмически
упорядоченных элементов. Для русского орнамента характерны
как геометрические и растительные формы, так и изображения
птиц, зверей, фантастических животных. Наиболее русский
орнамент выражен в резьбе по дереву и вышивке.
13.
1. Сколько осей симметрии имеют буквы: А,Д,М,П,Ф?а) 1 б) 2 в)3 г) ни одной
2. Сколько осей симметрии имеют буквы: В, Е, З,С?
а)2 б) 1 в) 3 г) ни одной
3.Сколько осей симметрии имеют буквы: Ж, Н,О,Х?
а)1 б)2 в)3 г) ни одной
4.Сколько осей симметрии имеют буквы: Б,Г,Й,Р?
а)1 б)2 в)4 г) ни одной
5. Сколько осей симметрии имеет равносторонний
треугольник?
а)1 б)2 в)3 г)4
6.Сколько осей симметрии имеет прямоугольник?
а)1 б)2 в)3 г)4
14.
1.Л.С.Сагатеева, В.Н.Студенецкая «Геометрия:красотаи гармония»
2.Энциклопедический словарь юного математика
3.М.В.Величко «Проектная деятельность учащихся»
Презентацию подготовила учитель математики
Лоскутова Вера Александровна












 Математика
Математика








