Квантовая физика. Квантование момента импульса

1.

Физика. 2 курс. 4 семестр
Специалитет
Лекция 5. Квантовая физика
Квантование момента импульса
Ротатор
В.И. Читайкин
кандидат физико-математических наук
доцент

2.

План лекции
Наименование раздела, параграфа
Номер слайда
Введение
3
Раздел 1. Квантование момента импульса
4
1.1. Основные понятия
5
1.2. Квантование модуля момента импульса М
6
1.3. Квантование проекции момента импульса Мz
7
1.4. Связь орбитального l и магнитного m чисел
8
Раздел 2. Ротатор
9
2.1. Основные понятия
10
2.2. Свойства ротатора
12
2.3. Вращательный спектр
13
2.4. Колебательно-вращательный спектр
14
Замечание
15
2

3.

Введение
В 5-ой лекции, в разделе 1 рассматривается квантование ещё одной физической величины:
момента импульса частицы М и его проекции на одну ось МZ. В предыдущих лекциях изучалось
квантование полной энергии Е и, значит, импульса частицы р (напомню: E = p2 / 2m). За это
«отвечает» главное квантовое число n.
Значения n есть: 1, 2, 3, … для одних потенциалов (вспомните – каких?); и 0, 1, 2, 3, …для других потенциалов
(вспомните – каких?).
В разделе 2 лекции рассматривается физическое понятие ротатор (от слова вращение), тесно
связанное с понятием момента импульса. Также выполняется его квантование, т.е. определение
дискретных уровней.
Вращательные уровни ротаторов, как и колебательные уровни осцилляторов (см. предыдущие
лекции) «работают» совместно в реальных частицах (молекулах). Эти понятия позволяют разобраться
в запутанных спектрах возбуждения / поглощения молекул, наблюдаемых в экспериментах.
Следует помнить, что понятия «колебание» и «вращение» носят условный характер, т.к. в
квантовой физике наглядных образов используемых понятий практически нет.
Рассмотрение вопросов в лекции ведётся, по-прежнему, для стационарных условий.
Этой лекцией завершается курс «Основы квантовой физики», результаты которого будут активно
использоваться в последующих разделах.
3

4.

Раздел 1. Квантование момента импульса
4

5.

1. Квантование момента импульса
1.1. Основные понятия
Рассматривается 3D-пространство.
В классической физике: момент импульса – это вектор М = [r∙p] ([…] – векторное произведение).
Величина (модуль) и направление вектора М и величины (модули) его трёх проекций на оси МX, MY,
MZ точно известны и сохраняются в изолированной системе. Это ещё один закон сохранения в
классической физике.
Строго говоря, момент импульса – это псевдо-вектор, т.е. он прикладывается к центру
окружности, по которой движется частица, а не к самой частице – см. рисунок.
В квантовой физике: в силу соотношения неопределённостей Гейзенберга,
могут быть точно известны значения только модуля момента импульса
М = modM и только одна проекция вектора М, например, Mz, остальные
проекции являются полностью неопределенными. Подумайте, почему?
Наглядный образ: Вектор М как бы «размазан» по образующей конуса, значения его
проекций MX и MY оказываются полностью неопределёнными, т.е. могут принимать любые
значения вдоль окружности, расположенной в плоскости XY.
Конечно, этот наглядный образ условен, как всегда в квантовой физике.
Закон сохранения момента импульса в квантовой физике «не работает».
МZ
М
Y
Х
Почему вектор М не перпендикулярен
плоскости вращения частицы?
Замечание.
Часто момент импульса и его проекции обозначают буквами L и LX, LY, LZ, соответственно.
5

6.

1. Квантование момента импульса
Предварительное замечание. Каждая из точно известных величин: модуль момента импульса М и его
проекция МZ, – могут быть «проквантованы». О квантовании остальных проекций: МX, MY , – в силу их
неопределённости, говорить не приходится. Рассмотрим последовательно результаты квантования М и МZ.
1.2. Квантование модуля момента импульса М
Последовательный математический анализ решения 3D-уравнения Шредингера в сферических
координатах (мы опустим его из-за чрезмерной громоздкости) показывает, что собственные значения модуля
момента импульса являются дискретными (квантованными).
М2
l = 0, 1, 2, 3 … - орбитальное квантовое число
М
Приведены решение для М2 и М и соответствующие значения l в случае атома (т.е. для
для электрона в центрально-симметричном потенциале ядра), как наиболее практически
важном.
Подчеркну вновь: дискретность физической величины – модуля момента импульса М – была
получена (обнаружена) в результате решения дифференциального уравнения Шредингера, т.е. чисто
математическим способом.
6

7.

1. Квантование момента импульса
1.3. Квантование проекции момента импульса МZ
Из результатов операторного анализа уравнения Шредингера (см. замечание в конце лекции) следует, что для
определения собственных дискретных значений проекции момента импульса Мz надо решить уравнение,
записанное в сферической системе координат:
MZ ∙ψ(φ)
φ – угол в плоскости XY – см. рисунок на предыдущем слайде.
Значение φ изменяется, очевидно, от 0 до 2π.
Решение этого уравнения: = С∙exp(imφ) , где m = МZ /ℏ
Проверьте прямой подстановкой
Функция ψ(φ) должна быть конечной, непрерывной, гладкой; а также периодической (синусоидального
типа), чтобы было выполнено условие однозначности.
Тогда: ψ(φ + 2π) = ψ(φ). Отсюда следует, что параметр m должен быть целочисленным, т.е. волновая
функция ψ(φ) должна быть дискретной (квантованной).
Легко видеть, что проекция момента импульса кратна постоянной Планка:
МZ = mℏ = m∙(h/2π)
m = 0, ±1, ±2, ±3 …
Определение: число m называется магнитным квантовым числом.
Замечание: дискретность физической величины – проекции момента импульса на ось Z, т.е. МZ – была
вновь получена (обнаружена) чисто математическим способом.
7

8.

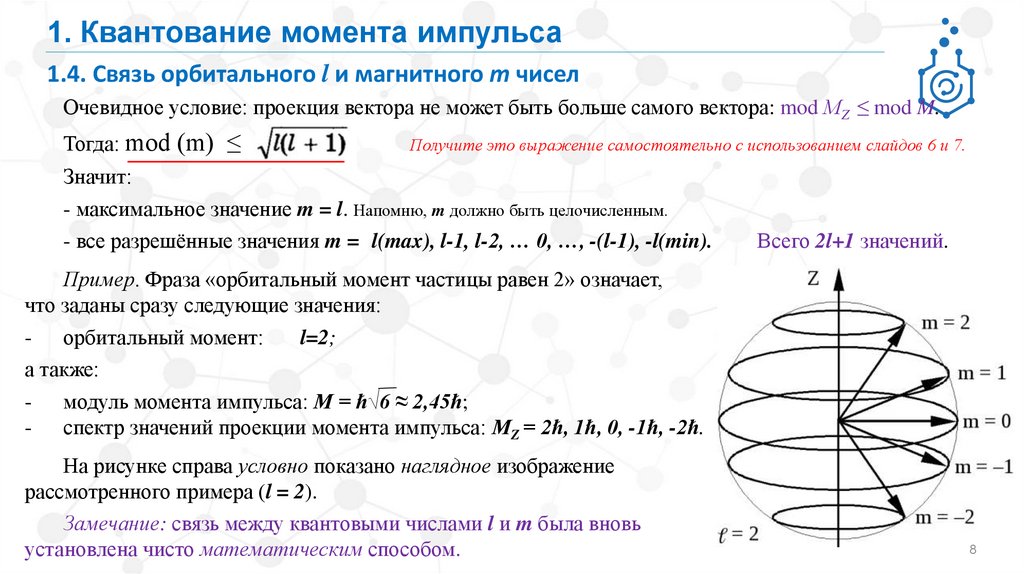
1. Квантование момента импульса
1.4. Связь орбитального l и магнитного m чисел
Очевидное условие: проекция вектора не может быть больше самого вектора: mod МZ ≤ mod M.
Тогда: mod (m) ≤
Получите это выражение самостоятельно с использованием слайдов 6 и 7.
Значит:
- максимальное значение m = l. Напомню, m должно быть целочисленным.
- все разрешённые значения m = l(max), l-1, l-2, … 0, …, -(l-1), -l(min).
Всего 2l+1 значений.
Пример. Фраза «орбитальный момент частицы равен 2» означает,
что заданы сразу следующие значения:
- орбитальный момент:
l=2;
а также:
- модуль момента импульса: М = ℏ√6 ≈ 2,45ℏ;
- спектр значений проекции момента импульса: МZ = 2ℏ, 1ℏ, 0, -1ℏ, -2ℏ.
На рисунке справа условно показано наглядное изображение
рассмотренного примера (l = 2).
Замечание: связь между квантовыми числами l и m была вновь
установлена чисто математическим способом.
8

9.

Раздел 2. Ротатор
9

10.

2. Ротатор
2.1. Основные понятия
Определение: Ротатор – это неизменяемая вращательная система (твёрдое тело).
В классической механике: кинетическая энергия вращающегося твёрдого тела (ротатора):
Е = М2 /2I,
где М – момент импульса,
I – момент инерции тела относительно выбранной оси вращения.
Опуская громоздкие вычисления, опираясь на физическую интуицию и классическую аналогию, можно
записать формулу для собственных значений вращательной энергии квантово-механической частицы:
l = 0, 1, 2, 3, …
Самостоятельно получите это выражение, используя ранее
полученную формулу для момента импульса (см. сл.6),
Иногда обозначение квантового числа l для ротатора заменяют на обозначение r (rotaion) и,
соответственно, El на Er. Например, так сделано в учебнике И.Е.Иродова. Это – формальное
переобозначение, чтобы подчеркнуть, что формула имеет отношение к вращению. Тогда число r называется
вращательным квантовым числом.
Главное: энергия вращательного движения также квантуется, т.е. дискретна, как и полная энергия или
энергия осциллятора (см. предыдущие лекции).
10

11.

2. Ротатор
2.1. Основные понятия (продолжение)
В задачнике Чертова и в ряде учебников по квантовой физике используются иные обозначения.
Орбитальное квантовое число l обозначается как J.
Вводится новый параметр – вращательная постоянная В = ℏ2/2I
I – момент инерции.
Размерность [B] – Дж.
С учётом этих переобозначений формула для собственных значений вращательной энергии квантовомеханической частицы записывается так:
Евр = В∙J(J + 1).
Или, что то же самое:
Евр =
.
Важные следствия для вращательного энергетического спектра:
1). Евр ~ l2.
2). Еmin = E(l=0) = 0.
Сравните с ангармоническим осциллятором.
11

12.

2. Ротатор
2.2. Свойства ротатора
1. Энергетический зазор, т.е. расстояние между соседними вращательными уровнями ΔЕ
увеличивается с ростом числа l (или r – иное обозначение):
ΔЕ = El+1 – El = (ℏ2/I)∙(l + 1),
получите самостоятельно
т.е.
ΔЕ ~ l.
На рисунке справа условно показаны вращательные уровни. Энергетический
спектр ротатора по мере роста энергии Е становится более разреженным.
Напомню, для осциллятора ситуация иная:
- колебательные уровни гармонического осциллятора эквидистантны;
- колебательные уровни ангармонического осциллятора сгущаются по мере роста Е.
Энергия излучения между вращательными уровнями: ΔЕ = ℏω,
значит, частота вращательного спектра: ω = (ℏ/I)∙(l + 1),
т.е. ω ~ l, – частота растёт с ростом квантового числа l, как и ширина
энергетического зазора ΔЕ.
2. Для перехода между вращательными уровнями действует уже знакомое правило отбора:
Δl = ± 1, т.е. вращательное квантовое число может меняться только единицу.
Обратите внимание: переход с Δl = 0 запрещён!
12

13.

2. Ротатор
2.3. Вращательный спектр
Собственно вращательный спектр – это совокупность частотных линий ω, обусловленных
переходами между вращательными энергетическими уровнями El.
l
Еl
4
ω4
3
ω3
2
ω1
ω2
Δω
Δω
1
0
Δω
Нетрудно видеть, что, несмотря на неэквидистантность
энергетического спектра (верхний рисунок), линии
частотного спектра (нижний рисунок) отстоят
друг от друга на одну и ту же величину Δω = ℏ/I.
Покажите это самостоятельно. Подсказка: обратите внимание, что в формуле
использовано выражение Δω, а не ω.
ω1
ω2
ω3
ω4 ω
13

14.

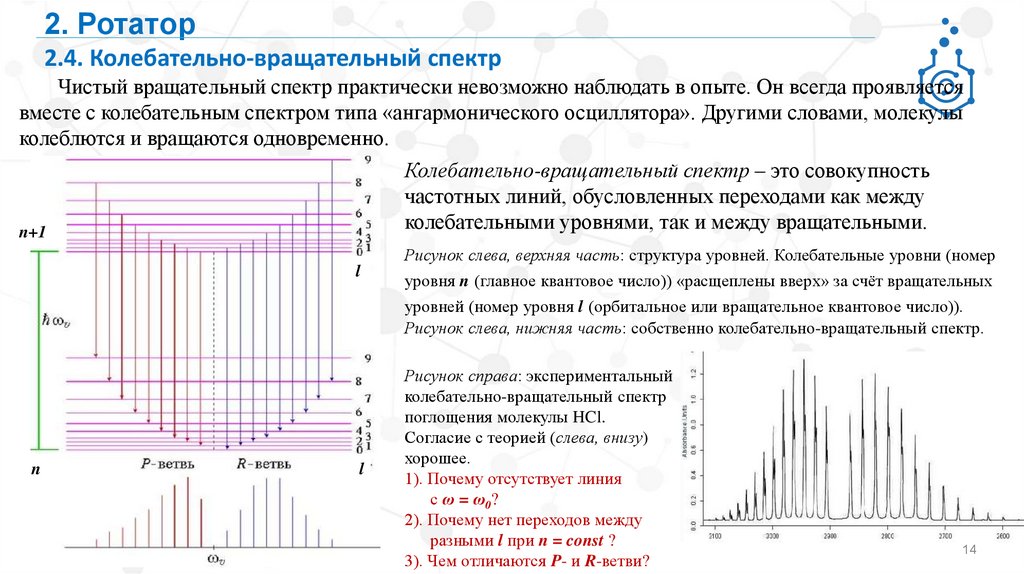
2. Ротатор
2.4. Колебательно-вращательный спектр
Чистый вращательный спектр практически невозможно наблюдать в опыте. Он всегда проявляется
вместе с колебательным спектром типа «ангармонического осциллятора». Другими словами, молекулы
колеблются и вращаются одновременно.
Колебательно-вращательный спектр – это совокупность
частотных линий, обусловленных переходами как между
колебательными уровнями, так и между вращательными.
n+1
Рисунок слева, верхняя часть: структура уровней. Колебательные уровни (номер
l
уровня n (главное квантовое число)) «расщеплены вверх» за счёт вращательных
уровней (номер уровня l (орбитальное или вращательное квантовое число)).
Рисунок слева, нижняя часть: собственно колебательно-вращательный спектр.
n
l
Рисунок справа: экспериментальный
колебательно-вращательный спектр
поглощения молекулы HCl.
Согласие с теорией (слева, внизу)
хорошее.
1). Почему отсутствует линия
с ω = ω0?
2). Почему нет переходов между
разными l при n = const ?
3). Чем отличаются P- и R-ветви?
14

15.

Замечание
В этой и предыдущих лекциях не используется операторный анализ. Это, конечно, немного
обедняет изложение, но, вместе с тем, делает его чуть более физичным.
С основами операторного анализа в преломлении к квантовой физике можно ознакомиться в
учебнике И.Е.Иродова «Квантовая физика. Основные законы», §5.1, §5.2.
15

16.

Спасибо за внимание