Метод опорных векторов

1.

Метод опорных векторов

2.

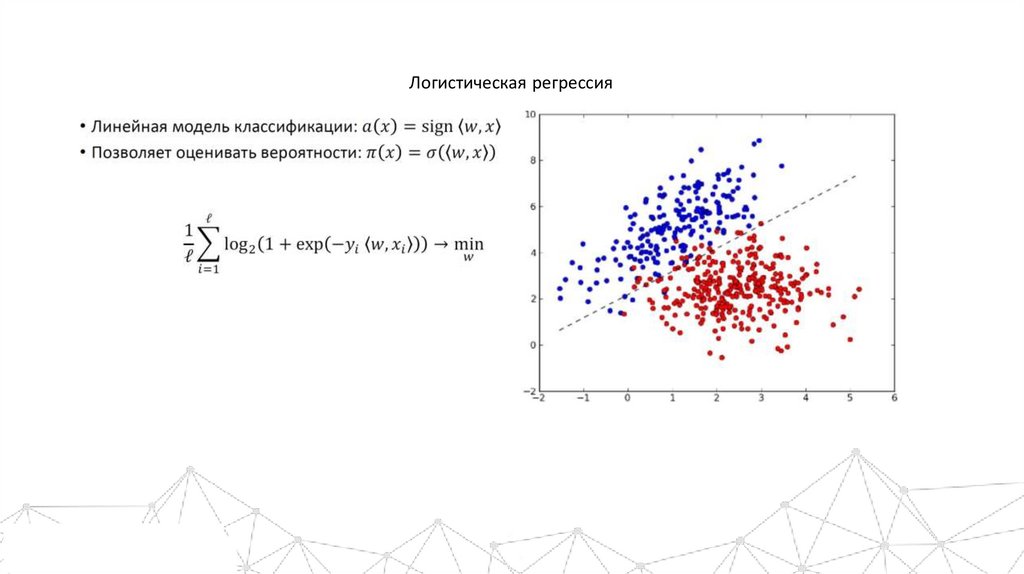
Логистическая регрессия

3.

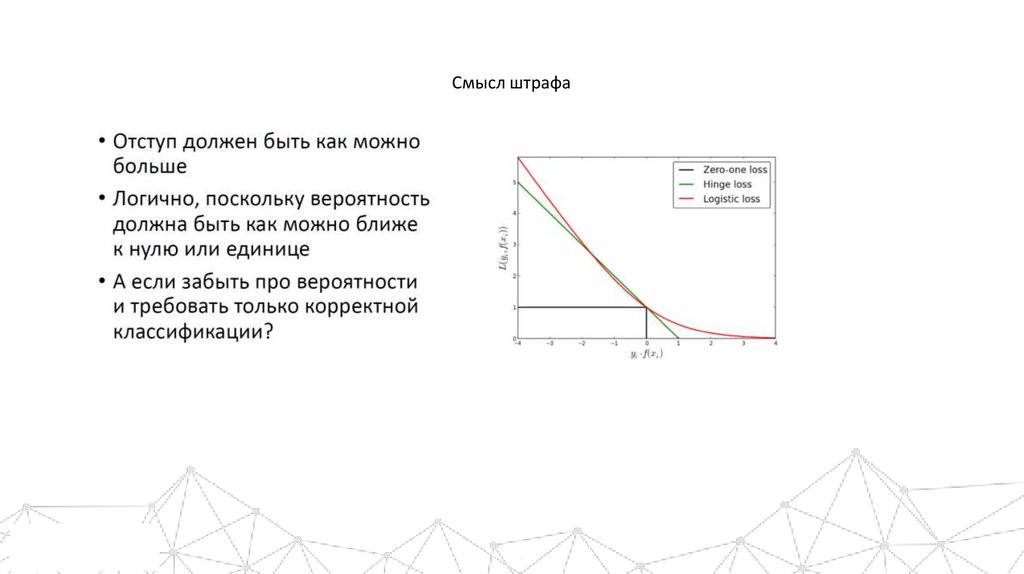
Смысл штрафа

4.

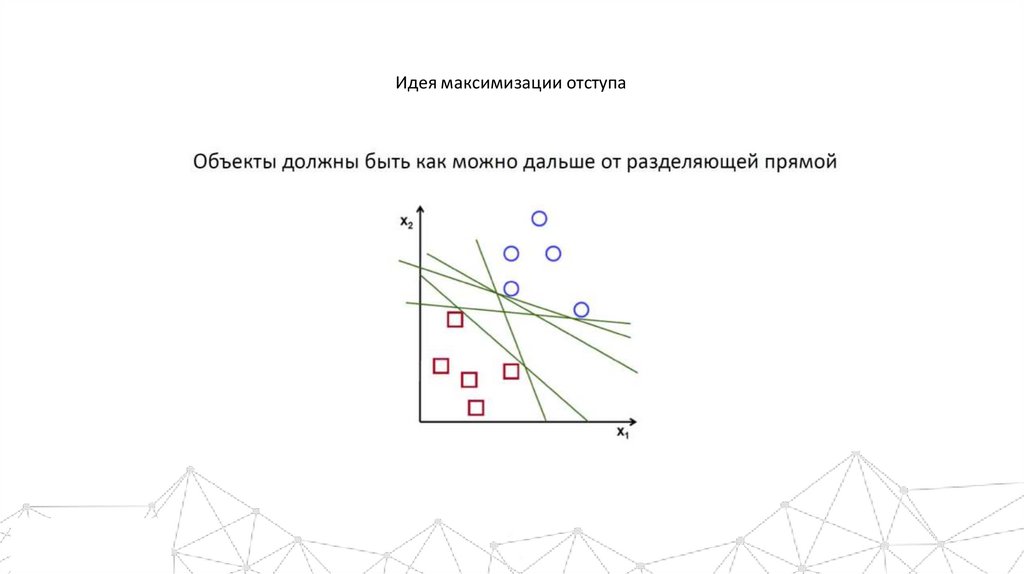
Идея максимизации отступа

5.

Идея максимизации отступа

6.

Идея максимизации отступа

7.

Геометрия линейного классификатора

8.

Идея максимизации отступа

9.

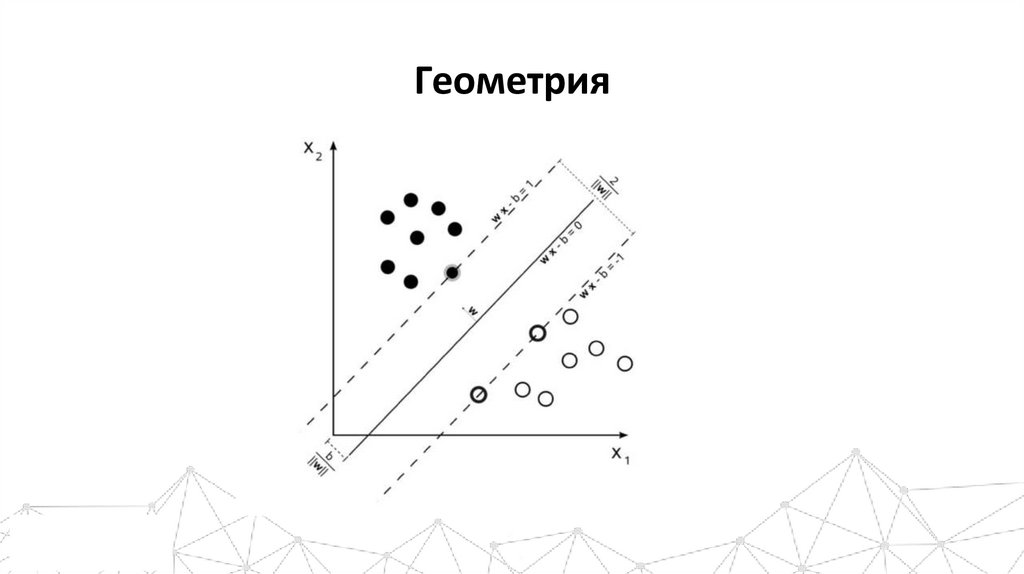
Геометрия

10.

Задача максимизации ширины полосы

11.

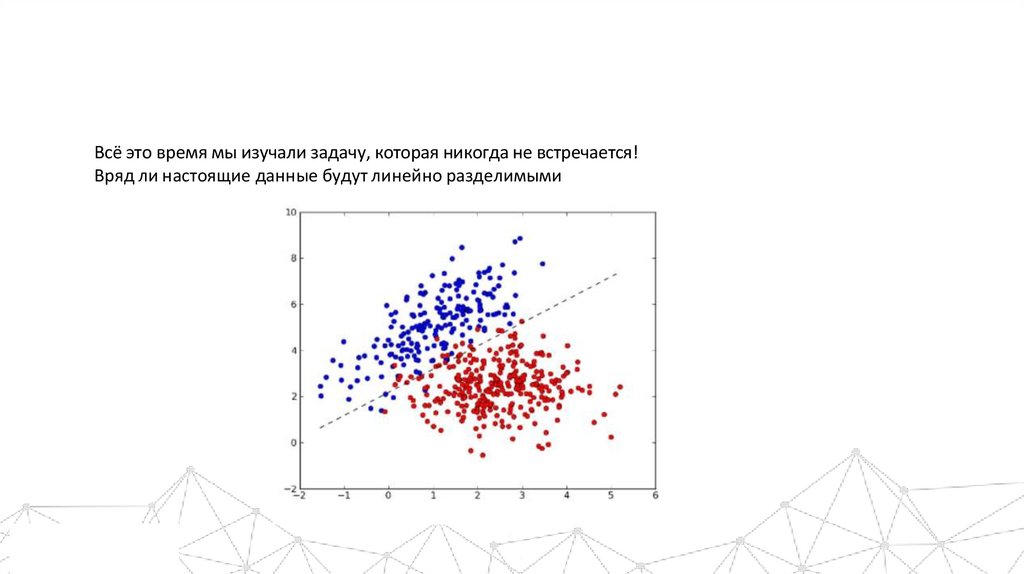
Всё это время мы изучали задачу, которая никогда не встречается!
Вряд ли настоящие данные будут линейно разделимыми

12.

Задача максимизации ширины полосы

13.

Задача максимизации ширины полосы

14.

Метод опорных векторов (SVM)

15.

Метод опорных векторов (SVM)

16.

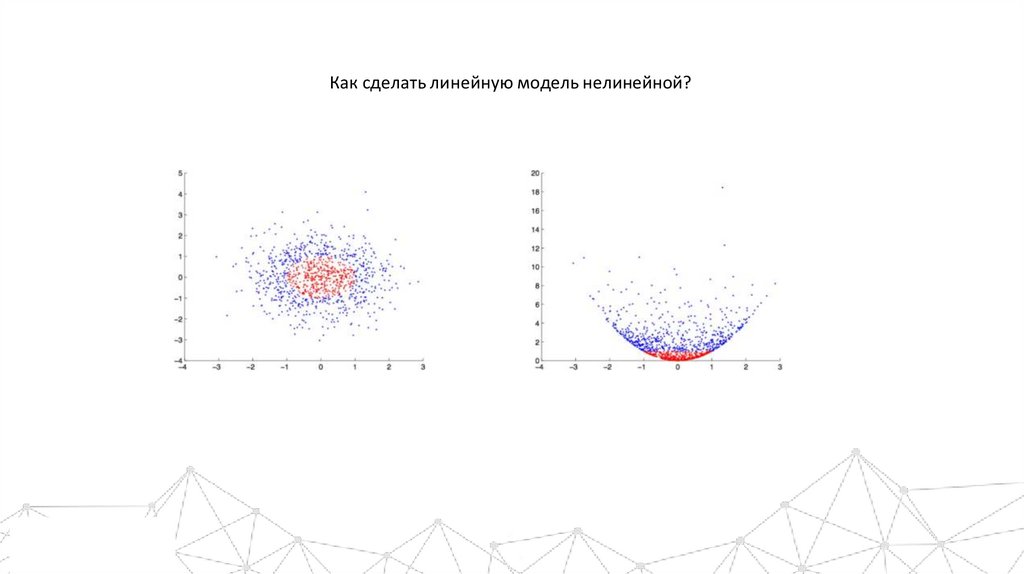
Как сделать линейную модель нелинейной?

17.

Нелинейные признаки

18.

19.

Двойственная задача

20.

Двойственная задача

21.

Двойственная задача

22.

Двойственная задача

23.

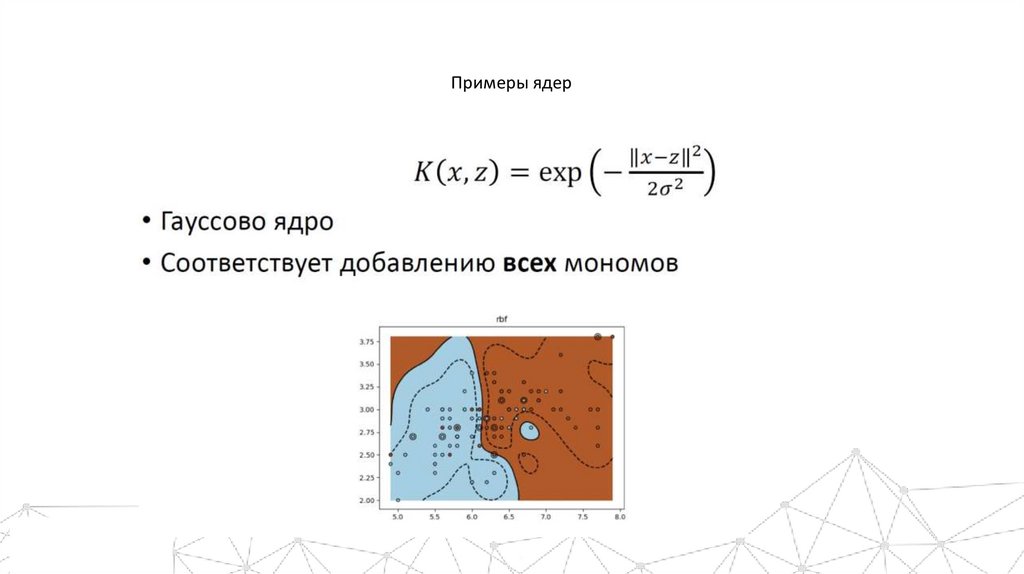
Примеры ядер

24.

Примеры ядер

25.

Метод опорных векторов (SVM)

26.

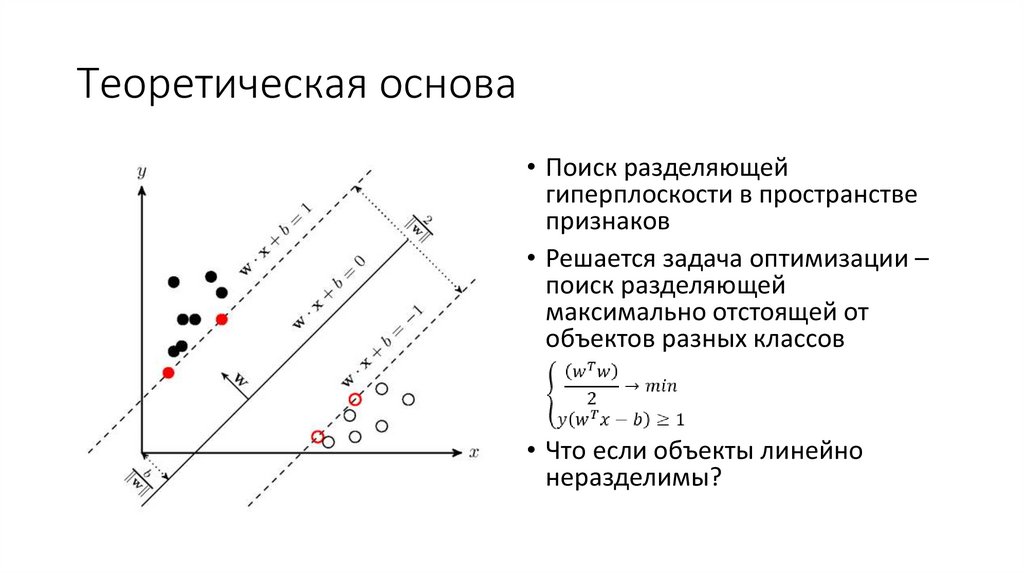
Теоретическая основа
• Поиск разделяющей
гиперплоскости в пространстве
признаков
• Решается задача оптимизации –
поиск разделяющей
максимально отстоящей от
объектов разных классов
• Что если объекты линейно
неразделимы?

27.

Введение функции ошибки
• Позволим нашей модели ошибаться.
• Введём понятие штрафа
• После этого можно построить функцию потерь и оптимизировать
её методом градиентного спуска

28.

Введение ядра
Заменяем скалярные произведения на функцию-ядро
• Наиболее популярные ядра:
• Полиномиальное (однородное): K x, x ′ = (x ∙ x′)