Метод координат и метод векторов при решении задач

1. Метод координат и метод векторов при решении задач

2. Цель:

Рассмотрение эффективных приемов
использования популярных методов
решения задач (векторного и
координатного)
Рассмотрение примеров решения
задач.

3. История

Пьер Ферма
Рено Декарт

4. Некоторые определения и вычислительные формулы

Координаты точки на прямой.
0 1 а
А
А(а)

5. Задачи на прямой в координатах

1. Вычисление длины отрезка АВ.
Дано: А(х1), В(х2).
Найти АВ.
Решение:

6. Задачи на прямой в координатах

2. Вычисление координаты середины отрезка.
Дано: А(х1), В(х2), С – середина отрезка АВ.
Найти координату С.
Решение:

7. Координаты точки на плоскости

Определение координат
точки методом проекций на оси.

8. Координаты точки на плоскости

Определение координат
точки через координаты
ее радиус-вектора.

9. Деление отрезка пополам.

Дано: А(х1, у1), В(х2, у2),С(х,
у) – середина отрезка АВ.
Найти координаты С.
Решение:

10. Расстояние между точками

Дано: А(х1, у1), В(х2, у2)
Найти АВ.
Решение:

11. Некоторые свойства векторов

Коллинеарность векторов
Первый признак:
Второй признак:

12. Некоторые свойства векторов

Вычисление координат вектора по
координатам его начала и конца.

13. Некоторые свойства векторов

Вычисление длины вектора и длины
отрезка

14. Некоторые свойства векторов

Скалярное произведение векторов в
прямоугольной системе координат

15. Некоторые свойства векторов

Признак перпендикулярности
векторов:
два ненулевых вектора
перпендикулярны тогда и только
тогда, когда их скалярное
произведение равно нулю.

16. Некоторые свойства векторов

Вычисление угла между векторами.

17. Некоторые свойства векторов

Вычисление площади
параллелограмма, построенного на
двух векторах.

18. Уравнения прямой и отрезка

Параметрические уравнения прямой.

19. Уравнения прямой и отрезка

Канонические уравнения прямой.

20. Уравнения прямой и отрезка

Общее уравнение прямой.

21. Уравнения прямой и отрезка

Условие перпендикулярности двух
прямых, заданных как графики
линейных функций.

22. Уравнение окружности

23. Примеры решения задач

Задача 1. Дана прямоугольная
трапеция с основаниями a и b.
Найдите расстояние между
серединами ее диагоналей.
Решение. 1. Введем систему координат как указано на рисунке 3. Тогда
вершины трапеции будут иметь координаты: A(0,0), B(0,y), C(b,y) и D(a,0).
(y – высота трапеции, АВ).
0 b b
0 y y
x
;
y
2. Найдем координаты середин
O
O
2
2
2
2
диагоналей. Для точки О,
0 a a
0 y y
x
;
y
O1
O1
для точки О1:
2
2
2
2
.По
формуле найдем расстояние между
точками О и О1:

24. Примеры решения задач

.
.
Примеры решения задач
Задача 2. Медиана, проведенная к основанию
равнобедренного
треугольника, равна 160 см, а основание
треугольника равно 80 см.
Найдите
две
другие
медианы
этого
треугольника.
Решение. 1. Введем прямоугольную систему
координат так, как показано на рисунке 4. В этой
системе вершины треугольника будут иметь
координаты:
А(-40,0), В(0, 160), С(40,0), а точка М2(0,0).
0 ( 40)
160 0
xM 3
20; yM 3
80
2
2
0 40
160 0
xM1
20; yM1
80
2
2
Вычислим длины отрезков АМ1 и СМ3, используя формулу (6). Для АМ1 получим:
AM1 (20 ( 40))2 (80 0)2 100 (см)
AM1 CM 3 100 (см)

25. Примеры решения задач

Задача 3. В прямоугольном
равнобедренном треугольнике
проведены медианы острых углов.
Вычислите косинус угла между ними.
Решение. 1. Введем систему координат так, как
показано на рисунке 5. В этом случае Вершины
треугольника будут иметь координаты: С(0,0), А(а,0),
В(0,а), а середины катетов (Здесь а – длина катета.):
a a
B1 , 0 ; A1 0,
2 2
2. По формуле (4) вычислим координаты векторов
a
a
AA1 0 a; 0 a;
2
2
cos AA1 , BB1
a
a
BB1 0;0 a ; a
2
2
a a
( a) ( a)
2 2
2
2
a
a
( a) ( a) 2
2
2
2
4
5

26. Метод координат в пространстве

МЕТОД КООРДИНАТ В
ПРОСТРАНСТВЕ

27. Основные формулы

Координаты вектора по координатам его начала и
конца определяются так: если М1(x1,y1,z1),
M2 (x2, y2, z2), то
= (x2 – x1, y2 – y1, z2 – z1)

28. Основные формулы

Скалярное произведение векторов = (а1, а2, а3) и =
(b1, b2, b3) в координатах равно:
a b = a1 b1 + a2 b2 + a3 b3

29. Основные формулы

Длина вектора = (а1, а2, а3)
вычисляется по формуле

30. Основные формулы

Угол между векторами = (а1, а2, а3) и =
(b1, b2, b3) из определения скалярного
произведения
a b = a b cos( a , b )

31. Основные формулы

Угол между векторами = (а1, а2, а3) и =
(b1, b2, b3) из определения скалярного
произведения
=
=

32. Основные формулы

Расстояние между двумя различными
точками М1(x1,y1,z1) и M2 (x2, y2, z2)
равно
=
=

33. Основные формулы

Уравнение сферы с центром в точке
С(x0,y0,z0) и радиусом r имеет вид:
(x – x0)2 + (y – y0)2 + (z – z0)2 = r2

34. Основные формулы

Координаты точки М(x,y,z) – середины отрезка
М1М2, где М1(x1,y1,z1) и
M2 (x2, y2, z2), М1 ≠ М2 находятся по формулам:

35. Основные формулы

Условие коллинеарности векторов =
(а1, а2, а3) и = (b1, b2, b3) имеет вид

36. Примеры решения задач

Задача
1.
R 0, i , j , k
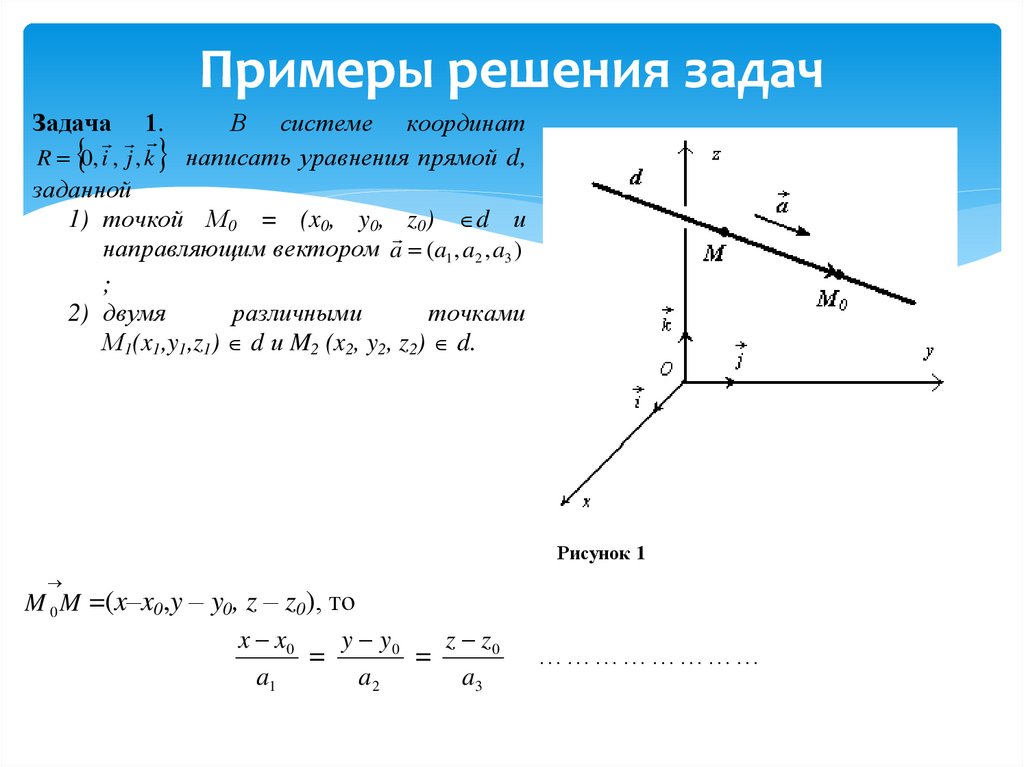
В системе координат
написать уравнения прямой d,
заданной
1) точкой М0 = (x0, y0, z0) d и
направляющим вектором a (a1 , a2 , a3 )
;
2) двумя
различными
точками
М1(x1,y1,z1) d и M2 (x2, y2, z2) d.
Рисунок 1
M 0 M =(x–x0,y – y0, z – z0), то
y y0
x x0
z z0
=
=
a2
a1
a3
……………………

37. Примеры решения задач

Задача 4. Найти угол между прямой d и плоскостью π в системе координат
R 0, i , j , k , если известны уравнения этой прямой и плоскости:
d:
x x1
z z1
y y1
=
=
;
a1
a3
a2
π: Ax+ By+Cz+D = 0 , где А2+В2+С2 ≠ 0.

38. Алгоритм применения метода координат к решению геометрических задач сводится к следующему:

Выбираем в пространстве систему координат из
соображений удобства выражения координат и
наглядности изображения.
Находим координаты необходимых для нас точек.
Решаем задачу, используя основные задачи
метода координат.
Переходим от аналитических соотношений к
геометрическим

39. Примеры решения задач

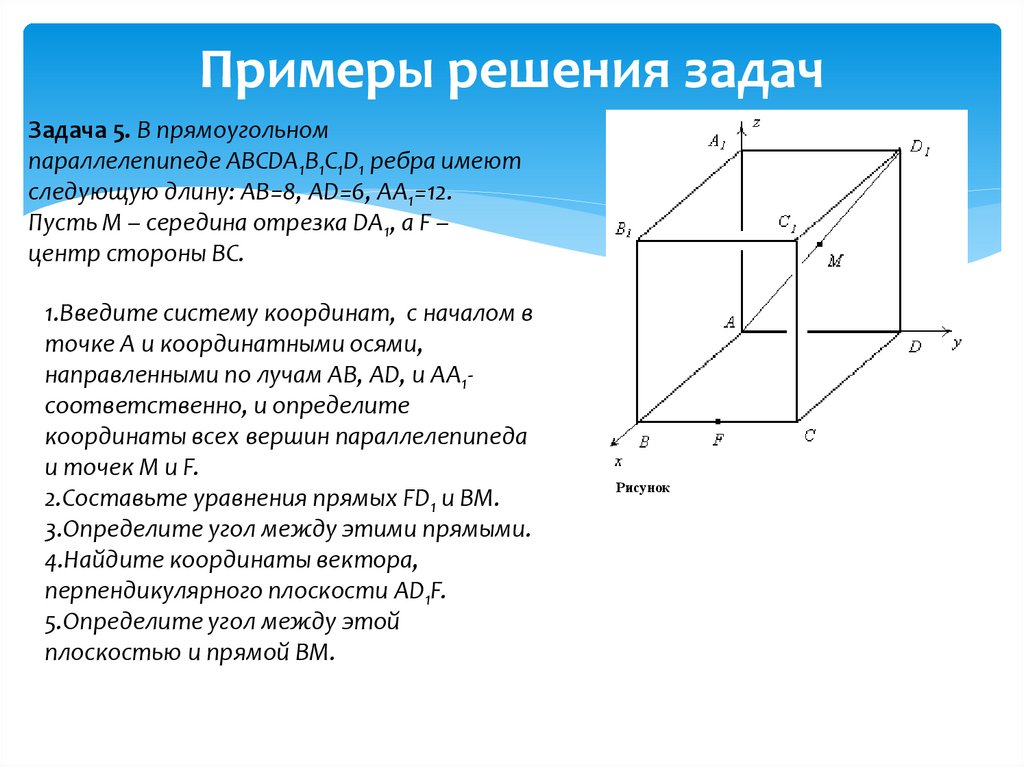
Задача 5. В прямоугольном
параллелепипеде ABCDA1B1C1D1 ребра имеют
следующую длину: AB=8, AD=6, AA1=12.
Пусть М – середина отрезка DA1, а F –
центр стороны BC.
1.Введите систему координат, с началом в
точке А и координатными осями,
направленными по лучам AB, AD, и AA1соответственно, и определите
координаты всех вершин параллелепипеда
и точек M и F.
2.Составьте уравнения прямых FD1 и BM.
3.Определите угол между этими прямыми.
4.Найдите координаты вектора,
перпендикулярного плоскости AD1F.
5.Определите угол между этой
плоскостью и прямой BM.
Рисунок

40. Примеры решения задач

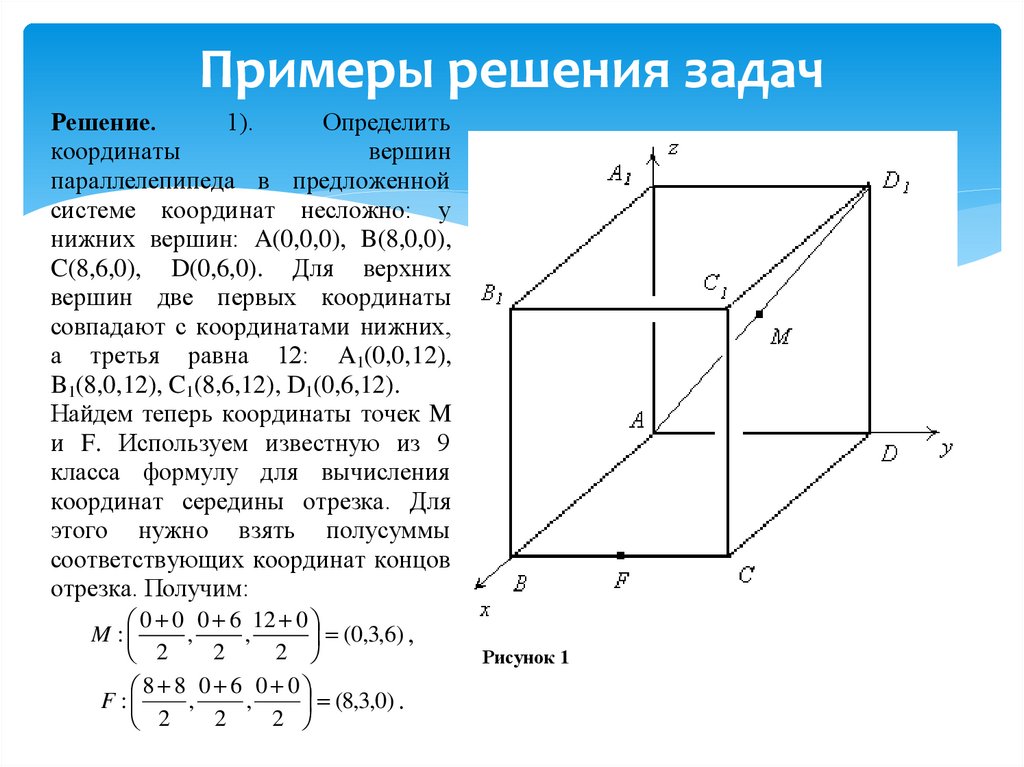
Решение.
1).
Определить
координаты
вершин
параллелепипеда в предложенной
системе координат несложно: у
нижних вершин: A(0,0,0), B(8,0,0),
C(8,6,0), D(0,6,0). Для верхних
вершин две первых координаты
совпадают с координатами нижних,
а третья равна 12: A1(0,0,12),
B1(8,0,12), C1(8,6,12), D1(0,6,12).
Найдем теперь координаты точек M
и F. Используем известную из 9
класса формулу для вычисления
координат середины отрезка. Для
этого нужно взять полусуммы
соответствующих координат концов
отрезка. Получим:
0 0 0 6 12 0
M :
,
,
(0,3,6) ,
2
2
2
8 8 0 6 0 0
F :
,
,
(8,3,0) .
2
2
2
Рисунок 1

41. Примеры решения задач

2)
Составим уравнения прямых, используя формулы (11):
x 0 y 6 z 12
x 0 y 6 z 12
,
8 0 3 6 0 12
8
3
12
x 0 y 3 z 6
x 0 y 3 z 6
BM:
.
8 0 0 3 0 6
8
3
6
FD1:
3)
Угол между прямыми определим как угол между их направляющими
векторами с помощью формулы
(12). Учитывая, что направляющие векторы имеют
координаты: a 8, 3, 12 , b 8, 3, 6 .
cosφ= cos =
a1b1 a2b2 a3b3
a a a b b b
2
1
2
2
2
3
2
1
2
2
2
3
cosφ
8 8 ( 3)( 3) ( 12)( 6)
8 ( 3) ( 12) 8 ( 3) ( 6)
2
2
145
.
217 109
2
2
2
2
,

42. Примеры решения задач

4) Найдем координаты вектора, перпендикулярного плоскости AD1F. Для этого
используем признак перпендикулярности векторов: два вектора перпендикулярны,
если их скалярное произведение равно нулю. Пусть интересующий нас вектор n
имеет координаты {x,y,z}. Векторы AD1 и AF лежат в интересующей нас
плоскости, и имеют координаты {0,6,12} и {8,3,0} соответственно. Используем
формулу (3) для вычисления скалярных произведений в координатах, приравняем
эти произведения к нулю и получим систему уравнений:
0 x 6 y 12 z 0
3
, выразим в этой системе x и z через y: x y,
8
8x 3 y 0 z 0
1
z y . Как мы
2
видим, получилось множество векторов, перпендикулярных данной плоскости,
координаты которых зависят от параметра y. Выберем один из них, положив, для
удобства, что y=-8. Итак n ={3,-8,4}.
5) Нам осталось определить угол между прямой BM и плоскостью AD1F. Для этого
мы используем формулу (16): sin
Aa1 Ba 2 Ca3
. Здесь A,B и С – по
A B C a a a
сути, координаты вектора
n ={3,-8,4}, а {a1,a2,a3} – координаты направляющего
вектора прямой BM: b 8, 3, 6 . Подставив все эти значения в формулу, получим:
Aa1 Ba 2 Ca3
3 8 ( 8)( 3) 4( 6)
sin
A2 B 2 C 2 a12 a22 a32
32 ( 8) 2 4 2 82 ( 3) 2 ( 6) 2
sin
12
.
89 109
2
2
2
2
1
2
2
2
3

43. Примеры решения задач

44.

Многие задачи в математике решаются методом
координат, суть которого состоит в следующем:
Задавая фигуры уравнениями (неравенствами) и
выражая в координатах различные
геометрические соотношения, мы применяем
алгебру к решению геометрических задач;
Пользуясь координатами, можно истолковывать
алгебраические соотношения геометрически,
применяя геометрию к решению алгебраических
задач.

45.

СПАСИБО
ЗА
ВНИМАНИЕ!