Похожие презентации:
Основы гидрогазодинамики. Теплоэнергетика и теплотехника
1.
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ»
2.
ИНСТИТУТ НЕФТИ, ГАЗА И ЭНЕРГЕТИКИЛЕКЦИЯ
по дисциплине
«Гидрогазодинамика»
Тема лекции «Основы гидрогазодинамики»
Кочарян Евгений Валерьевич
доцент кафедры
Теплоэнергетика и теплотехника
3.
Список используемой литературы1. Рабинович Е.З. Гидравлика.- М.: «Недра», 1980.- 278 с.
2. Гидрогазодинамика / М.Е. Дейч, А.Е. Зарякин. - М.:
Энергоатомиздат, 1984.
3. Повх И.Л. Техническая гидромеханика. 2-е изд., доп., Л.,
«Машиностроение», 1976. – 504 с.
4. Кочарян Е.В., Арестенко Ю.П. Техническая гидрогазодинамика:
учеб. пособие / Кубан. гос. технол. ун-т. – Краснодар: Изд. ФГБОУ ВО
«КубГТУ», 2016. – 123 с.
5. Арустамова И.Т., Иванников В.Г. Гидравлика: Учебное пособие
для ВУЗов (Рекомендовано ГК РФ по высшему образованию) – М.:
Недра. 1995 -198 стр.
4.
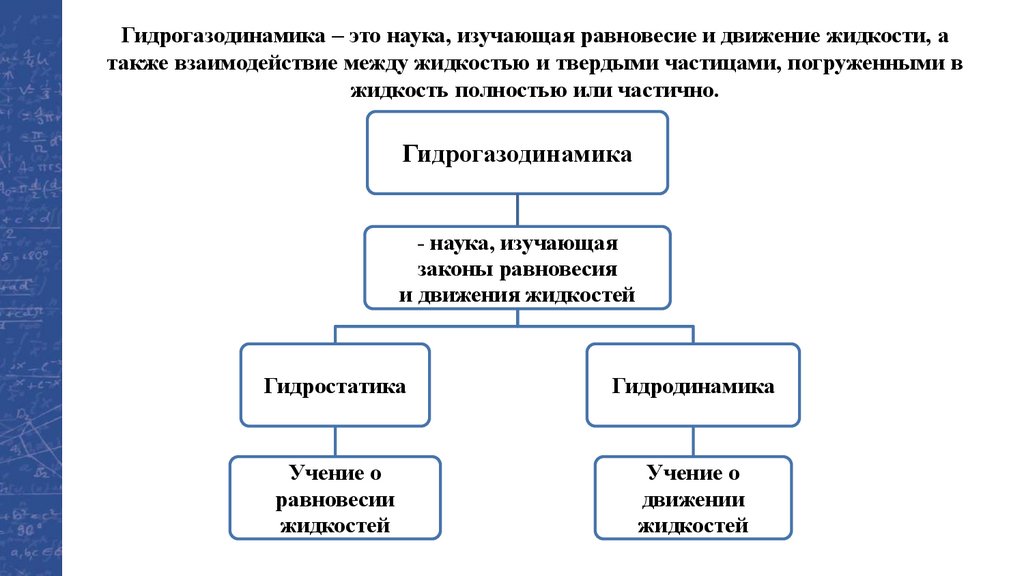
Гидрогазодинамика – это наука, изучающая равновесие и движение жидкости, атакже взаимодействие между жидкостью и твердыми частицами, погруженными в
жидкость полностью или частично.
Гидрогазодинамика
- наука, изучающая
законы равновесия
и движения жидкостей
Гидростатика
Гидродинамика
Учение о
равновесии
жидкостей
Учение о
движении
жидкостей
5.
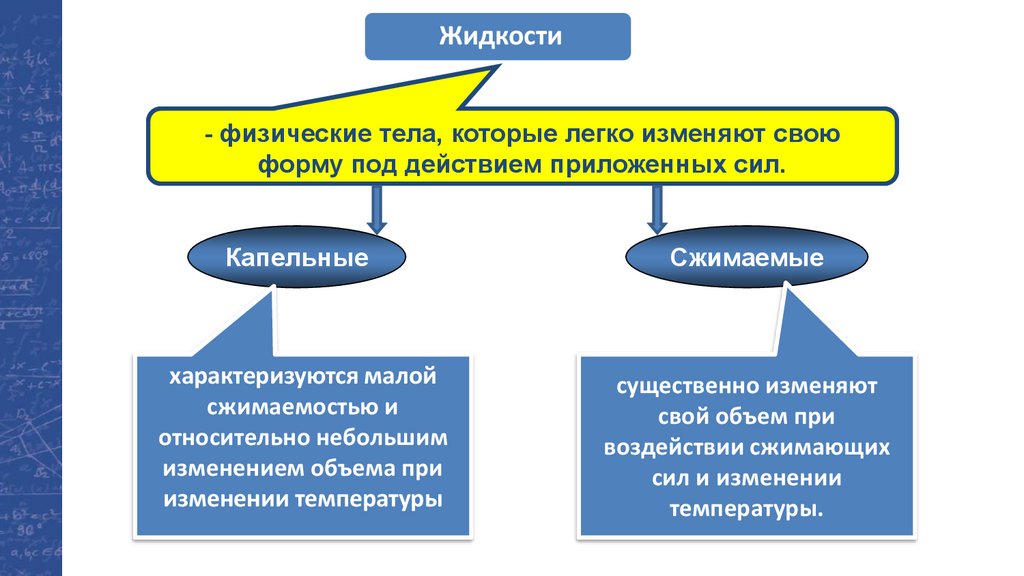
Жидкости- физические тела, которые легко изменяют свою
форму под действием приложенных сил.
Капельные
Сжимаемые
характеризуются малой
сжимаемостью и
относительно небольшим
изменением объема при
изменении температуры
существенно изменяют
свой объем при
воздействии сжимающих
сил и изменении
температуры.
6.
Для решения задач гидравлики используют понятие об идеальной жидкости, т.е.жидкости абсолютно несжимаемой и не обладающей вязкостью.
Основные физические свойства жидкостей
Плотность и удельный вес. К основным физическим свойствам жидкостей следует отнести те её
свойства, которые определяют особенности поведения жидкости при её движении.
Важнейшим физическим свойством жидкости, определяющим её концентрацию в
пространстве, является плотность жидкости. Под плотностью жидкости понимается масса
единицы объёма жидкости
где m– масса жидкости;
V – объём, занимаемый жидкостью.
Плотность среды зависит от температуры и давления.
Удельный вес
- вес единицы объема
жидкости.
кг/м³
(СИ)
Н/м³
(СИ).
7.
Величины плотности реальных капельных жидкостей в стандартных условиях изменяются в системе единиц СИ в широких пределах от 700 кг/м3 до 1800 кг/м3, аплотность ртути достигает 13550 кг/м3 , плотность чистой воды составляет 998 кг/м 3.
Величины плотности газов меньше плотности капельных жидкостей приблизительно
на три порядка, т. е. в системе единиц СИ плотности газов при атмосферном давлении и
температуре 0 °С изменяются в пределах от 0,09 кг/м3 до 3,74 кг/м3 , плотность воздуха
составляет 1,293 кг/м 3.
Плотность капельных жидкостей и газов зависит от температуры и давления.
Зависимость величины плотности жидкости и газа при температуре отличной от 20 °С
определяется по формуле Д.И. Менделеева
где
°С;
ρi и ρ20 – плотности жидкости (газа) при температурах соответственно Т и То=20
βi – коэффициент температурного расширения.
Удивительно, но факт! ВОДА обладает исключительными особенностями,
максимальная плотность которой отмечается при 4 °С - 1000 кг/м3!
8.
Сжимаемость. Способность жидкости или газа под действием внешнего давленияизменять свой объем и, следовательно, плотность называется сжимаемостью.
Коэффициент объёмного сжатия жидкости представляет собой относительное
изменение объёма жидкости при изменении давления на единицу. По существу это
известный закон Гука для модели объёмного сжатия
где
W0 – начальный объём жидкости (при начальном давлении);
βV - коэффициент объёмного (упругого) сжатия жидкости [1/Па].
Модуль упругости
– величина, обратная коэффициенту сжимаемости.
Температурное
расширение
капельных
жидкостей
коэффициентом температурного расширения βt , °C-1
характеризуется
где dW – изменение этого объема при повышении температуры на величину dt.
9.
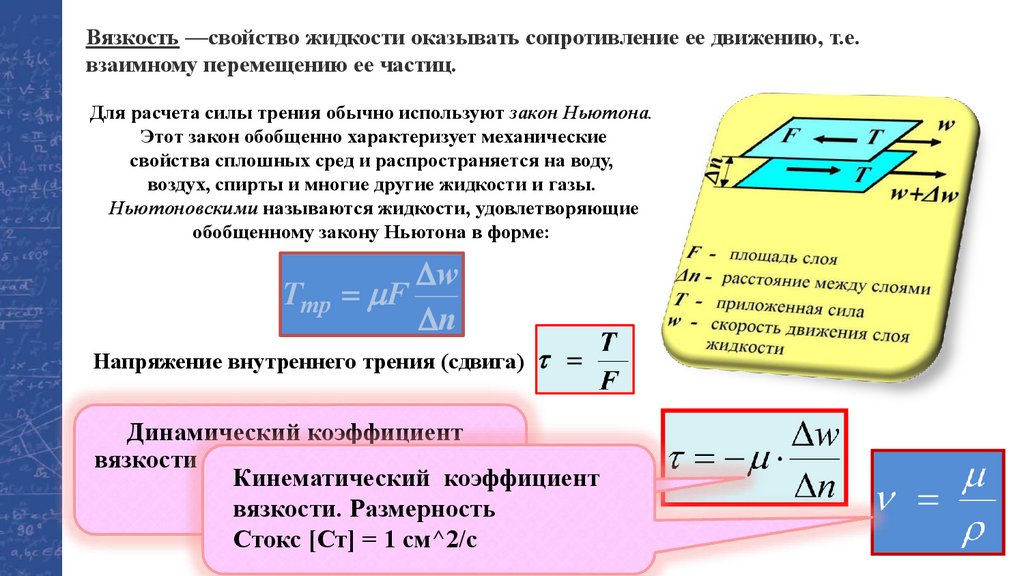
Вязкость —свойство жидкости оказывать сопротивление ее движению, т.е.взаимному перемещению ее частиц.
Для расчета силы трения обычно используют закон Ньютона.
Этот закон обобщенно характеризует механические
свойства сплошных сред и распространяется на воду,
воздух, спирты и многие другие жидкости и газы.
Ньютоновскими называются жидкости, удовлетворяющие
обобщенному закону Ньютона в форме:
w
Tтр = F
n
Напряжение внутреннего трения (сдвига)
Динамический коэффициент
вязкости (вязкость). Размерность –
Кинематический
коэффициент
Па ∙ с
вязкости. Размерность
Стокс [Ст] = 1 см^2/с
10.
ГИДРОСТАТИКАСилы, действующие в жидкости
По характеру действия силы можно разделить на две категории: массовые силы
и поверхностные.
Массовые силы пропорциональны массе тела и действуют на каждую жидкую частицу. К
категории массовых сил относятся силы тяжести и силы инерции движения.
Поверхностные силы равномерно распределены по поверхности и пропорциональны
площади этой поверхности. В общем случае поверхностные силы имеют две составляющие –
нормальную и тангенциальную. Единичная поверхностная сила называется напряжением.
Нормальная составляющая поверхностных сил называется силой давления F, а напряжение
(единичная сила) называется давлением
где S – площадь поверхности.
Величина давления (иногда в литературе называется гидростатическим
давлением) в системе СИ измеряется в паскалях: 1 Па= Н / м2.
Поскольку эта величина очень мала, то величину давления принято измерять в
мегапаскалях (МПа) и килопаскалях (кПа): 1 МПа = 1 × 10 6 Па; 1 кПа = 1 × 10 3 Па.
Употребляются до сих пор также следующие единицы измерения давления:
1 am = 1 кгс/см2 = 0,1 МПа=1 бар; 1 МПа = 10 Аm; 1 Ат=101325 Па = 760 мм. рт.
ст; 1 кгс/м2=10 –4 кгс/см2=1 мм вод. cт.
11.
Различают давление абсолютное, избыточное и давление вакуума.Абсолютным давлением называется давление в точке измерения,
отсчитанное от нуля. Если за уровень отсчёта принята величина
атмосферного давления, то разница между абсолютным и атмосферным
называется избыточным давлением
Если давление, измеряемое в точке, ниже
величины атмосферного давления, то разница
между замеренным давлением и атмосферным
называется давлением вакуума
Избыточное давление в жидкостях измеряется
манометрами. Это весьма обширный набор
измерительных приборов различной конструкции
и различного исполнения.
12.
Торичелли:не насос втягивает воду, а атмосферное
давление её поднимает вверх, когда на
всасывающей линии насоса образуется
разреженное пространство (рвх < ратм )
Свойства гидростатического давления
Действующее на внешнюю поверхность жидкости давление обладает следующими
основными свойствами:
1. Давление всегда направлено по внутренней нормали к выделенной поверхности.
2. В любой точке внутри жидкости давление по всем направлениям одинаково. Другими словами величина давления в точке не зависит от ориентации площадки, на
которую действует давление.
3. Для жидкости, находящейся в состоянии равновесия, справедлив так называемый
закон Паскаля, утверждающий, что всякое изменение давления в какой-либо точке
жидкости передаётся мгновенно и без изменения во все остальные точки жидкости.
13.
Основное уравнение гидростатикиОчевидно,
равнодействующая
всех
сил,
направленных вертикально, будет равна нулю, так
как тело находится в равновесии.
P − P1 − G = 0
p x y − p1 x y − g z x y = 0
p = p1 + g z
p = p0 + gН
.
основное уравнение
гидростатики
Гидростатическое давление в жидкости
пропорционально высоте ее слоя и на одинаковой
глубине имеет одну и ту же величину во всех точках
жидкости.
14.
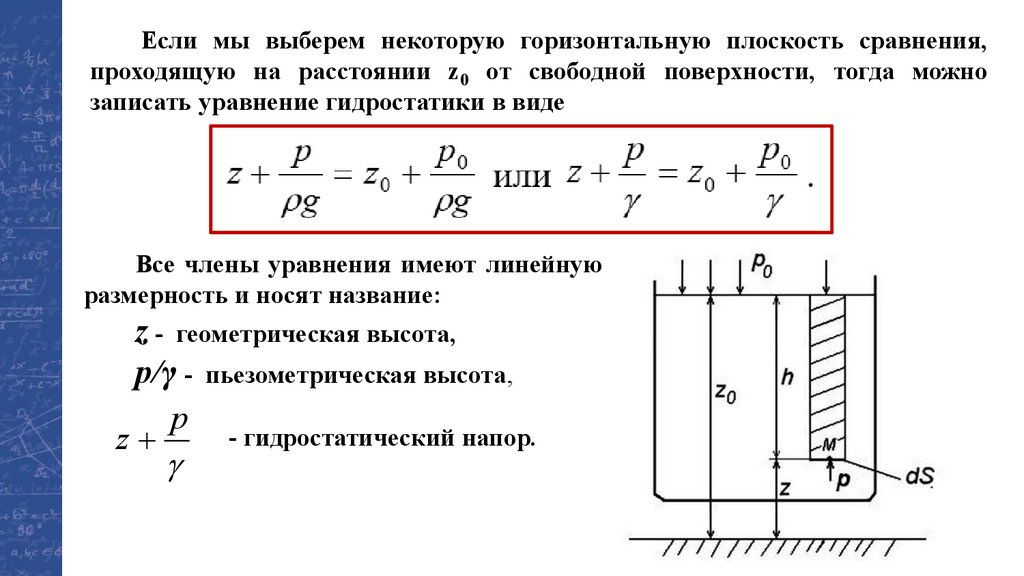
Если мы выберем некоторую горизонтальную плоскость сравнения,проходящую на расстоянии z0 от свободной поверхности, тогда можно
записать уравнение гидростатики в виде
Все члены уравнения имеют линейную
размерность и носят название:
z - геометрическая высота,
p/γ - пьезометрическая высота,
p
- гидростатический напор.
z+
15.
Сообщающиеся сосудыВ своей практической деятельности человек часто сталкивается с вопросами равновесия
жидкости в сообщающихся сосудах, когда два сосуда А и В соединены между собой жёстким или
гибким шлангом. Сами сосуды (А и В) обычно называются коленами. Такой гидравлический
элемент часто используется в различных гидравлических машинах (гидравлические прессы и
др.), системах гидропривода и гидроавтоматики, различных измерительных приборах и в ряде
других случаев.
В открытых сообщающихся сосудах, заполненных однородной жидкостью, свободный
уровень жидкости устанавливается на одном и том же уровне в обоих коленах. Если в коленах
сосудов залиты две несмешивающиеся жидкости с различной плотностью, то свободные уровни
жидкости в правом и левом коленах устанавливаются на разных высотах в зависимости от
соотношения плотностей жидкостей.
16.
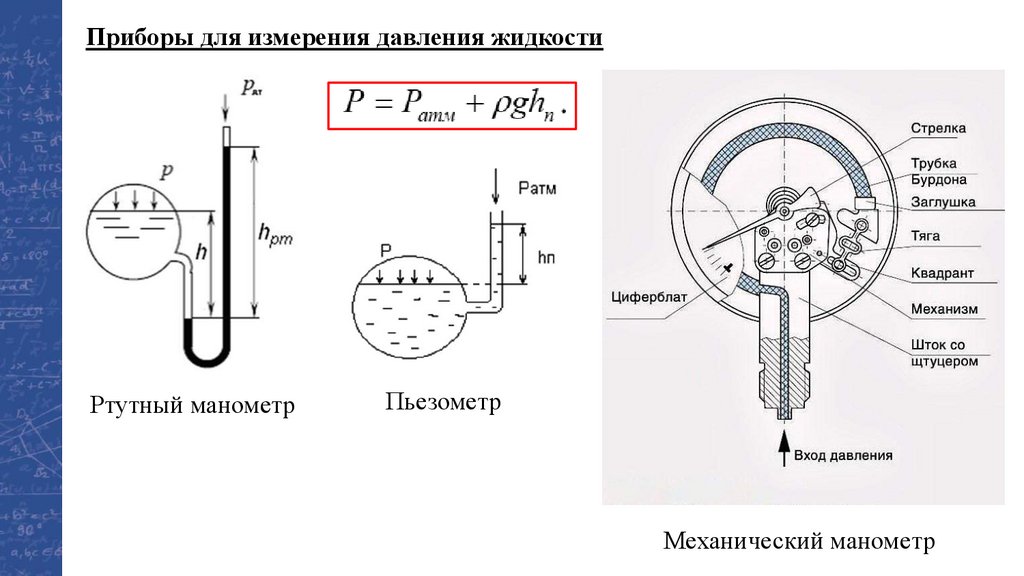
Приборы для измерения давления жидкостиРтутный манометр
Пьезометр
Механический манометр
17.
ГИДРОДИНАМИКАРасход - количество жидкости, протекающее через живое сечение потока в
единицу времени.
Различают массовый расход G [кг/с] и объемный расход Q [куб.м/с].
Массовый m и объемный Q расходы связаны соотношением
G = Qρ
Скорость движения потока характеризуется средней скоростью в
данном поперечном сечении, м/с:
w=Q/F=Q/S
где F (или S) – площадь поперечного сечения потока, м2.
18.
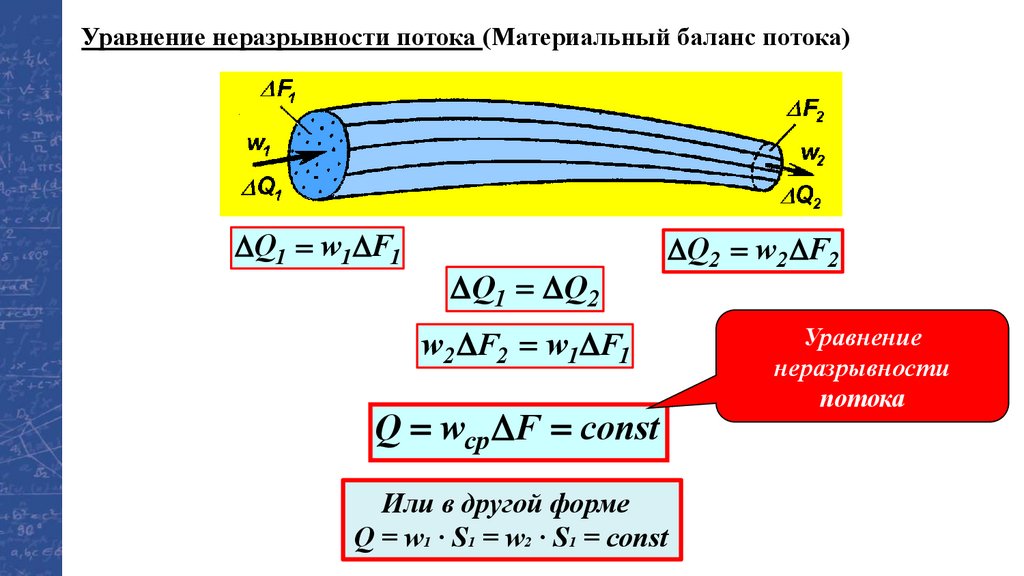
Уравнение неразрывности потока (Материальный баланс потока)Q1 = w1 F1
Q1 = Q2
Q2 = w2 F2
w2 F2 = w1 F1
Q = wcp F = const
Или в другой форме
Q = w1 · S1 = w2 · S1 = const
Уравнение
неразрывности
потока
19.
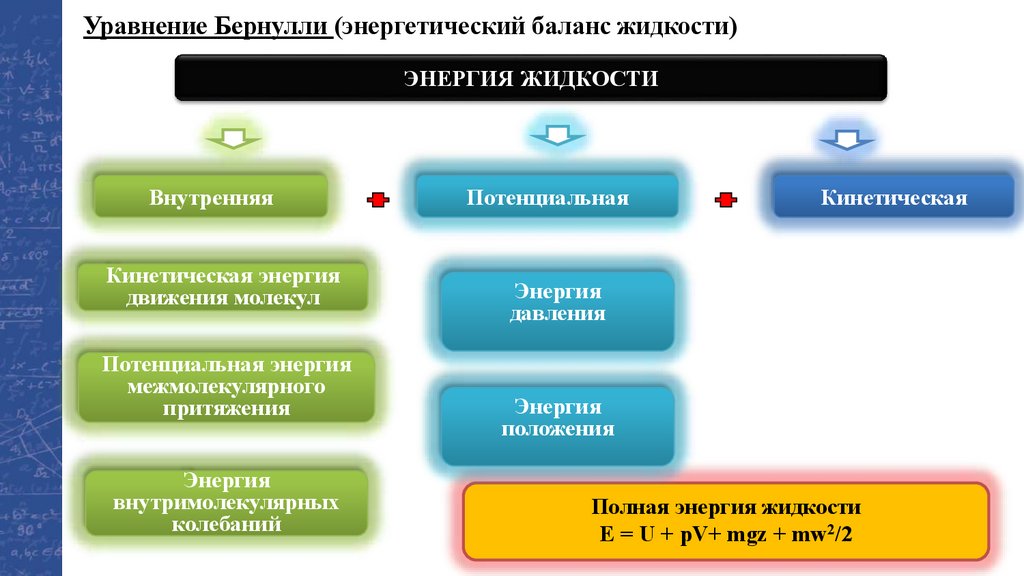
Уравнение Бернулли (энергетический баланс жидкости)ЭНЕРГИЯ ЖИДКОСТИ
Внутренняя
Кинетическая энергия
движения молекул
Потенциальная энергия
межмолекулярного
притяжения
Энергия
внутримолекулярных
колебаний
Потенциальная
Кинетическая
Энергия
давления
Энергия
положения
Полная энергия жидкости
E = U + pV+ mgz + mw2/2
20.
Уравнение Бернулли для идеальной жидкостиw12
p2
w22
u1 +
+ gz1 +
= u2 +
+ gz2 +
2
2
p1
p1 w12
p2 w22
z1 +
+
= z2 +
+
g 2 g
g 2 g
u1=u2
уравнение Бернулли
для идеальной жидкости
Уравнение Бернулли является частным случаем закона сохранения энергии
и выражает энергетический баланс потока: полная удельная энергия
жидкости есть величина постоянная во всех сечениях потока.
21.
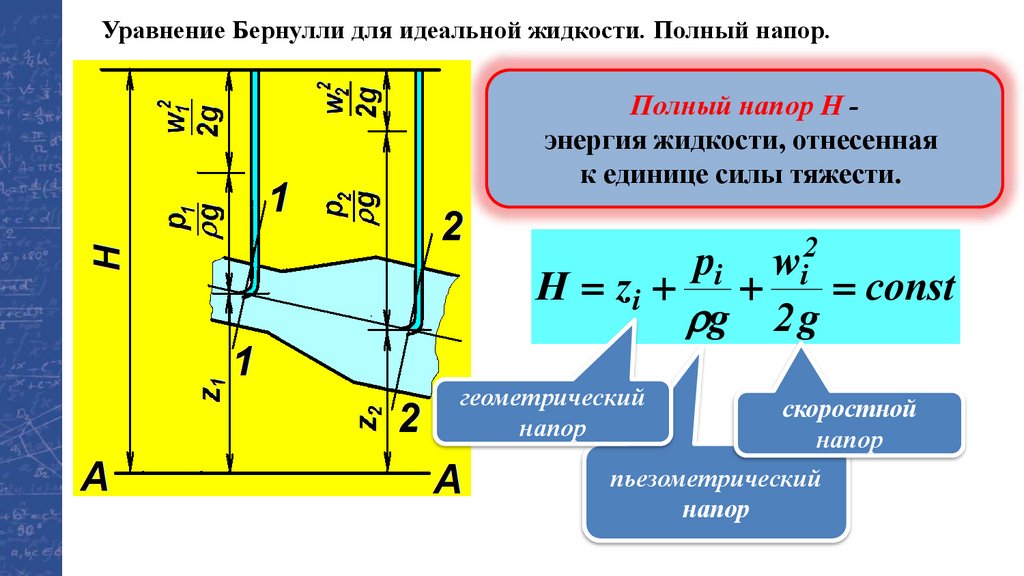
Уравнение Бернулли для идеальной жидкости. Полный напор.Полный напор Н энергия жидкости, отнесенная
к единице силы тяжести.
pi wi2
H = zi +
+
= const
g 2 g
геометрический
напор
скоростной
напор
пьезометрический
напор
22.
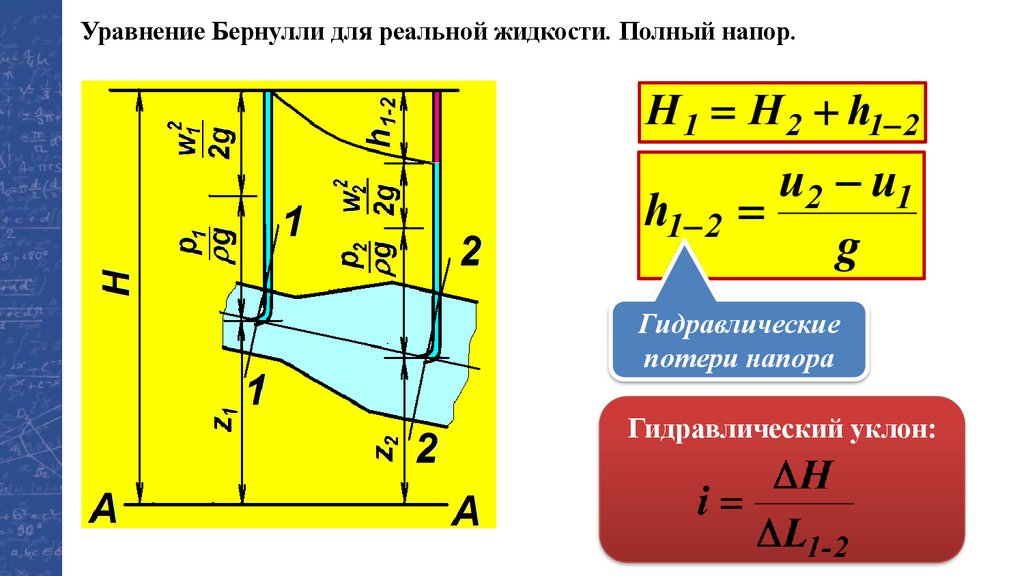
Уравнение Бернулли для реальной жидкостиw12
p2
w22
u1 +
+ gz1 +
= u2 +
+ gz2 +
2
2
p1
p1 w12
p2 w22
z1 +
+
= z2 +
+
+ h1− 2
g 2 g
g 2 g
уравнение Бернулли
для реальной жидкости
В отличие от идеальной жидкости, для которой
полный напор Н = const, для реальной жидкости полный напор
убывает по направлению движения жидкости
Из уравнения Бернулли следует, что
увеличение скоростного напора
сопровождается соответствующим уменьшением
пьезометрического напора и наоборот.
23.
Уравнение Бернулли для реальной жидкости. Полный напор.H 1 = H 2 + h1− 2
u2 − u1
h1− 2 =
g
Гидравлические
потери напора
Гидравлический уклон:
24.
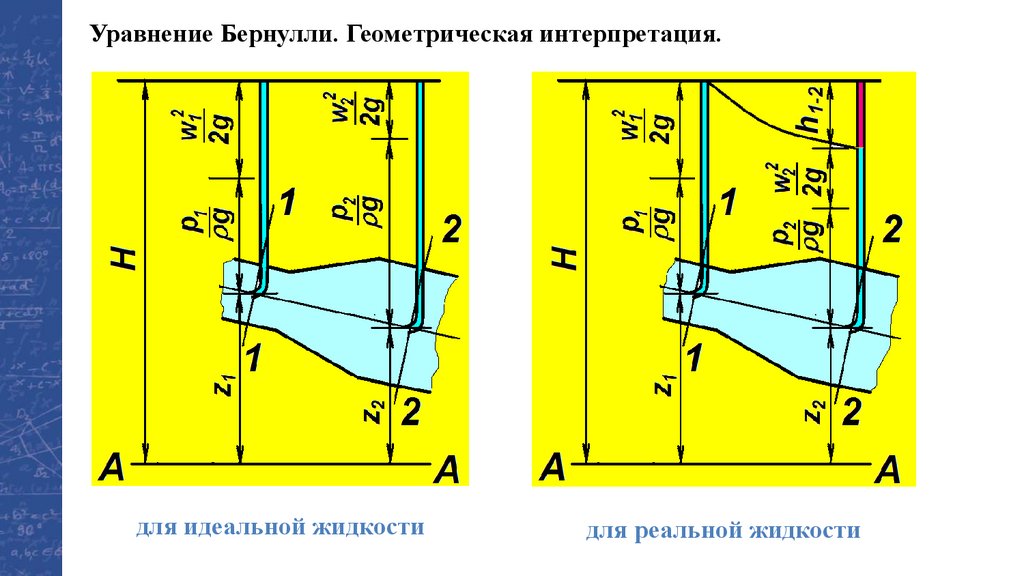
Уравнение Бернулли. Геометрическая интерпретация.для идеальной жидкости
для реальной жидкости
25.
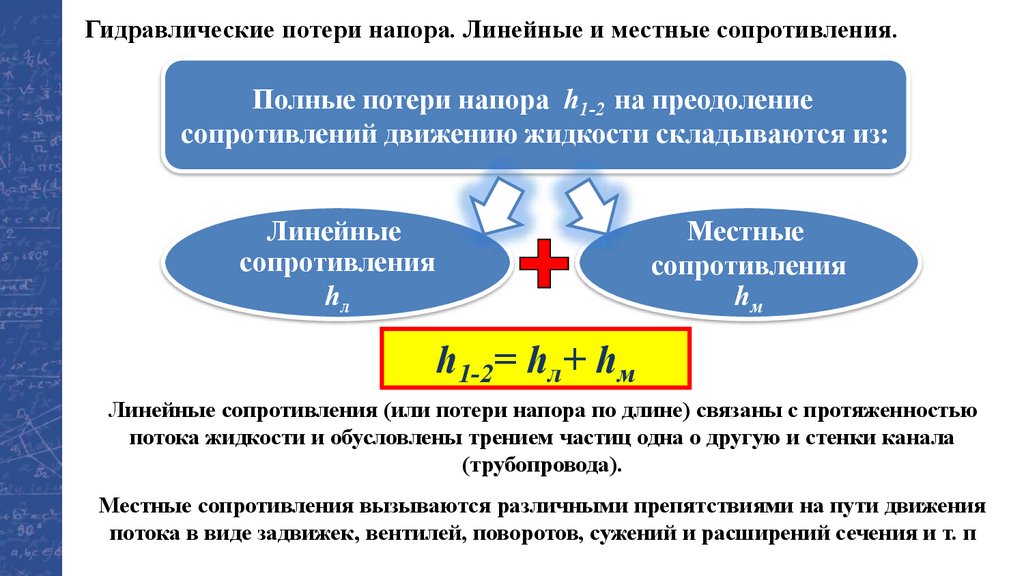
Гидравлические потери напора. Линейные и местные сопротивления.Полные потери напора h1-2 на преодоление
сопротивлений движению жидкости складываются из:
Линейные
сопротивления
hл
Местные
сопротивления
hм
h1-2= hл+ hм
Линейные сопротивления (или потери напора по длине) связаны с протяженностью
потока жидкости и обусловлены трением частиц одна о другую и стенки канала
(трубопровода).
Местные сопротивления вызываются различными препятствиями на пути движения
потока в виде задвижек, вентилей, поворотов, сужений и расширений сечения и т. п
26.
Сопротивление при движении жидкости по трубопроводу.Местные сопротивления.
Местное сопротивление – это короткий участок трубопровода,
на котором скорость потока претерпевает изменения или по величине ,
или по направлению .
К местным сопротивлениям относятся вход в трубу и выход из нее,
участки сжатия и расширения потока, различные фитинги, диафрагмы,
запорные и регулирующие устройства.
Потери напора в местном
сопротивлении:
где ξм —
коэффициент
местного
сопротивления.
Величина ξм зависит как от вида местного сопротивления, так и от
режима движения жидкости. Для различных местных
сопротивлений величины ξм приводятся в справочниках.
27.
Sм = 1− 1
S2
м = 0 ,14
м = 1,1 1,3
28.
Сопротивление при движении жидкости по трубопроводу.Потери на трение по длине.
Потери напора на
трение:
w2
h1− 2 =
d гидр 2 g
l
Коэффициент гидравлического
сопротивления
Для круглого трубопровода dгидр = d
Гидравлический (эквивалентный) радиус - отношение
площади живого сечения потока F к смоченному
периметру П. позволяют использовать уравнения
гидравлики для трубопроводов (каналов), имеющих
некруглую форму поперечного сечения
Потеря напора на трение пропорциональна длине трубопровода l и скоростному
напору w2/2g и обратно пропорциональна диаметру трубы d.
29.
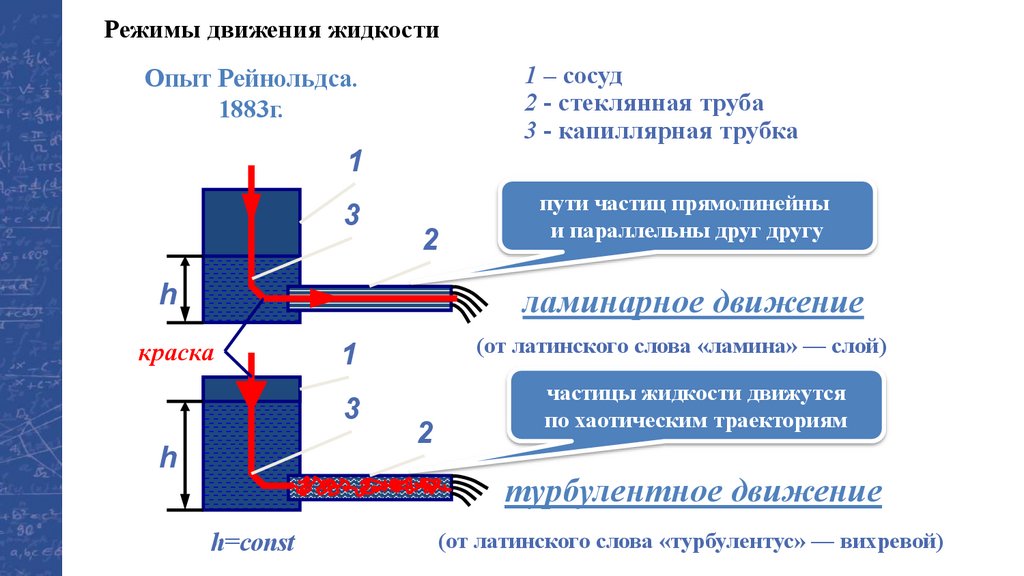
Режимы движения жидкости1 – сосуд
2 - стеклянная труба
3 - капиллярная трубка
Опыт Рейнольдса.
1883г.
1
3
2
пути частиц прямолинейны
и параллельны друг другу
ламинарное движение
h
краска
3
h
(от латинского слова «ламина» — слой)
1
2
частицы жидкости движутся
по хаотическим траекториям
турбулентное движение
h=const
(от латинского слова «турбулентус» — вихревой)
30.
Режимы движения жидкостиОпыт показывает, что переход от ламинарного течения к турбулентному
зависит от массовой скорости жидкости ρw, диаметра трубы d и вязкости
жидкости μ.
Критерий Рейнольдса:
Re =
wd
=
wd
Re < 2300 – устойчивый ламинарный режим
2300 < Re < 10000 – неустойчиво турбулентный
режим
Re > 10000 – устойчиво турбулентный режим
Reкр=2300
31.
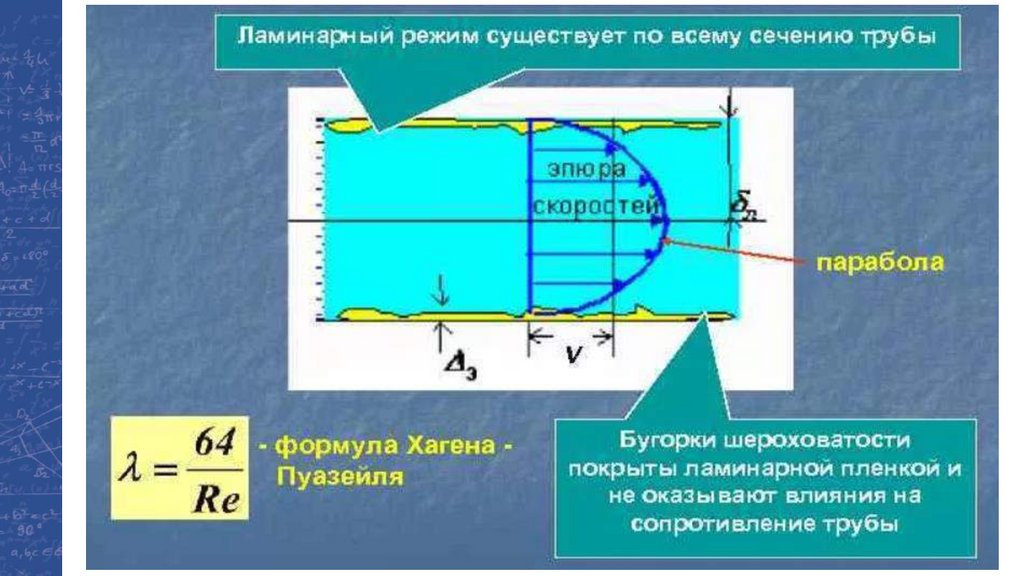
Распределение скоростей по сечению потока при ламинарном режимер1 и р2 – гидростатические
давления в сечениях трубы на
расстоянии l;
wy – скорость движения
жидкости
на расстоянии y от оси трубы
32.
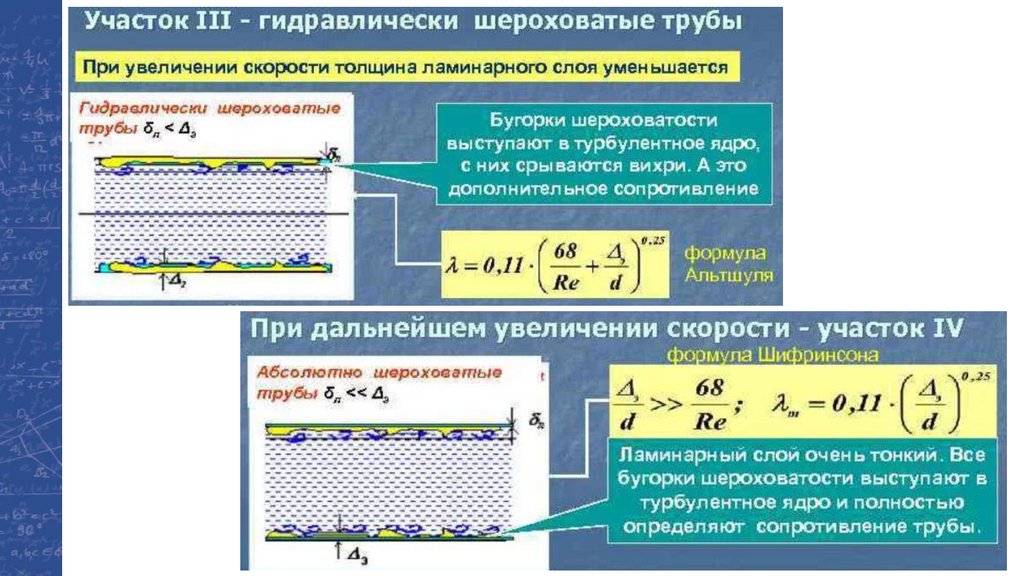
Распределение скоростей по сечению потока при турбулентном режимепульсация
скоростей,
перемешивание
жидкости
в ядре потока
скорости частиц
одинаковы
ламинарный
пограничный слой
переходная зона
= 62 ,8 dRe
-0,875
33.
Распределение скоростей по сечению потока при ламинарном итурбулентном режимах
Характерное распределение скоростей для каждого режима движения
жидкости устанавливается (стабилизируется) на протяжении некоторого
участка трубопровода, называемого начальным.
34.
35.
36.
Движение жидкостей в трубопроводах37.
38.
39.
40.
41.
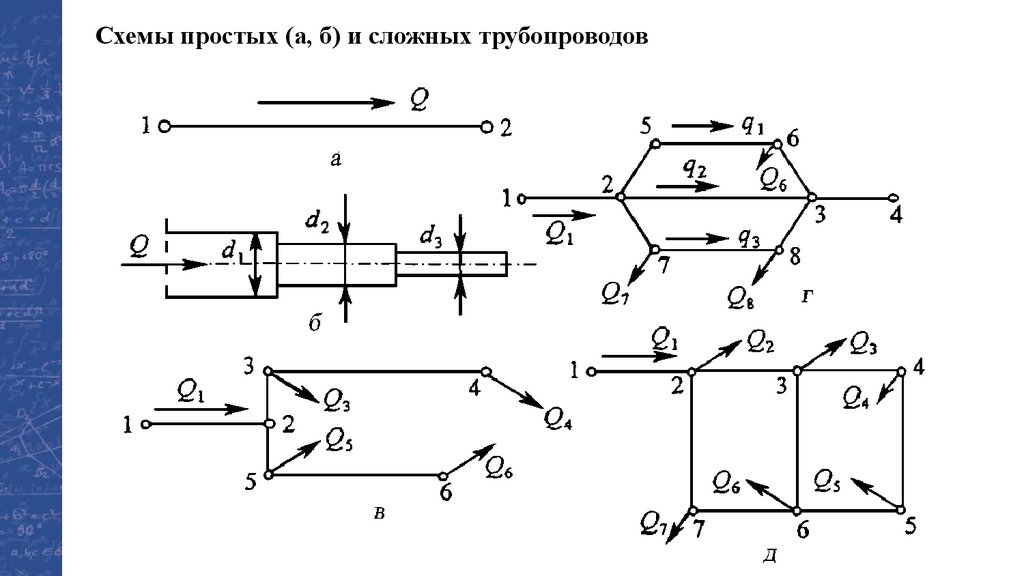
Схемы простых (а, б) и сложных трубопроводов42.
Расчет простых трубопроводов43.
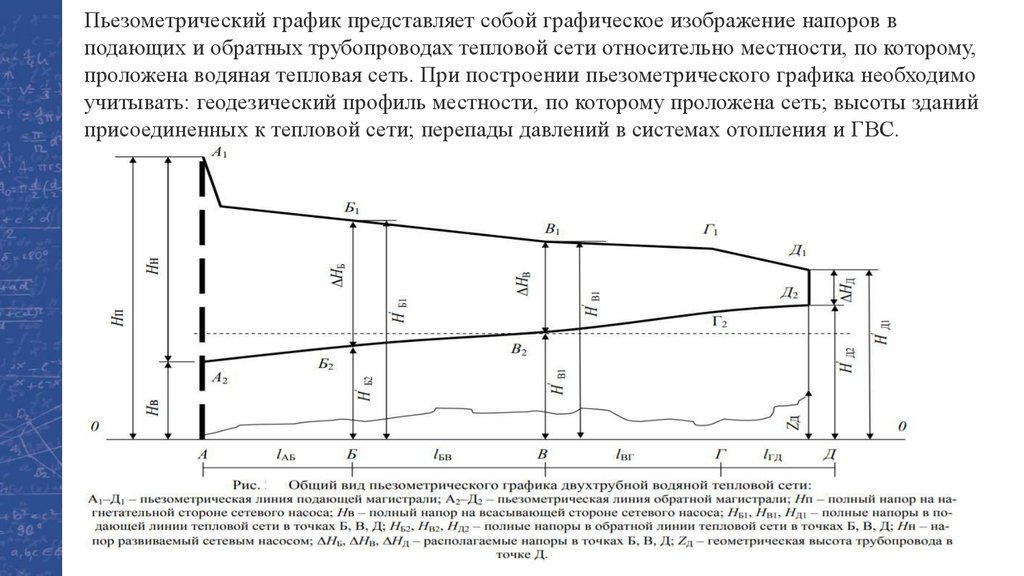
Пьезометрический график представляет собой графическое изображение напоров вподающих и обратных трубопроводах тепловой сети относительно местности, по которому,
проложена водяная тепловая сеть. При построении пьезометрического графика необходимо
учитывать: геодезический профиль местности, по которому проложена сеть; высоты зданий
присоединенных к тепловой сети; перепады давлений в системах отопления и ГВС.
44.
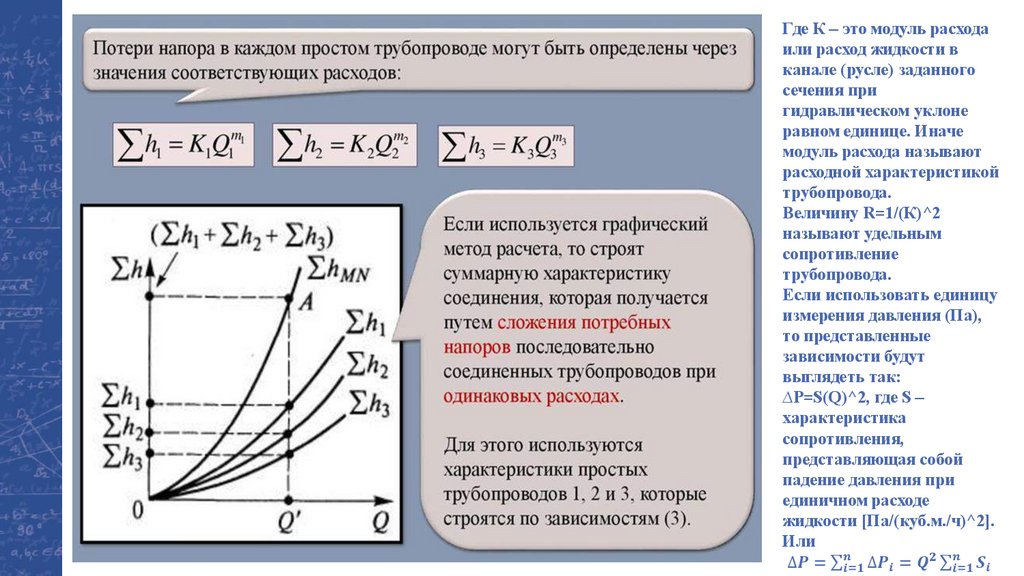
Где К – это модуль расходаили расход жидкости в
канале (русле) заданного
сечения при
гидравлическом уклоне
равном единице. Иначе
модуль расхода называют
расходной характеристикой
трубопровода.
Величину R=1/(К)^2
называют удельным
сопротивление
трубопровода.
Если использовать единицу
измерения давления (Па),
то представленные
зависимости будут
выглядеть так:
∆Р=S(Q)^2, где S –
характеристика
сопротивления,
представляющая собой
падение давления при
единичном расходе
жидкости [Па/(куб.м./ч)^2].
Или
∆































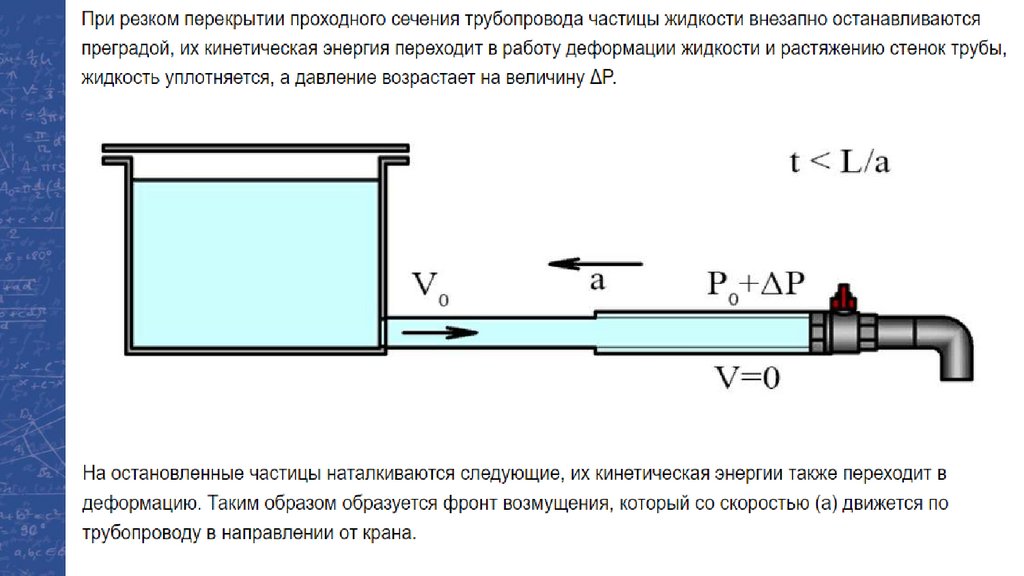
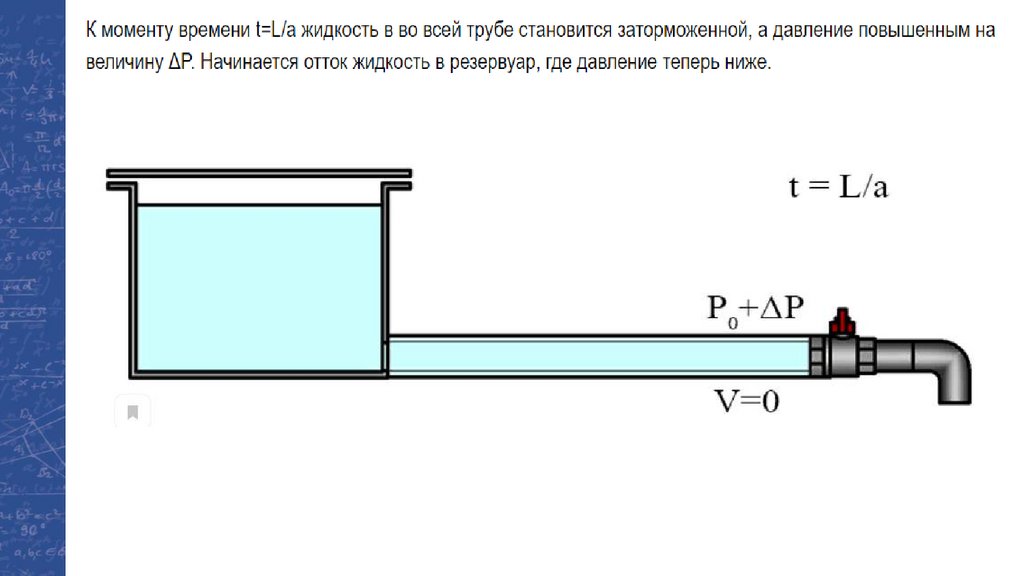

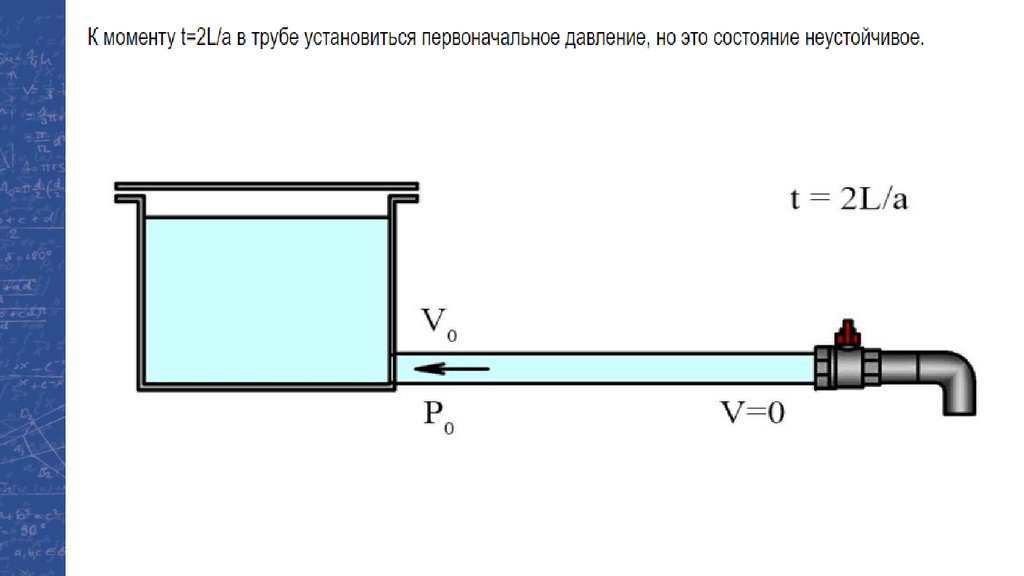


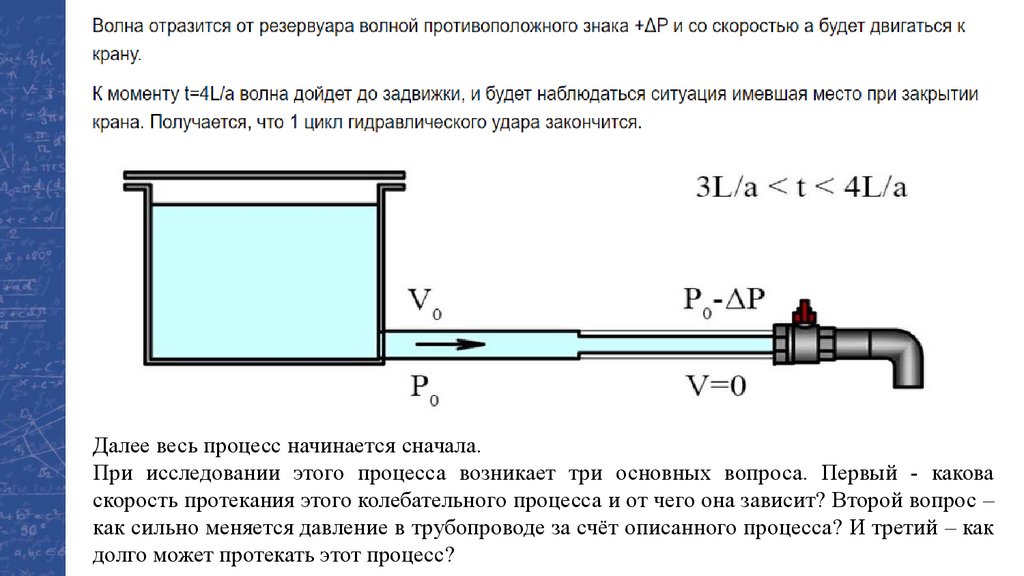


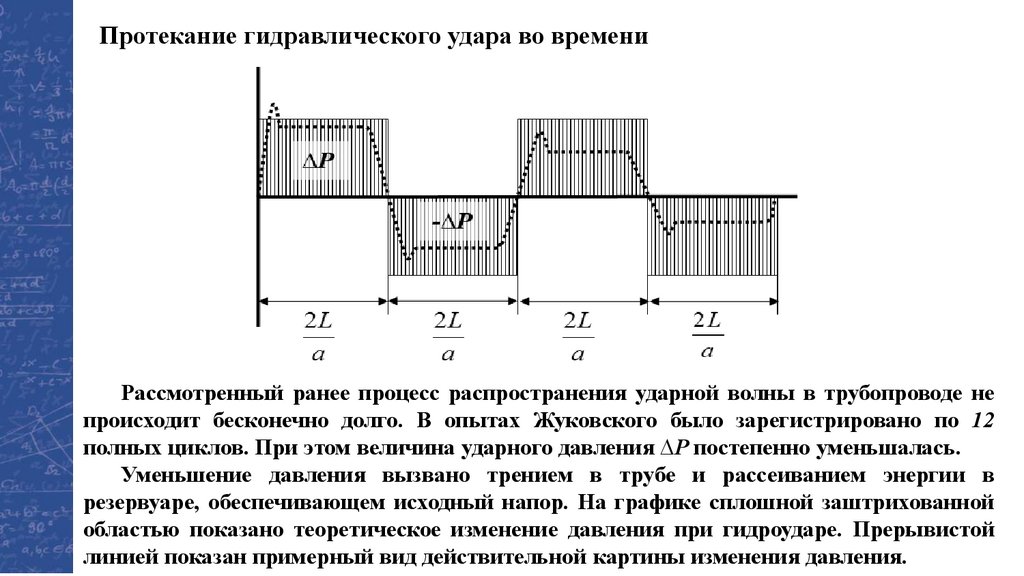








 Физика
Физика








