Похожие презентации:
Логарифмическая функция
1.
Повторение и обобщение знанийУчитель математики Е.Б.Степанова ГОУ СОШ №571
Невского района г. Санкт-Петербурга
2.
Функцияу log а х ( а > 0, а ≠ 1), обратная к
показательной функции у а х , называется
логарифмической функцией по основанию а .
Свойства логарифмической функции выводятся
из того, что она обратна показательной.
Показательная функция у а х Логарифмическая функция
у log а х
Область определения = R
Область определения = ( 0; +∞ )
Множество значений = ( 0; +∞ )
Множество значений = R
Возрастает при а>0, убывает
при 0<a<1
Возрастает при а>0, убывает
при 0<a<1
а⁰ = 1, à à
1
log a 1 0, log a a 1
3.
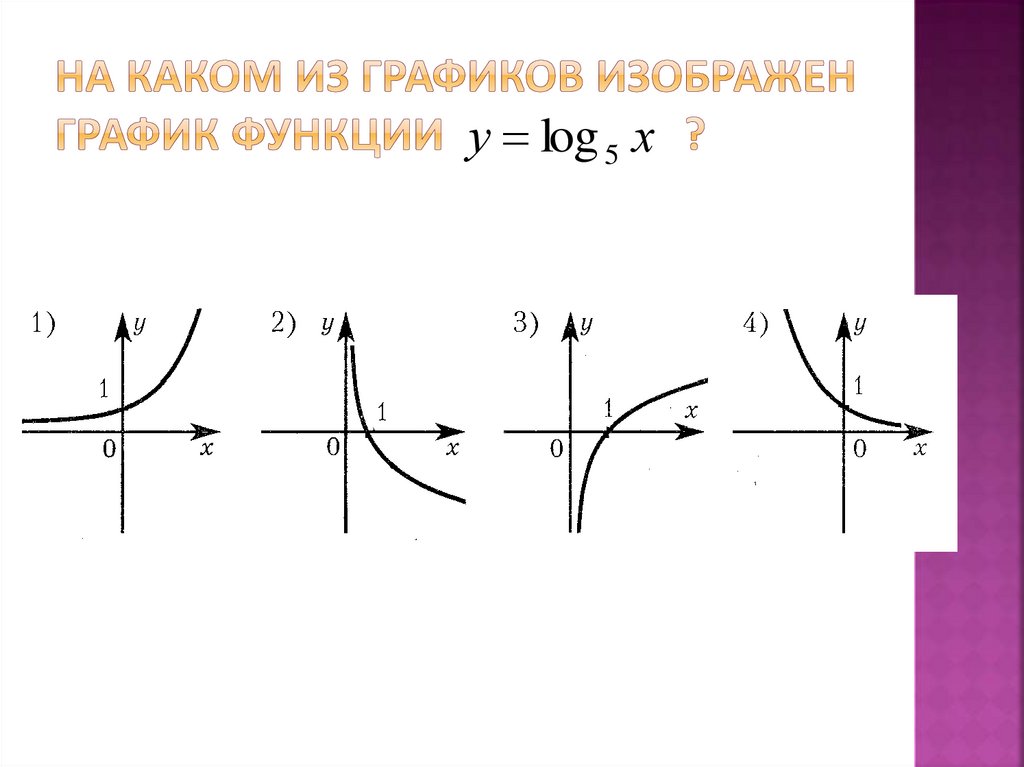
у log 5 х4.
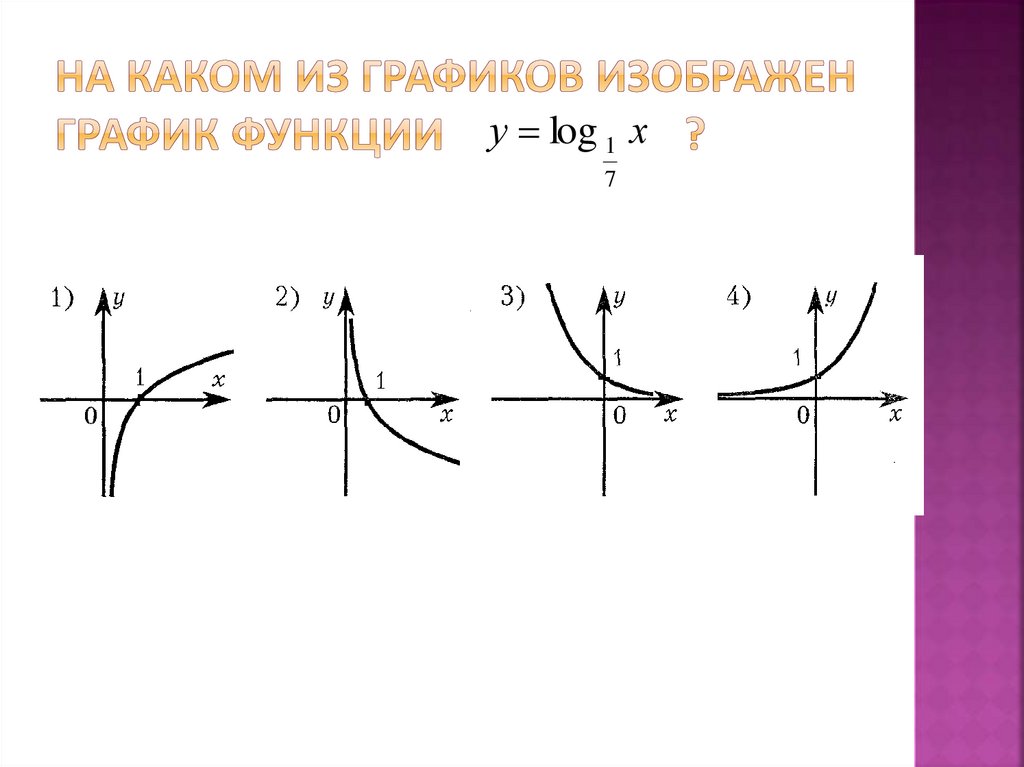
у log 1 х7
5.
6.
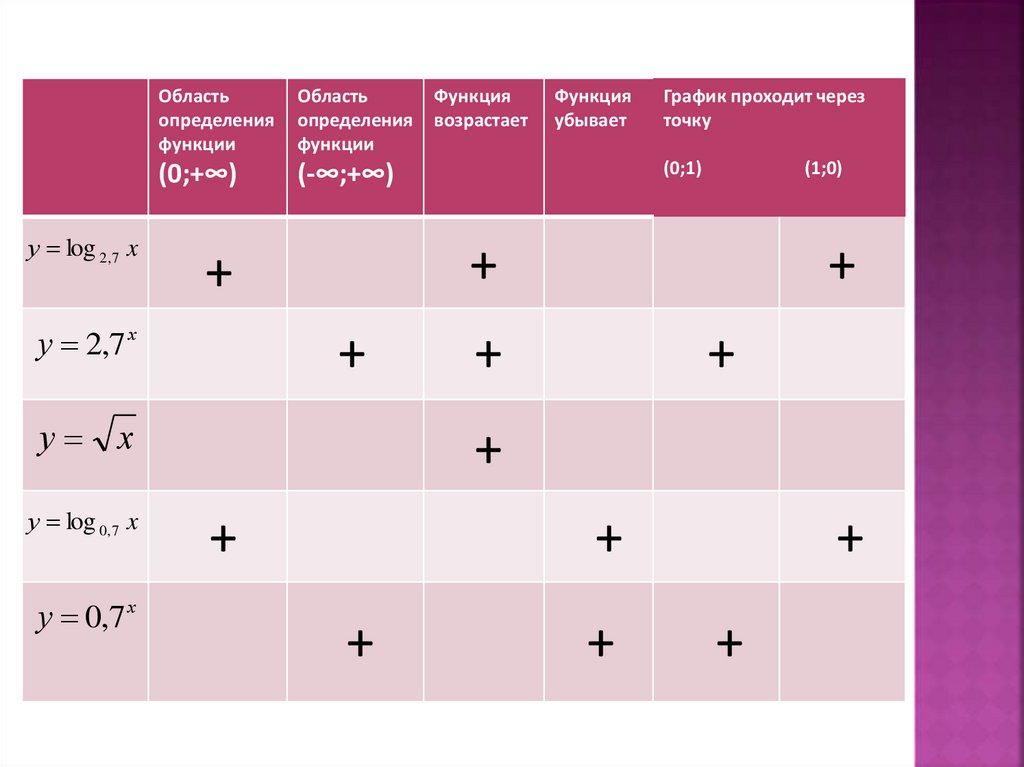
у log 2, 7 xОбласть
определения
функции
Область
определения
функции
(0;+∞)
(-∞;+∞)
+
у х
у log 0, 7 x
у 0,7 х
Функция
убывает
График проходит через
точку
(0;1)
(1;0)
+
+
у 2,7 х
Функция
возрастает
+
+
+
+
+
+
+
+
+
+
7.
Для решения логарифмических уравненийчасто используются свойства логарифмов.
Какие?
Как представить b число в виде логарифма по
основанию а ?
Равносильны ли уравнения
log a f ( x) log a g ( x) и f ( x) g ( x) ?
Как определить посторонний корень
уравнения?
Какие способы решения логарифмических
уравнений вы знаете?
8.
Первый вариантВторой вариант
1) log 0,5 ( x 1) 1
1) log 0, 2 (6 x ) 1
2) lg x lg x 0
2)
2
lg x lg x 0
2
9.
10.
log a f ( x) log a g ( x)1. Сравнить основание функции с единицей
и определить, возрастает или убывает
функция.
2. Записать систему неравенств, включая область
определения функций.
11.
log 1 ( x 5) 23
log 1 ( x 5) log 1 9
3
х 5 9
x 14
3
12.
Первый вариантВторой вариант
решите неравенство
решите неравенство
log 5 ( x) 0
log 0, 4 ( x) 0
13.
Первыйвариант:
21
у
log 2 х 2
(0;4) ; (4;+∞)
у 6 2 log 2 х
(0;4]
Второй
у
вариант
1
lg х 2
(0;0,01) ; (0,01; +∞)
у 8 3 log 4 х
(0;64]
14.
Уровень 1: решите уравнениеlog 2 ( x 3) 4
Уровень 2: решите уравнение
log 9 x 2 log 3 x 5
Уровень 3: найдите наибольший корень
уравнения
1
lg( x 6) 2 lg( 2 x 3) lg 25
2
15.
Галилео Галилей16.
Домашнее задание :тематические тренировочные
задания с.43 контрольная
работа № 3 вариант 1.
17.
18.
2 log 5 252 log 2 4
3 log 5 125
3 log 2 8
4 log 5 625
4 log 2 16
5 log 2 32
b log a a
b
19.
Уравнение решаетсяпо определению
логарифма;
Потенцированием;
Введением новой
переменной;
Логарифмированием;
Переходом к новому
основанию.
log 2 (3x 2) 1
log 2 (3x 2) log 2 (6 x)
3 log 3 x log 3 x 2 0
2
х
log2 x 1
8x
2
log 8 x log 4 x log 2 x 3
3














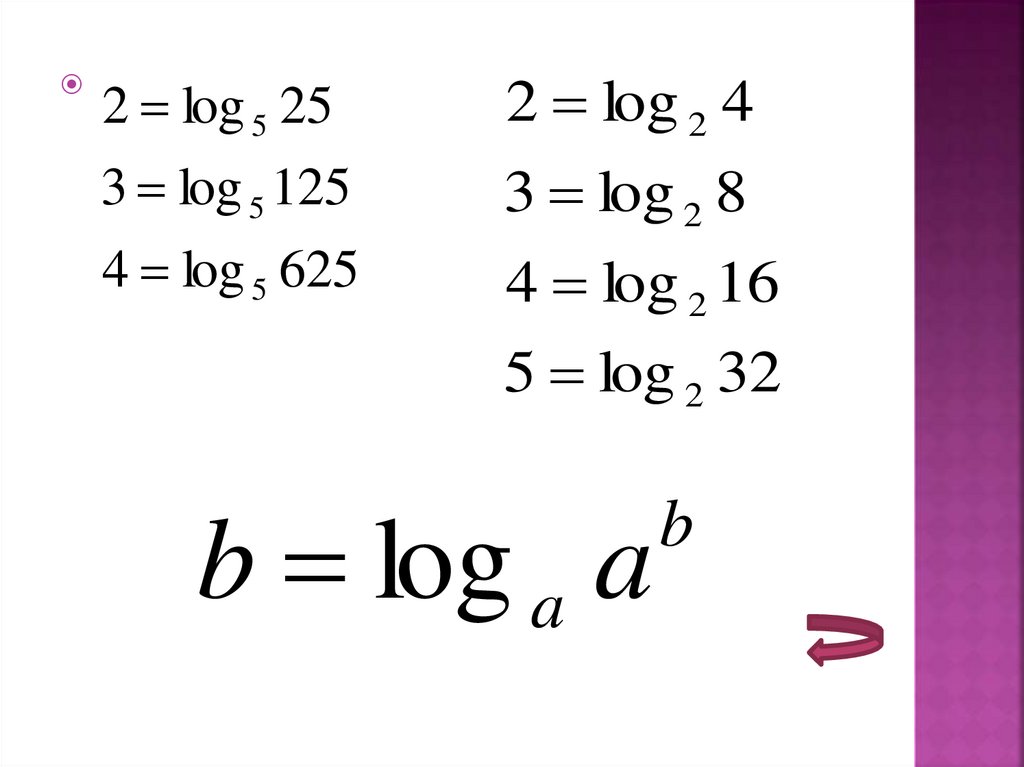

 Математика
Математика








