Похожие презентации:
Электронный справочник. Функции
1.
Электронныйсправочник.
2.
ФункцииСтепенные функции
Функция корня n-й степени, иррациональные уравнения и неравенства
Тригонометрические функции
Тригонометрические уравнения
Тригонометрические формулы
Тригонометрические неравенства
Показательная функция, уравнения, неравенства
Логарифмы, логарифмическая функция, уравнения,
неравенства
Производная
Применение производной функции
Первообразная функции и неопределенный интеграл
Определенный интеграл
3.
Логарифмы. Свойства логарифмов.Логарифмическая функция.
Свойства логарифмической функции.
Простейшие логарифмические
уравнения.
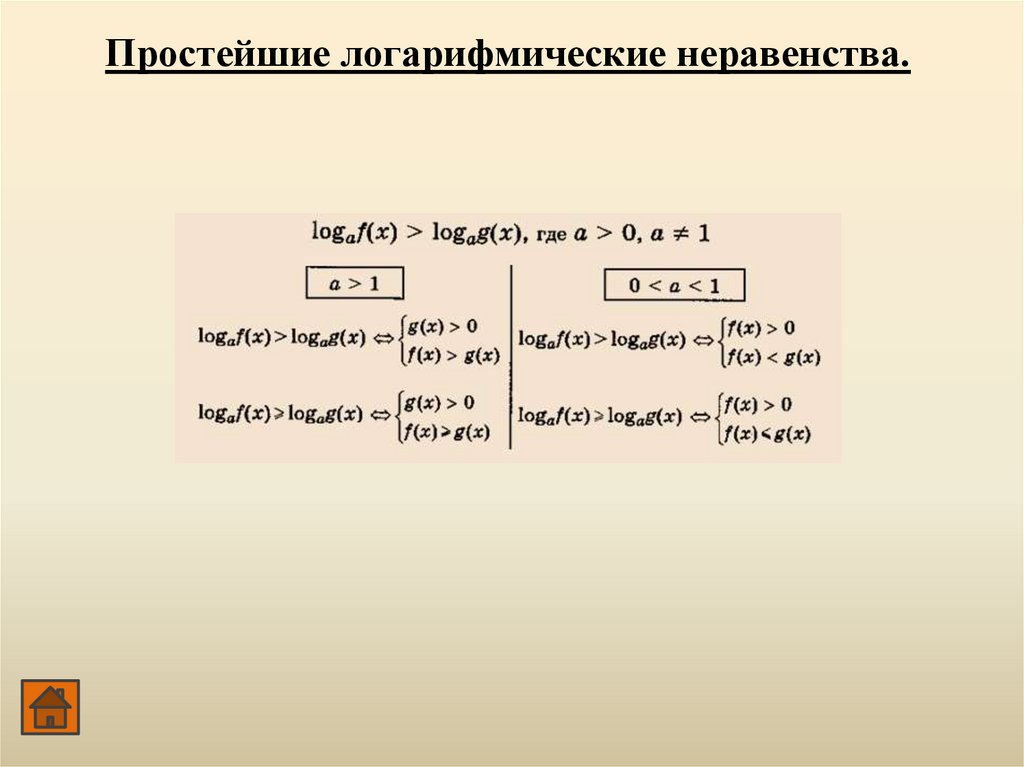
Простейшие логарифмические неравенства.
главная
4.
Логарифмы. Свойства логарифмов.a> 0, a≠1 , b> 0
a
loga b
b
основное
- логарифмическое
тождество
log a 1 0 log a a 1
log a b c log a b log a c
b
log a log a b log a c
c
1
log a b
log b a
log a b n n log a b
1
log a m b log a b
m
a
log cb
b
log c a
log c b
log a b
log c a
5.
Логарифмическая функция.y
y=logax, где a> 0, a≠1
a>1
1
x
a<1
6.
Свойства логарифмической функции.7.
Простейшие логарифмические уравнения.8.
Простейшие логарифмические неравенства.9.
Определенный интегралОсновные свойства определенного интеграла
Криволинейная трапеция
Площадь криволинейной трапеции
(формула Ньютона-Лейбница)
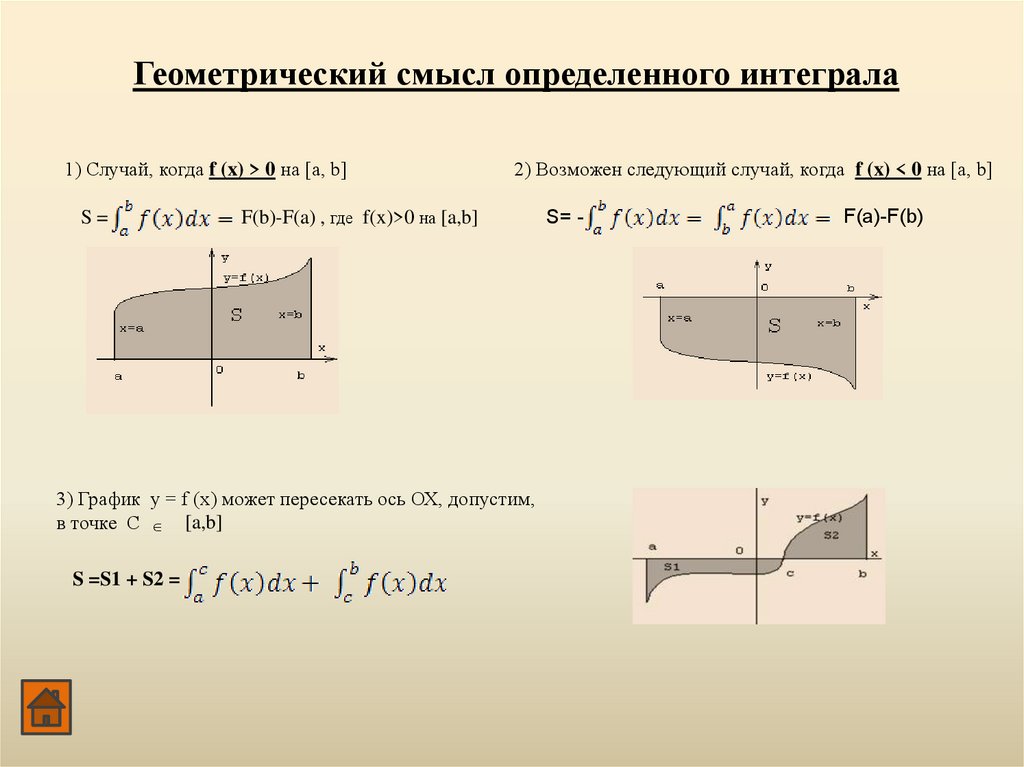
Геометрический смысл определенного интеграла
Физический смысл определенного интеграла
Вычисление площадей и объемов с помощью
определенного интеграла
главная
10.
Определенный интеграл11.
Основные свойства определенного интеграла12.
Криволинейная трапецияПусть на отрезке [a;b] оси ОХ задана непрерывная функция f (х), не меняющая на
нем знака. Фигуру, ограниченную графиком этой функции, отрезком [a;b] и
прямыми x = a и x = b, называют криволинейной трапецией.
Различные примеры криволинейных трапеций приведены на рис. 1, а — д.
13.
Площадь криволинейной трапеции(формула Ньютона-Лейбница)
Для вычисления площадей криволинейных
применяется формула Ньютона-Лейбница:
если F (х) — первообразная на отрезке [а; b], то
F(b) - F(a)
трапеций
14.
Геометрический смысл определенного интеграла1) Случай, когда f (x) > 0 на [а, b]
S=
2) Возможен следующий случай, когда f (x) < 0 на [а, b]
F(b)-F(a) , где f(x)>0 на [a,b]
3) График y = f (x) может пересекать ось ОХ, допустим,
в точке С [a,b]
S =S1 + S2 =
S= -
F(a)-F(b)
15.
Физический смысл определенного интегралаПри прямом движении перемещение s
численно равно площади криволинейной трапеции
под графиком зависимости ν от времени t:
16.
Вычисление площадей и объемовс помощью определенного интеграла
Площадь фигуры
Объем тела
17.
Первообразная функции.Основное свойство первообразных.
Правила вычисления первообразной функции
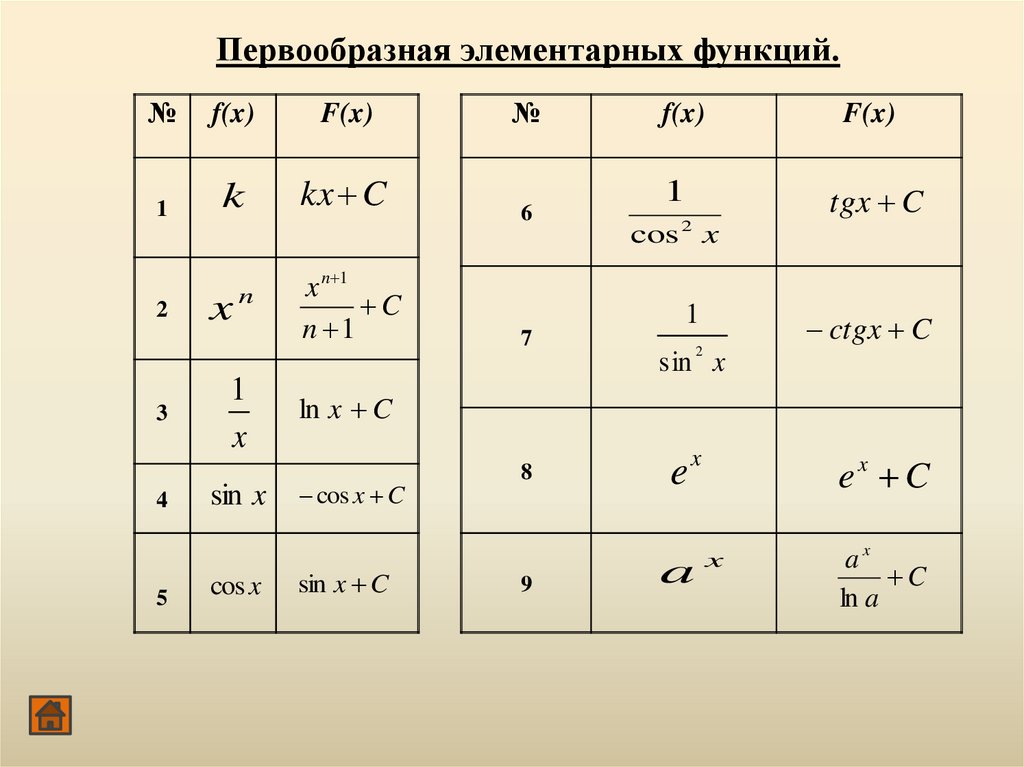
Первообразная элементарных функций.
Неопределенный интеграл.
Правила интегрирования.
Таблица интегралов.
главная
18.
Первообразная функции.Функция F (x) называется первообразной для функции f(x)
на данном промежутке, если для любого x из этого
промежутка F x f x
Основное свойство первообразных.
19.
Правила вычисления первообразной функции.Функция
Первообразная
k f x
k F x
f 1 x f 2 x
F1 x F2 x
f ax b
1
F ax b
a
20.
Первообразная элементарных функций.№
f(x)
F(x)
1
k
kx C
2
3
4
5
xn
1
x
sin x
cos x
x n 1
C
n 1
№
6
f(x)
1
F(x)
tgx C
2
cos x
1
7
ctgx C
2
sin x
ln x C
cos x C
sin x C
8
9
e
x
a
ex C
x
ax
C
ln a
21.
Неопределенный интеграл.Совокупность всех первообразных данной
функции f(x) называется ее неопределенным
интегралом и обозначается
∫f(x) dx = F(x) + C, где С – произвольная
постоянная.
22.
Правила интегрирования.∫cf(x)dx = c ∫f(x)dx, где с - const
∫(f(x) + g(x))dx = ∫f(x) dx + ∫g(x)dx
∫(f(x) - g(x))dx = ∫f(x) dx - ∫g(x)dx
1
∫f(ax + b)dx = F ax b С, где а=0
a
23.
Таблица интегралов.24.
Показательная функцияСвойства показательной функции
Простейшие показательные уравнения
Простейшие показательные неравенства
главная
25.
Показательная функцияЗамечание:
26.
Свойства показательной функции27.
Простейшие показательные уравнения28.
Простейшие показательные неравенства29.
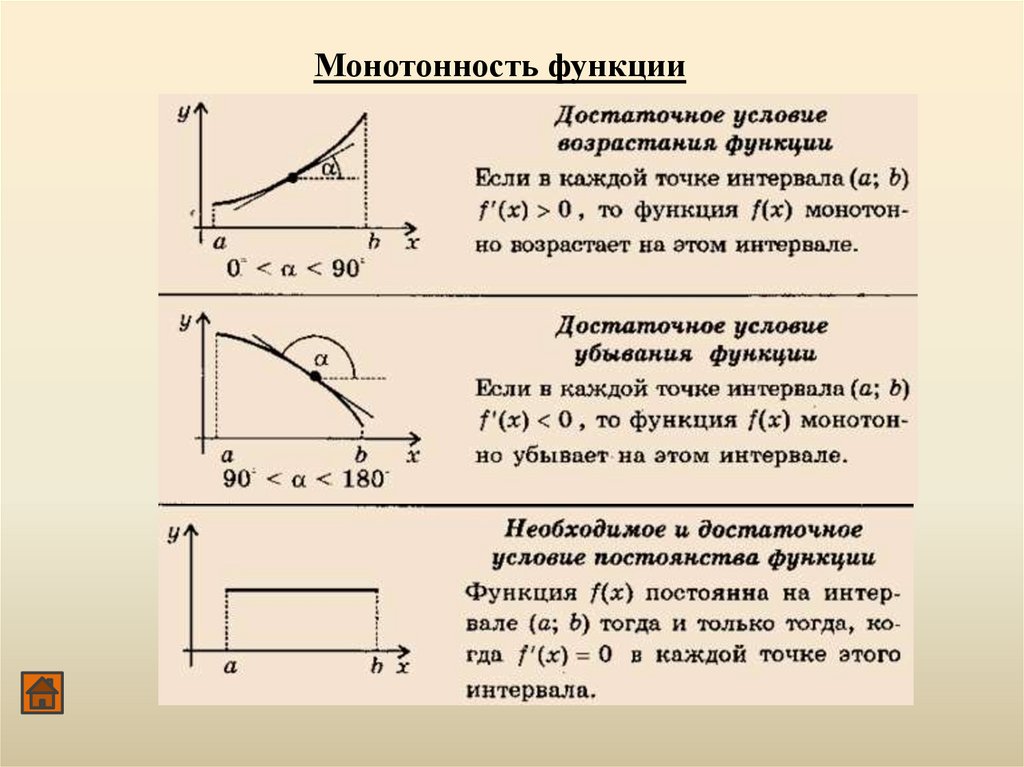
Монотонность функцииЭкстремумы функции
Примеры экстремумов функции
Наибольшее и наименьшее значения
функции, непрерывной на отрезке
главная
30.
Монотонность функции31.
Экстремумы функцииНеобходимое условие экстремума:
Достаточное условие экстремума:
32.
Примеры экстремумов функции33.
Наибольшее и наименьшее значения функции,непрерывной на отрезке
34.
Производная функцииГеометрический смысл производной функции
Физический смысл производной функции
Уравнение касательной
Правила дифференцирования и производная сложной функции
Производные элементарных функций
главная
35.
Производная функцииПроизводной функции f(x) в точке x0 называется предел
отношения приращения функции ∆f=f(x0+ ∆x)-f(x0) к
приращению аргумента ∆x при ∆x 0, если этот предел
существует:
f΄(x0) = lim
∆x
0
f(x0 + ∆x) – f(x0)
∆x
36.
Геометрический смысл производной функции37.
Физический смысл производной функции38.
Уравнение касательной39.
Правила дифференцирования(C)' 0
C u
u v
C u
u v ' u' v'
u v u v
u
v u v
u
2
v
v
Производная сложной функции
y f x y f
'
'
x
40.
Производные элементарных функций№
Функция
Производная
№
1
xn
nx n 1
6
2
sin x
3
4
5
cos x
tgx
ctgx
cos x
Функция
Производная
ex
ex
7
ax
a x ln a
8
ln x
9
loga x
sin x
1
cos2 x
1
sin2 x
1
x
1
x ln a
41.
Степенные функции с натуральными показателями степени• свойства функции
Степенные функции с целыми отрицательными показателями
степени
• свойства функции
Степенные функции с действительными показателями
степени
• свойства функции
главная
42.
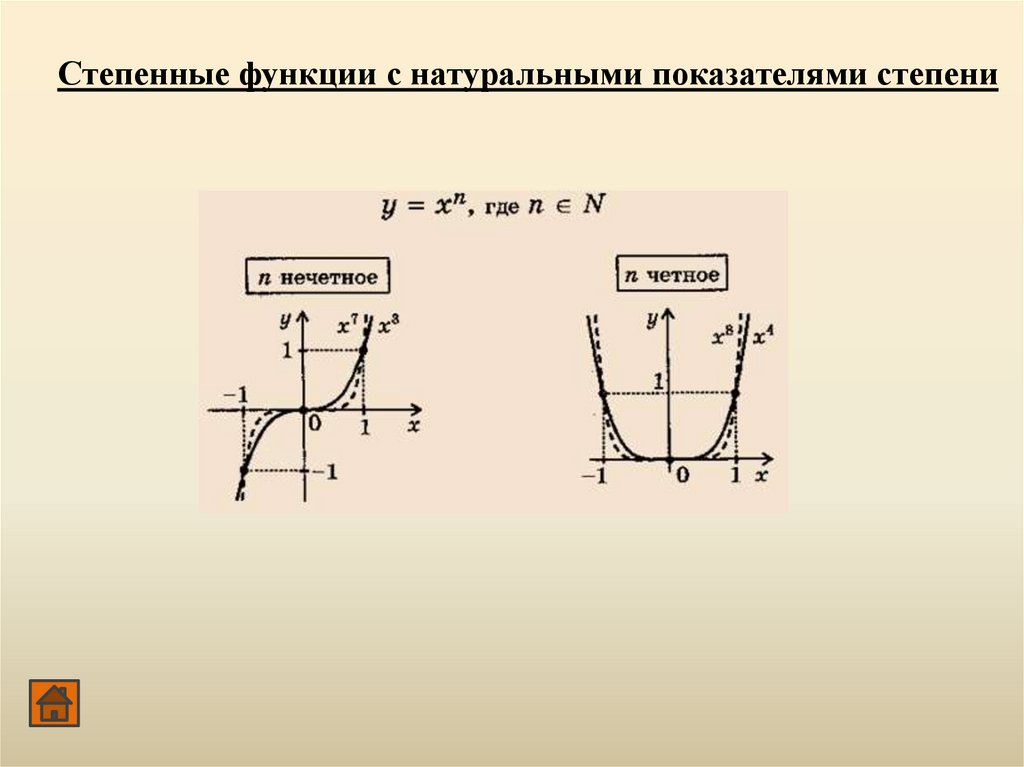
Степенные функции с натуральными показателями степени43.
Свойства функцииЗамечание: при n=0 функция y=xn определяется так:
x0=1 при x=0 ; при x=0 функция не определена.
44.
Степенные функциис целыми отрицательными показателями степени
45.
Свойства функцииЗамечание: при n=1 функция y=x-n имеет вид y=1/x и
называется обратной пропорциональностью.
46.
Степенные функциис действительными показателями степени
47.
Свойства функции48.
sin x > a; sin x ≥ a; sin x < a; sin x ≤ acos x > a; cos x ≥ a; cos x < a; cos x ≤ a
tg x > a; tg x ≥ a; tg x < a; tg x ≤ a
ctg x > a; ctg x ≥ a; ctg x < a; ctg x ≤ a
главная
49.
sin x > a; sin x ≥ a; sin x < a; sin x ≤ a50.
cos x > a; cos x ≥ a; cos x < a; cos x ≤ a51.
tg x > a; tg x ≥ a; tg x < a; tg x ≤ a52.
ctg x > a; ctg x ≥ a; ctg x < a; ctg x ≤ a53.
Основное тригонометрическое тождество иследствия из него
Формулы двойного угла
Формулы половинного аргумента
Формулы обратных тригонометрических функций
Формулы произведения функций
Формулы суммы аргументов
Формулы тройных углов
Формулы понижения степени
Универсальная тригонометрическая подстановка
главная
54.
Основное тригонометрическое тождество и следствия из него1. sin 2 cos 2 1
2. 1 tg
2
1
;
cos
1
2
3. 1 ctg
;
2
sin
2
4. tg ctg 1;
n, n Z
2
n, n Z
n
, n Z
2
55.
Формулы двойного аргументаsin 2 2 sin cos
cos 2 cos sin 2 cos 1 1 2 sin
2
2
2
2tg
tg 2
2
1 tg
2
56.
Формулы половинного аргумента1 cos
sin
2
2
2
1 cos
cos
2
2
2
sin
1 cos
tg
2 1 cos
sin
57.
Формулы обратных тригонометрических функцийarcsin x arccos x
arctgx arcctgx
Если 0 < x 1, то
arccos(-x) = - arccosx
arcsin(-x) = - arcsinx
2
2
Если x > 0 , то
arctg(-x) = - arctgx
arcctg(-x) = - arcctgx
58.
Формулы произведения функций1
sin sin cos cos
2
1
cos cos cos cos
2
1
sin cos sin sin
2
59.
Формулы суммы аргументовsin sin cos cos sin
sin sin cos cos sin
cos cos cos sin sin
cos cos cos sin sin
tg tg
tg
1 tg tg
tg tg
tg
1 tg tg
60.
Формулы тройных угловsin 3 3 sin 4 sin
3
3tg tg
tg 3
2
1 3tg
3
cos 3 4 cos 3 cos
3
ctg 3ctg
ctg 3
2
3ctg 1
3
61.
Формулы понижения степени1.
2.
3.
4.
1
sin 1 cos 2
2
1
2
cos 1 cos 2
2
1 cos 2
2
tg
1 cos 2
1 cos 2
2
ctg
1 cos 2
2
62.
Универсальная тригонометрическая подстановка2tg
1. sin
1 tg
2. cos
2
2
2
1 tg
2
1 tg
2
2 ; 2 n, n Z
2
63.
Уравнение cosx=a
Уравнение sinx
главная
=a
Уравнение
tg х = а
Уравнение
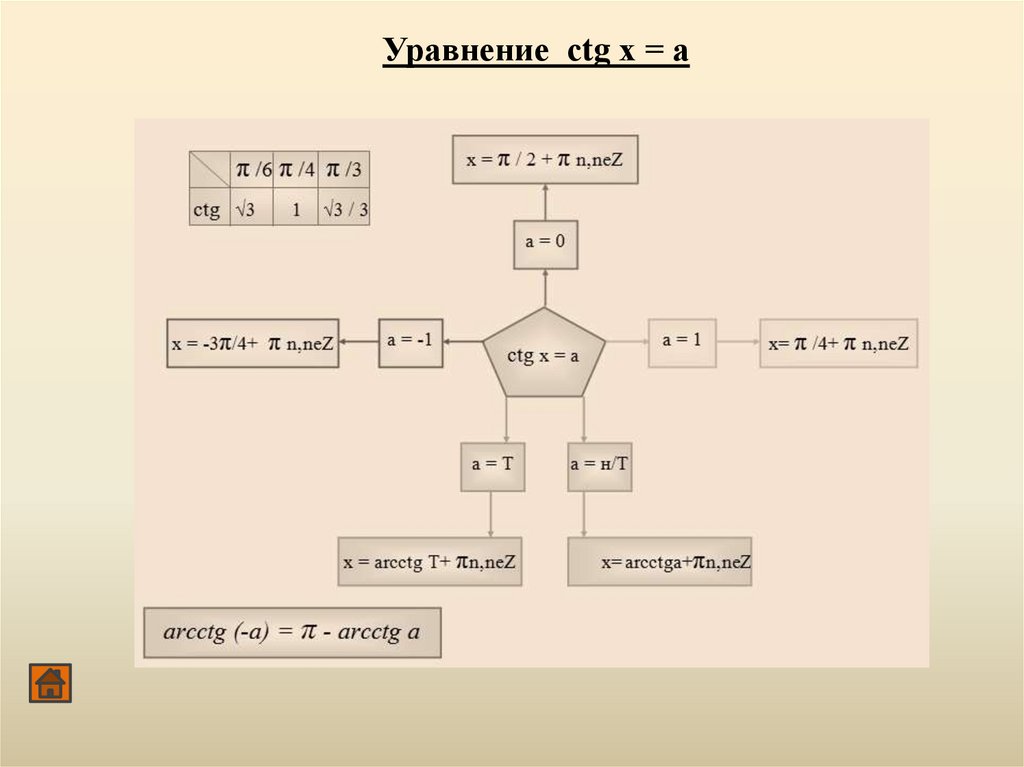
сtg х = а
64.
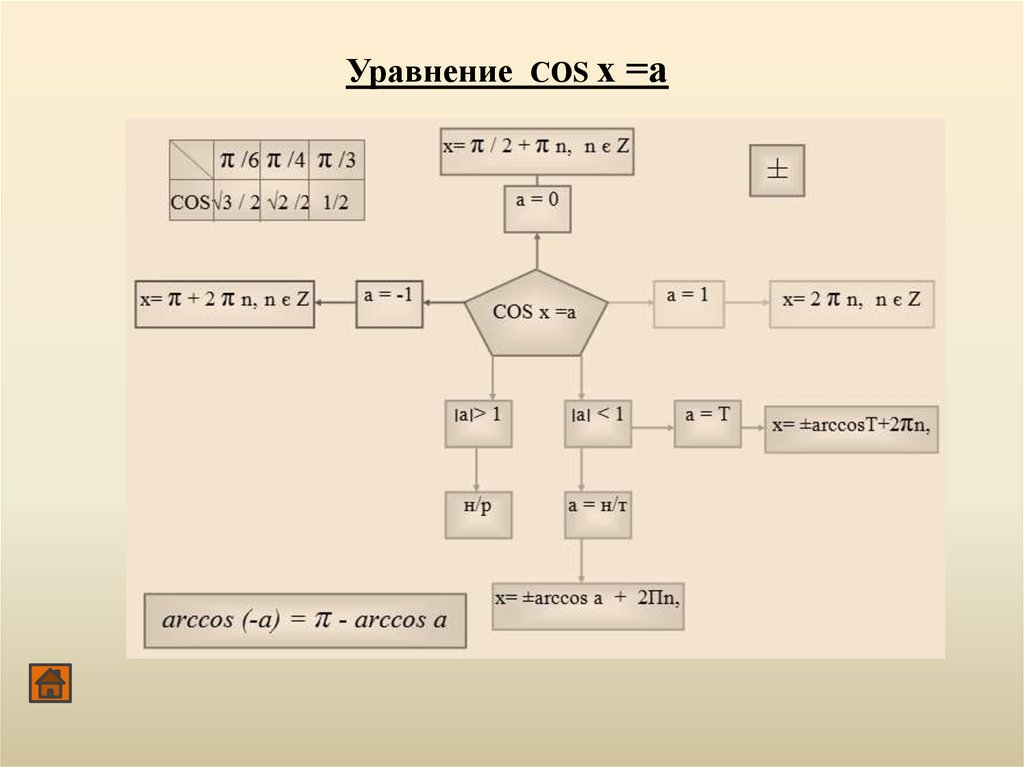
Уравнение СОS х =а65.
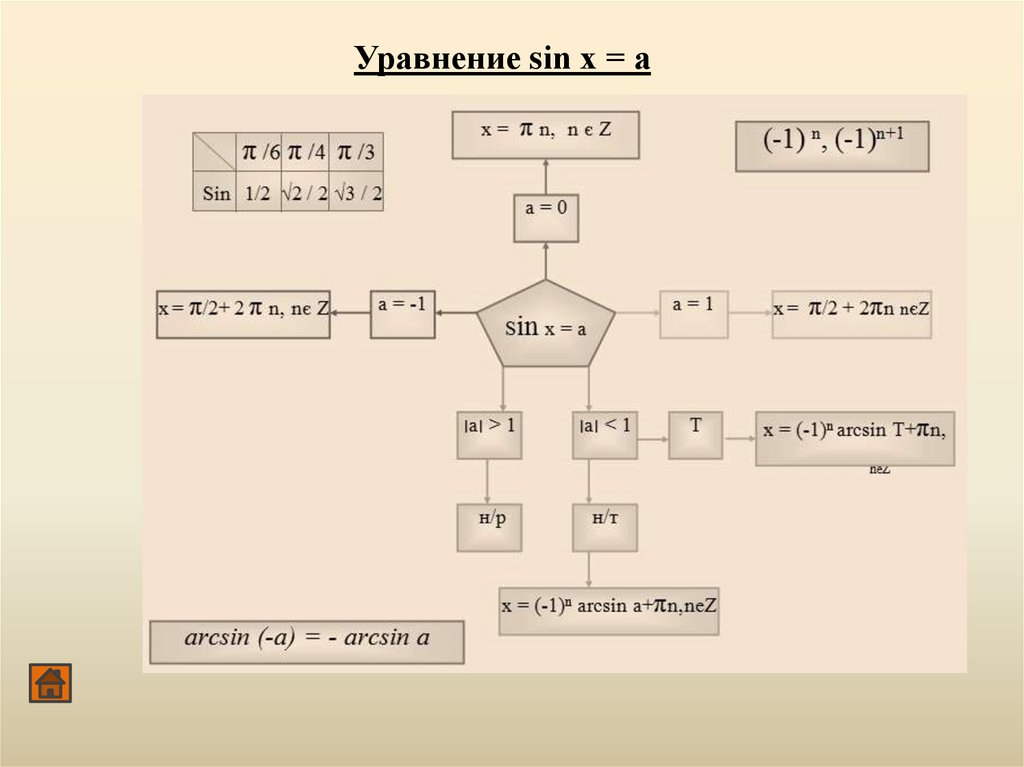
Уравнение sin х = а66.
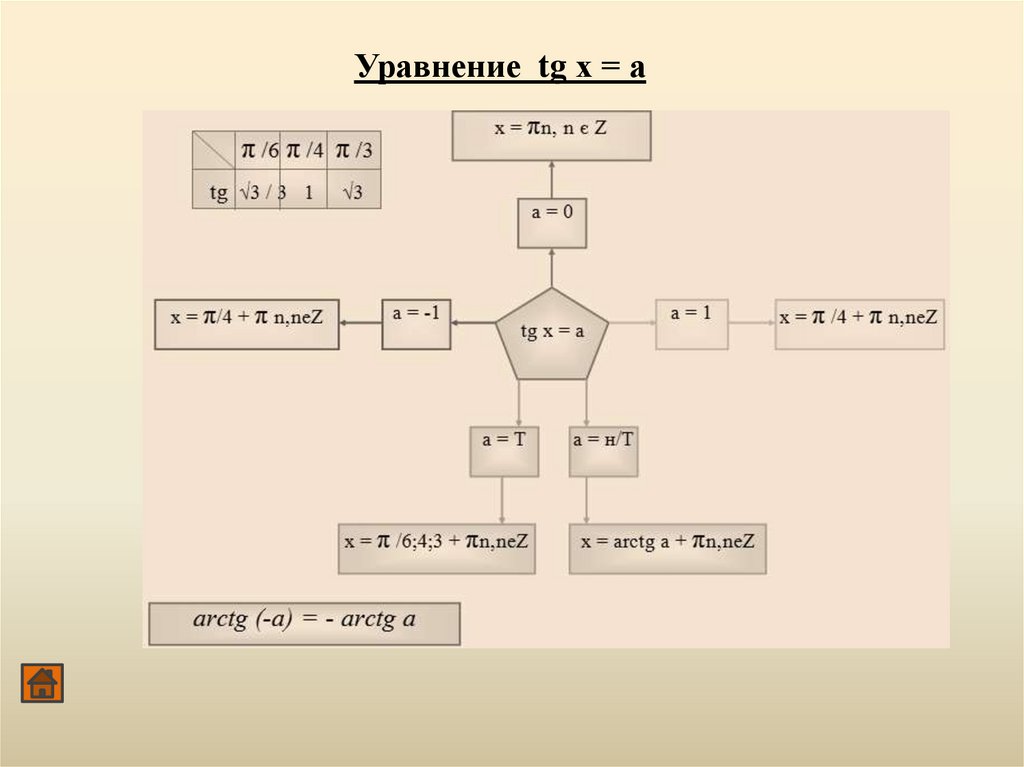
Уравнение tg х = а67.
Уравнение сtg х = а68.
Определение тригонометрических функций:•Синус и косинус
•Тангенс и котангенс
Графики тригонометрических функций:
• Синус • Тангенс и котангенс
• Косинус
Свойства синуса и косинуса
Свойства тангенса и котангенса
Обратные тригонометрические функции
Связь между тригонометрическими функциями
одного аргумента
Значения тригонометрических функций некоторых
углов
главная
69.
Определение тригонометрических функцийФункция косинус — это функция, которая ставит в
соответствие каждому числу t абсциссу точки М(t)
координатной окружности.
у
М(t)
sin t
t
Функция синус — это функция, которая ставит в
соответствие каждому числу t ординату точки М(t)
координатной окружности.
Если М(t) = М(х; у),
то х = cos t, у = sin t
Таким образом,
М(t) = М(cos t; sin t)
Запись М(t) показывает положение точки М на координатной окружности,
а запись М(cos t; sin t) – положение той же точки на координатной плоскости.
cos t
х
70.
Функция тангенс —это частное от деления функции
синус на функцию косинус.
Функция котангенс —
это частное от деления функции
косинус на функцию синус.
Поскольку деление на нуль невозможно, функции tg t и ctg t определены
не для всех значений аргумента. Тангенс определен лишь для значений
аргумента, при которых cos t 0, котангенс определен при sin t 0:
sin t
, где
cos t
cos t
сtg t
, где
sin t
tg t
t
k , k Z
2
t k , k Z
71.
Графики тригонометрических функцийу = sin x
синусоида
у
1
–2
3π
2
–
π
2
π
2
–1
3π
2
2
5π
2
х
72.
ко синусоидау = cos x
у
1
–2
3π
2
–
π
2
π
2
–1
3π
2
2
5π
2
х
73.
у = tg xтангенсоида
у = ctg x
ко тангенсоида
у
у
2
2
1
1
–
π
2
–1
–2
π
2
х
π
2
–1
–2
π
2
3π
2
х
74.
Свойства синуса и косинуса75.
Свойства тангенса и котангенса76.
Обратные тригонометрические функции77.
Связь между тригонометрическими функциямиодного аргумента
78.
Значения тригонометрических функций некоторых углов79.
ФункцииЧетность и нечетность
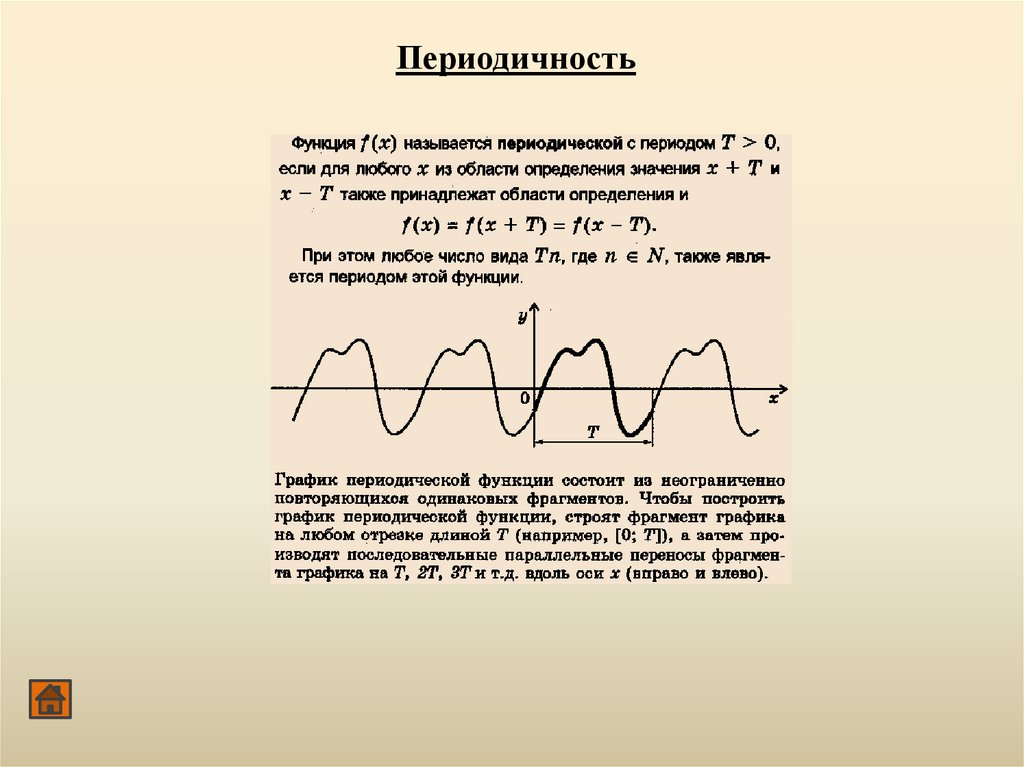
Периодичность
Нули функции
Монотонность
Экстремумы
Асимптоты
Обратные функции
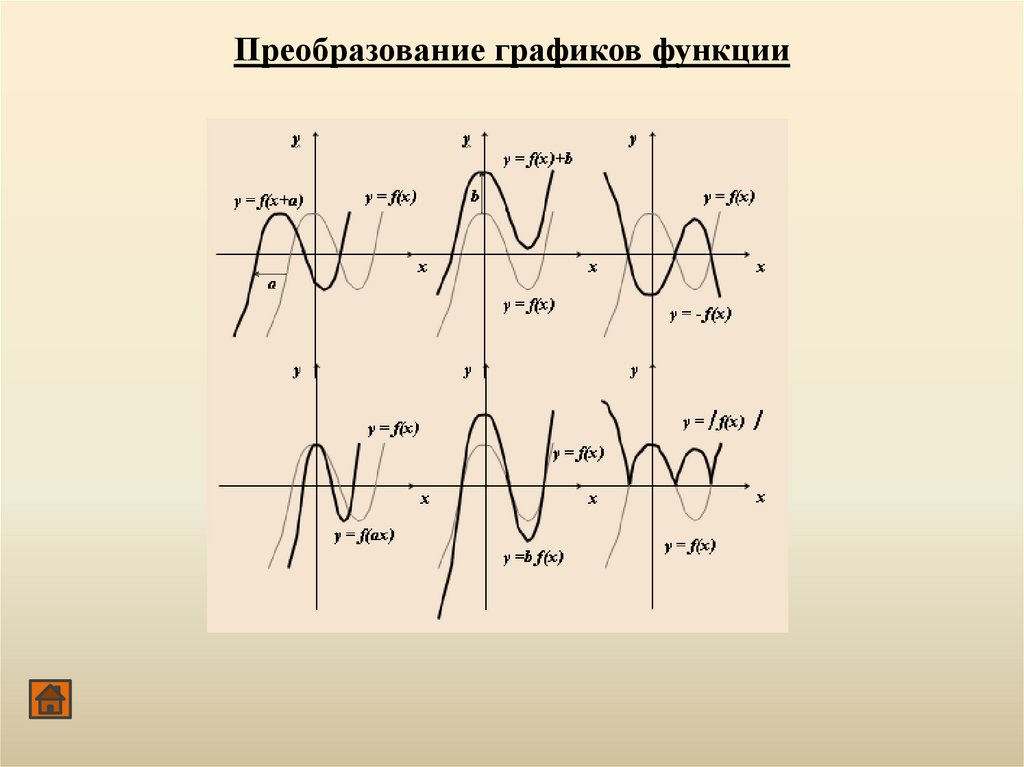
Преобразование графиков функции
Свойства элементарных функций
главная
80.
Функции81.
Четность и нечетность82.
Периодичность83.
Нули функции84.
Монотонность85.
Экстремумы86.
Асимптоты87.
Обратные функцииНахождение формулы для функции, обратной данной:
Пользуясь формулой y=f(x), следует выразить x через y, а
в полученной формуле x=g(y) заменить x на y, а y на x.
88.
Преобразование графиков функции89.
Свойства элементарных функций90.
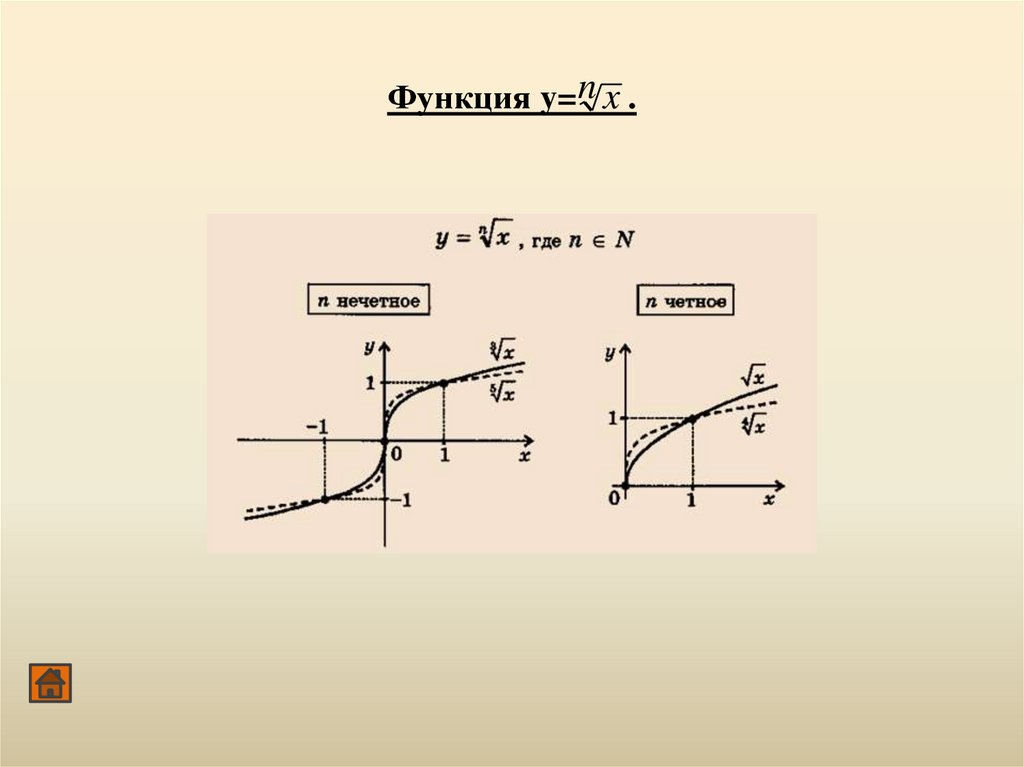
Функция y= n x .• свойства функции
Иррациональные уравнения.
Иррациональные неравенства.
главная
91.
Функция y=n x .92.
Свойства функции93.
Иррациональные уравнения.Как правило иррациональное уравнение сводиться к равносильной системе,
содержащей уравнения и неравенства.
Замечание. Из двух систем выбирают ту, которая решается проще.
94.
Иррациональные неравенства.Как правило иррациональное неравенство сводиться
к равносильной системе (или совокупности систем) неравенств.


















































































 Математика
Математика








