Похожие презентации:
Интегрирование функции одной переменной
1. Неопределенный интеграл
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ2. Элементы интегрального исчисления
ЭЛЕМЕНТЫ ИНТЕГРАЛЬНОГОИСЧИСЛЕНИЯ
1.Первообразная и неопределенный интеграл
2.Своства интеграла, вытекающие из
определения
3.Свойства интеграла
4. Таблица интегралов
5. Свойства дифференциалов
6. Методы интегрирования
7. Разложение полиномов на сомножители
8. Интегрирование дробно-рациональных
функций
9. Интегрирование тригонометрических
функций
3.
ПЕРВООБРАЗНАЯ ИНЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Пусть X R.
Определение. Функция F(x), x X называется первообразной для функции y = f(x) на множестве X если она
дифференцируема в каждой точке этого множества и F'(x)=f(x).
Теорема. Любая непрерывная на отрезке [a, b] функция
y=f(x) имеет на этом отрезке первообразную F(x).
Теорема. Если F1(x) и F2(x) – две различные
первообразные одной и той же функции f(x) на множестве X, то
они отличаются друг от друга постоянным слагаемым, т.е.
F2(x) = F1(x) + С, где С – константа.
4.
Определение. Совокупность F(x) + С всех первообраных функции y = f(x) на множестве X называетсянеопределенным интегралом функции y = f(x).
Обозначение. f ( x ) dx
при этом f(x) называют подынтегральная функция,
f(x) dx – подынтегральное выражение,
а – знак интеграла.
С геометрической точки зрения неопределенный
интеграл представляет собой однопараметрическое
семейство кривых y = F(x) + С (С – параметр),
обладающих следующим свойством: все касательные к
кривой в точках с абсциссой x = x0 параллельны между
собой.
5. Свойства интегралов, вытекающие из определения
СВОЙСТВА ИНТЕГРАЛОВ, ВЫТЕКАЮЩИЕИЗ ОПРЕДЕЛЕНИЯ
Производная неопределенного интеграла равна
подынтегральной функции, а его дифференциал подынтегральному выражению.
1. ( f ( x)dx) ( F ( x) C ) F ( x) f ( x);
2. d f ( x)dx ( f ( x)dx) dx f ( x)dx.
Неопределенный интеграл от дифференциала непрерывно
дифференцируемой функции равен самой этой функции с точностью
до постоянной:
3.
d ( x) ( x)dx ( x) C,
так как (x )
является первообразной для (x).
6. Свойства интегралов
СВОЙСТВА ИНТЕГРАЛОВСформулируем далее следующие свойства
неопределенного интеграла:
4. Если функции f1 x и f 2 x имеют
первообразные, то функция f1 x f 2 x
также имеет первообразную, причем
f1 x f 2 x dx f1 x dx f 2 x dx ;
5. Kf x dx K f x dx ;
6. f x dx f x C ;
7. f x x dx F x C .
8. Если f x dx F x C , то
f x b dx F x b C .
9. Если f x dx F x C , то
1
f ax b dx F ax b C .
a
7. Таблица неопределенных интегралов
ТАБЛИЦА НЕОПРЕДЕЛЕННЫХИНТЕГРАЛОВ
1. dx x C .
x a 1
2. x dx
C, (a 1) .
a 1
dx
3. ln x C .
x
x
a
4. a x dx
C .
ln a
a
5. e x dx e x C .
6. sin xdx cos x C .
7. cos xdx sin x C .
dx
8. 2 ctgx C .
sin x
dx
9. 2 tgx C .
cos x
dx
arctgx C .
10.
2
1 x
8.
11.dx
arcsin x C .
1 x 2
dx
1
x
12. 2 2 arctg C .
a
a
a x
13.
a2 x2
arcsin
x
C .
a
x2 a
ln x x 2 a C .
17. shxdx chx C .
18. chxdx shx C .
dx
1
x a
ln
C
2
2
2a x a
x a
19.
dx
1
a x
ln
a 2 x 2 2a a x C .
20.
14.
15.
dx
dx
16.
dx
ch 2 x thx C .
dx
cthx C .
2
sh x
9. Свойства дифференциалов
СВОЙСТВА ДИФФЕРЕНЦИАЛОВПри интегрировании удобно пользоваться
свойствами:
1
1. dx d (ax)
a
1
2. dx d (ax b),
a
1 2
3. xdx dx ,
2
1 3
2
4. x dx dx .
3
10.
Во всех формулах этой таблицы в качестве и можно брать произвольнуюдифференцируемую функцию и = (х).
n 1
u
n
1. d
u
du
n 1
7.
d (tgu)
2. d ln u du
8.
d (ctgu)
du
sin 2 u
3. d (eu ) eu du
9.
d arcsin u
du
du
cos2 u
u
au
u
d
ln a
a du
10.
5. d (sin u) cosudu
11.
6. d (cosu) sin udu
12.
4.
1 u2
d arccosu
du
1 u2
du
d arctgu
1 u2
du
d arcctgu
1 u2
11. Пример
ПРИМЕРПример . Вычислить cos 5xdx .
Решение. В таблице интегралов найдем
cos xdx sin x C .
Преобразуем данный интеграл к табличному,
воспользовавшись тем, что d ax adx .
Тогда:
d 5 x 1
= cos 5 xd 5 x =
cos 5xdx cos 5 x
5
5
1
= sin 5 x C .
5
12. Методы интегрирования
МЕТОДЫ ИНТЕГРИРОВАНИЯ13.
МЕТОДЫ ИНТЕГРИРОВАНИЯ1. Непосредственное интегрирование – интегрирование с помощью
свойств, тождественных преобразований подынтегральной функции и
таблицы основных интегралов.
Пример. Вычислить x 2 3x 3 x 1 dx .
Решение. Так как под знаком интеграла находится сумма четырех
слагаемых, то раскладываем интеграл на сумму четырех
интегралов:
2 3x3 x 1 dx x 2 dx 3 x3dx xdx dx .
x
x4 x2
x3
x C
3
2
4
3
14.
2. Интегрирование разложением. Интегрирование разложением естьприведение данного интеграла к сумме более простых интегралов.
x4
Пример. Вычислить
dx
2
1 x
Решение.
x4
x4 1 1
1 x 2 dx x 2 1 dx
x 1 x 1 dx
2
2
x 1
2
1
1
2
x2 1 dx x 1 dx x2 1 dx
3
1
x
x 2 dx dx 2 dx x arctgx C
3
x 1
15.
2. Интегрирование по частям.Теорема. Если функции u(x) и v(x) дифференцируемы на некотором промежутке
и на этом промежутке существует интеграл vdu , то на нем существует и
интеграл udv , причем udv uv vdu
Методом интегрирования по частям берут такие интегралы:
а) x n sin xdx , где n 1,2...k ;
б) x n e x dx , где n 1,2...k ;
n
x arctgxdx , где n 0, 1, 2,... k . ;
г) x n ln xdx , где n 0, 1, 2,... k .
в)
При вычислении интегралов а) и б) вводят обозначения: x
n
u , тогда
du nx n 1dx , а, например sin xdx dv ,тогда v cos x .
При вычислении интегралов в), г) обозначают за u функцию arctgx , ln x , а за
dv берут x n dx .
16. Пример
ПРИМЕРПример. Вычислить x cos xdx .
Решение.
u x, du dx
=
x cos xdx
dv cos xdx, v sin x
x sin x sin xdx x sin x cos x C .
17. Примеры
ПРИМЕРЫПример. Вычислить
x ln xdx
dx
u ln x, du
x
x2
dv xdx, v
2
x2
x 2 dx
=
ln x
2
2 x
x2
1
x2
1 x2
=
ln x xdx
ln x
C .
2
2
2
2 2
18.
3. Замена переменной. Метод заключается в переходе к новомуаргументу интегрирования путём преобразования подынтегрального
выражения по некоторой формуле.
x (t )
f ( x)dx
f ( (t )) (t )dt.
dx (t )dt
При этом говорят, что в интеграле слева сделана замена переменной
(подстановка) по формуле x (t ).
После вычисления интеграла справа необходимо в ответе вернуться снова
к аргументу x, выразив t в формуле x (t ) через х.
Пример. Вычислить
x 6t
x
x
cos 6 dx dx 6 dt cos t 6 dt 6 cos t dt 6 sin t C t 6
x
6 sin C.
6
19.
Замечание. Используя простейшую замену переменной, легкополучить следующие формулы:
n 1
1
(
ax
b
)
(ax b) n dx
C (n 1)
a
n 1
1
1
dx ln | ax b | C
ax b
a
1 ax
e dx
e C
a
ax
1
sin ax dx cos ax C
a
1
cos ax dx sin ax C
a
20. Пример
ПРИМЕРВычислим
1
6
(
2
3
x
)
dx
(
2
3
x
)
C.
3 6
5
21.
РАЗЛОЖЕНИЕ ПОЛИНОМОВНА
СОМНОЖИТЕЛИ
Определение. Число b (действительное или комплексное) называется
корнем полинома Pn(x), если Pn(b) = 0.
Теорема 1. Для того, чтобы b было корнем полинома Pn(x), необходимо и
достаточно, чтобы Pn(x) делилось на (x – b).
Теорема 2. Пусть корень полинома b есть комплексное число. Тогда
комплексно сопряженное число
также является корнем этого
полинома.
Основная теорема алгебры. Всякий полином степени п 1 имеет хотя
бы один корень (действительный или комплексный).
Теорема 3. Полином степени п имеет ровно п корней.
Определение. Если в разложении Pn(x) на сомножители бином (x – b)
повторяется k раз, то говорят, что корень b имеет кратность k.
Если k = 1, то корень называется простым.
Заметим еще, что в паре комплексно сопряженных корней оба корня
имеют одинаковую кратность.
22.
ИНТЕГРИРОВАНИЕ ДРОБНОРАЦИОНАЛЬНЫХ ФУНКЦИЙРациональной дробью называется дробь вида Pm(x) /Qn(x), где
Pm(x) и Qn(x) – многочлены степени т и п соответственно.
Рациональная дробь называется правильной, если степень числителя
меньше степени знаменателя (т < п), в противном случае дробь
называется неправильной.
Простейшими элементарными дробями называются дроби
следующего вида:
1.
2.
3.
4.
A;
x a
, m > 1, целое;
A
( x a) m
Ax B
, где квадратный
2
x px q
Ax B
2
( x px q) k
трехчлен не имеет действительных корней;
, где квадратный трехчлен не имеет действительных корней.
23.
Теорема. Пусть Pm(x) /Qn(x) правильная рациональная дробь, знаменателькоторой представлен в виде произведения линейных и квадратичных множителей
(с вещественными коэффициентами)
Qn(x) = a (x x1) (x x2) …(x2 + p x + q) … (x2 + r x + s) ,
где x1, x2,… вещественные корни, (x2 + p x + q), … (x2 + r x + s) квадратные
трехчлены, не разложимые на вещественные множители ( +…+ + +…+ = n ).
Тогда имеет место разложение
B
Pm ( x)
A1
A2
A
B1
B2
...
...
...
2
2
Qn ( x) x x1 ( x x1 )
( x x1 ) ( x x2 ) ( x x2 )
( x x2 )
R x S
M 1 x N1
M 1 x N 1
M x N
...
...
,
2
2
1
2
2
( x px q)
( x px q)
( x px q)
( x rx s)
где Ai , Bi , Mi , Ni , Ri , Si , … вещественные числа (некоторые из которых могут
быть равны нулю).
24.
АЛГОРИТМ ИНТЕГРИРОВАНИЯДРОБНО-РАЦИОНАЛЬНОЙ ФУНКЦИИ
1. Если дробь неправильная, надо выделить целую часть рациональной дроби,
разделив числитель на знаменатель по правилу деления многочлена на многочлен.
2. Знаменатель Qn(x) разложим на простейшие сомножители:
Qn(x) = (x – a)k…(x – b)r (x2 + p x + q)l… (x2 + p x + q)s , где многочлены (x2 + p x + q)
не имеют действительных корней.
3. Представим дробь Pm(x) /Qn(x) в виде суммы простейших дробей с
неопределенными коэффициентами:
Pm ( x)
A
A2
Ak
C1 x D1
C2 x D2
Cs x Ds
1
...
...
...
Qn ( x) x a ( x a)2
( x a) k
( x 2 px q) ( x 2 px q)2
( x 2 px q) s
где A1, A2, … ,Cs, Ds неопределенные коэффициенты, которые надо найти.
4. Приведем все дроби в разложении к общему знаменателю и приравняем
числители в обеих частях равенства.
5. Составим систему уравнений, используя равенство многочленов, стоящих в
числителе, приравнивая коэффициенты при одинаковых степенях х.
6. Решим систему уравнений, находя некоторые коэффициенты методом частных
значений, полагая x равным действительным корням знаменателя.
7. Подставим найденные коэффициенты A1, A2, … ,Cs, Ds в разложение дроби.
8. Проинтегрируем простейшие дроби.
25.
ИНТЕГРИРОВАНИЕТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
I. Рассмотрим интегралы вида
1. sin kx cos lxdx
1
sin kx coslx (sin( k l ) x sin( k l ) x)
2
2. cos kx cos lxdx
1
coskx coslx (cos(k l ) x cos(k l ) x)
2
1
sin kx sin lx (cos(k l ) x cos(k l ) x)
2
Можно преобразовать каждое из произведений под знаком
интеграла в алгебраическую сумму и проинтегрировать по
табличным формулам.
3. sin kx sin lxdx
26.
II. Интегралы вида sin m x cos n xdx , где n и m – целые.1. Если n и m – четные, положительные, то применяются формулы
понижения степени:
1 cos2
sin
2
2
2. Если
cos2
1 cos 2
2
2 sin cos sin 2
n или m – нечетное, то непосредственно отделяют от
нечетной степени один множитель.
3. Если n и m – дробные или целые отрицательные и (n + m ) четное
отрицательное, то замена t = tg x, иди t = сtg x.
27.
Пример. Вычислитьsin
3
x cos xdx
2
cos x t
sin xdx dt
sin xdx dt
sin
2
x cos x sin xdx
2
1 cos x cos
2
2
x sin xdx
3
5
t
t
1 t 2 t 2 dt t 2 dt t 4 dt C
3 5
1
1
3
cos x cos 5 x C
3
5
28.
III.R(sin x, cos x)dx
, где R – рациональная функция .
1. Универсальная подстановка:
t tg
x
2dt
x
2
arctg
t
dx
,
2
1 t 2
sin x
2t
1 t2
1 t2
cos x
1 t2
2. Упрощенные подстановки.
a) R( sin x, cos x) R(sin x, cos x)
Подстановка: t cos x
b) R(sin x, cos x) R(sin x, cos x)
Подстановка: t sin x
c) R( sin x, cos x) R(sin x, cos x)
d)
R(ctg x)
R(tg x)
Подстановка: t tg x
Подстановка: t ctg x
29.
ПОДСТАНОВКИ П.Л.ЧЕБЫШЕВАИнтеграл вида
m
n
p
x
(
ax
b
)
dx , где m, n, p – рациональные числа
выражается через элементарные функции только в следующих случаях:
1. p < 0 – целое x = t s, d x = s t s-1 d t , s – нок знаменателей m и n;
t b
2.
m 1
n
3.
m 1
p – целое
n
s
1
n
;
– целое axn b t s , s – знаменатель дроби p= к/s, x
a
x a t b
1
n
s
1
n
.
axn b t s x n , s – знаменатель дроби p= к/s,
30.
«НЕБЕРУШИЕСЯ ИНТЕГРАЛЫ»Интегралы вида R x, Pn ( x) dx , где Pn (x) – многочлен
степени выше второй, в общем случае не выражается через
элементарные функции. При этом если n = 2 или n = 3, то
они называются эллиптическими, п > 4, то ультраэллиптическими.
Интегралы от трансцендентных функций:
e
1.
x2
dx – интеграл Пуассона;
sin x
2.
dx ,
x
3. 1 dx ,
ln x
2
4. sin x dx ,
cos x
x dx – интегральный синус, косинус;
ex
dx
x
2
cos x dx
– интегральный логарифм;
– интегралы Френеля и др.
31. Определенный интеграл
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ32.
Определение. Под определенным интеграломот данной непрерывной функции f(x) на данном
отрезке
[a,b]
понимается
соответствующее
приращение ее первообразной, т.е.
b
f ( x) F (b) F (a)
– формула Ньютона-Лейбница.
a
b
f ( x)dx
Обозначение.
a
a и b - пределы интегрирования, соответственно –
нижний и верхний.
[a,b] –промежуток интегрирования,
f(x) – подынтегральная функция.
33.
Пример. Найти интеграл отРешение.
3
4
x
3
1 x dx 4
x 3 на отрезке [1; 3].
4
3
1 81 1 80
3
20
1
4 4
4
4
34.
СВОЙСТВА ОПРЕДЕЛЕНОГОИНТЕГРАЛА
a
1.
f ( x)dx 0 .
a
b
2.
a
f ( x)dx f ( x)dx .
a
3.
4.
5.
b
b
b
a
a
сf ( x)dx с f ( x)dx .
b
b
b
a
a
a
[ f ( x) g ( x)]dx f ( x)dx g ( x)dx .
Если a < c < b , то
b
c
b
f ( x)dx f ( x)dx f ( x)dx
a
a
6. Если f (x) 0 [a ,b] , a < b, то
.
c
b
f ( x)dx 0
a
.
35.
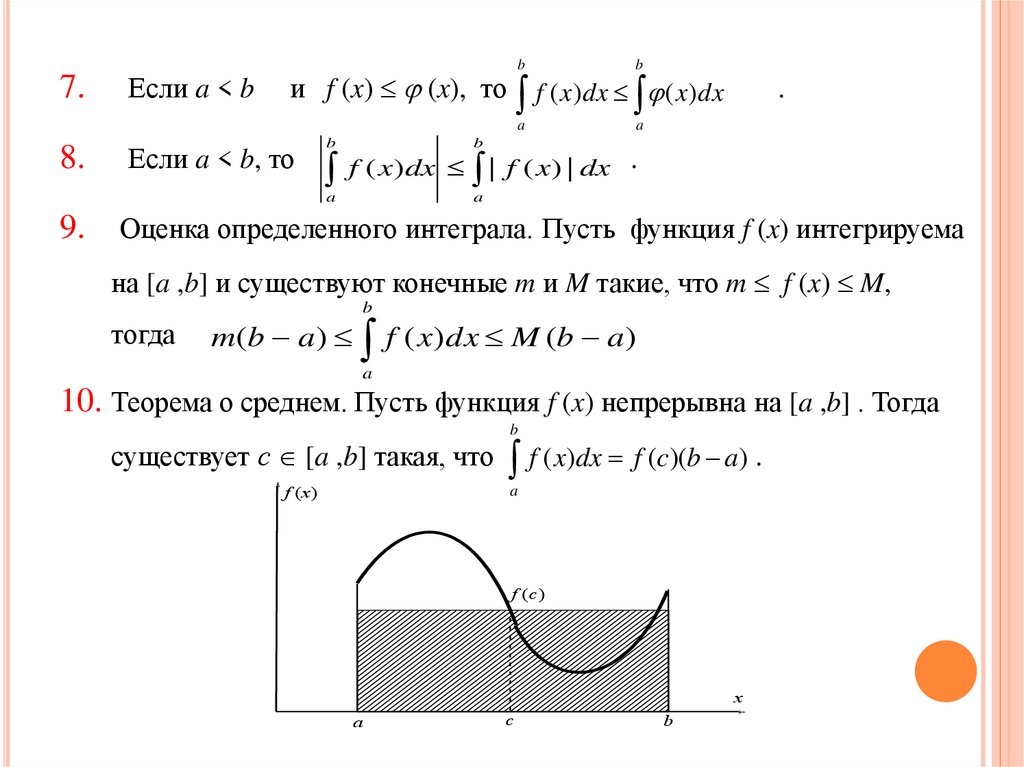
7.Если a < b
b
и f (x) (x), то
f ( x)dx ( x)dx
a
8.
Если a < b, то
b
f ( x)dx
a
9.
b
.
a
b
| f ( x) | dx .
a
Оценка определенного интеграла. Пусть функция f (x) интегрируема
на [a ,b] и существуют конечные m и M такие, что m f (x) M,
b
тогда
m(b a ) f ( x)dx M (b a )
a
10. Теорема о среднем. Пусть функция f (x) непрерывна на [a ,b] . Тогда
существует с [a ,b] такая, что
f (x)
b
f ( x)dx f (c)(b a) .
a
f (c)
x
a
c
b


























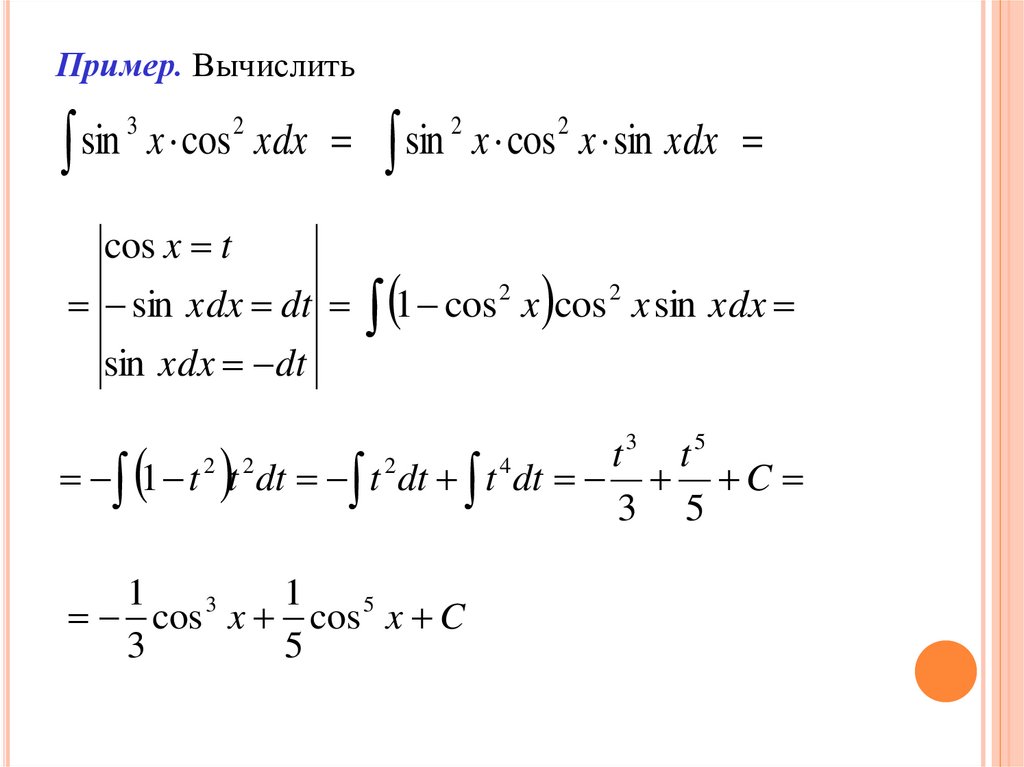







 Математика
Математика








