Похожие презентации:
Комбинаторные задачи
1.
Разработано:Учитель математики
МБОУ СОШ №8
Исакова Марина Викторовна
г. Бердск
2.
– раздел математики, в котором изучают вопросы о том,сколько различных комбинаций, подчинённых тем или
иным условиям можно составить из данных объектов.
3. Как всё начиналось…
Термин «комбинаторика» был введён в математическийобиход Лейбницем, который в 1666 году опубликовал свой
труд «Рассуждения о комбинаторном искусстве».
известный немецкий учёный
Готфрид Вильгельм Лейбниц.
(1.07.1646 - 14.11.1716)
Первоначально комбинаторика возникла в XVI в. в связи с
распространением различных азартных игр.
4.
•учебные заведения•сфера общественного питания
•лингвистика
•география
•спортивные соревнования
•производство
•доставка почты
5.
•агротехника•азартные игры
•химия
•биология
•криптография
•астрология
•экономика
•криптография
6. Способы решения комбинаторных задач
Перебор возможных вариантов.Таблицей.
Дерево возможных вариантов.
Правило умножения.
Правило треугольника.
С помощью графов.
7. Перебор возможных вариантов
Сколько существует двухзначных чисел,составленных из цифр: 0, 5, 8 ?
Решение.
58, 50, 80, 85.
• Ответ: 4 числа.
8. Таблицей
Алла, Бэла, Валентина и Галина во время майскогопраздника подарили друг другу по одному цветку.
Причём каждая девочка подарила каждой по
одному цветку. Сколько всего цветков было
подарено?
Решение.
Ответ: 12 цветков.
А
Б
В
Г
А
-----
+
+
+
Б
В
Г
+
+
+
___
+
+
+
---+
+
+
----
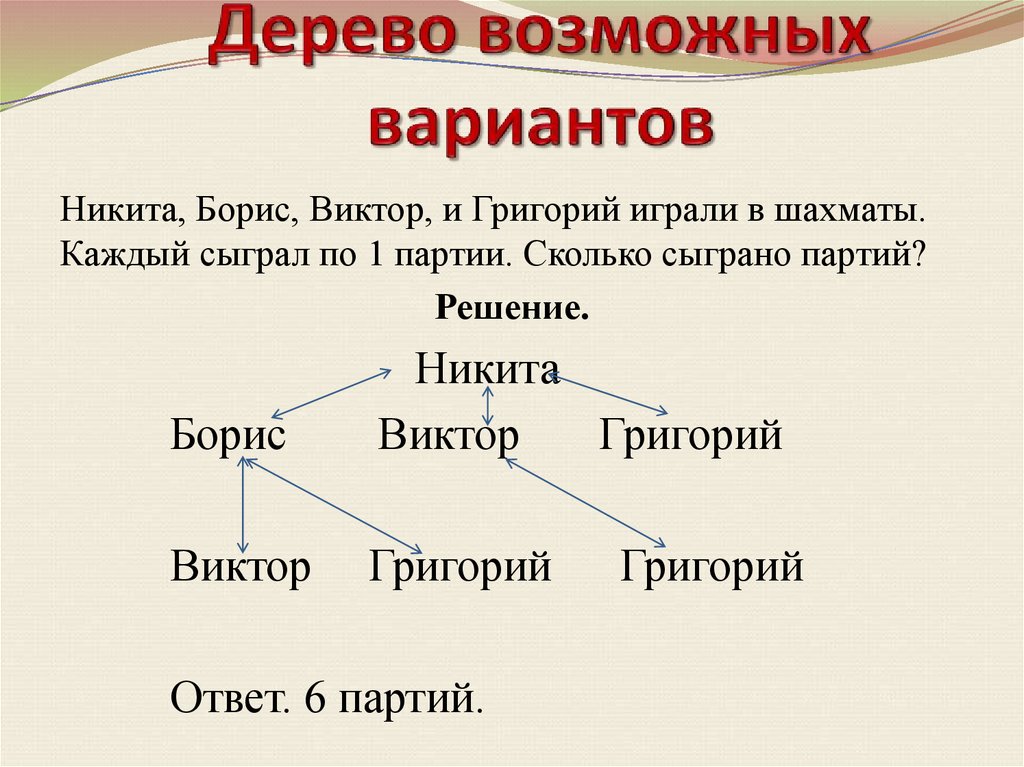
9. Дерево возможных вариантов
Никита, Борис, Виктор, и Григорий играли в шахматы.Каждый сыграл по 1 партии. Сколько сыграно партий?
Решение.
Борис
Никита
Виктор
Григорий
Виктор
Григорий
Ответ. 6 партий.
Григорий
10. Правило умножения
В меню в столовой предложены на выбор 3 первых блюда,5 вторых и 4 третьих блюд. Сколько различных вариантов
обедов, состоящих из 1 первого, 1 второго и 1 третьего
блюда, можно составить из предложенного меню?
• Решение.
• 3*5*4=60
• Ответ: 60 блюд.
Для того, чтобы найти число всех возможных
комбинаций, состоящих из двух составляющих
событий A и B,
следует перемножить число всех возможных вариантов
выбора события A на количество возможных вариантов
выбора события B.
А* В
11. Правило треугольника
Встретились 5 приятелей и обменялисьрукопожатиями. Сколько всего сделано
рукопожатий?
• Решение.
1 2 3 4 5
1 - + + + +
2 - - + + +
3 - - - + +
4 - - - - +
5 - - - - Ответ: 10 рукопожатий.
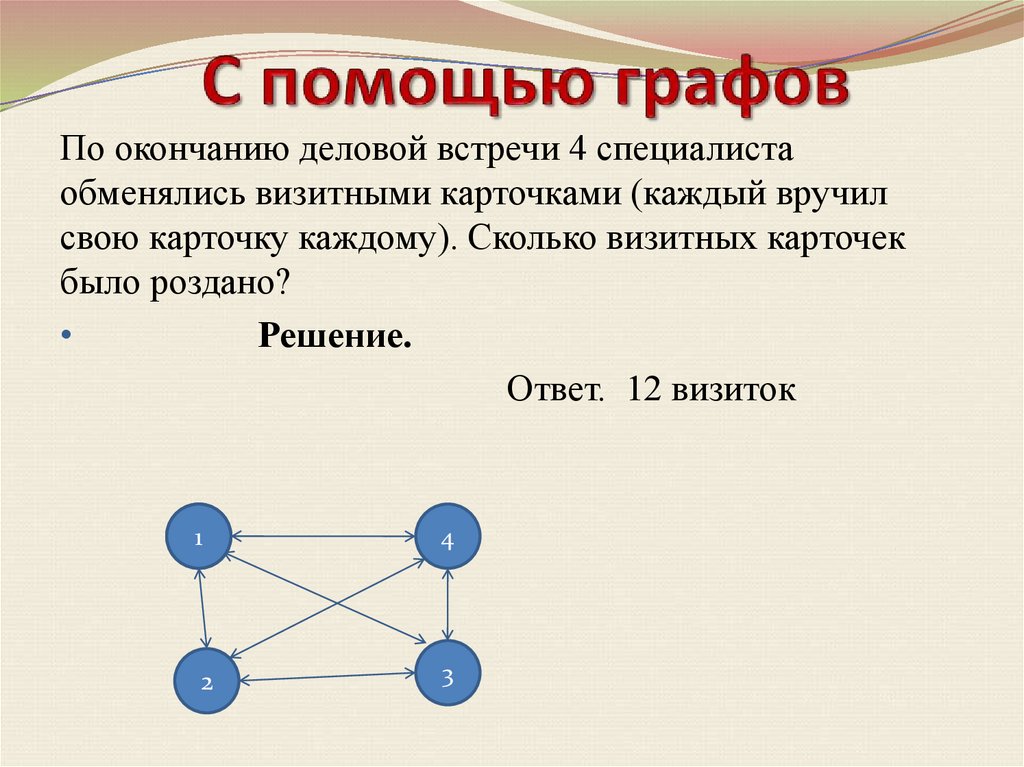
12. С помощью графов
По окончанию деловой встречи 4 специалистаобменялись визитными карточками (каждый вручил
свою карточку каждому). Сколько визитных карточек
было роздано?
Решение.
Ответ. 12 визиток
1
4
2
3
13. Решите задачу несколькими способами
Андрей, Борис, Виктор и Григорий послевозвращения из спортивного лагеря подарили друг
другу на память свои фотографии. Причём каждый
мальчик подарил каждому по 1 фотографии.
Сколько всего фотографий было подарено?
14.
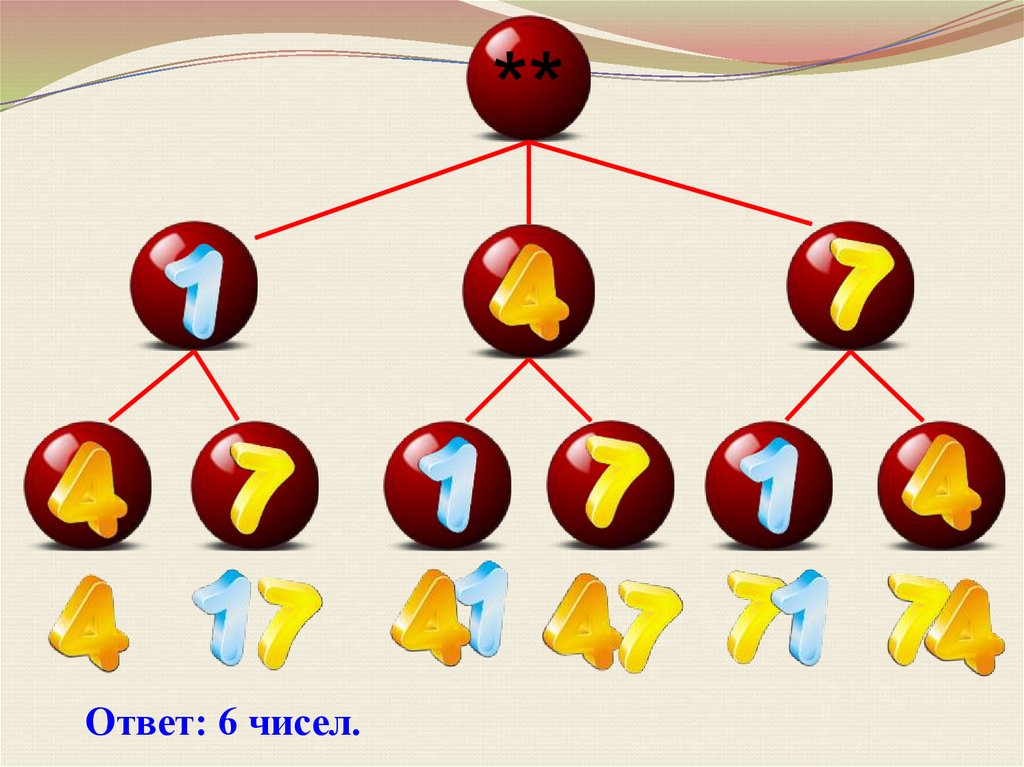
Задача 1Сколько двузначных чисел можно составить из цифр 1,4,7,
используя в записи числа каждую из них не более одного
раза?
Решение:
1 способ: перебор вариантов.
Для того, чтобы не пропустить и не повторить ни одно из
чисел, будем записывать их в порядке возрастания. Сначала
запишем числа, начинающиеся с цифры 1, затем с цифры 4, и,
наконец, с цифры 7:
14, 17, 41, 47, 71, 74.
Ответ: 6 чисел.
15.
**Ответ: 6 чисел.
16. Задача 2.
Правило суммы.Сколько существует способов выбрать кратное двум или
трем число из множества чисел : 2,3,4,15,16,20,21, 75,28 ?
Решение: К1=5 –кратное 2 (2,4,16,20,28),
К2=4 – кратное 3 (3,15,21,75)
К1+К2 = 5+4 = 9
17. Задача 3
Правило произведенияа) Сколько различных двузначных чисел
можно составить из цифр 1, 3, 5, 7, 9?
б) Сколько среди них чисел, кратных 5?
Решение:
а) N= 5х5 = 25 ( Если не сказано, что элемент не повторяется, то
выборка с повторениями)
б) Число кратно 5, если оканчивается цифрой 5 или 0. В нашем
случае – 5.
На первой позиции фиксируем одну из пяти цифр, на второй –
5.
N= 5х1 =5
18. Задача 4
Несколько стран в качестве символа своего государстварешили использовать флаг в виде четырех
горизонтальных полос, одинаковых по ширине, но
разных по цвету: белый, синий, красный, зеленый.
У каждой страны свой, отличный от других, флаг.
а)Сколько всего стран могут использовать такую
символику?
Решение: Цвет верхней полосы можно выбрать одним из
4 способов, второй полосы – одним из трех оставшихся,
цвет 3 полосы – одним из 2 оставшихся, а 4 – одним
способом. По правилу произведения N=4х3х2х1=24
19.
б) Сколько всего стран могут использовать такуюсимволику с нижней белой полосой?
Решение: Если фиксировать цвет нижней
полосы, то цвета трех расположенных над ней
полос можно выбрать 3х2х1 = 6 способами
г) Сколько стран могут использовать такую
символику с верхней белой полосой?
Решение: Если фиксировать цвет белой
полосы, то цвета следующих полос можно
выбрать 3х2х1 = 6 способами.
20. Задача 5
На входной двери дома установлен домофон, на которомнанесены цифры 0,1,2,…9.Каждая квартира получает
кодовый замок из двух цифр типа 0-2, 3-7 и т.п. Хватит ли
кодовых замков для всех квартир, если в доме 96 квартир?
(код 0-0 не существует)
Решение: Выбор 1-й цифры – 10 вариантов, 2-й –10
вариантов.
Всего 10х10 – 1 = 99 вариантов
Ответ: хватит.
21.
Задача 6Сколько двузначных чисел, кратных 3, можно
получить из цифр 1, 3, 5, 7, 9?
а) цифры не повторяются
1
3
5
6 вариантов (15,39,57,51,75,93)
7
9
1
11
13
15
17
19
б) цифры могут повторяться
3
31
33
35
37
39
2 варианта (еще 33,99)
5
51
53
55
57
59
7
71
73
75
77
79
9
91
93
95
97
99
Итого: 8 вариантов

















 Математика
Математика








