Окружность и её элементы

1.

ТЕМА:
”ОКРУЖНОСТЬ”.

2.

Окружность.
Радиус.
Хорда.
Диаметр.
Центральный угол.
Центральный угол.
Вписанный угол.
Задача.
Свойство вписанного угла.
Задача.
Теорема о полусумме дуг.
Задача.
Теорема о полуразности дуг.
Задача.
Произведение отрезков пересекающихся хорд.
Пропорциональность отрезков хорд и секущей.
Свойство отрезков касательной.
Задача.
Геометрическое место точек.
Теорема о геометрическом месте точек.
Серединный перпендикуляр.
Описанная окружность. Треугольник, вписанный в окружность.
Задача.
Задача.
Касательная к окружности.
Окружность, вписанная в треугольник.
Задача.
Окружность, описанная около четырехугольника.
Задача.
Окружность, вписанная в четырехугольник.
Задача.

3.

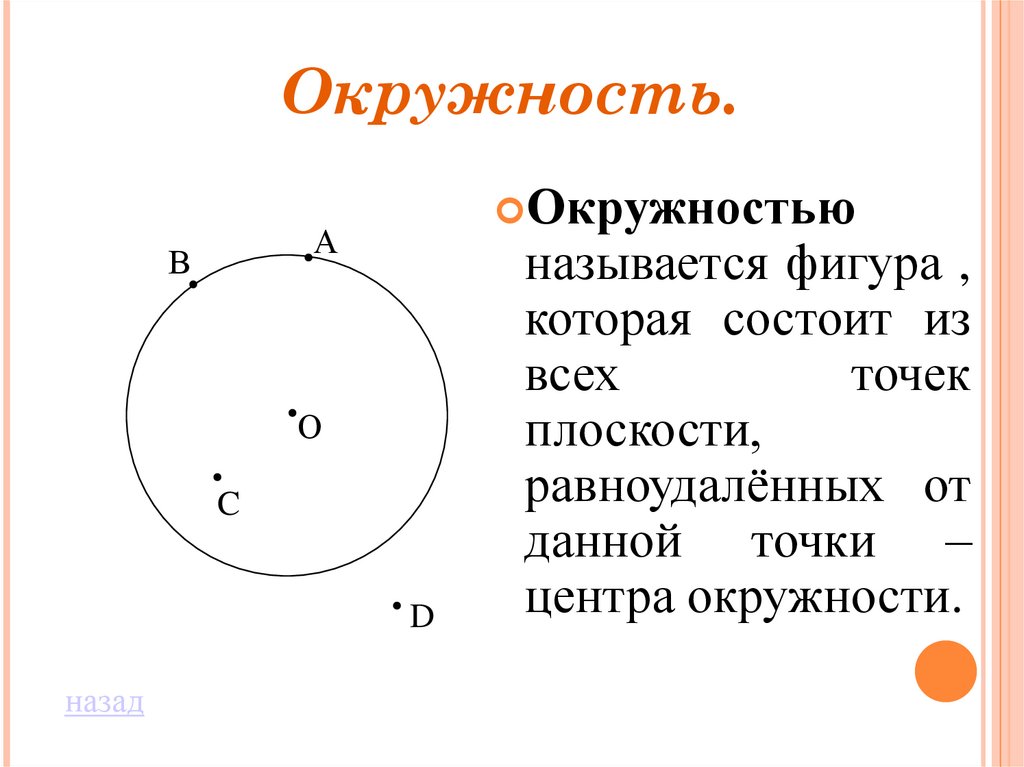
Окружность.
Окружностью
А
В
О
C
D
назад
называется фигура ,
которая состоит из
всех
точек
плоскости,
равноудалённых от
данной точки –
центра окружности.

4.

РАДИУС.
Y
X
Z
назад
Радиусом
называется
отрезок,
соединяющий
центр с любой
точкой
окружности.

5.

ХОРДА.
В
А
О
назад
Хордой
называется
отрезок,
соединяющий две
точки
окружности.

6.

ДИАМЕТР.
А
Диаметром
О
В
назад
называется хорда,
проходящая через
центр.

7.

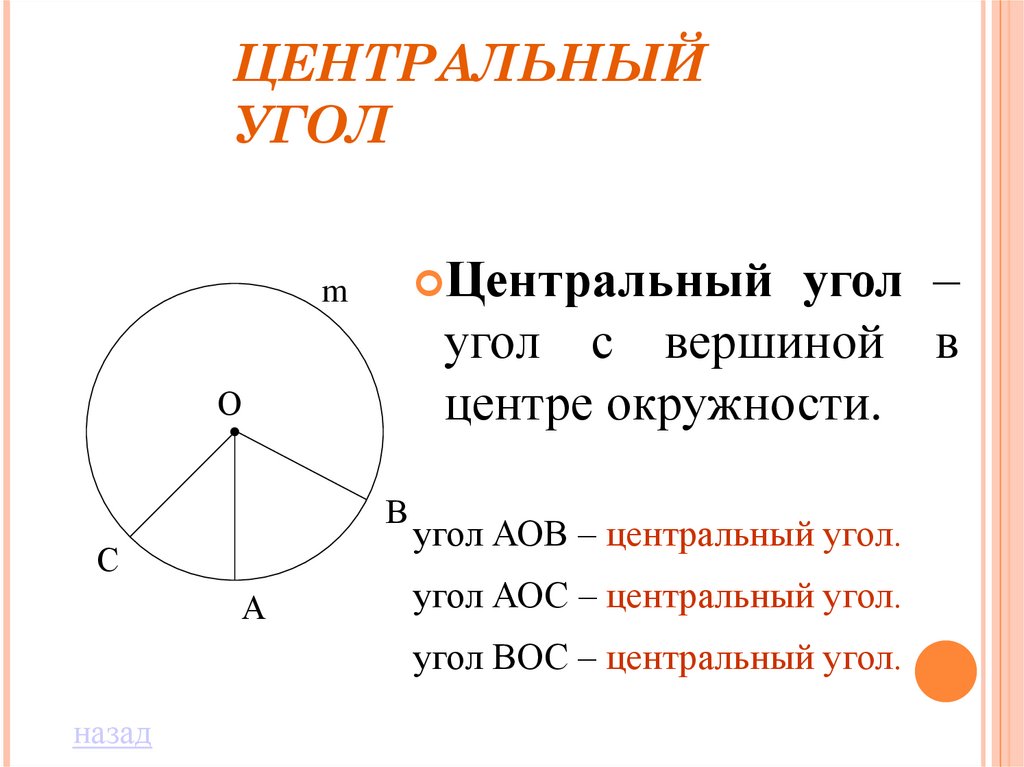
ЦЕНТРАЛЬНЫЙ
УГОЛ
Центральный
угол –
угол с вершиной в
центре окружности.
m
О
В
С
А
угол АОВ – центральный угол.
угол АОС – центральный угол.
угол ВОС – центральный угол.
назад

8.

ЦЕНТРАЛЬНЫЙ
УГОЛ
m
Градусная мера центрального
О
В
С
А
назад
угла соответствует градусной
мере дуги, на которую он
опирается (если дуга меньше
полуокружности).

9.

Если
D
О
С
А
назад
В
центральные
углы
данной
окружности равны, то
соответствующие им
дуги попарно равны.

10.

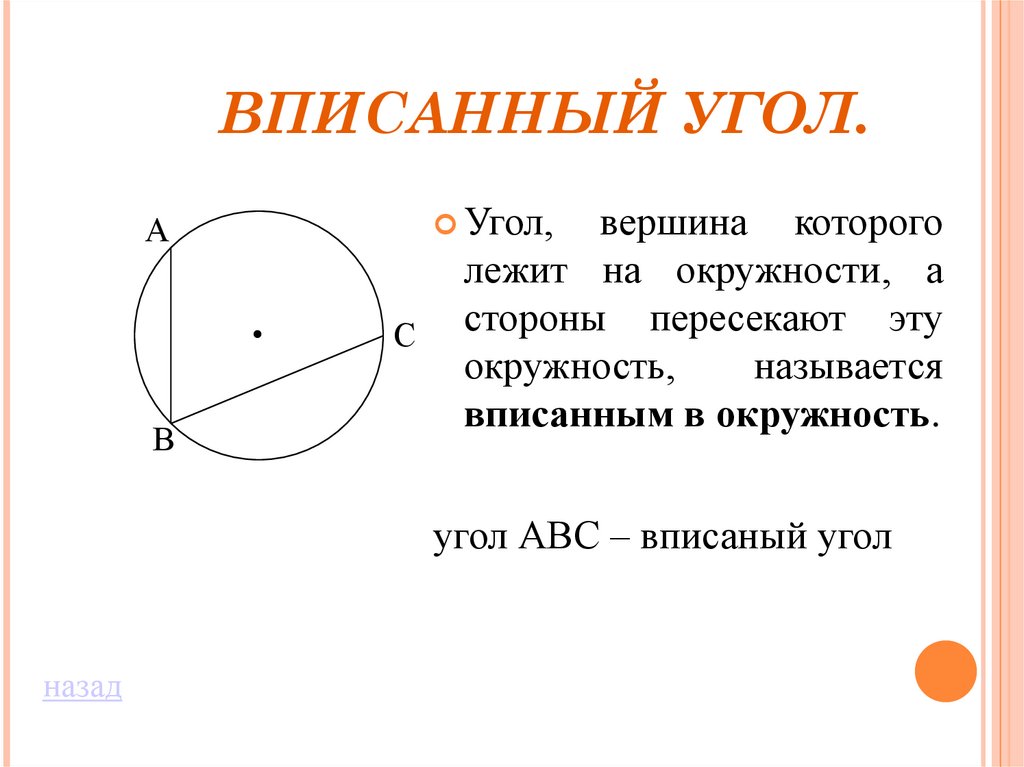
ВПИСАННЫЙ УГОЛ.
Угол,
А
С
В
вершина которого
лежит на окружности, а
стороны пересекают эту
окружность,
называется
вписанным в окружность.
угол АВС – вписаный угол
назад

11.

Углы, связанные с окружностью.
С
о
А
В
Угол АОВ – центральный.
Он равен дуге, на которую
он опирается.
А
В
Угол АСВ – вписанный.
Он равен половине дуги,
на которую он опирается.