Похожие презентации:
Дискретизация сигналов. Теорема отсчётов
1. Дискретизация сигналов. Теорема отсчётов
Кафедра «КРЭМС»Дискретизация
сигналов.
Теорема отсчётов
Зырянов
Юрий Трифонович
доктор технических наук
профессор
2. Сигналы с ограниченной полосой
X ( f ) 0 при fx L2 ( , )
x(t ) 0 при t
Если спектральная плотность финитна
Fв , Fв
x(t)
t
2
3. Теорема отсчётов
Х. Найквист - 1928Э. Уиттекер - 1915
В.А. Котельников - 1933
К. Шеннон - 1948
3
4.
Котельников В.А.”О пропускной способности
«эфира» и проволоки в
электросвязи”.
В сб. Всесоюзный
энергетический комитет.
Материалы к I Всесоюзному
съезду по вопросам
технической реконструкции
дела связи и развития
слаботочной
промышленности. По
радиосекции. – М.:
Управление связи РККА, 1933.
- С. 1-19.
1908 — 2005
4
5. Теорема отсчётов
X(f )Э. Уиттекер - 1915
Х. Найквист - 1928
В.А. Котельников - 1933
К. Шеннон - 1948
Fв
Fв
f
Представим комплексным рядом Фурье
X ( f ) Ck e
k
j
2
kf
2 Fв
,
Fв
1
Ck
X ( f )e
2 Fв F
в
j
2
kf
2 Fв
df , k ,
5
6. Теорема отсчетов Котельникова
Выразим сигналFв
x(t ) X ( f )e
j 2 ft
df
Fв
1
sin 2 Fв t k
2 Fв
Ck 2 Fв
1
k
2 Fв t k
2 Fв
6
7.
Коэффициенты ряда Фурье2
Fв
j
kf
1
2 Fв
Ck
X ( f )e
df
2 Fв F
в
1
x k
2 Fв
2 Fв
7
8.
1d
2 Fв
Обозначим T
sin t kTd
Td
x(t ) x kTd
k
t kTd
Td
sin
t
nT
d
Td
x nTd
n
t nTd
Td
8
9. Теорема отсчётов Котельникова
sint
nT
d
Td
x(t ) x nTd
n
t nTd
Td
Итак
базисные функции
1
Td
2 Fв
n (t ), n ,
0 (t ) sin t
Td
t
Td
n (t ) 0 (t nTd )
9
10.
sint
nT
d
Td
x(t ) x nTd
n
t nTd
Td
10
11. Базис Котельникова
СравнимX ( f ) Ck e
2
j
kf
2 Fв
k
1
sin 2 Fв t k
2 Fв
x(t ) Ck 2 Fв
1
k
2 Fв t k
2 Fв
11
12.
согласно обобщённой формуле Рэлея1
1
sin 2 Fв t k
sin 2 Fв t m
2 Fв
2 Fв
,
1
1
2 Fв t m
2 Fв t k
2 Fв
2 Fв
1 j 2 kf 1 j 2 mf
2 Fв
2 Fв
e
,
e
2 Fв
2 Fв
12
13.
1 j 2 kf 1 j 2 mf2 Fв
2 Fв
e
,
e
2 Fв
2 Fв
Fв
1
e
2
4 Fв F
2
j
( k m) f
2 Fв
в
Fв
1
( k , m )
e
2
4 Fв F
в
1
km
df
2 Fв
2
j
( k m) f
2 Fв
1
df
km
2 Fв
Базис ортогональный ненормированный
13
14. Восстановление аналогового сигнала по отсчётам
0 (t ) sin t tTd Td
(t )
ЛИС-цепь
(t nTd )
x(nTd ) (t nTd )
sin t nTd
Td
n (t )
t nTd
Td
sin t nTd
Td
x(nTd )
t nTd
Td
14
15.
Осталось просуммировать по nv(t ) x(nTd ) (t nTd )
n
ЛИС-цепь
sin
t
nT
d
Td
x(t ) x nTd
n
t nTd
Td
15
16.
Спектральная трактовкаВоздействие (иАИМ-сигнал)
v(t ) x(nTd ) (t nTd )
n
x(t ) (t nTd ) x(t ) (t )
n
где (t )
(t nTd )
n
0
ЛИС-цепь
16
17.
Согласно теореме умноженияV ( f ) X ( f ) ( f )
v(t ) x(t ) (t )
(t ) Sn e
n
2
j nt
Td
ряд Фурье с коэффициентами
Td /2
1
Sn
(t )e
Td T /2
2
j nt
Td
d
1
dt
Td
Поэтому спектральная плотность
1
n
( f )
f
Td n
Td
17
18.
Спектральная плотность( f )
Fd
V ( f ) X ( ) ( f )d
1
n
X ( )
f d
T
T
d
d
n
18
19.
1n
X ( ) f d
Td n
Td
1
n
X(f )
Td n
Td
1
X ( f nFd )
Td n
0
Fd
19
20.
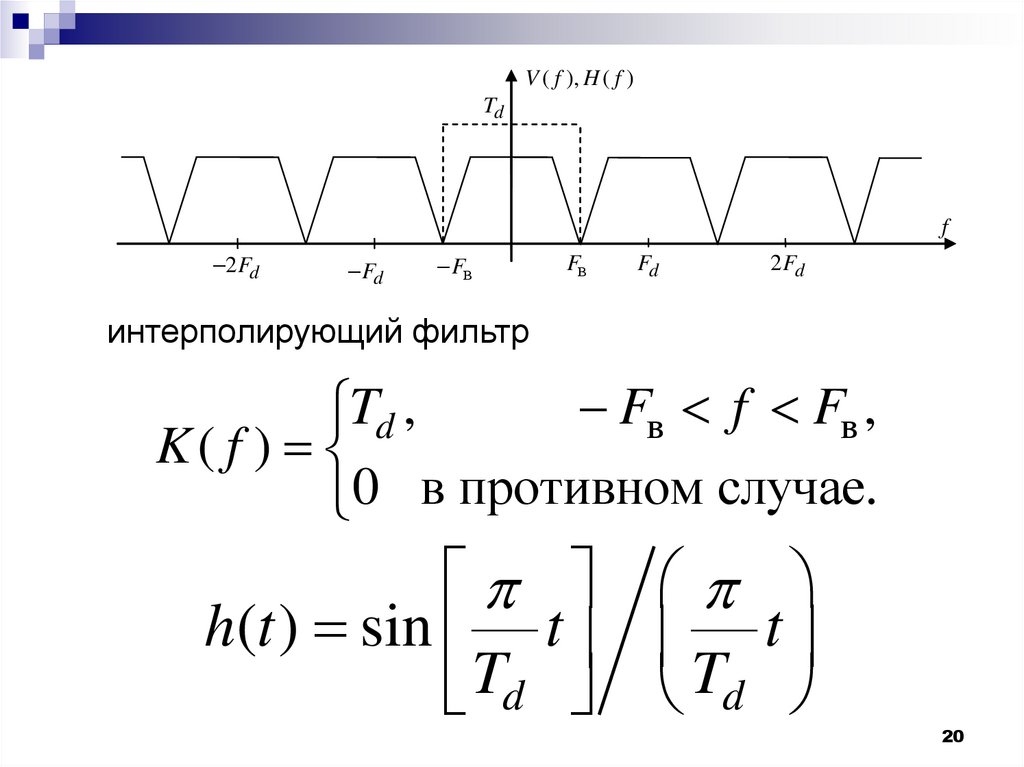
V ( f ), H ( f )Td
f
2 Fd
Fd
Fв
Fв
Fd
2 Fd
интерполирующий фильтр
Fв f Fв ,
Td ,
K( f )
0 в противном случае.
h(t ) sin t
Td
t
Td
20
21. Что мешает точному осуществлению условий теоремы отсчётов на практике?
1. Все сигналы имеют конечную длинунефинитную спектральную плотность
2. Интерполирующий фильтр с прямоугольной
КЧХ физически неосуществим (некаузален)
3. Периодическая последовательность дельтафункций неосуществима
0 (t )
0
hˆ(t )
t
21
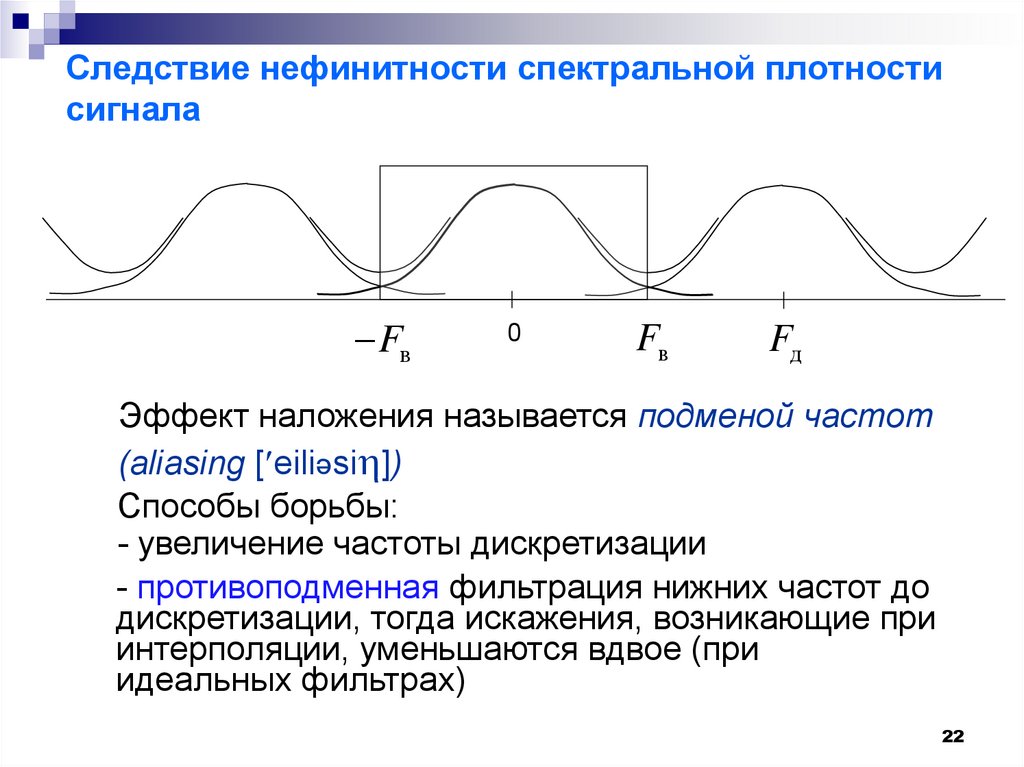
22. Следствие нефинитности спектральной плотности сигнала
Fв0
Fв
Fд
Эффект наложения называется подменой частот
(aliasing [ eiliəsi ])
Способы борьбы:
- увеличение частоты дискретизации
- противоподменная фильтрация нижних частот до
дискретизации, тогда искажения, возникающие при
интерполяции, уменьшаются вдвое (при
идеальных фильтрах)
22
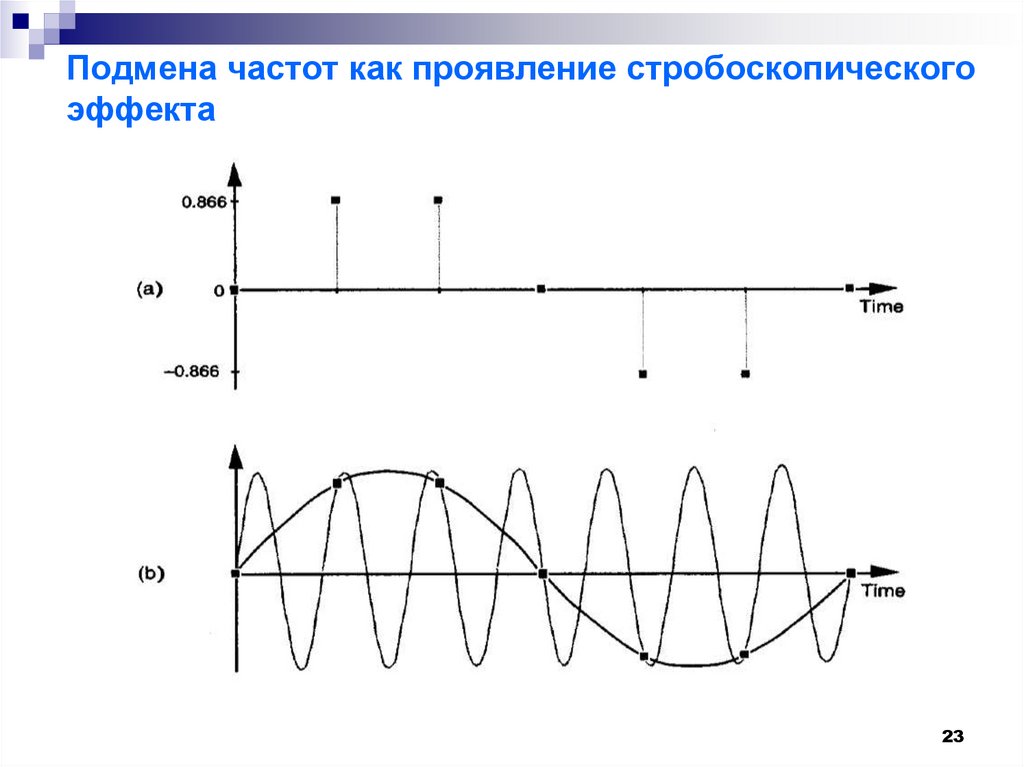
23. Подмена частот как проявление стробоскопического эффекта
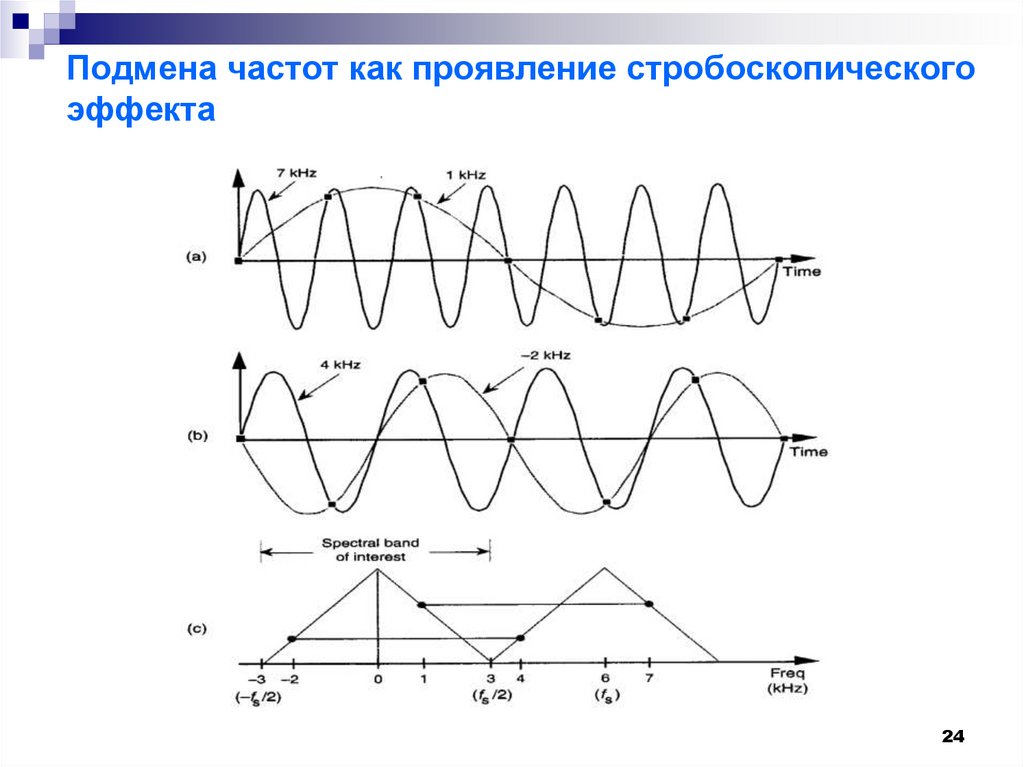
2324. Подмена частот как проявление стробоскопического эффекта
2425. Различие дискретизации и интерполяции
v(t ) x(t ) (t )описывает процесс интерполяции
(восстановления аналогового
сигнала по его отсчетам)
Взятие (одиночного) отсчёта аналогового сигнала
(стробирование) описывается выражением типа
свёртки
x(t0 ) x(t ) (t t0 )dt x(t ) (t0 t )dt
x(t0 ) x(t )d (t0 t )dt
импульс должен быть значительно
короче АКФ сигнала (форма тогда
не имеет значения)
25





















 Электроника
Электроника








