Самостоятельные и контрольные работы для 7 класса по алгебре и геометрии

1. Самостоятельные и контрольные работы для 7 класса по алгебре и геометрии

2.

Алгебра
Геометрия

3.

Самостоятельные работы
Контрольные работы

4.

Самостоятельные работы
Контрольные работы

5. Темы:

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
Числовые выражения.
Свойства действий над числами.
Линейное уравнение с одной переменной.
Вычисление значений функции по формуле.
Линейная функция и ее график.
Взаимное расположение графиков линейных функций.
Определение степени с натуральным показателем.
Умножение и деление степеней. Возведение в степень
произведения и степени.
Умножение одночленов.
Возведение одночлена в степень.
Сложение и вычитание многочленов.
Умножение одночлена на многочлен.

6. Темы:

13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
Разложение многочлена на множители способом
группировки.
Квадрат суммы и квадрат разности.
Разность квадратов.
Преобразование целого выражения в многочлен.
Применение различных способов для разложения на
множители.
Линейные уравнения с двумя переменными.
График линейного уравнения с двумя переменными.
Графический способ решения систем уравнений.
Способ подстановки.
Способ сложения.
Решение задач с помощью систем уравнений.

7.

Контрольная
Контрольная
Контрольная
Контрольная
Контрольная
Контрольная
Контрольная
Контрольная
Контрольная
Контрольная
работа
работа
работа
работа
работа
работа
работа
работа
работа
работа
№1.
№2.
№3.
№4.
№5.
№6.
№7.
№8.
№9.
№10 (Итоговая).

8.

1.Найдите значение выражения:
2
1
1
а) (10 5 ) : 3 ;
б) (3,38 2,24) : 1,25
3
3
3
в) 0,7 1,3 5,1 : 0,17
2. Вычислите сумму квадратов чисел
-3,1 и 2,9.
3. Какой цифрой оканчивается разность:
а) 114
2
7 ;
3
б)
115 15 .
3
2

9.

1.Вычислите наиболее рациональным способом
а) 6,83 7,81 3,17 8,19 ;
7
2 31
13
б) ( 31) ( 13 ) 7 ( 20 )
в) 2 13,5 19 ;
19
1
7
3
1
г) 7 13 15 17 ;
4
8
4
8
;
д)
1 2 3 4 5 6 7
.
2 3 4 5 6 7 8
.
2. Найдите значение выражения, используя
распределительное свойство умножения:
1
5
;
а) (10 ) 13 б) 12 3 ;
13
12
1
в) 9 8 .
4

10.

1. Решить уравнения:
а) 8х 24; б) 3 у (5 у ) 11;
в) (7 х 1) (6 х 3) 5; д) 4( х 2) 4 х 13;
е) 8 х 40 8( х 2) 24;
г)
3
2
х
7
14
.
.
2. При каком t значение выражения 13t-17 на
8 меньше значения выражения 12t+11?
;
3. Среди данных уравнений укажите те,
которые не имеют корней:
5х 10 4х; 3х 7 3х 11; х 8; х 1 0.
;
;
.

11.

1.Найдите значения функции,
заданной формулой:
1) у 4 х 8 для значений аргумента,
равных -3; 0; 1; 6;
2
2) у х для значений аргумента,
равных -4; 0; 3; 4,5.
2. Найдите значения аргумента, при котором
функция у 2,5 х принимает значение,
равное 12.
3. Найдите значение переменной b,
соответствующие значениям переменной
равным -5; 0; 4: b 5 a ; b a 4 .

12.

1.Постройте график линейной функции:
а) у х 1; б) у 5; в) у 4 ;
2
г) у х 2.
3
2. Постройте в одной системе координат
графики функций и укажите координаты
точки их пересечения:
у 0,5 х 1 и у х 4.
.

13.

1.Постройте в одной системе координат график
функций:у 1 х 1 у 1 х 2 у 1 х.
;
;
3
3
3
Ответьте на вопросы:;
а) Чему равен угловой коэффициент каждой прямой?
;
б) Каково взаимное расположение графиков функций
в) Каковы координаты точек пересечения каждого
графика с осями координат?
2. Пересекаются ли графики
функций:
и
у 2 х 4 и у 4 х 2; у 2 х 3 и у 2 х 3
В том случае, когда графики пересекаются,
постройте их. Определите по графику координа
точки пересечения и проверьте результаты
вычислением.
.

14.

1.Найдите значение выражения:
1 5
1
2
3
4
2
(
1
)
;
(
8
)
;
(
)
;
(
0
,
5
)
;
г)
д)
е)
а) 3 ; б) (0,6) ; в) 4
2
3
ж) ( 1) ;
1 4
з) ( 3 ) ;
и)
к) ( 0,1) 4 .
2. Сравните с нулем значение выражения
(ответ запишите в виде неравенства):
5
2
3
2
в)
г)
47
;
8
,
5
.
а) ( 9,2) ; б) ( 13,6) ;
7
3. Вычислите:
3 2
2
а) 0,1 60 ; б) (4 ) ;
8
г)
10 ( 5) ;
4
3
72 ;
3
2
6
(
8
)
;
в)
д) ( 1) ( 1) ; е) (4,9 5,1) .
5
10
5

15.

1.Представьте в виде степени произведение:
8 4
2 3
6 3 7
3
6
9
3
3.
б)
в)
г)
x x x ;
а)bb b ;
( 7) ( 7) ( 7) ;
2. Представьте в виде степени частное
14
8
а) a : a ; б) (0,1) 20 : (0,1) 6 ; в) a 5 : a 5 ; г) ( 0,5)16 : ( 0,5) 8 .
3. Найдите значение выражения:
14
7
( 3) 5 ( 3) 3
10
10
; б)
а)
.
19
7
( 3)
10
4. Возведите в степень произведение:
2
1
4
4
9
7
2
(
abc
)
.
(
a
)
;
(
2
ac
)
;
(
ab
)
;
б)
в)
г)
д)
е)
(
xyz
)
;
( 0,4c) ;
а)
3
3
5. Представьте произведение в виде степени:
5 5
x
а) y ; б) 36a 2 b 2 ; в) 0,001x 3 c 3 ; г) 1 x a b .
16
6. Выполните возведение в степень:
а) ( х 5 ) 2 ; б) ( х10 )10 ; в) ( х m ) 2 ; г) ( х 3 ) 2 .
3
4
4
4

16.

1.Выполните умножение:
2
а) a12ab 2 ; б) 0,5x 2 y( xy);
3
в) 0,4 x 4 y 2 2,5x 2 y 4 .
2. Замените * таким одночленом станда
ного вида, чтобы выполнялось равенств
а) 6a 2 24a 3b; б) 5x 2 y 3 30 x 3 y 5 .
3. Найдите значение выражения:
а)
516 316
;
14
15
б)
27 2 9 4
;
2
81
в) 5 20 : (5 2 ) 5 : 58.

17.

1.Выполните возведение одночлена в степ
1
2
а) (8х) ; б) ( 3 а ) ; в) (0,2 у ) ; г) (4 ху) ;
2 3
д) ( 10а b
3
3
3 4
2 4
) .
2. Преобразуйте выражение в одночлен
стандартного вида:
3 2
6
5
3 4
3
2
(
с
)
12
с
;
0
,
4
х
(
2
х
)
;
а) 20а (5а) ; б)
в)
г) (4ас 2 ) 3 (0,5а 3 с) 2 ;
д) ( 2 х 2 у 3 )3 ( 9 х 4 ) 2 .
3

18.

1.Составьте сумму и разность многочленов
и приведите к стандартному виду:
а) 2 у 2 8 у 11 и 3 у 2 6 у 3;
б) 4m 4 4m 2 13 и 4m4 4m2 13;
2. Упростите выражение:
а) (2a 5b) (8a 11b) (9b 5a);
б) (3x 10 y) (6 x 3 y) (6 y 8x);
в) (8c 3c) ( 7c 11c 3) ( 3c 4);
г) (a b c) (a b) (a b c).
3. Докажите, что значение выражения
2
2
2
(a 2 6ab 9b 2 ) (3a 2 ab 7b 2 ) (a 2 5ab 2b 2 )
не зависит отb.

19.

1.Решите уравнение:
а) (3х 5) (8 х 1) 17;
б) 6 х 5(3х 2) 5( х 1) 8;
в)
х х 2 1
;
5
15
3
8 х 3 3х 1
2.
7
10
г)
2. Решите задачу:
Мастер изготовляет на 8 деталей в час
больше, чем ученик. Ученик работал 6 ч,
а мастер 8 ч, и вместе они изготовили 23
детали. Сколько деталей в час изготовля
ученик?

20.

1.Вынесите за скобки общий множитель:
а) a( x 2) ( x 2); б) (c 8) c(c 8);
в) x(a 5) (5 a); г) m n (n m) y.
2. Разложите многочлен на множители:
2
2
a
b
2
a
ab;
px
py
5
x
5
y
;
в)
а)
2
г)
2
x
3x 4ax 6a.
б) ab ac 4b 4c;
3. Разложите на множители:
2
а) x 3x 2;
б)
x 2 5 x 6.

21.

1.Представьте в виде многочлена:
а) ( x 7) 2 ; б) (5а 1) 2 ; в) (10 4с) 2 ;
2
2
г) ( 3с а) ; е) ( 5а 8b) ; д) (а 2 6) 2 .
2. Представьте многочлен в виде квадрат
двучлена:
2
2
4
a
4
ab
b
;
а)
2
2
9
a
6
ab
b
;
б)
в)
г)
9 2
16 2
a 2ab b ;
16
9
1 2
a ab b 2 ;
4
д)
a 2 b 2 2ab 1;
е)
b 2 2a 2 b a 4 .

22.

1.Разложите на множители:
2
2
2
2
2
2
n
b
;
а) 4 х 1; б) 1 9а ; в) m a ; г)
2
2
2
2
;
81
х
y
a
16
y
;
д)
е)
ж) 49 х 2 121a 2 ;
з)
100a 25b ;
2
2
и) c a b .
2
2 2
2. Представьте в виде произведения:
2 2
а) 25 36 p c ; б) (3 х) 2 4; в) (3х 1)2 (4x 3)2 .
3. Разложите на множители:
а) х 2 n 9; б) b 2 a 4 n ; в) х 2n y 2n ; г)
81a 8 n 16.

23.

1.Упростите выражение:
а) (4a b)(a 6b) a(25b 3a);
б) (3a b)(a 2b) (2a b)(a 5b).
2. Преобразуйте в многочлен:
2
а)3x(3x 7) (3x 1) ;
б) ( p 1) 2 ( p 2) 2 .
3. Найдите значение выражения:
(7 x)(7 x) ( x 3) 2
при
x 3,5.

24.

1.Разложите на множители:
2
2
2
2
а) 3х 12; б) bх 9b; в) 2 p 98a ;
г) 3a 3ab .
2
2
2. Представьте в виде произведения:
2
2
а) 3a 6ab 3b ;
б) a 2 b abc bc 2 ;
в) 2 x 2 4 x 2;
г) 5a 10ab 5b ;
д) a 2 12ab 36b 2 ;
е) 12 x 3 12 x 2 3x.
2
2

25.

1.Является ли решением уравнения
2
х ху 6 пара чисел:
а) х 3, у 1; б) х 5, у 2;
в) х 6, у 5 ?
2. Найдите три решения уравнения
5 х 2 у 1.

26.

1. Постройте график линейного уравнени
4 х 3 у 6.
2. Известно, что график уравнения
х 2у 2
проходит через точку А, абсцисса
которой равна 2. Найдите ординату
этой точки.

27.

Решите с помощью графиков
систему уравнений:
у х,
а)
у 2 х;
х у 0,
б)
х 2 у 2;
2 х у 1,
в)
х у 2.

28.

1. Выразите в следующих уравнениях
х
через у и у через х:
а)х 3 у 6; б) 2 х у 3;
в) х 5 у 0.
2. Решите систему уравнений способом
подстановки:
х у 5,
а)
3х у 7;
3m 2n 5,
б)
m 2n 15.

29.

1. Решите способом сложения систему
уравнений:
2 х 3 у 1,
u v 4,
х у 5,
в)
а)
б)
3
х
5
у
2
.
3
u
5
v
20
;
х
у
7
;
2. Пара чисел (-2; 3) является решением
системы уравнений
3х bу 4b 1,
aх 2 у a b 19.
Найдите значения a и b.

30.

1.В магазине продаются тетради по 96 листов
и по 24 листа. Во всех тетрадях, купленных
Сашей, 528 листов. Сколько толстых и сколько
тонких тетрадей купил Саша, если купленные
им толстые тетради содержат на 48 листов
больше, чем все тонкие?
2. Поезд прошел первый перегон за 2 ч,
а второй за 3ч. Всего за это время он прошел
расстояние 330 км. Найдите скорость поезда
на каждом перегоне, если на втором перегоне
она была на 10 км/ч больше, чем на первом.

31.

1. Сравните значения выражений:
0,8 х 1 и 0,8 х 1 при х 6.
2. Найдите значение выражения:
6 х 8 у при х 2 , у 5 .
3
8
3. Упростите выражение:
а) 2 х 3 у 11х 8 у;
б) 5(2а 1) 3; в) 14 х ( х 1) (2 х 6).
4. Упростите выражение и найдите его
2
значение: 4(2,5а 1,5) 5,5а 8 при а .
9
5. Из двух городов, расстояние между которыми S км,
одновременно на встречу друг другу выехали легковой
автомобиль и грузовик и встретились через t часов. Скорость
легкового автомобиля V км/ч. Найдите скорость грузовика.
Ответьте на вопрос задачи, если S = 200, t = 2,V = 60.
6. Раскройте скобки: 2 р (3 р ( 2 р с)).

32.

1.Решите уравнения:
а)
1
12;
3х
б) 6 х 10,2 0; в) 5х 4,5 3х 2,5;
г) 2 х (6 х 5) 45.
2. Таня в школу сначала едет на автобусе, а потом
идет пешком. Вся дорога у нее занимает 26 мину
Идет она на 6 минут дольше, чем едет на автобу
Сколько минут она едет на автобусе?
3. В двух сараях сложено сено, причем в первом са
сена в 3 раза больше, чем во втором. После того
как из первого сарая увезли 20т сена, а во второ
привезли 10 т, в обоих сараях сена стало поровн
Сколько тонн сена было в двух сараях
первоначально?

33.

1. Функция задана формулой у 6 х 19.Определите:
а) значение у, если х 0,5;
б) значение х, при котором у 1;
в) проходит ли график функции через точку А(-2; 7)?
2. а) Постройте график функции у 2 х 4.
б) Укажите с помощью графика, чему равно
значение у при котором х 1,5.
3. В одной и той же системе координат постройте
графики функций: у 2х; и у 3.
4. Найдите координаты точки пересечения графико
функций: у 47 х 37 и у 13х 23
5. Задайте формулой линейную функцию, график
которой параллелен прямой у 3 х 7
и проходит через начало координат.

34.

1.Найдите значение выражения 1 5 х 2 при
х 4.
2. Выполните действия:
а) у 7 у 12 ; б) у 20 : у 5 ; в) ( у 2 ) 8 ; г) (2 у) 4 .
5 2 3
(
2
a
b ) .
3. Упростите выражение: а) 2ab 3a b ;б)
3
2
4
4. Постройте график функции у x 2 .
С помощью графика функции определите
значение у приx 1,5 и x 1,5.
2
3
2
2
3
4 0
25
5
(
13
12
)
(
6
8
) .
5. Вычислите: а) 7 ; б)
5
6. Упростите выражение:
б) x n 2 x 3 n x.
а) 2 2 x 2 y 8 ( 1 1 xy 3 ) 4 ;
3
2
7. Сережа вычислил степень числа 2 с показателем т – нечет
число. Его брат возвел число, полученное Сережей, в степен
показателем к, где к – четное число. Он получил 1024. Найди
хотя бы одну пару значений т и к, которые могли бы
использовать Сережа и его брат.

35.

1. Выполните действия:
а) (3a 4ax 2) (11a 14ax); б) 3 y 2 ( y 3 1).
2. Вынесите общий множитель за скобки:
3
2
18
a
6
a
.
а) 10ab 15b 2 ;
б)
3. Решите уравнение:
9 x 6( x 1) 5( x 2).
4. Пассажирский поезд за 4 ч прошел такое же
расстояние, какое товарный за 6 ч. Найдите скоро
пассажирского поезда, если известно, что скорость
товарного на 20 км/ч меньше.
5. Решите уравнение:
3х 1 х 5 х
а) 6 3 9 ;
1
б) x 7 x 0.
2
6. Упростите выражение:
2a(a b c) 2b(a b c) 2c(a b c).

36.

1.Выполнить умножение:
а) (с 2)(с 3); б) (2a 1)(3a 4); в) (5 x 2 y)( 4 x y);
.
г) (a 2)(a 2 3a 6).
2. Разложите на множители:
a(a 3) 2(a 3); б) ax ay 5 x 5 y.
а)
.
3. Упростите выражение: 0,1x(2 x 2 6)(5 4 x 2 ).
4. Представьте многочлен в виде произведени
2
.а) x xy 4 x 4 y;
б) ab ac bx cx c b.
5. Из прямоугольного листа фанеры вырезали
квадратную пластинку, для чего с одной сторо
листа фанеры отрезали полосу шириной 2 см,
а с другой 3 см. Найдите сторону получившего
квадрата, если известно, что его площадь на
см 2 меньше площади прямоугольника.

37.

1.Преобразуйте в многочлен:
2
2
(
3
a
c
)
; в) ( y 5)( y 5); г) (4b 5c)( 4b 5c).
б)
а)
. ( 2 x 1) ;
( x y)( x y) ( x 2 3 y 2 ).
.2. Упростите выражение:
3. Разложите на множители:
2
2
2
а)
16
y
0
,
25
;
б)
a
10
ab
25
b
.
.
2
4.
Решите
уравнение
(
5
x
)
x(2,5 x) 0.
.
5. Выполните действия:
2
2
(
2
a
b
)(
2
a
b
); б) ( x 6 x 3 ) 2 ; в) ( y b) 2 ( y b) 2 .
а)
.
6. Решите уравнение:
а) (5x 2)(5x 2) (5x 1) 2 4 x;
б) 100 x 2 16 0.

38.

1.Упростите выражение:
2
б)
(a 7)(a 1) (a 3) ;
а) 2 x( x 3) 3x( x 5);
в) 3( y 5) 2 3 y 2 .
2. Разложите на множители:
2
2
3
а) c 16c; б) 3a 6ab 3b .
3. Упростите выражение:
(3a a ) a (a 2)(a 2) 2a(7 3a ).
2 2
2
2
4. Разложите на множители:
2
2
4
б)
y
x
6 x 9.
а) 81a 1;
5. Докажите, что выражение a 2 4a 9
может принимать лишь отрицательные
значения.

39.

1.Решите систему уравнений: 4 x y 3,
6 x 2 y 1.
2. Студент получил стипендию 100 рублей монетами
достоинством 5 рублей и 2 рубля, всего 32 монеты.
Сколько было выдано студенту пятирублевых и
двухрублевых монет в отдельности?
3. Решите систему уравнений:
2(3x 2 y ) 9 4 x 21,
2 x 10 3 (6 x 5 y ).
проходит через точки А(3; 8) и
4. Прямая y kx b
В(-4; 1). Напишите уравнение этой прямой.
5. Выясните, имеет ли решение система и
сколько?
3x 2 y 7,
6 x 4 y 1.

40.

1 3
x 3 y 2 при
1. Найдите значение выражения
4
x 2 и y 1.
x 2 y 11,
2. Решите систему уравнений
5 x 3 y 3.
3. Разложите на множители: а) 3x 2 30 x 75;
б) 3a 2 3b 2 a b.
4. Пешеход рассчитал, что, двигаясь с определенной
скоростью, намеченный путь он пройдет за 2,5 ч.
Но он шел со скоростью, превышающей намеченную
на 1 км/ч, поэтому прошел путь за 2 ч.
Найдите длину пути.
5. а) Постройте график функцииy 3 2 x.
б) Принадлежит ли графику этой функции
точка М(8; -19)?

41. Темы:

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
Полуплоскости.
Треугольник. Существование треугольника равного
данному.
Смежные углы.
Смежные и вертикальные углы.
Биссектриса угла. Признаки равенства треугольников.
Свойства равнобедренного треугольника.
Свойство медианы равнобедренного треугольника.
Третий признак равенства треугольников.
Сумма углов треугольника.
Сумма углов треугольника. Решение задач.
Окружность.

42. Темы:

1.
2.
3.
4.
5.
№ 1. Основные свойства.
простейших геометрических фигур.
№ 2. Смежные и вертикальные
углы.
№ 3. Признаки равенства
треугольников.
№ 4. Сумма углов треугольника.
№ 5. Геометрические построения.

43.

1. На отрезке АВ взяты точки C и D.
Найдите длину отрезка CD, если
АВ=14 см, АС=3 см, ВD=5 см.
2. На отрезке АВ=27 см отмечена точка К.
Найдите длину отрезков АК и ВК, если
АК больше ВК на 7 см.
3. На прямой отмечены точки А, В, С так,
что АВ=7 м, АС=1 м, ВС=6 м. Какая из
этих точек лежит между двумя другими?

44.

1.Треугольники АВС и FED равны.
Известно, что АВ=7 см, ВС=9см, FD=6 см
Найдите остальные стороны каждого
треугольника.
2. Треугольники АВС и MNR равны.
R
90
, N 60 , А 30 .
Известно, что
Найдите остальные углы каждого
треугольника.

45.

1. Один из смежных углов в 5 раз больше
другого. Найдите величину большего
угла.
2. Могут ли быть смежными прямой и
острый углы? Объясните ответ.

46.

1. Один из смежных углов составляет 1/3
другого. Найдите эти углы.
2. Один из углов, образовавшихся при
пересечении двух прямых, равен 142 .
Найдите остальные углы.

47.

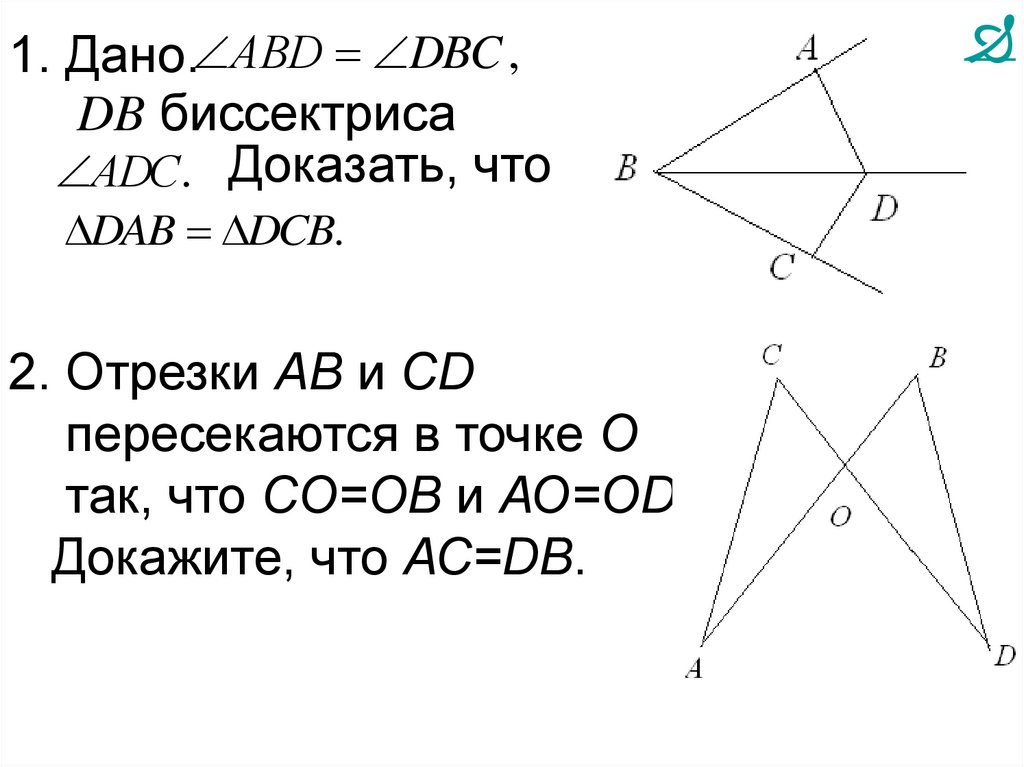
1. Дано. АВD DBC ,
DB биссектриса
АDC. Доказать, что
DAB DCB.
2. Отрезки АВ и CD
пересекаются в точке О
так, что СО=ОB и АО=OD.
Докажите, что АС=DB.

48.

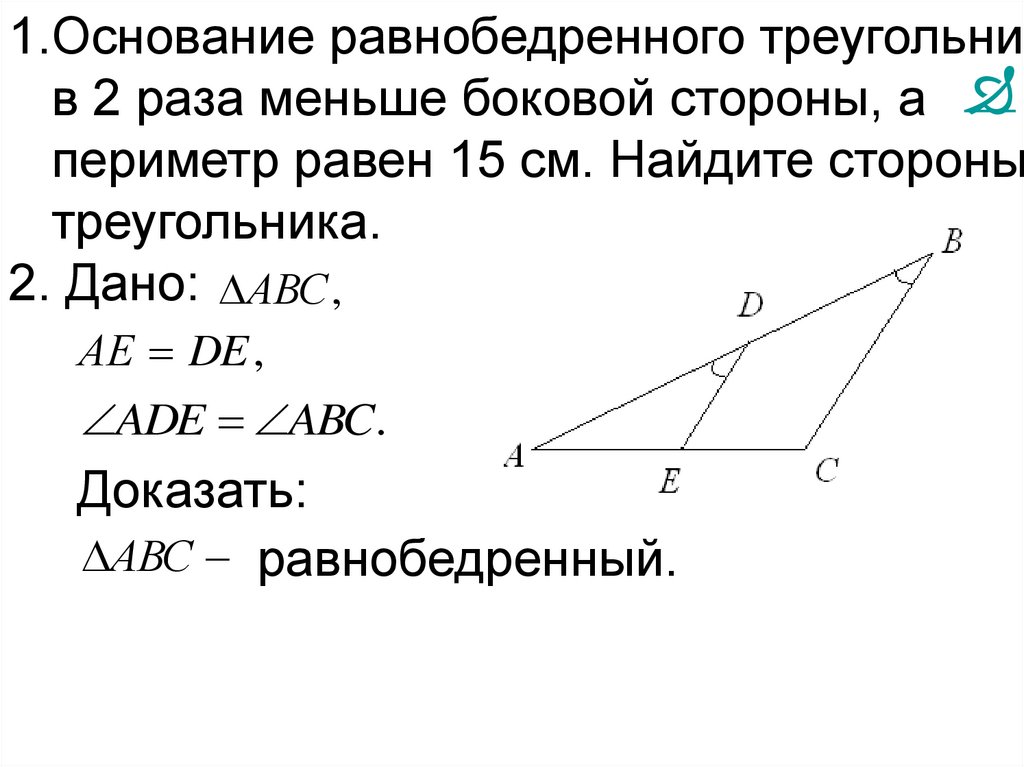
1.Основание равнобедренного треугольник
в 2 раза меньше боковой стороны, а
периметр равен 15 см. Найдите стороны
треугольника.
2. Дано: АВС ,
АЕ DE ,
ADE ABC.
Доказать:
АВС равнобедренный.

49.

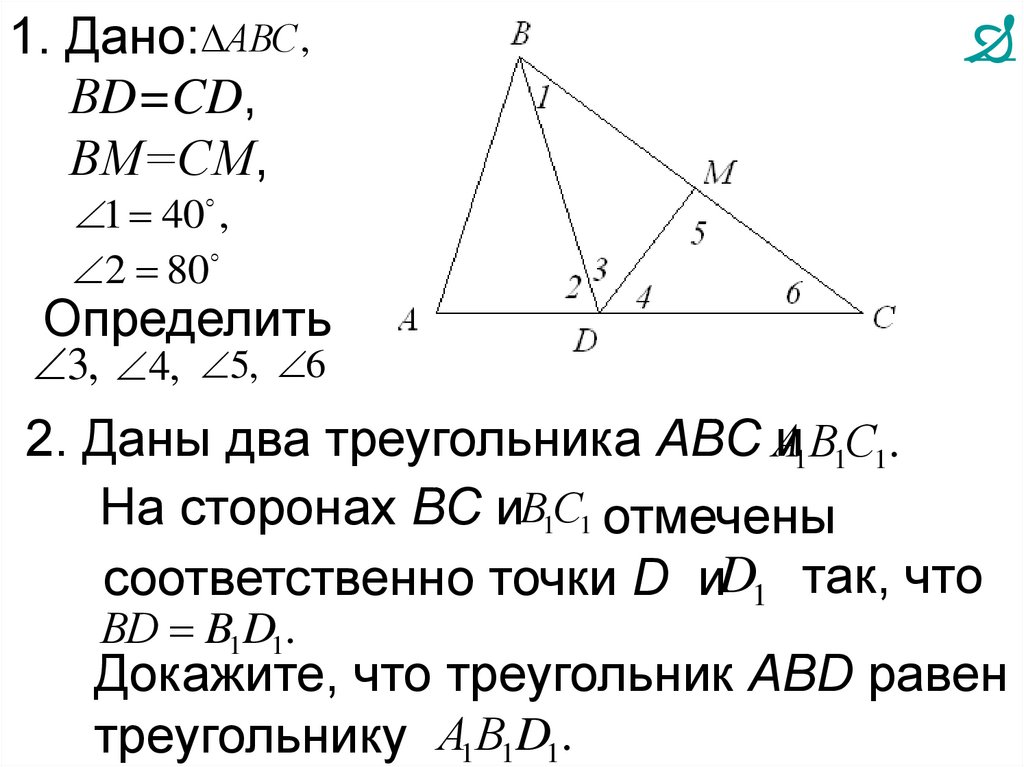
1. Дано: АВС ,
ВD=CD,
ВМ=СМ,
1 40 ,
2 80
Определить
3, 4, 5, 6
2. Даны два треугольника АВС А
и1В1С1.
На сторонах ВС иВ1С1 отмечены
соответственно точки D иD1 так, что
ВD B1D1.
Докажите, что треугольник АВD равен
треугольнику А1В1D1.

50.

1. Основание равнобедренного треугольни
в 3 раза меньше боковой стороны, а его
периметр равен 28 см.
Определите стороны треугольника.
2. В равнобедренном треугольнике АВС
с основанием АС С 30 , BD- медиана
Определите углы треугольника ABD.

51.

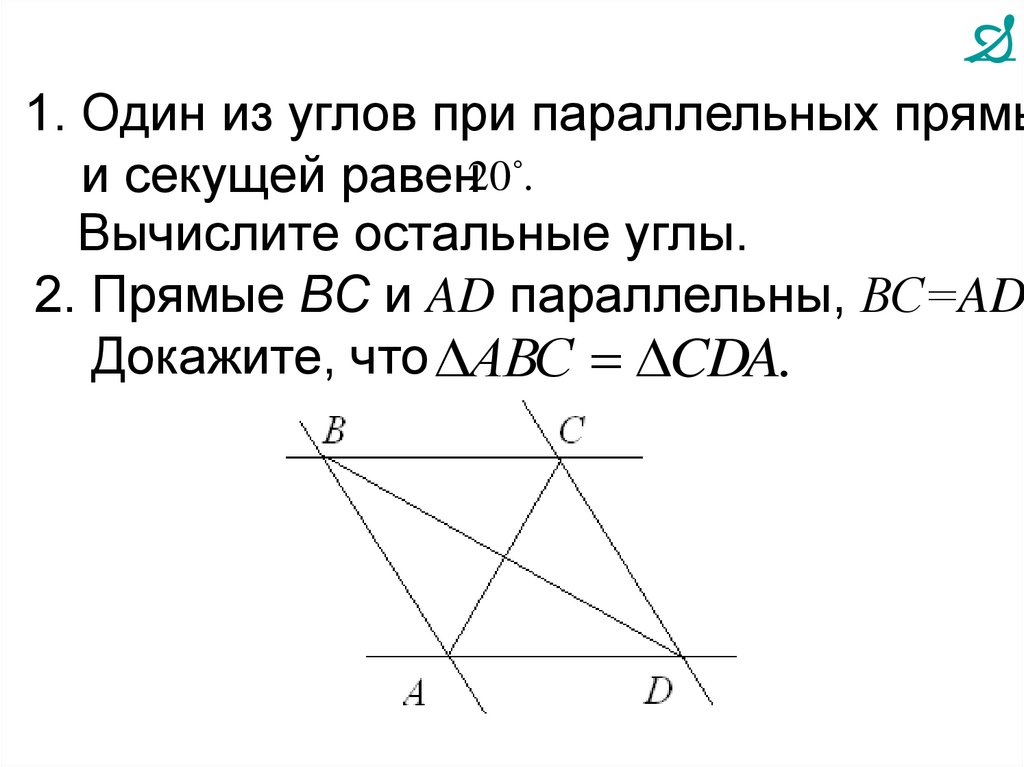
1. Один из углов при параллельных прямы
и секущей равен20 .
Вычислите остальные углы.
2. Прямые ВС и AD параллельны, ВС=AD
Докажите, что АВС CDA.

52.

Задача:
Углы треугольника пропорциональны числам
а) 2 : 3 : 5,
б) 1 : 3 : 6.
Вычислите углы треугольника.

53.

1. Хорды АВ и ВС равны.
Докажите, что
AOD BOC .
2. Радиус окружности равен 7 см.
АВ- касательная. AOB 60 . Найдите ОВ.

54.

1. Луч с проходит между сторонами угла
Найдите угол
(АВ), равного 40 .
(ас),
23
если
угол (bc)АВ
= длиной
.
2.
На отрезке
20 см отмечена
точка С. Найдите длину отрезка АС, есл
он больше отрезка ВС на 4 см.
3. Точки А, В и С лежат на одной прямой.
Известно, что АВ = 3 см, ВС = 5 см,
АС = 2 см. Принадлежит ли точка С
отрезку АВ? Объясните ответ.
4. Из точки А проведены лучи АМ, АN, АК.
Чему равен NAK, если MAN = 76,
MAK = 46 ?

55.

1. Один из углов, получившихся при пересечении двух
прямых, равен 85 . Вычислите остальные углы.
2. Разность смежных углов равна 50 .
Найдите меньший угол.
3. Один из двух углов, образовавшихся при пересечении
двух прямых, на 20 меньше другого. Найдите все
образовавшиеся углы.
4. Из вершины угла проведен луч, перпендикулярный его
биссектрисе и образующий со стороной данного угла
острый угол, равный 40 .
Найдите величину данного угла.

56.

1.На основании АС равнобедренного
треугольника АВС отложены равные
отрезки AD и CE. Докажите, что
BAD BCE.
2. Периметр равнобедренного треугольника равен 16,6 см.
Найдите его стороны, если основание больше боковой
стороны на 4 см.
3. На биссектрисе угла А взята точка В, а на сторонах угла
точки С и D, такие, что АВС АВD.
Докажите, что AD=AC.
4. Треугольники АВС и DBC
равнобедренные с основанием
ВС. Известно, что АВ=CD.
Докажите, что эти треугольники равны.

57.

1. Параллельные прямые а и b
пересечены прямой с,
1 122 .
Найдите 2.
2. В равнобедренном треугольнике MNK с основанием
MK внешний угол при основании в 4 раза больше
своего внутреннего. Вычислите углы треугольника.
3. Дано:
1 2.
Доказать:
а b.
4. Докажите равенство двух равнобедренных
треугольников по углу при основании и высоте,
проведенной к основанию.

58.

1. Отрезки MN и PK являются диаметрами окружности
с центром в точке А. Докажите, что хорды MP и NK
параллельны.
2. АС – касательная, а АВ – хорда
окружности с центром в точке О,
ВАС 75 . Чему равен АОВ ?
3. Постройте прямоугольный треугольник по гипотенуз
равной 4 см и острому углу, равному
45 .
4. Постройте с помощью циркуля и линейки угол,
равный 75 .