Похожие презентации:
Решение дробных рациональных уравнений. Проверка домашнего задания № 450
1. Проверка домашнего задания
№ 450На окружности отмечено 12 точек.
Сколько существует треугольников с
вершинами в этих точках?
Ответ: 220
2. Проверка домашнего задания
№ 451Сколькими способами можно составить из
партии, содержащей n деталей, комплект
из р деталей ( р<=n) для контроля за
качеством продукции?
Ответ: число сочетаний из n по p
3. Проверка домашнего задания
№ 451В школьном хоре 6 девочек и 4 мальчика.
Сколькими способами можно выбрать из
состава школьного хора 2 девочек и 1
мальчика для участия в выступлении
окружного хора?
Ответ: 60
4. Проверка домашнего задания
№ 459В вазе лежат 5 разных яблок и 6
различных апельсинов. Сколькими
способами из них можно выбрать 2
яблока и 2 апельсина?
Ответ:150
5. Проверка домашнего задания
№ 460Колода карт содержит по 13 карт каждой
из 4 мастей. Сколькими способами можно
выбрать из колоды следующий набор:
3 карты пиковой, 4 карты трефовой,5 карт
червовой, 2 карты бубновой масти ?
Ответ:
6. Тема урока: «Сочетания без повторений и бином Ньютона. Треугольник Паскаля»
7.
1623-1662 г.г.французский математик, физик, религиозный
философ и писатель.
8.
1643-1727 г.г.английский математик, механик, астроном и физик,
9. Актуализация знаний
1) Запишите степени суммы (а+в)10.
Составим таблицу коэффициентов(выписать на доску)
Сумма степеней каждого слагаемого равна степени бинома.
Число слагаемых на 1 больше степени бинома.
Коэффициенты симметричны.
11.
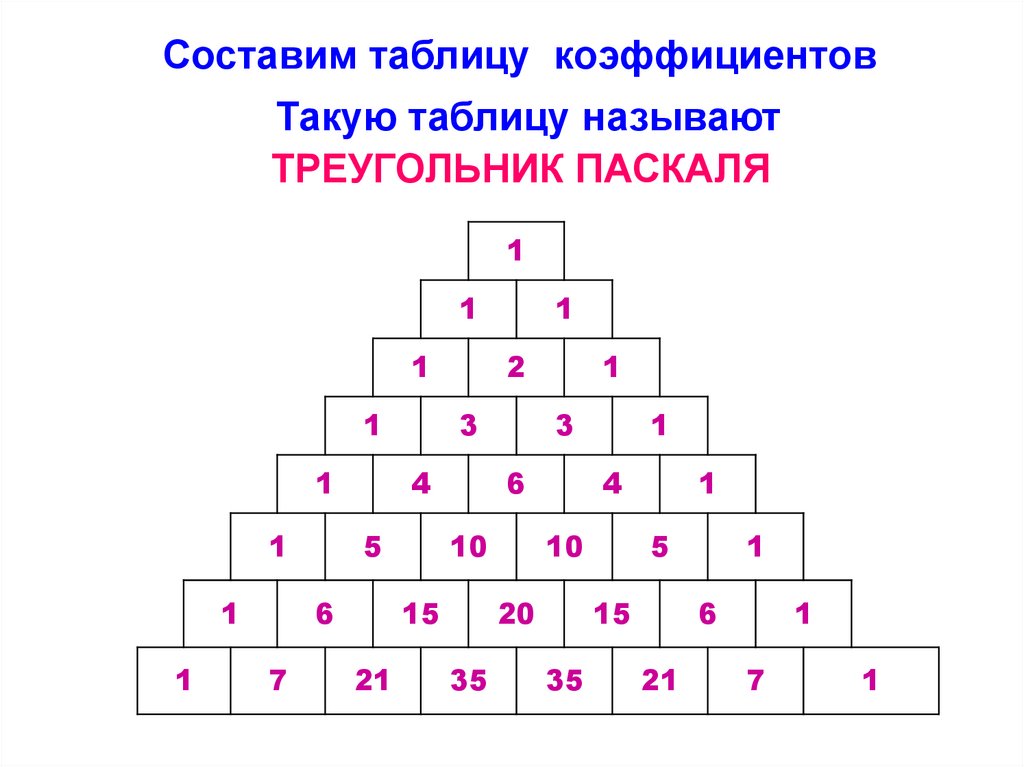
Составим таблицу коэффициентовТакую таблицу называют
ТРЕУГОЛЬНИК ПАСКАЛЯ
1
1
1
1
1
1
1
1
7
2
3
4
5
6
1
3
6
10
15
21
1
4
10
20
35
1
1
5
15
35
1
6
21
1
7
1
12.
Проблема!?
13.
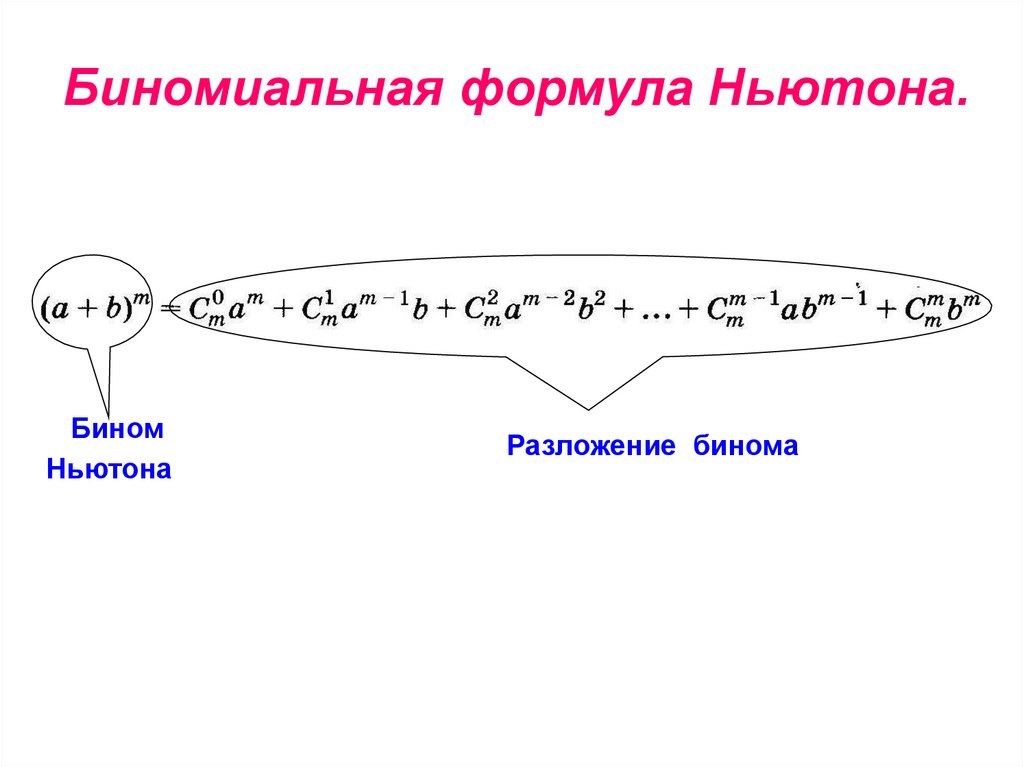
Биномиальная формула Ньютона.Бином
Ньютона
Разложение бинома
14.
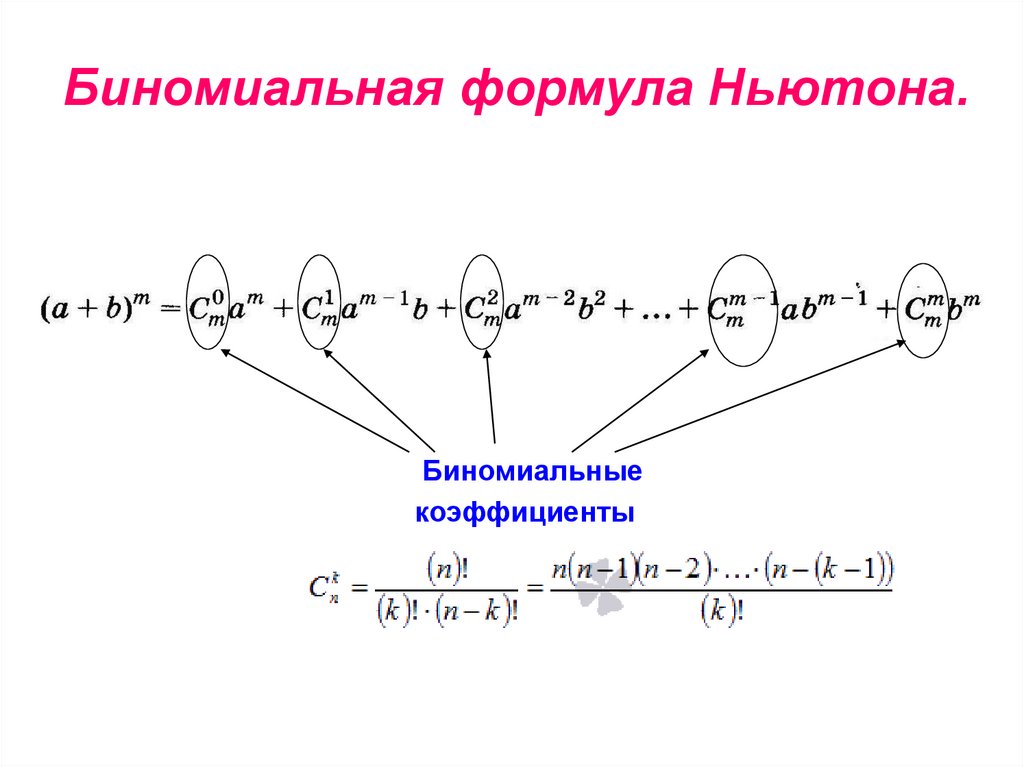
Биномиальная формула Ньютона.Биномиальные
коэффициенты
15.
Биномиальная формула Ньютона.общий член разложения бинома n-й степени
Tm 1 C nm a n m b m , m 0 ,1,2 ,...n
16.
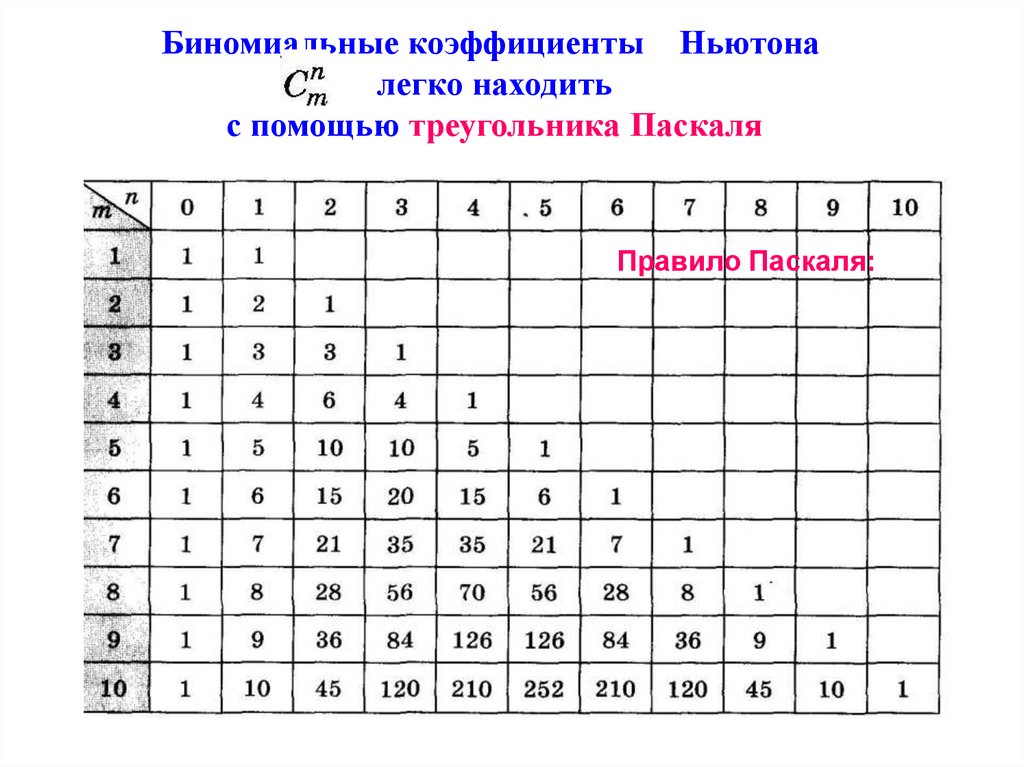
Биномиальные коэффициенты Ньютоналегко находить
с помощью треугольника Паскаля
Правило Паскаля:
17.
1)Число слагаемых на 1 больше степени бинома.
2) Коэффициенты находятся по треугольнику
0
n
Паскаля, причём С n С n 1
3)
Коэффициенты симметричны.
С nm C nn m
Сумма степеней каждого слагаемого равна степени
бинома.
5) общий член разложения бинома n-й степени
4)
6)
18. Записать разложение бинома:
Решениезадач
Записать
разложение
бинома:
19. №455(1,3), 456(2), 462
Решениезадач
№455(1,3), 456(2),
462
20. Вариант1 №452(1), 455(2),456(1), 461
Вариант1Самостоятельная
работа
№452(1), 455(2),456(1), 461
Вариант2
№452(2), 455(4),456(1), 461
21. Проверка
Вариант1№ 452(1)
1+7х+21х2+35х3+35х4+21х5+7х6+х7
№ 455(2)
220
№ 456(1)
32
№ 461
120х2
22. Проверка
Вариант2№ 452(2) х -8х +24х -32х+16
4
3
№ 455(4)
4950
№ 456(1)
32
№ 461
120х2
2
23. Домашнее задание
Параграф5,№452(5,6)
№457
№464
24. Дополнительный материал
• http://www.youtube.com/watch?v=fRKaKy4i5t4
• http://vuroki.ru/urok/63/225




















 Математика
Математика








