Похожие презентации:
Сложное сопротивление
1.
Санкт-Петербургский государственныйархитектурно-строительный университет
кафедра Строительной механики
Лекция 5.
Сложное сопротивление стержней. Косой изгиб
Авторы:
к.т.н., Войтко Александр Михайлович
1
2.
Сложное сопротивление – такой вид деформации, при котором в стержне могут возникнуть все шестьвидов внутренних усилий одновременно.
Среди случаев сложного сопротивления стержней наиболее часто встречаются следующие сочетания
простых видов нагружения: косой изгиб (см. рисунок, а), внецентренное растяжение или сжатие (см.
рисунок, б) и одновременное действие кручения с изгибом (см. рисунок, в), изгиб с растяжением или
сжатием и т. д.
Для изгибающих моментов принимается другое
правило знаков, а именно, изгибающий момент считается
положительным, если он вызывает растягивающие
напряжения в положительном квадранте (т. е. в том
квадранте, где координаты y > 0 и z > 0 ).
Поперечная сила считается положительной, если она
направлена по направлению оси y (или z ) и действует в
сечении, внешняя нормаль к которому совпадает по
направлению с осью x .
Правила знаков для внутренних усилий в задачах сложного
2
3.
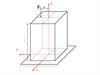
Косым изгибом называется такой вид сложногосопротивления,
при
котором
плоскость
действия изгибающего момента в поперечном
сечении бруса не проходит ни через одну из
главных центральных осей этого сечения, или
не совпадает ни с одной из главных плоскостей
Пространственный косой
изгиб
А) прямоугольное сечение;
Б) сечение прокатного
профиля
3
4.
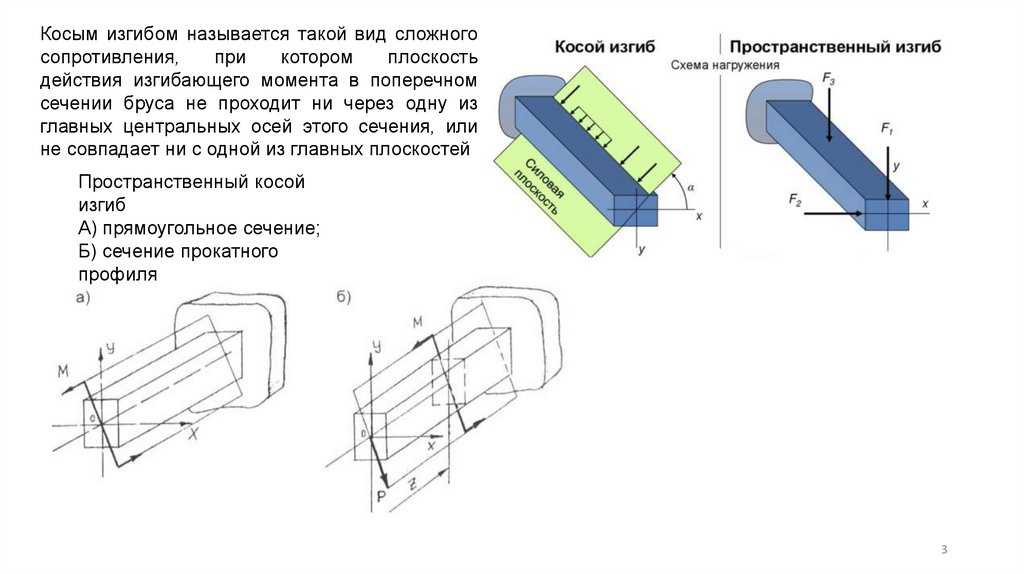
Под главной плоскостью понимают плоскость,проходящую через про- дольную ось балки и одну из
главных центральных осей поперечного сечения.
Например, для прямоугольного сечения (см. рисунок,
г) – это плоскости, проходящие через оси ZX, YX.
Косой изгиб можно подразделить на плоский и
пространственный. Плоский косой изгиб – это вид
сложного сопротивления, когда все внешние силы
расположены в одной плоскости (см. рисунок, а),
называемой силовой, и эта плоскость не совпадает ни
с одной из главных плоскостей.
Пространственный косой изгиб отличается от плоского
лишь тем, что внешние силы не находятся в одной
плоскости и изогнутая ось балки будет уже не плоской,
а пространственной кривой. Плоский косой изгиб
представляет
собой
частный
случай
пространственного изгиба.
4
5.
где уD и zD – координаты точки.Все параметры, входящие в эту формулу, подставляются по модулю, а знаки перед составляющими
слагаемыми определяем из физических соображений: если изгибающий момент Мz или Му вызывает
в точке растягивающее напряжение, то перед составляющей должен быть знак плюс, сжимающее
напряжение – знак минус.
Опасные точки в сечении при косом изгибе определяются по положению нейтральной линии.
Нейтральная линия – это геометрическое место точек, в которых нормальные напряжения равны
нулю.
5
6.
Для сечений типа прямоугольного, двутавра, швеллера и т.д. имеющих ярко выраженныеугловые точки, условие прочности можно записать в виде:
Для хрупких материалов условие прочности записывают для двух опасных точек, наиболее
удалённых от нейтральной линии (точки В и т. D):
6
7.
При расчете бетона условия прочности имеют вид:где Rt , Rс - соответственно расчетные сопротивления бетона осевому растяжению и сжатию.
Порядок проверки прочности балки, работающей в условиях косого или пространственного изгиба, тот же, что
и для балки, работающей при плоском поперечном изгибе. Для этого необходимо:
• построить эпюры внутренних усилий. Для построения эпюр внутренних усилий раскладываем нагрузки на
вертикальную и горизонтальную составляющие. Вертикальная составляющая вызывает изгиб относительно
горизонтальной оси y, горизонтальная – относительно оси z;
• выбрать опасные сечения – это сечения, где имеет место наиболее неблагоприятное сочетание изгибающих
моментов;
• в опасных сечениях найти опасные точки – точки с максимальными нормальными напряжениями;
• записать условие прочности в этих точках. Из условия прочности либо подобать размеры поперечного
сечения, либо найти допускаемую нагрузку, либо просто сделать вывод о возможности безопасной
Вертикальная составляющая полного прогиба w
эксплуатации конструкции.
находится по формуле
Перемещения v точек оси балки вдоль оси y,
вызванные горизонтальной составляющей нагрузки,
определяются аналогично
7
8.
89.
910.
1011.
1112.
0,19 см0,33 см
12
13.
F1 = 60 кНF2 = 10 кН
M = 20 кН⋅м
10° к оси z
Эпюры изгибающих моментов от:
а, б – вертикальной составляющей нагрузки;
в, г – горизонтальной составляющей нагрузки;
д, е – единичной силы
13
14.
Убедимся в том, что условие прочности выполняется и в опасных точках опасного сеченияD:
EIywC = 700,8кН⋅м3. EIzvC = 105,8 кН⋅м3
14
15.
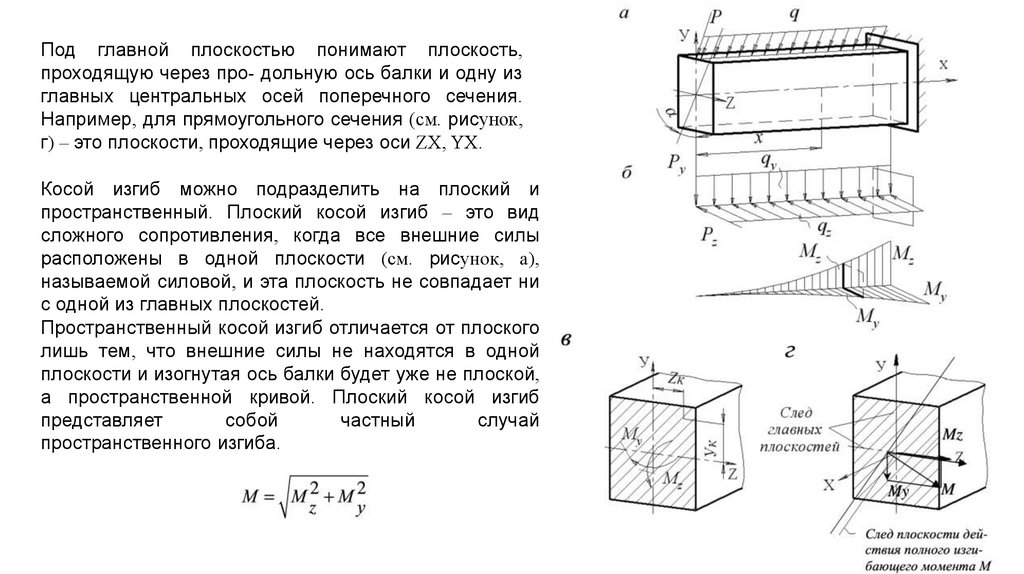
или 0,118z + 1,386 y = 0Таким образом, угол между полным
перемещением CC′ и нейтральной
линией 4,9° + 80,9° = 85,8°, что близко к
90°.
15
16.
Санкт-Петербургский государственныйархитектурно-строительный университет
кафедра Строительной механики
Авторы:
к.т.н., Войтко Александр Михайлович
tehmeh@spbgasu.ru
16













 Механика
Механика