Похожие презентации:
Сложное сопротивление. Энергия деформации при изгибе
1. Энергия деформации при изгибе
Наиболее общий метод определенияперемещений в упругих системах —
энергетический.
В основу этого метода положено условие
равенства работы внешних сил,
приложенных к линейнодеформируемой упругой системе,
и энергии деформации системы
2. Теорема Клапейрона:
«Работа статически приложеннойвнешней силы (момента пары сил)
равна половине произведения
конечного значения силы
(момента пары сил)
на конечное значение
соответствующего перемещения
(угла поворота)»
3.
КлапейронБенуа Поль Эмиль
(1799 - 1864)
Французский механик и
инженер.
В Институте корпуса
инженеров путей
сообщения в
Петербурге 11 лет
преподавал
аналитическую и
прикладную механику,
химию и строительное
искусство
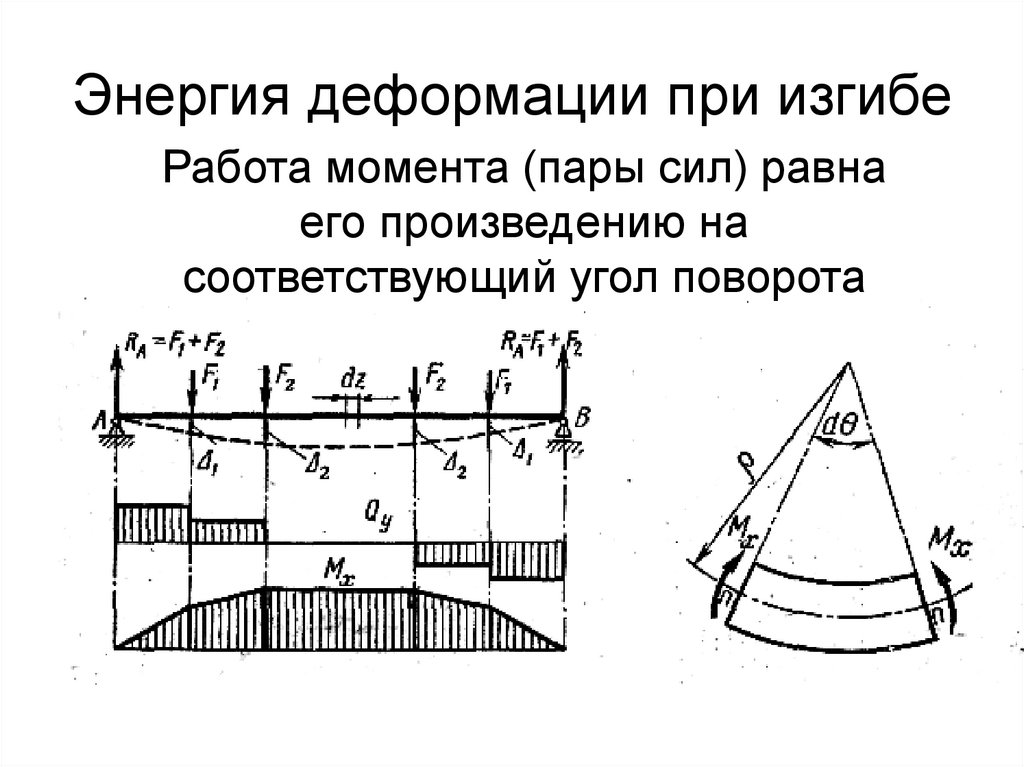
4. Энергия деформации при изгибе
Работа момента (пары сил) равнаего произведению на
соответствующий угол поворота
5.
По теореме Клапейрона1
dV dW M x d ;
2
dz
d ;
M
dz
x
d
;
EJ x
1/ M x /( EJ x );
2
x
M dz
dV
2EJ x
6. Для вычисления энергии деформации балки в целом следует просуммировать значения dV по всей ее длине. При этом следует учесть,
чтозакон изменения изгибающих моментов для
отдельных участков балки различен,
поэтому вычисление определенных интегралов
надо вести отдельно для каждого участка длиной li,
а затем результаты суммировать:
2
x
M dz
V
2
EJ
x
i 1 l
n
i
7. Косой изгиб -
Косой изгиб вид деформации, характеризующийсяизменением кривизны бруса под
действием внешних сил, проходящих
через его ось и не совпадающих ни с
одной из главных плоскостей.
8.
9. Косой изгиб удобнее всего рассматривать как одновременный изгиб бруса в двух главных плоскостях zOх и zOy.
Для этого изгибающий момент M изграскладывается на составляющие
моменты относительно осей х и у:
M x M изг sin ;
M y M изг cos
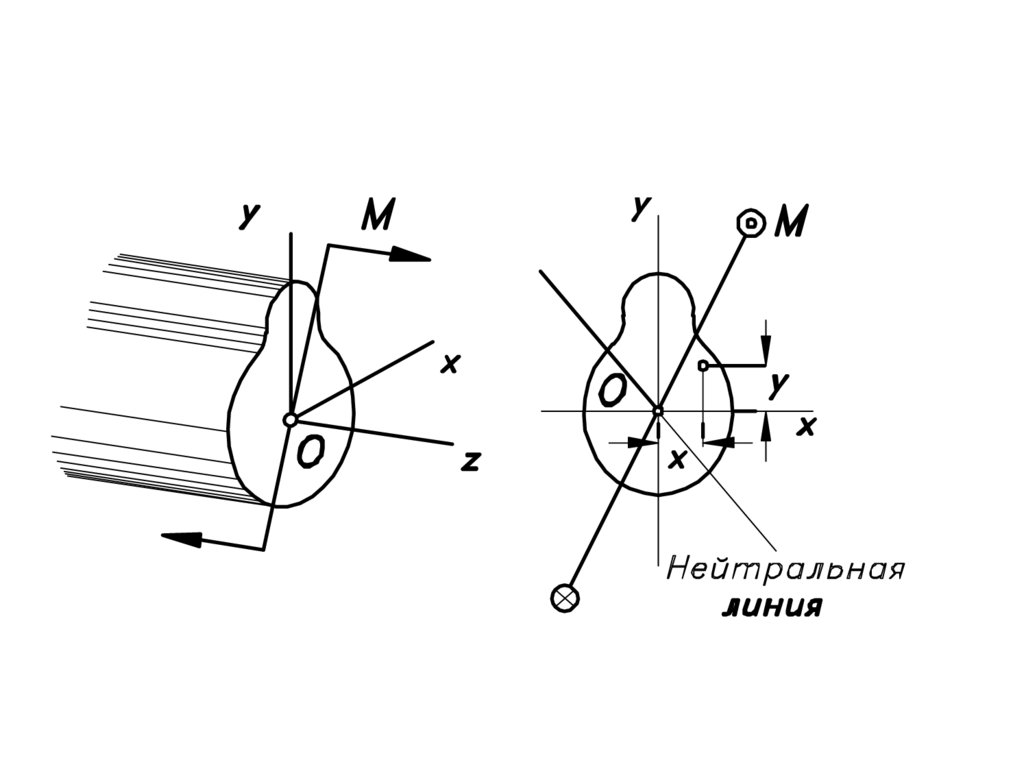
10. Нормальное напряжение в точке с координатами х и у определяется по формуле:
Mx y M y xJx
Jy
y
x
M изг ( sin cos )
Jx
Jy
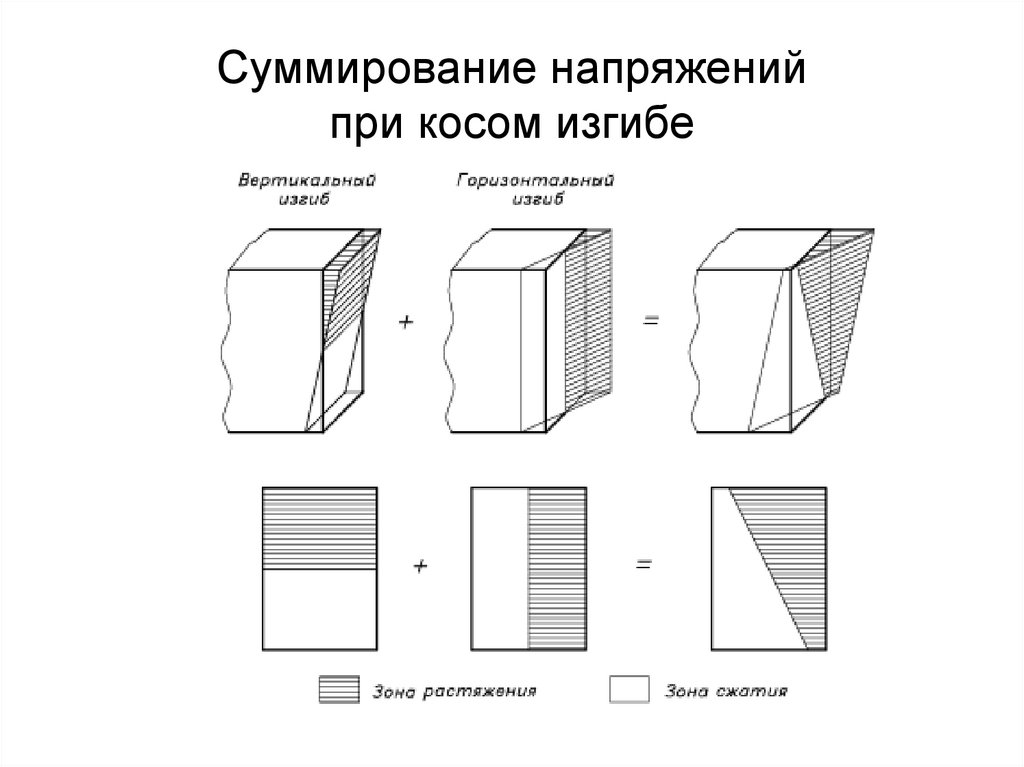
11. Суммирование напряжений при косом изгибе
12. Уравнение нейтральной линии (σ = 0)
yx
M изг ( sin cos ) 0
Jx
Jy
y
x
sin cos 0
Jx
Jy
Jx
y x
Jy
ctg
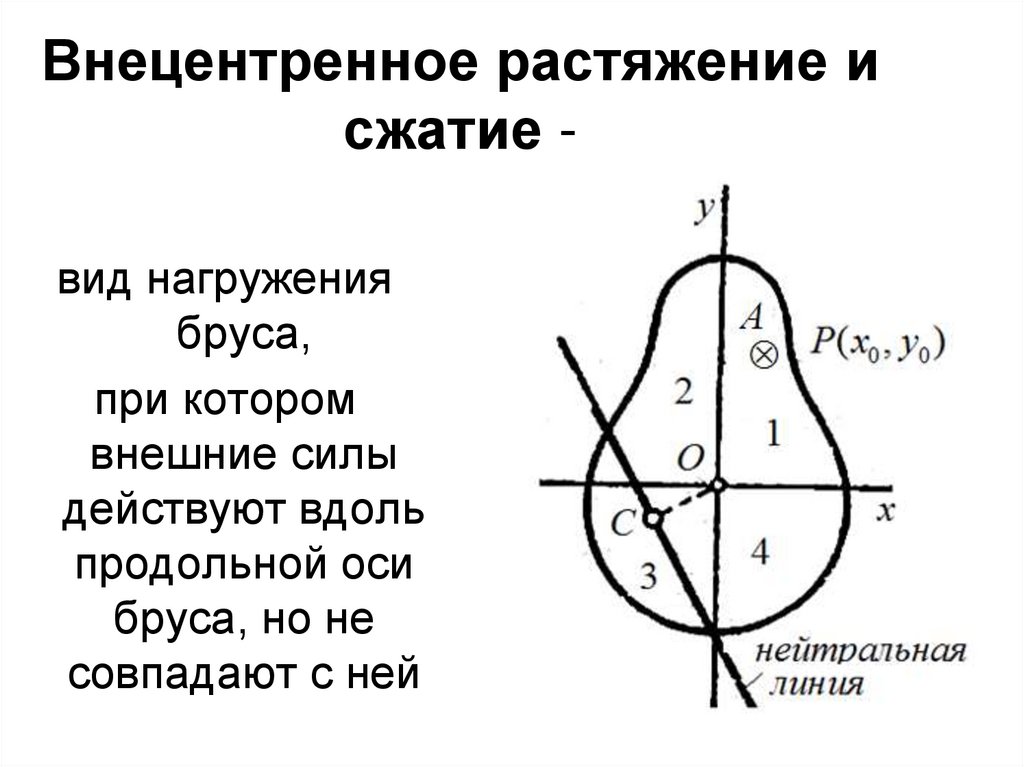
13. Внецентренное растяжение и сжатие -
Внецентренное растяжение исжатие вид нагружения
бруса,
при котором
внешние силы
действуют вдоль
продольной оси
бруса, но не
совпадают с ней
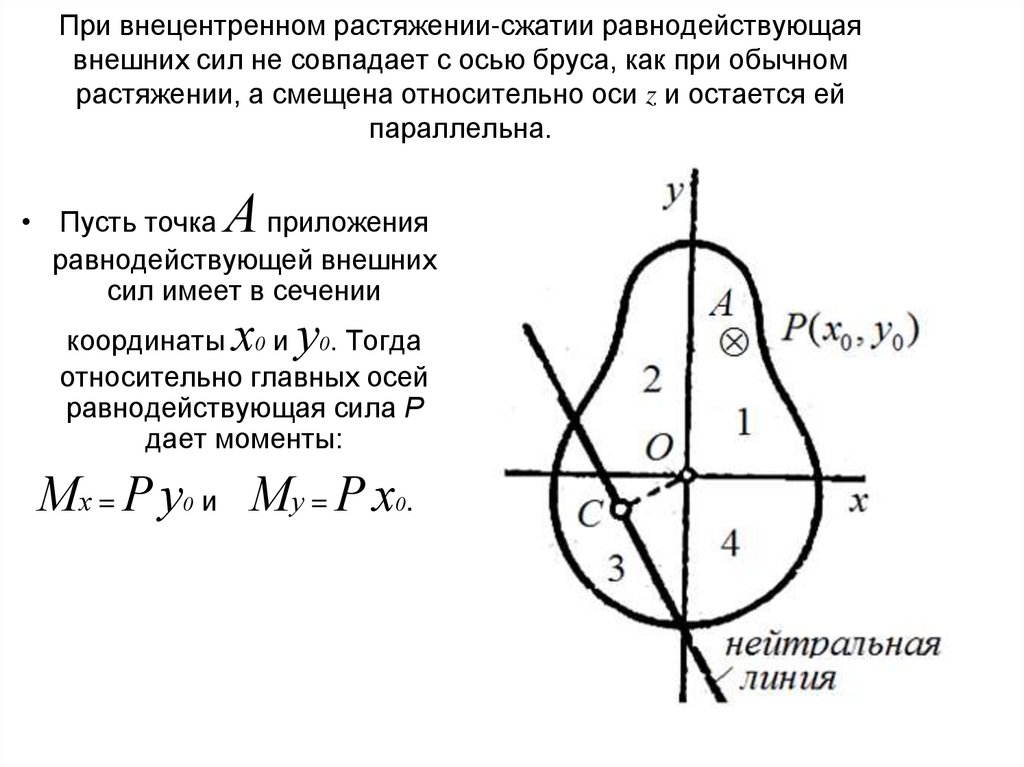
14. При внецентренном растяжении-сжатии равнодействующая внешних сил не совпадает с осью бруса, как при обычном растяжении, а
смещена относительно оси z и остается ейпараллельна.
А
• Пусть точка
приложения
равнодействующей внешних
сил имеет в сечении
х у
координаты 0 и 0. Тогда
относительно главных осей
равнодействующая сила Р
дает моменты:
Мх = Р у
0
и
Му = Р х .
0
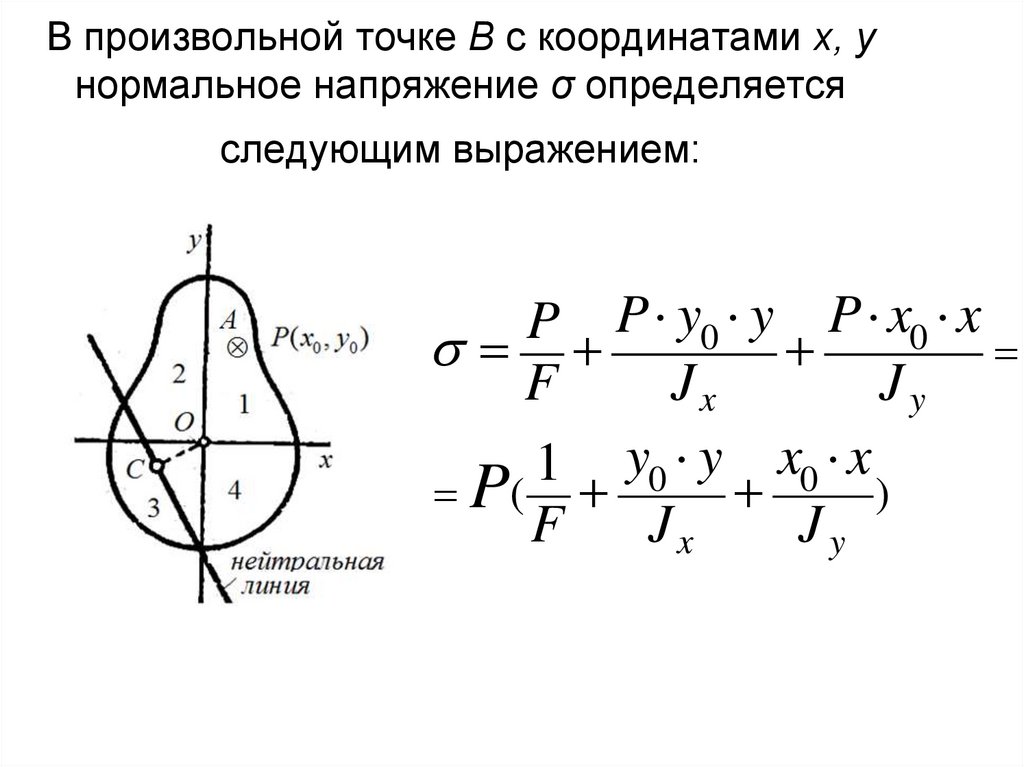
15. В произвольной точке В с координатами х, у нормальное напряжение σ определяется следующим выражением:
P P y0 y P x0 xF
Jx
Jy
1 y0 y x0 x
P(
)
F
Jx
Jy
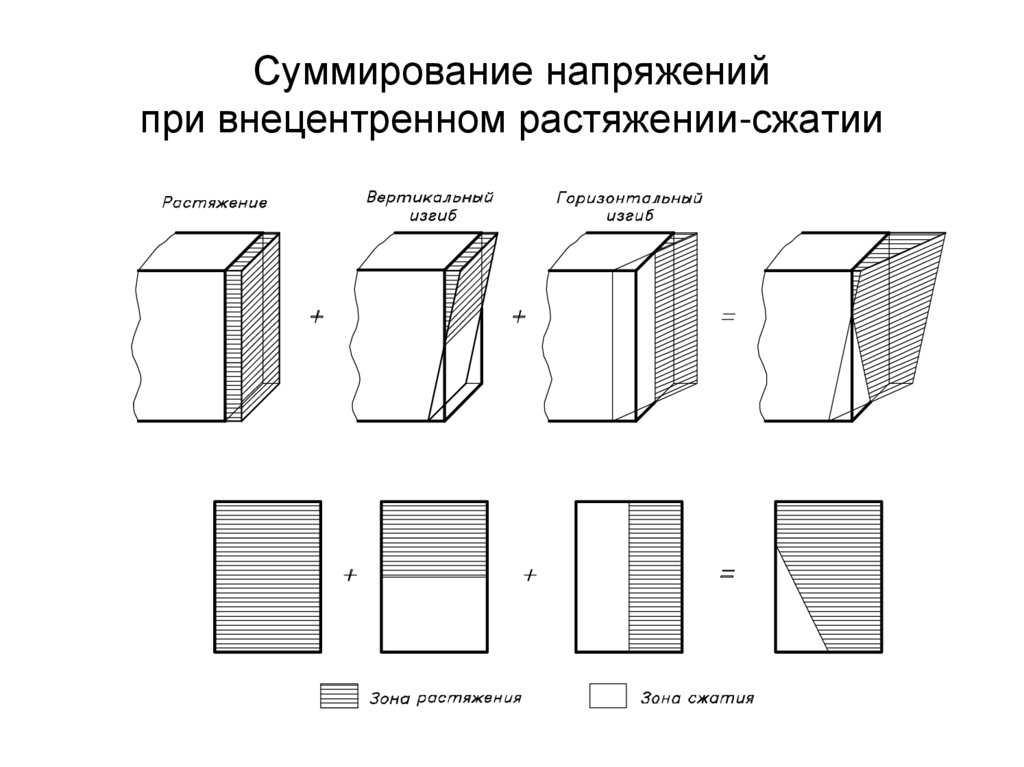
16. Суммирование напряжений при внецентренном растяжении-сжатии
17. При внецентренном растяжении — сжатии в отличие от косого изгиба нейтральная линия не проходит через центр тяжести сечения
1 y0 y x0 x0
F
Jx
Jy
18.
Из курса аналитической геометрии известно,что расстояние от начала координат
до некоторой прямой
ay bx c 0
равно величине
c
OC
.
a 2 b2
1/ F
OC
.
y0 2
x0 2
( ) ( )
Jx
Jy
19.
При внецентренном растяжении и сжатиинейтральная линия может как пересекать
сечение, так и находиться за его
пределами.
В первом случае в сечении возникают и
растягивающие, и сжимающие
напряжения.
Во втором случае напряжения во всех
точках сечения будут одного знака.
20. ЯДРО СЕЧЕНИЯ-
ЯДРО СЕЧЕНИЯобласть вокруг центра тяжестипоперечного сечения стержня.
Продольная сила, приложенная к любой
точке ядра сечения, вызывает в
сечении напряжения одного знака.
21. Конструкция ствола дерева предварительно напряжена. Каким-то образом дерево ухитряется расти так, что внешние слои древесины
растянуты,а внутренние сжаты
а) — поведение под ветром дерева,
в древесине которого нет
предварительных напряжений;
распределение напряжений по
сечению ствола линейно и
наибольшие растягивающие и
сжимающие напряжения одинаковы;
б) — предварительно напряженное
дерево в безветренную погоду;
наружные слои ствола растянуты,
внутренние — сжаты;
в) — предварительно напряженное
дерево при сильном ветре;
сжимающие напряжения
уменьшились наполовину, так что
дерево может выдержать вдвое
большие нагрузки, чем в случае а) .
22. Останкинская телебашня
Внутри по окружности ствола Останкинскойтелевизионной башни сверху донизу натянуты
стальные канаты.
Каждый из 150 канатов растянут с силой в 70 тонн.
Тело Останкинской башни сжато с силой в
десять с половиной тысяч тонн.
Башня способна выдержать
землетрясение магнитудой 8
по шкале Рихтера
(в Спитаке было 4–5)
и порывы ветра
со скоростью до 44 м/с (160 км/ч).
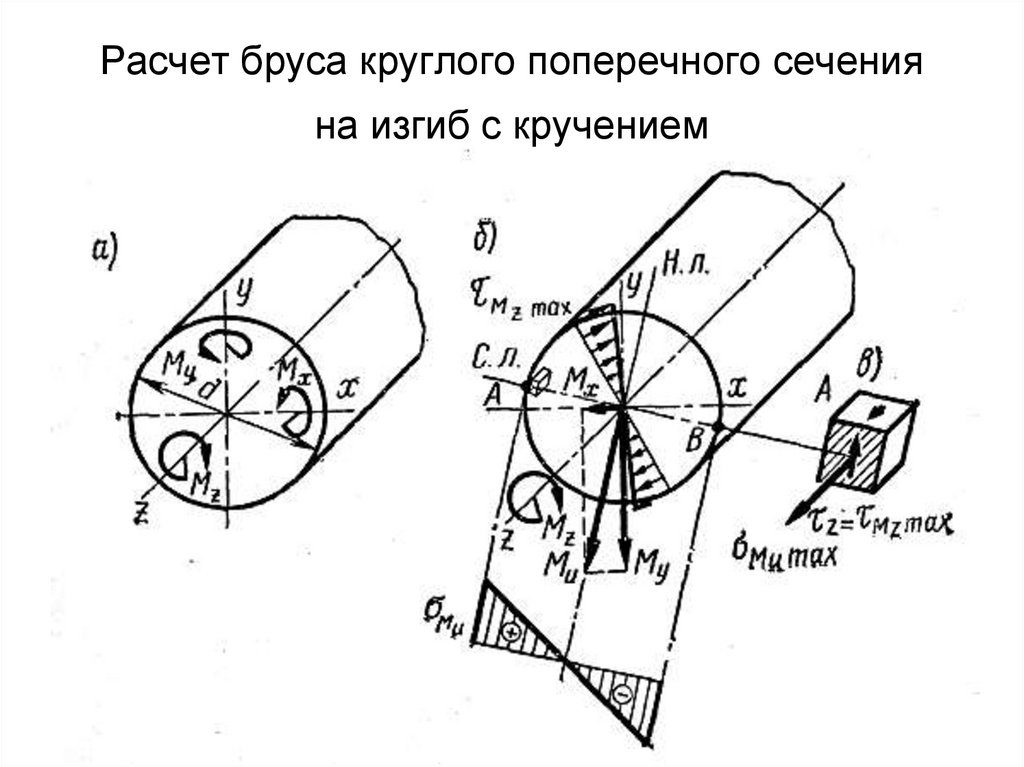
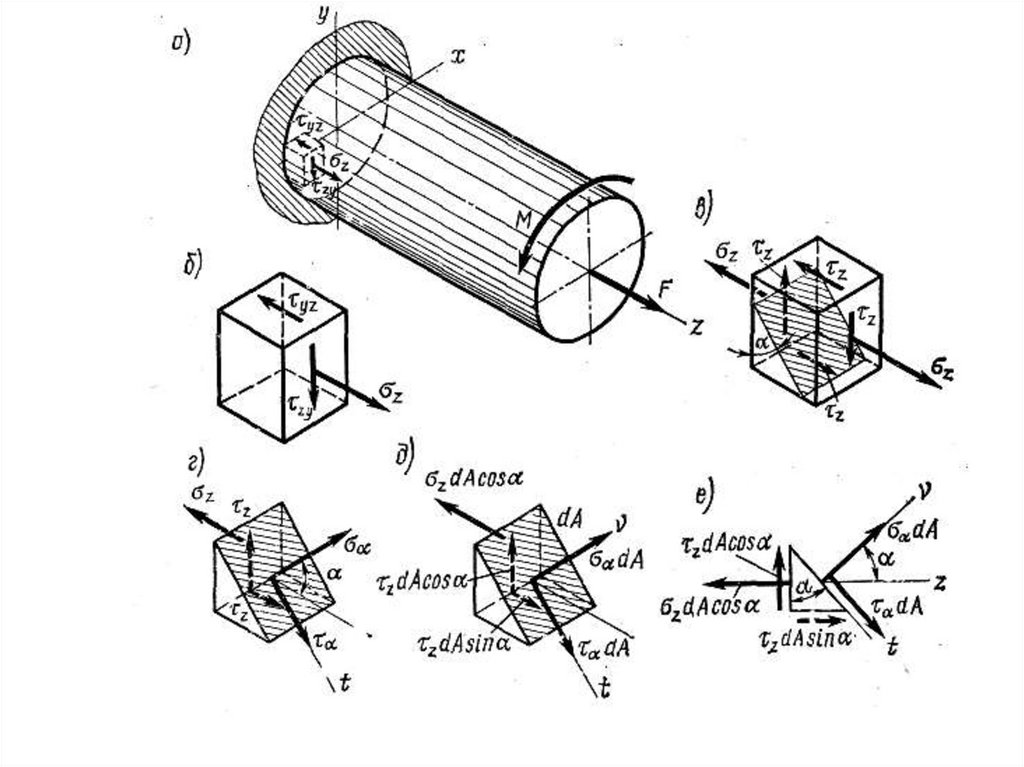
23. Расчет бруса круглого поперечного сечения на изгиб с кручением
24.
25.
26.
27.
28. По гипотезе наибольших касательных напряжений
эIII 42
z
2
z
29.
z МИ max
МИ
Мz
; z М И max
WИ
WP
2
эIII
МИ
Мz
4
WИ
WP
2
30.
2эIII
Экв
2
МИ
Мz
4
WИ
2WИ
М Экв
[ ].
WИ
М И2 М z2 М Экв
;
WИ
WИ
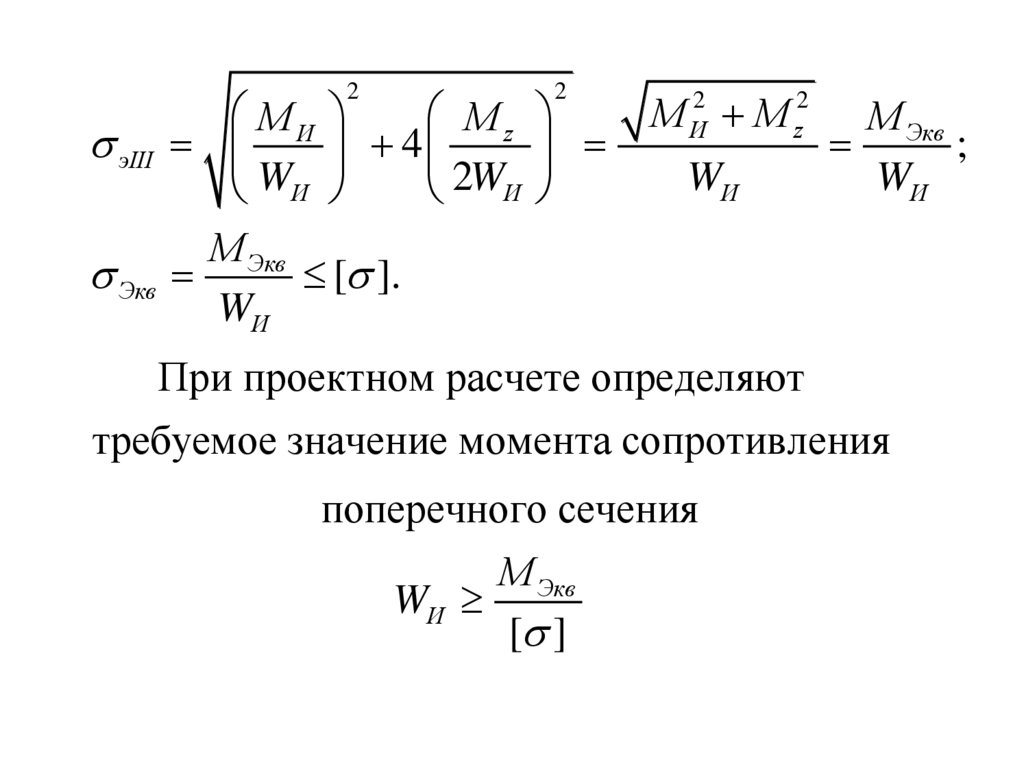
При проектном расчете определяют
требуемое значение момента сопротивления
поперечного сечения
М Экв
WИ
[ ]
31.
Учитывая, что для сплошного круглого сеченияWИ d / 32 0,1d
3
3
получаем следующую формулу для определения требуемого диаметра
вала:
32. Полярный момент инерции и момент сопротивления кручению сплошного круглого сечения
J P 2dA 2d dA
A
D/2
2
0
0
3 d d
3
d d
A
D 0,1D4.
4
32
WP
D
16
3
0,2D3








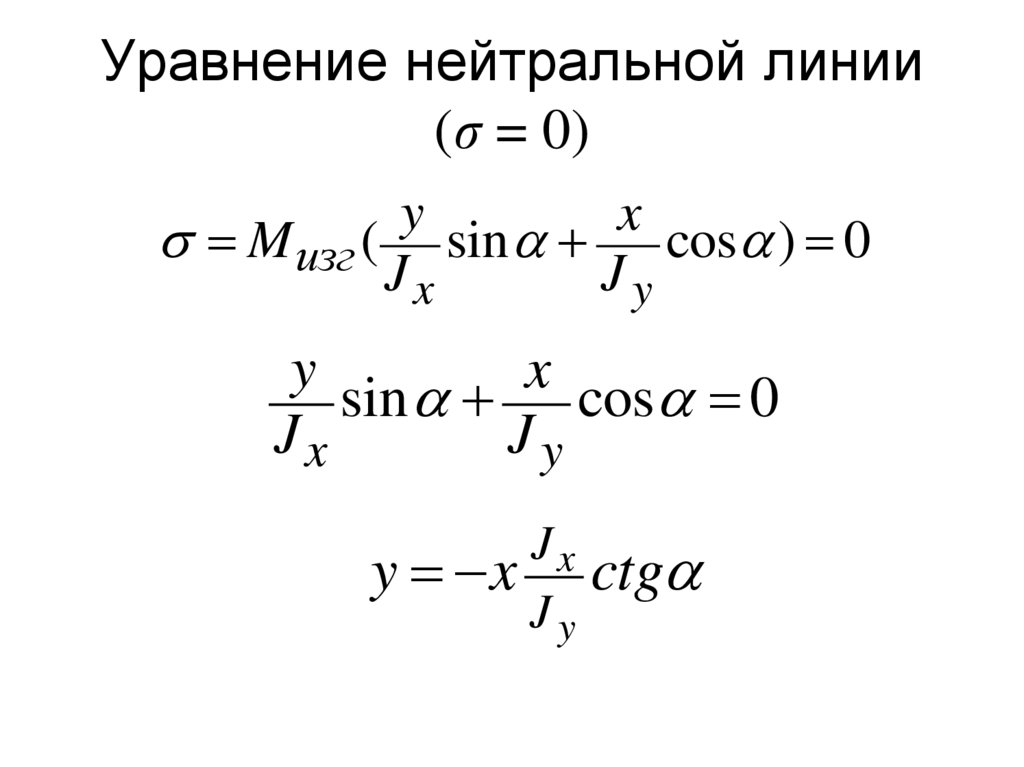






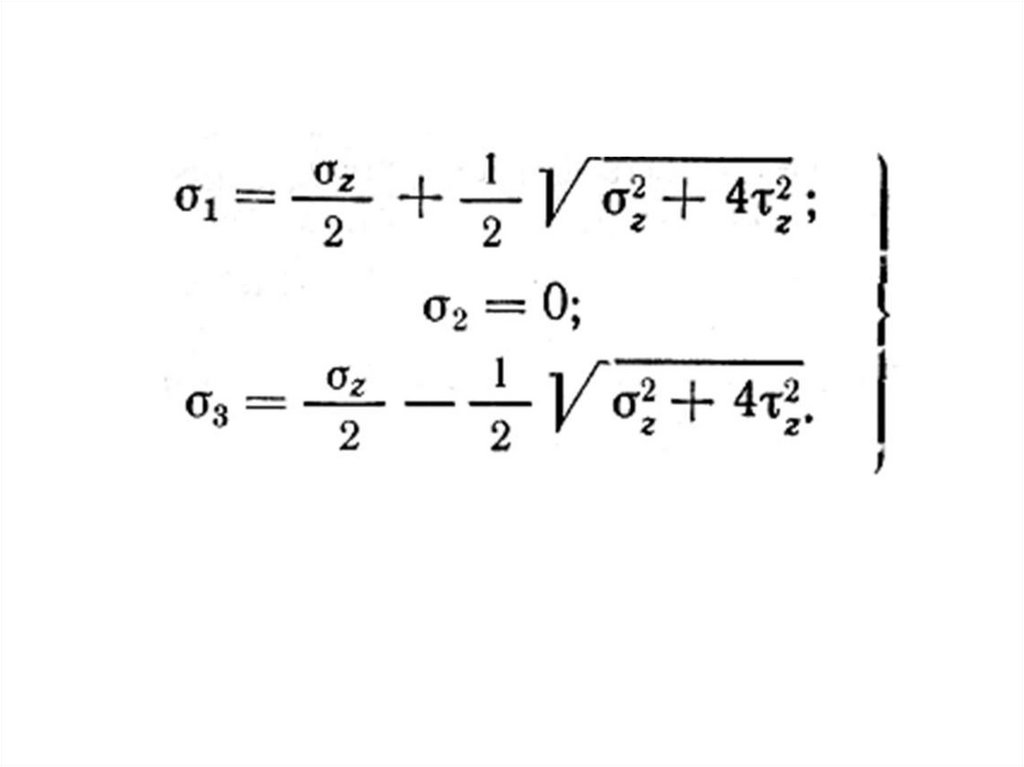
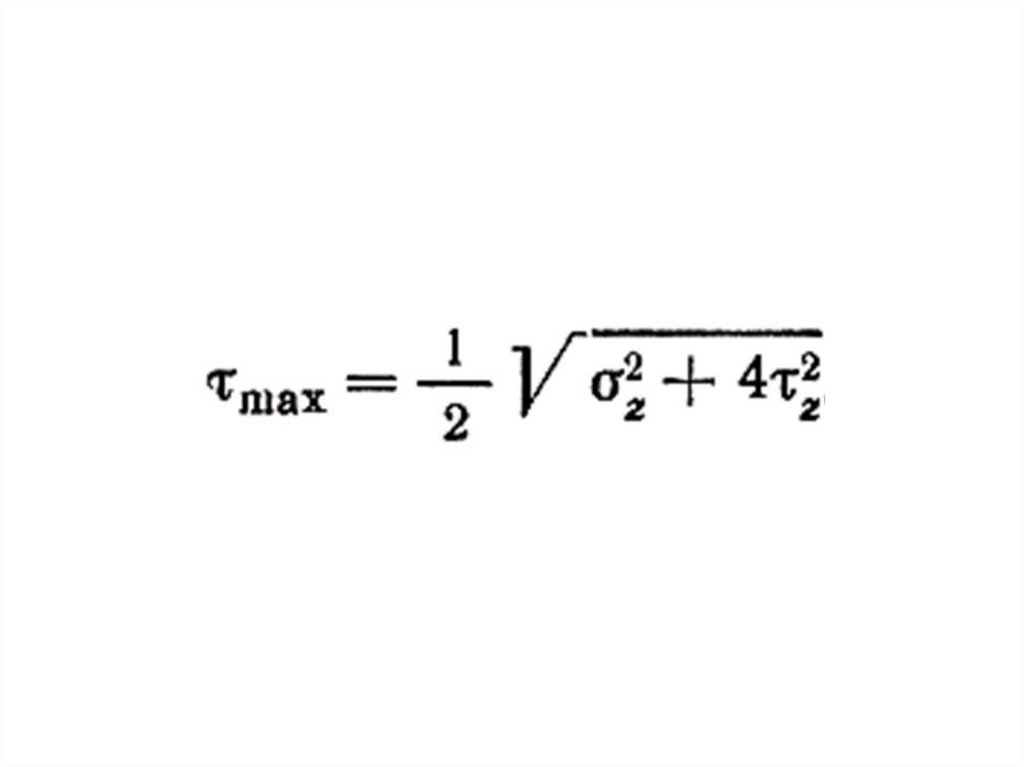

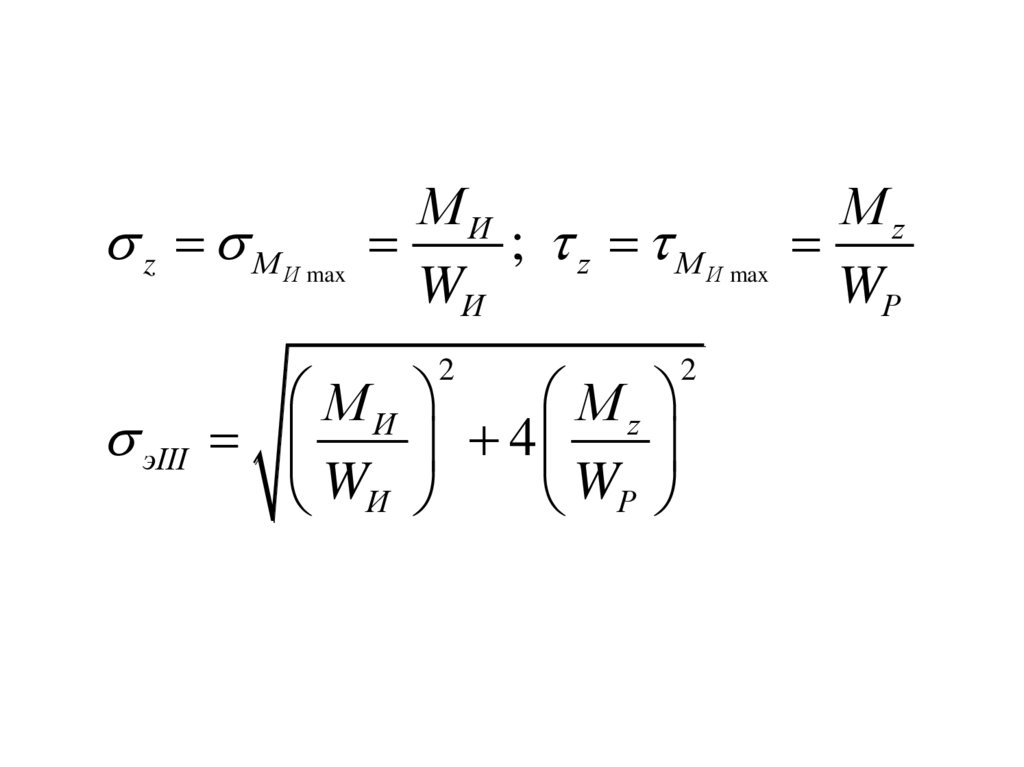


 Механика
Механика