Похожие презентации:
Итерационные методы решения СЛАУ
1.
Федеральное государственное бюджетное образовательное учреждениевысшего профессионального образования
«Ижевский государственный технический университет
имени М. Т. Калашникова»
Кафедра «АСОИУ»
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
Автор Исенбаева Е.Н., старший преподаватель
Ижевск
2013
2. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ(СЛАУ)
Итерационные методы - методы,в которых решение может быть
получено с заданной точностью
путем сходящихся бесконечных
процессов.
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
2
3. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ(СЛАУ)
Размерность системывелика
используют итерационные
методы
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
3
4. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ(СЛАУ)
Итерационные методы:–метод простых итераций
–метод Зейделя
–метод релаксации
– метод Шульца
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
4
5. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ
Решить систему линейных алгебраическихуравнений итерационными методами.
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
5
6. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
6
7. ПРИВЕДЕНИЕ СЛАУ К НОРМАЛЬНОМУ ВИДУ
Преобразуем систему (1) тем илииным способом к системе вида
х = αх+β
(2),
где х- тот же вектор неизвестных,
α, β – некоторые новые матрица и
вектор соответственно.
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
7
8. ПРИВЕДЕНИЕ СЛАУ К НОРМАЛЬНОМУ ВИДУ
Система (2):-приведена к нормальному виду
-пригодна для итерационного
процесса.
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
8
9. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ
• Используя систему (2),определяем последовательность
приближений
к неподвижной
точке х* рекуррентным
равенством
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
9
10. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ
• Метод простых итераций(МПИ)итерационный процесс (3),начинающийся с некоторого
вектора:
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
10
11. ПРИБЛИЖЕНИЯ К РЕШЕНИЮ СЛАУ
x( k 1)
2
x
(k )
21 1
22 x
(k )
2
... 2 n x
(k )
n
2
…
x
( k 1)
n
x
(k )
n1 1
n2 x
(k )
2
... nn x
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
(k )
n
n
11
12. ВЫБОР НАЧАЛЬНОГО ПРИБЛИЖЕНИЯ
Сходимость МПИгарантирована при любом
начальном векторе
.
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
12
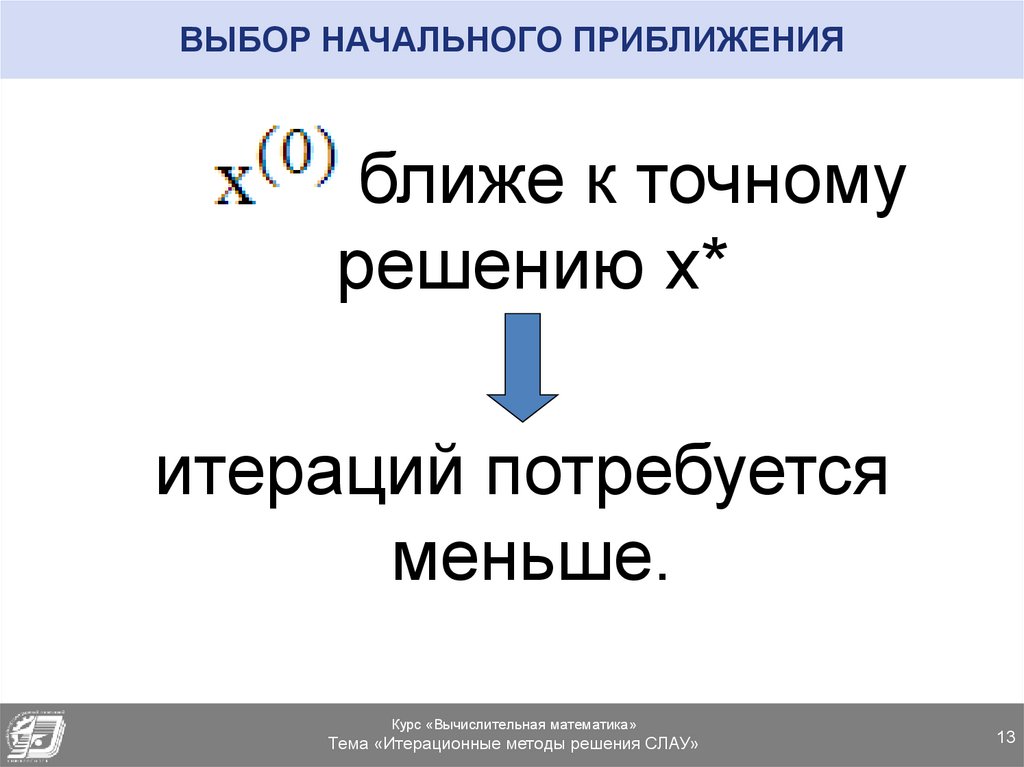
13. ВЫБОР НАЧАЛЬНОГО ПРИБЛИЖЕНИЯ
ближе к точномурешению х*
итераций потребуется
меньше.
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
13
14. ВЫБОР НАЧАЛЬНОГО ПРИБЛИЖЕНИЯ
Нет никакой информации о грубомрешении задачи (2) или решении
близкой задачи → за
обычно
принимают вектор β свободных
членов системы (2).
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
14
15. СПОСОБЫ ПРИВЕДЕНИЯ СЛАУ К НОРМАЛЬНОМУ ВИДУ
Диагональное преобладание:Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
15
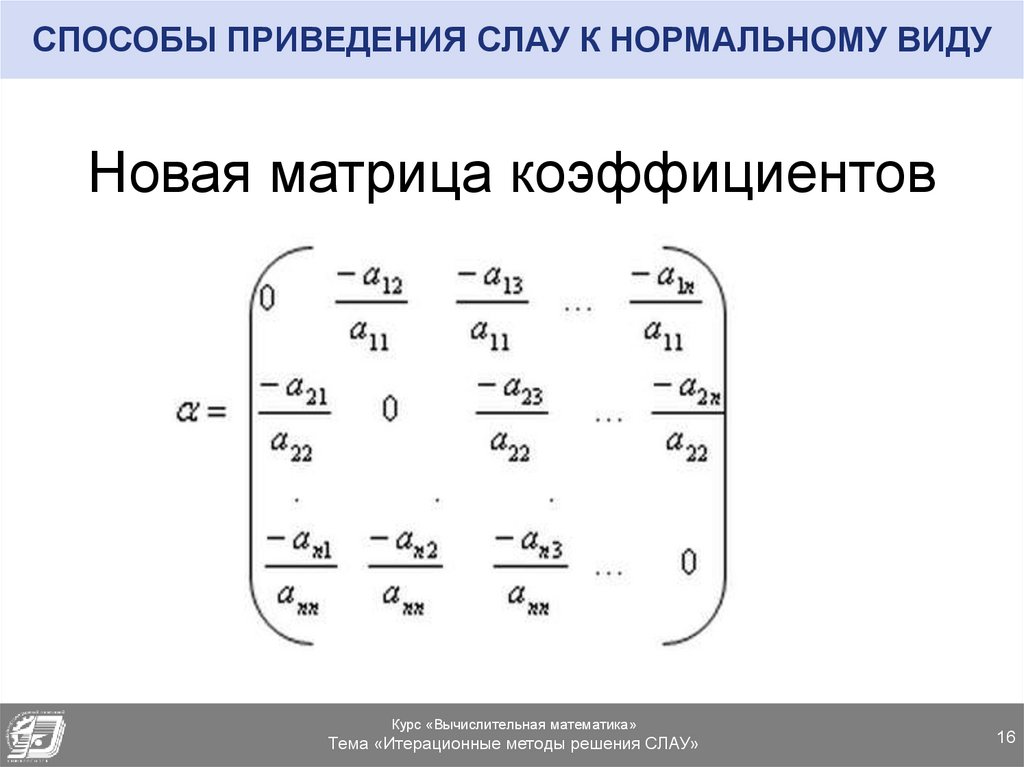
16. СПОСОБЫ ПРИВЕДЕНИЯ СЛАУ К НОРМАЛЬНОМУ ВИДУ
Новая матрица коэффициентовКурс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
16
17. СПОСОБЫ ПРИВЕДЕНИЯ СЛАУ К НОРМАЛЬНОМУ ВИДУ
Новый вектор свободных членовКурс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
17
18. СПОСОБЫ ПРИВЕДЕНИЯ СЛАУ К НОРМАЛЬНОМУ ВИДУ
→Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
18
19. СПОСОБЫ ПРИВЕДЕНИЯ СЛАУ К НОРМАЛЬНОМУ ВИДУ
Имея систему:Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
19
20. СПОСОБЫ ПРИВЕДЕНИЯ СЛАУ К НОРМАЛЬНОМУ ВИДУ
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
20
21. ПРИМЕРЫ ПРИВЕДЕНИЯ СЛАУ К НОРМАЛЬНОМУ ВИДУ
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
21
22. ПРИМЕРЫ ПРИВЕДЕНИЯ СЛАУ К НОРМАЛЬНОМУ ВИДУ
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
22
23. ПРИМЕРЫ ПРИВЕДЕНИЯ СЛАУ К НОРМАЛЬНОМУ ВИДУ
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
23
24. ПРИМЕРЫ ПРИВЕДЕНИЯ СЛАУ К НОРМАЛЬНОМУ ВИДУ
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
24
25. ПРИМЕРЫ ПРИВЕДЕНИЯ СЛАУ К НОРМАЛЬНОМУ ВИДУ
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
25
26. ПОСТРОЕНИЕ ИТЕРАЦИОННОГО ПРОЦЕССА МЕТОДОМ ПРОСТЫХ ИТЕРАЦИЙ
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
26
27. ПОСТРОЕНИЕ ИТЕРАЦИОННОГО ПРОЦЕССА МЕТОДОМ ПРОСТЫХ ИТЕРАЦИЙ
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
27
28. ПОСТРОЕНИЕ ИТЕРАЦИОННОГО ПРОЦЕССА МЕТОДОМ ПРОСТЫХ ИТЕРАЦИЙ
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
28
29. УСЛОВИЯ СХОДИМОСТИ ИТЕРАЦИОННОГО ПРОЦЕССА
Дана СЛАУ, приведенная кнормальному виду х=β+αх
Теорема 1. Пусть ||α||≤q<1. Тогда при
любом начальном векторе
МПИ сходится к единственному
решению х* и при всех
кєN справедливы оценки погрешности:
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
29
30. УСЛОВИЯ СХОДИМОСТИ ИТЕРАЦИОННОГО ПРОЦЕССА
Здесь обозначение ||.|| используется дляматричных и векторных норм,
согласованных между собой, т.е. таких, что
||Ax||≤||A||*||x||.
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
30
31. УСЛОВИЯ СХОДИМОСТИ ИТЕРАЦИОННОГО ПРОЦЕССА
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
31
32. УСЛОВИЯ СХОДИМОСТИ ИТЕРАЦИОННОГО ПРОЦЕССА
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
32
33. АПРИОРНАЯ И АПОСТЕРИОРНАЯ ОЦЕНКИ
Априорная оценка позволяетподсчитывать заранее число итераций k,
достаточное для получения решения х* с
заданной точностью ε при выбранном
начальном векторе
Наименьшее целое решение неравенства
относительно k
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
33
34. АПРИОРНАЯ И АПОСТЕРИОРНАЯ ОЦЕНКИ
Апостериорной оценкой пользуютсянепосредственно в процессе вычислений
и применяют для останова процесса
итераций при выполнении неравенства:
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
34
35. ПРИМЕР РЕШЕНИЯ МЕТОДОМ ПРОСТЫХ ИТЕРАЦИЙ
записать сходящийся процесс простых итераций. Засколько шагов этого процесса, начатого с нуль-вектора,
можно достичь точности ε=0,001 по норме-максимум?
Найти третье приближение, оценить его абсолютную
погрешность и сравнить ее с истинной погрешностью,
зная точное решение системы
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
35
36. ПРИМЕР РЕШЕНИЯ МЕТОДОМ ПРОСТЫХ ИТЕРАЦИЙ
Решение: Учитывая очевидную близость матрицыданной системы к единичной матрице, выделим
единицы из диагональных элементов, в результате чего
система преобразуется к виду:
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
36
37. ПРИМЕР РЕШЕНИЯ МЕТОДОМ ПРОСТЫХ ИТЕРАЦИЙ
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
37
38. ПРИМЕР РЕШЕНИЯ МЕТОДОМ ПРОСТЫХ ИТЕРАЦИЙ
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
38
39. ПРИМЕР РЕШЕНИЯ МЕТОДОМ ПРОСТЫХ ИТЕРАЦИЙ
Априорная оценка погрешностей:Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
39
40. ПРИМЕР РЕШЕНИЯ МЕТОДОМ ПРОСТЫХ ИТЕРАЦИЙ
При заданном векторе x(0)=0первым приближением
, служит
вектор β свободных членов;
следовательно
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
40
41. ПРИМЕР РЕШЕНИЯ МЕТОДОМ ПРОСТЫХ ИТЕРАЦИЙ
Требуемое количество шагов, достаточноедля достижения точности 0,001, может быть
найдено как первое из последовательности
натуральных чисел k, удовлетворяющих
неравенству:
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
41
42. ПРИМЕР РЕШЕНИЯ МЕТОДОМ ПРОСТЫХ ИТЕРАЦИЙ
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
42
43. ПРИМЕР РЕШЕНИЯ МЕТОДОМ ПРОСТЫХ ИТЕРАЦИЙ
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
43
44. ПРИМЕР РЕШЕНИЯ МЕТОДОМ ПРОСТЫХ ИТЕРАЦИЙ
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
44
45. ПРИМЕР РЕШЕНИЯ МЕТОДОМ ПРОСТЫХ ИТЕРАЦИЙ
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
45
46. МЕТОД ЗЕЙДЕЛЯ
Метод Зейделя - это такоевидоизменение МПИ(3) решения
СЛАУ, приведенных к виду (2), при
котором для подсчета i-й компоненты
(к+1)го приближения к искомому
вектору х* используется уже
найденные на этом, т.е. (к+1) шаге,
новые значения первых (i-1)
компонент.
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
46
47. МЕТОД ЗЕЙДЕЛЯ
-матрицакоэффициентов
-вектор свободных
членов
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
47
48. МЕТОД ЗЕЙДЕЛЯ
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
48
49. ПРИМЕР РЕШЕНИЯ МЕТОДОМ ЗЕЙДЕЛЯ
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
49
50. ПРИМЕР РЕШЕНИЯ МЕТОДОМ ЗЕЙДЕЛЯ
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
50
51. ПРИМЕР РЕШЕНИЯ МЕТОДОМ ЗЕЙДЕЛЯ
Начнем процесс итераций с того же начального приближенияпри к=0,1,2 последовательно получаем:
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
, далее
51
52. ПРИМЕР РЕШЕНИЯ МЕТОДОМ ЗЕЙДЕЛЯ
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
52
53. ПРИМЕР РЕШЕНИЯ МЕТОДОМ ЗЕЙДЕЛЯ
Курс «Вычислительная математика»Тема «Итерационные методы решения СЛАУ»
53
54. ПРЕИМУЩЕСТВА ИТЕРАЦИОННЫХ МЕТОДОВ
1.Если итерации сходятся достаточнобыстро, т.е. для решения системы
требуется менее k итераций, то
получаем выигрыш во времени, т.к.
число арифметических действий,
необходимых для одной итерации,
пропорционально n,а общее число
арифметических действий в методе
Гаусса пропорционально n.
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
54
55. ПРЕИМУЩЕСТВА ИТЕРАЦИОННЫХ МЕТОДОВ
2.Погрешности округлений в МПИсказываются значительно меньше, чем
в методе Гаусса. Кроме того, МПИ
является самоисправляющимся, т.е.
отдельные ошибки, допущенные в
вычислениях, не отражаются на
окончательном результате, т.к.
ошибочное приближение можно
рассматривать как новый начальный
вектор.
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
55
56. ПРЕИМУЩЕСТВА ИТЕРАЦИОННЫХ МЕТОДОВ
3.МПИ становится особенновыгодным для решения систем, у
которых значительное число
нулевых коэффициентов(при
решении уравнений в частных
производных).
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
56
57. ПРЕИМУЩЕСТВА ИТЕРАЦИОННЫХ МЕТОДОВ
4.Итерационные методы легкопрограммируются на ЭВМ.
Особенно метод Зейделя.
Курс «Вычислительная математика»
Тема «Итерационные методы решения СЛАУ»
57
58.
СПАСИБО ЗА ВНИМАНИЕ© ФГБОУ ВПО ИжГТУ имени М.Т. Калашникова, 2013
© Исенбаева Елена Насимьяновна, 2013
























































 Математика
Математика








