Прямые методы решения СЛАУ. Метод Гаусса

1.

Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ижевский государственный технический университет
имени М. Т. Калашникова»
Кафедра «АСОИУ»
Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод
Гаусса»
Автор Исенбаева Е.Н., старший преподаватель
Ижевск
2013

2. ПРЯМЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ(СЛАУ)

Прямые методы – методы,
приводящие к решению за
конечное число
арифметических операций.
Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
2

3. ПРЯМЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ(СЛАУ)

Операции реализуются
точно
решение точное
(точные методы)
Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
3

4. ПРЯМЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ(СЛАУ)

Возникают округления
результаты
приближенные
Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
4

5. ПРЯМЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ(СЛАУ)

Прямые методы:
–метод Крамера
–метод Гаусса
Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
5

6. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ

Решить систему линейных алгебраических
уравнений методом Гаусса.
Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
6

7. МЕТОД ГАУССА

Метод Гаусса - метод
последовательного исключения
неизвестных.
Метод имеет прямой и обратный
ход.
Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
7

8. ПРЯМОЙ ХОД МЕТОДА ГАУССА

Прямой ход состоит в исключении
элементов, расположенных ниже
элементов, соответствующих главной
диагонали матрицы А.
Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
8

9. ПРЯМОЙ ХОД МЕТОДА ГАУССА

Расчет элементов ведущей строки:
Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
9

10. ПРЯМОЙ ХОД МЕТОДА ГАУССА

Расчет элементов нижележащих строк:
Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
10

11. ОБРАТНЫЙ ХОД МЕТОДА ГАУССА

Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
11

12. АЛГОРИТМ МЕТОДА ГАУССА

Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
12

13. АЛГОРИТМ МЕТОДА ГАУССА

Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
13

14. МЕТОД ГАУССА С ПОСТОЛБЦОВЫМ ВЫБОРОМ ВЕДУЩЕГО ЭЛЕМЕНТА

Метод Гаусса с постолбцовым
выбором ведущего элемента модификация метода Гаусса, в которой на
каждом этапе прямого хода уравнения
обрабатываемой подсистемы
переставляют так, чтобы деление
производилось на наибольший по модулю
в данном столбце элемент.
Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
14

15. УТОЧНЕНИЕ КОРНЕЙ

Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
15

16. ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ МЕТОДОМ ГАУССА

Метод Гаусса
Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
16

17. ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ МЕТОДОМ ГАУССА

Метод Гаусса с постолбцовым
выбором ведущего элемента
Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
17

18. НАХОЖДЕНИЕ ОБРАТНОЙ МАТРИЦЫ

Обратная матрица- решение Х уравнения
АХ=Е
где Х есть:
Е есть:
Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
18

19. НАХОЖДЕНИЕ ОБРАТНОЙ МАТРИЦЫ

• Матричное уравнение АХ=В заменяем
эквивалентной системой. Получаем n
систем векторно-матричных уравнений:
Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
19

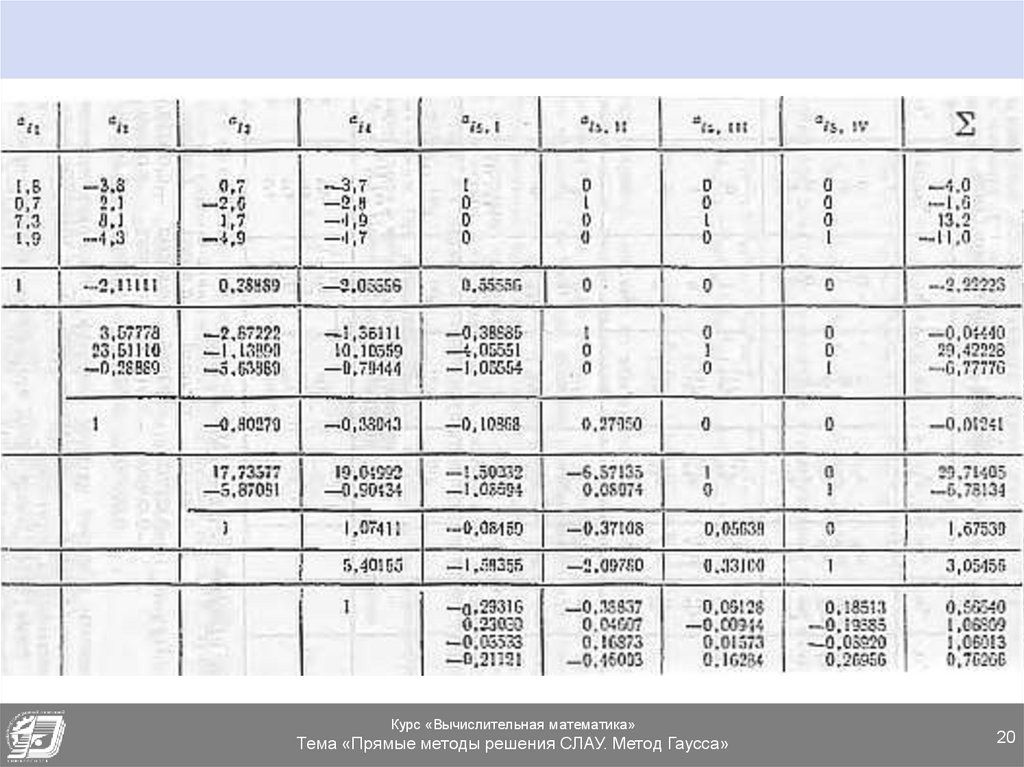
20.

Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
20

21. ОБРАТНАЯ МАТРИЦА.ПРИМЕР

Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
21

22. ОБРАТНАЯ МАТРИЦА. ПРИМЕР

Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
22

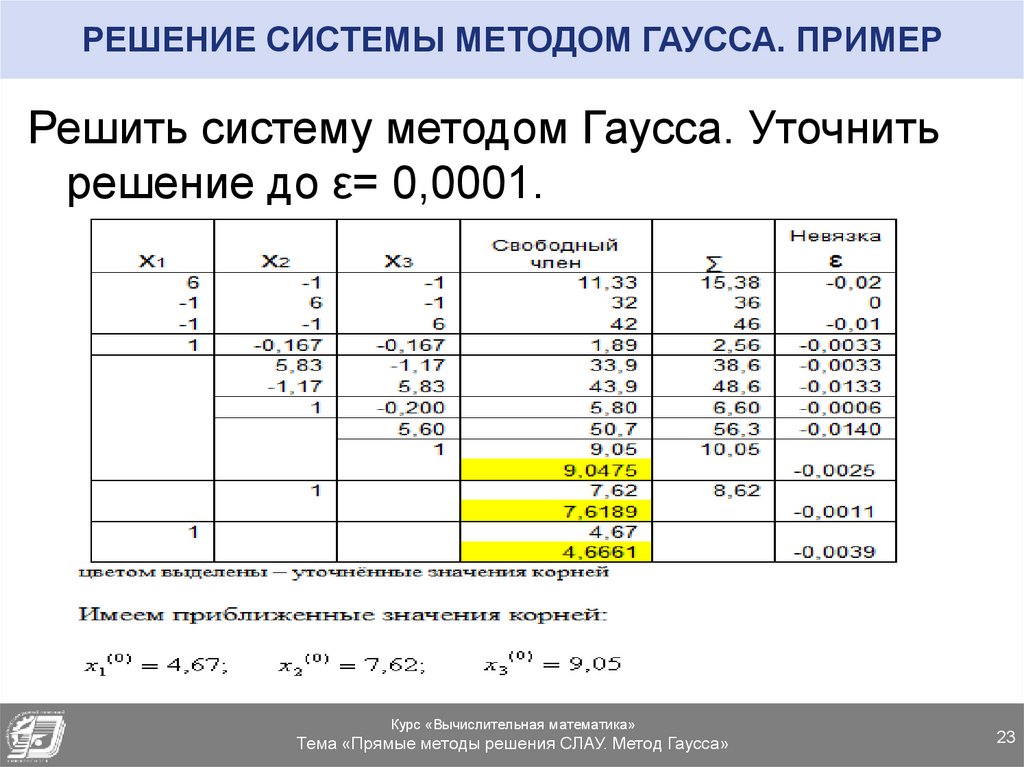
23. РЕШЕНИЕ СИСТЕМЫ МЕТОДОМ ГАУССА. ПРИМЕР

Решить систему методом Гаусса. Уточнить
решение до ε= 0,0001.
Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
23

24. РЕШЕНИЕ СИСТЕМЫ МЕТОДОМ ГАУССА. ПРИМЕР

Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
24

25. РЕШЕНИЕ СИСТЕМЫ МЕТОДОМ ГАУССА. ПРИМЕР

Курс «Вычислительная математика»
Тема «Прямые методы решения СЛАУ. Метод Гаусса»
25

26.

СПАСИБО ЗА ВНИМАНИЕ
© ФГБОУ ВПО ИжГТУ имени М.Т. Калашникова, 2013
© Исенбаева Елена Насимьяновна, 2013