Похожие презентации:
Полупроводник как активная среда
1. Курс «Квантовая электроника» ЧЕТВЕРТАЯ ЛЕКЦИЯ полупроводник как активная среда
Евгений Николаевич Поповн.с. лаб. «волоконная оптика и сенсорика»
Санкт-Петербургский политехнический университет Петра Великого 2015-2016
2.
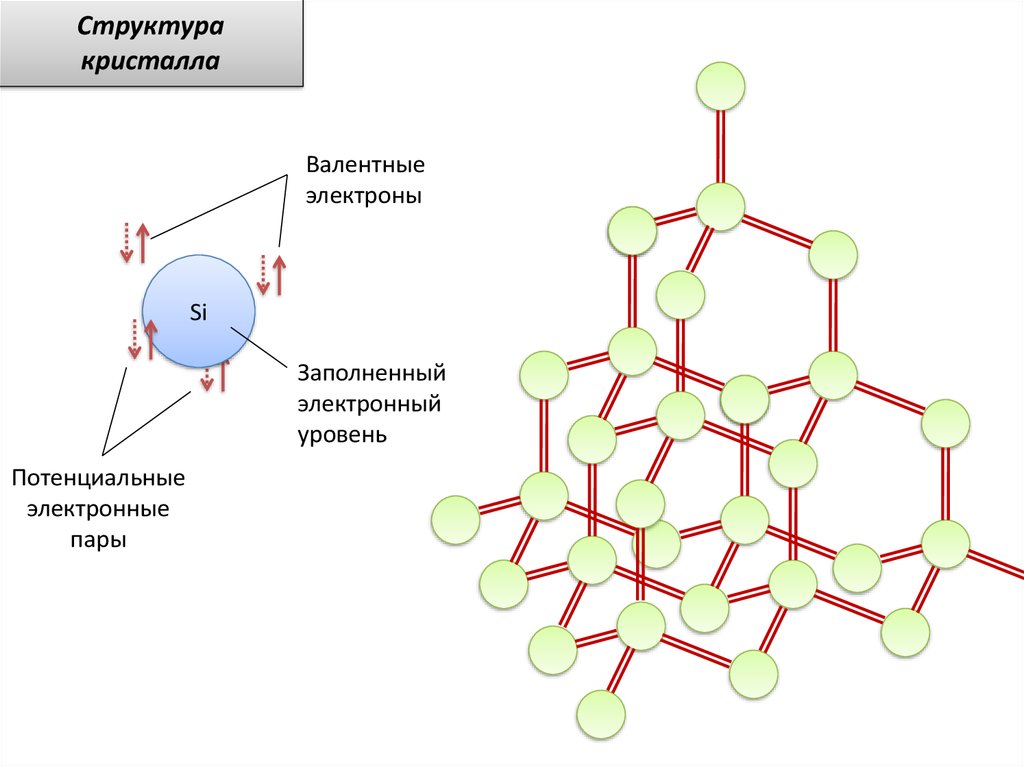
Структуракристалла
Валентные
электроны
Si
Заполненный
электронный
уровень
Потенциальные
электронные
пары
3.
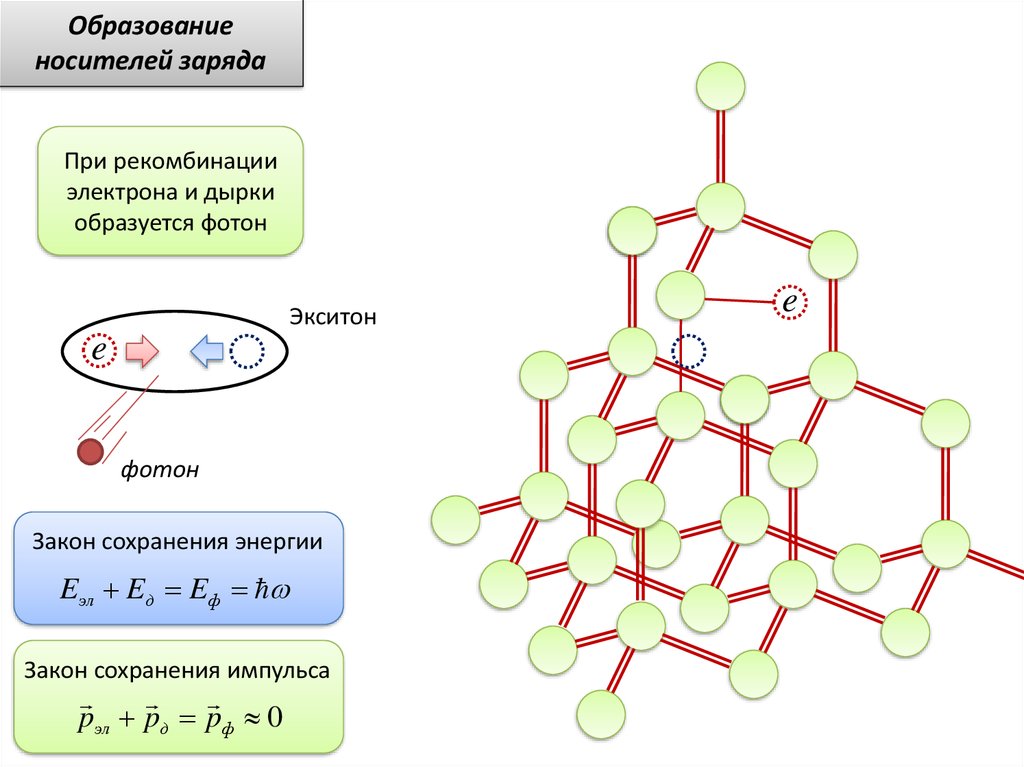
Образованиеносителей заряда
При рекомбинации
электрона и дырки
образуется фотон
Экситон
e
фотон
Закон сохранения энергии
Eэл Eд Eф
Закон сохранения импульса
pэл pд pф 0
e
4.
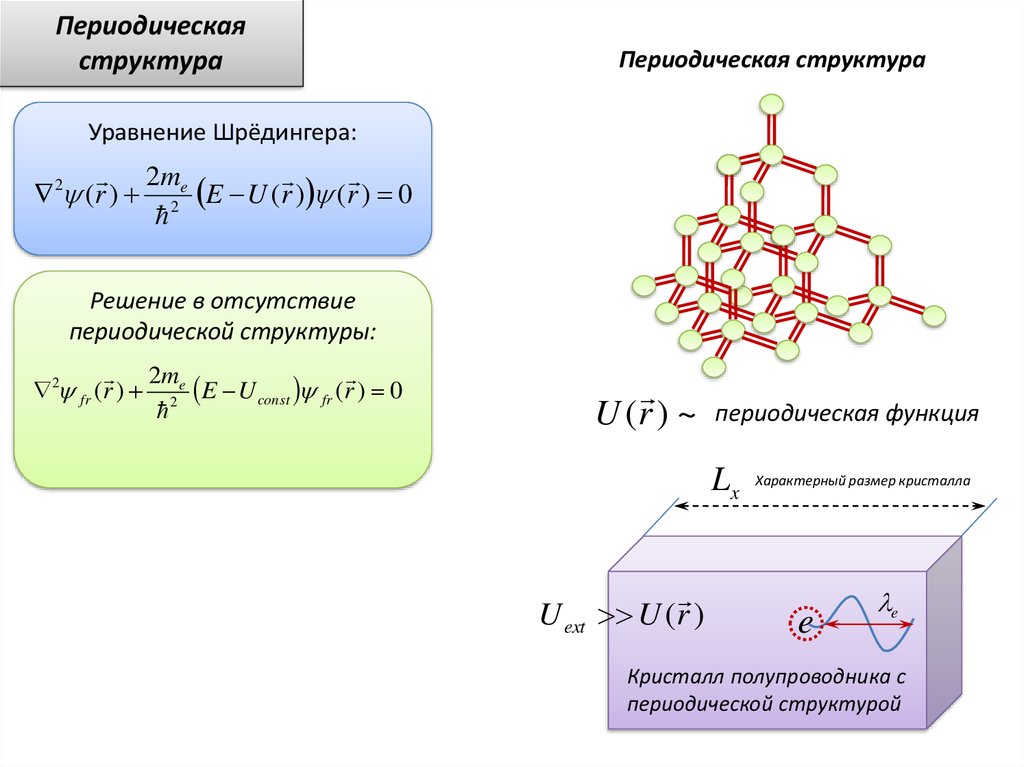
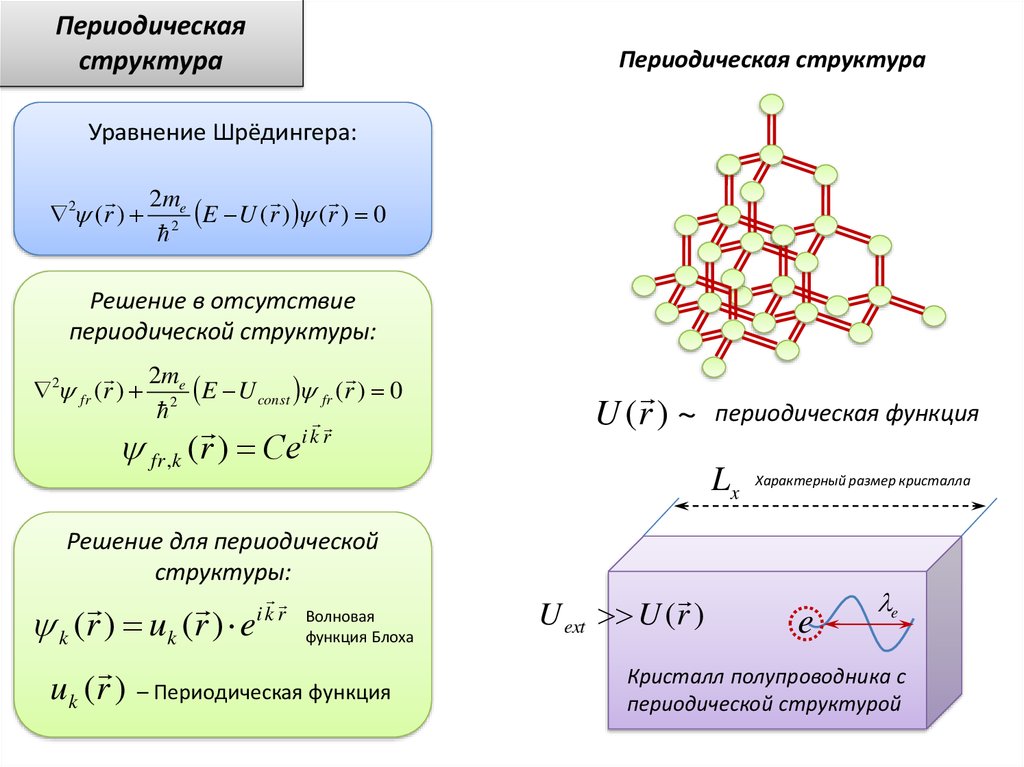
Периодическаяструктура
Периодическая структура
Уравнение Шрёдингера:
2m
2 (r ) 2 e E U (r ) (r ) 0
Решение в отсутствие
периодической структуры:
2m
2 fr (r ) 2 e E U const fr (r ) 0
U (r ) ~
периодическая функция
Lx
U ext U (r )
Характерный размер кристалла
e
e
Кристалл полупроводника с
периодической структурой
5.
Периодическаяструктура
Периодическая структура
Уравнение Шрёдингера:
2m
2 (r ) 2 e E U (r ) (r ) 0
Решение в отсутствие
периодической структуры:
2m
2 fr (r ) 2 e E U const fr (r ) 0
ik r
fr ,k (r ) Сe
Решение для периодической
структуры:
i k r Волновая
k (r ) uk (r ) e функция Блоха
u k (r ) – Периодическая функция
U (r ) ~
периодическая функция
Lx
U ext U (r )
Характерный размер кристалла
e
e
Кристалл полупроводника с
периодической структурой
6.
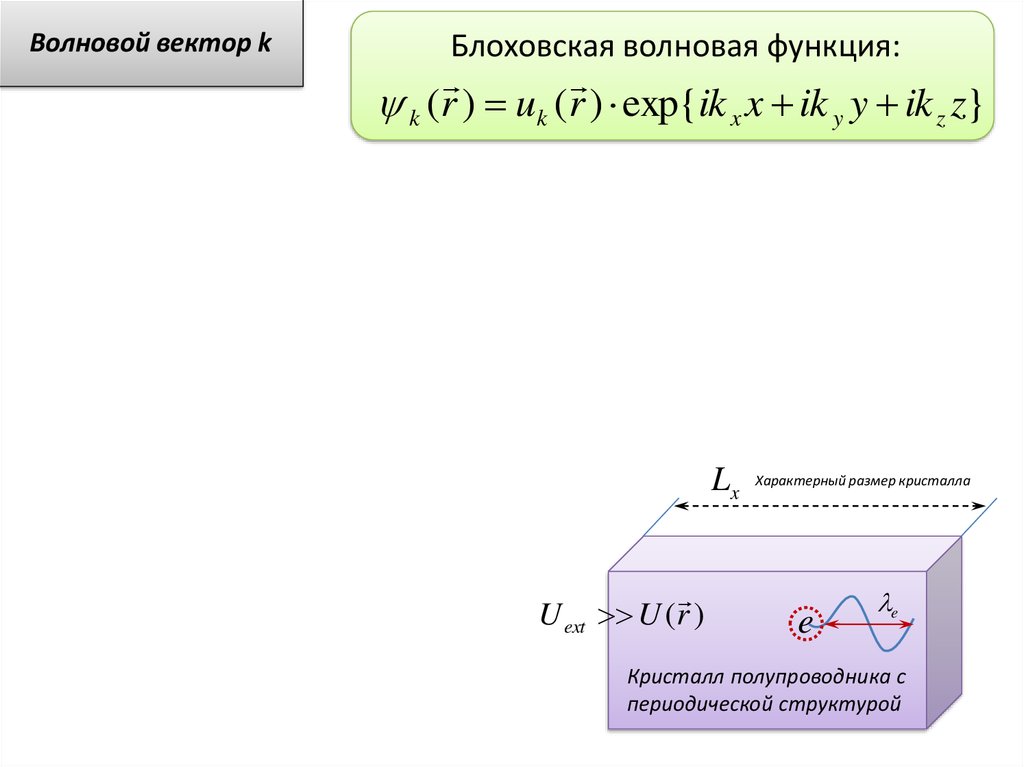
Волновой вектор kБлоховская волновая функция:
k (r ) uk (r ) exp{ik x x ik y y ik z z}
Lx
U ext U (r )
Характерный размер кристалла
e
e
Кристалл полупроводника с
периодической структурой
7.
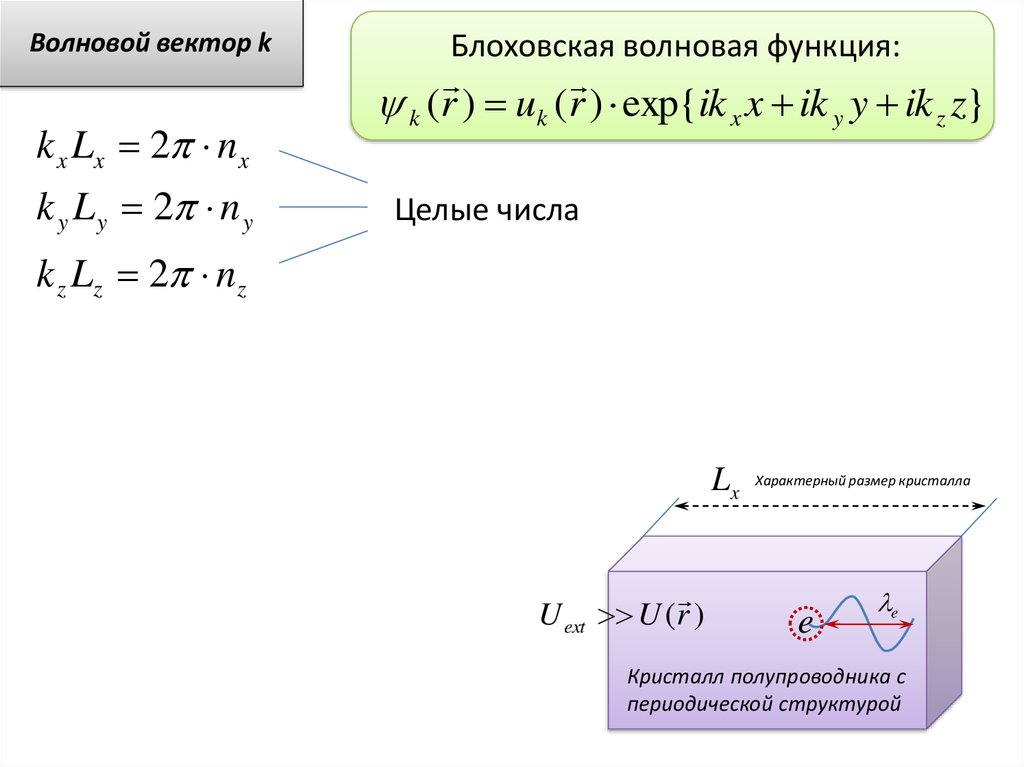
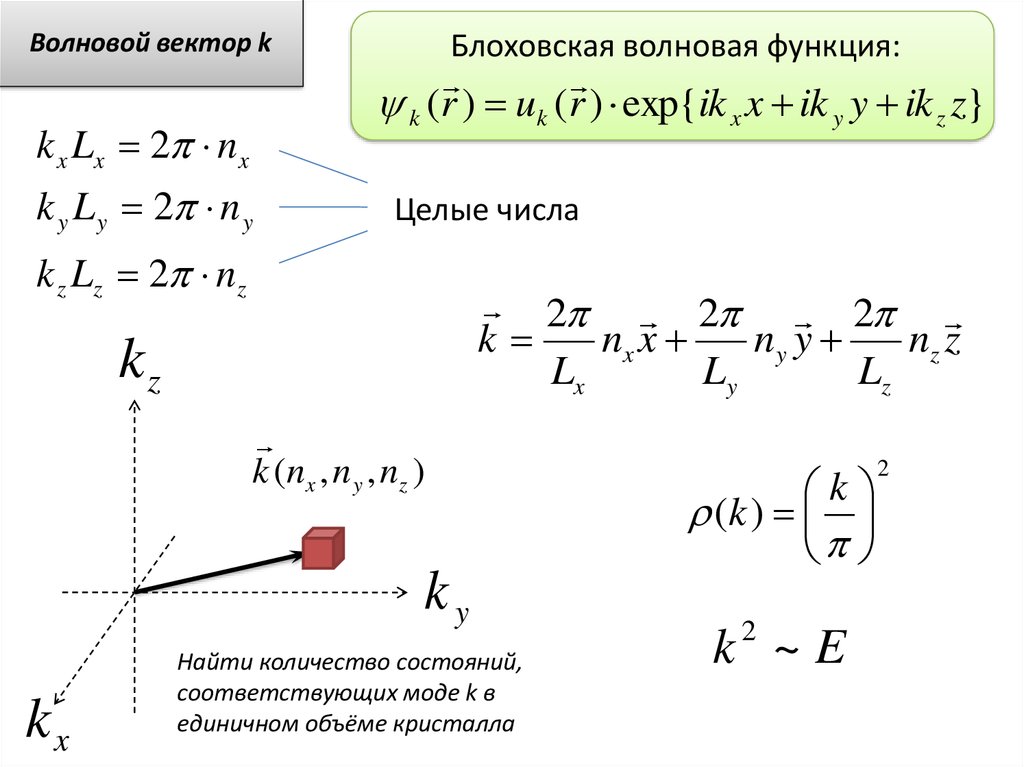
Волновой вектор kk x Lx 2 nx
k y L y 2 n y
Блоховская волновая функция:
k (r ) uk (r ) exp{ik x x ik y y ik z z}
Целые числа
k z Lz 2 nz
Lx
U ext U (r )
Характерный размер кристалла
e
e
Кристалл полупроводника с
периодической структурой
8.
Волновой вектор kk x Lx 2 nx
k y L y 2 n y
Блоховская волновая функция:
k (r ) uk (r ) exp{ik x x ik y y ik z z}
Целые числа
k z Lz 2 nz
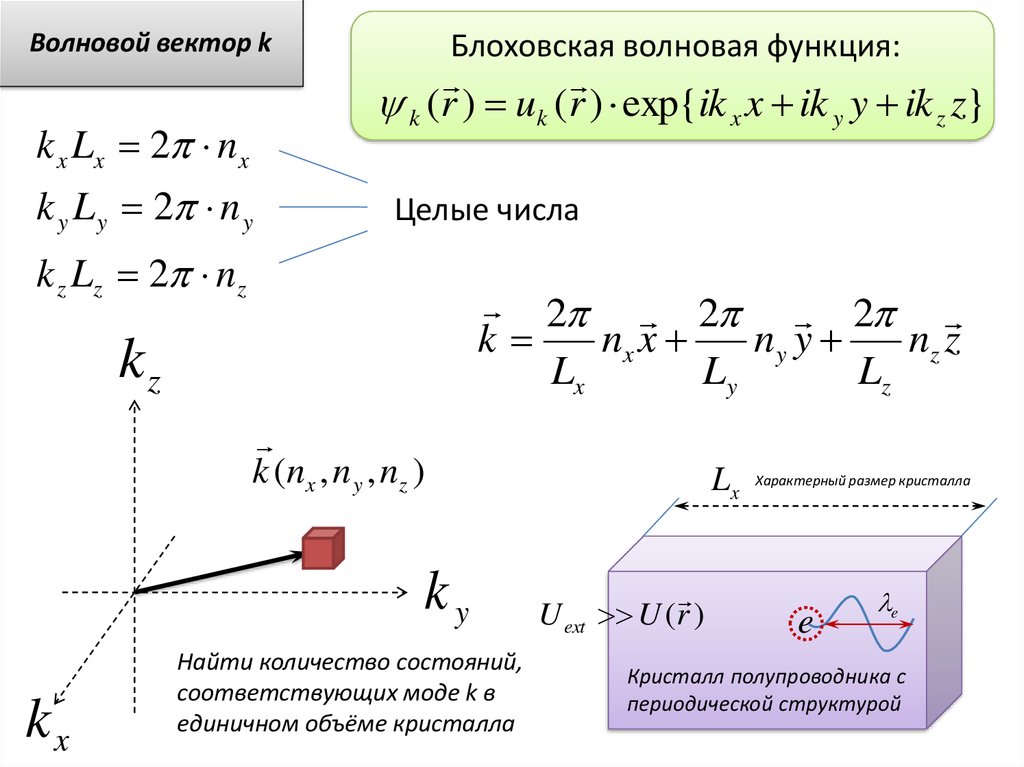
2 2 2
k
nx x
ny y
nz z
Lx
Ly
Lz
kz
k ( nx , n y , nz )
ky
kx
Найти количество состояний,
соответствующих моде k в
единичном объёме кристалла
Lx
U ext U (r )
Характерный размер кристалла
e
e
Кристалл полупроводника с
периодической структурой
9.
Волновой вектор kk x Lx 2 nx
k y L y 2 n y
Блоховская волновая функция:
k (r ) uk (r ) exp{ik x x ik y y ik z z}
Целые числа
k z Lz 2 nz
2 2 2
k
nx x
ny y
nz z
Lx
Ly
Lz
kz
k ( nx , n y , nz )
ky
kx
Найти количество состояний,
соответствующих моде k в
единичном объёме кристалла
k
(k )
2
k ~E
2
10.
Движение электронав полупроводнике
Периодическая структура
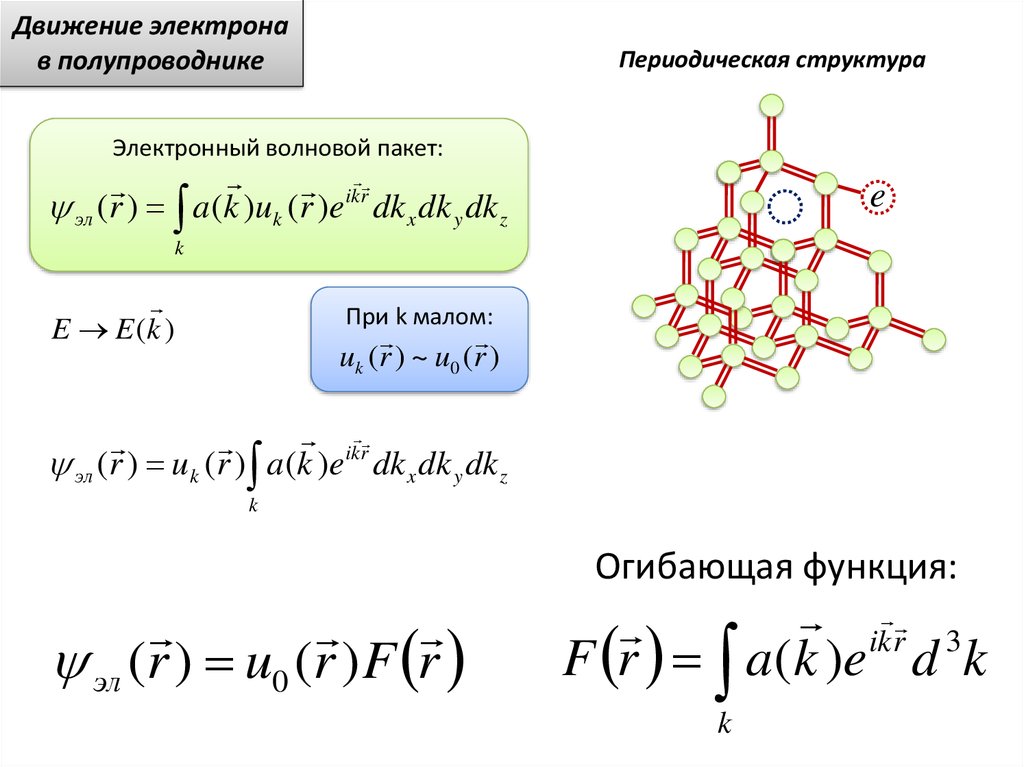
Электронный волновой пакет:
ik r
эл (r ) a(k )uk (r )e dk x dk y dk z
e
k
E E (k )
При k малом:
uk (r ) ~ u0 (r )
ik r
эл (r ) uk (r ) a(k )e dk x dk y dk z
k
Огибающая функция:
эл (r ) u0 (r ) F r
ik r 3
F r a(k )e d k
k
11.
Движение электронав полупроводнике
Периодическая структура
Электронный волновой пакет:
ik r
эл (r ) a(k )uk (r )e dk x dk y dk z
e
k
E E (k )
При k малом:
uk (r ) ~ u0 (r )
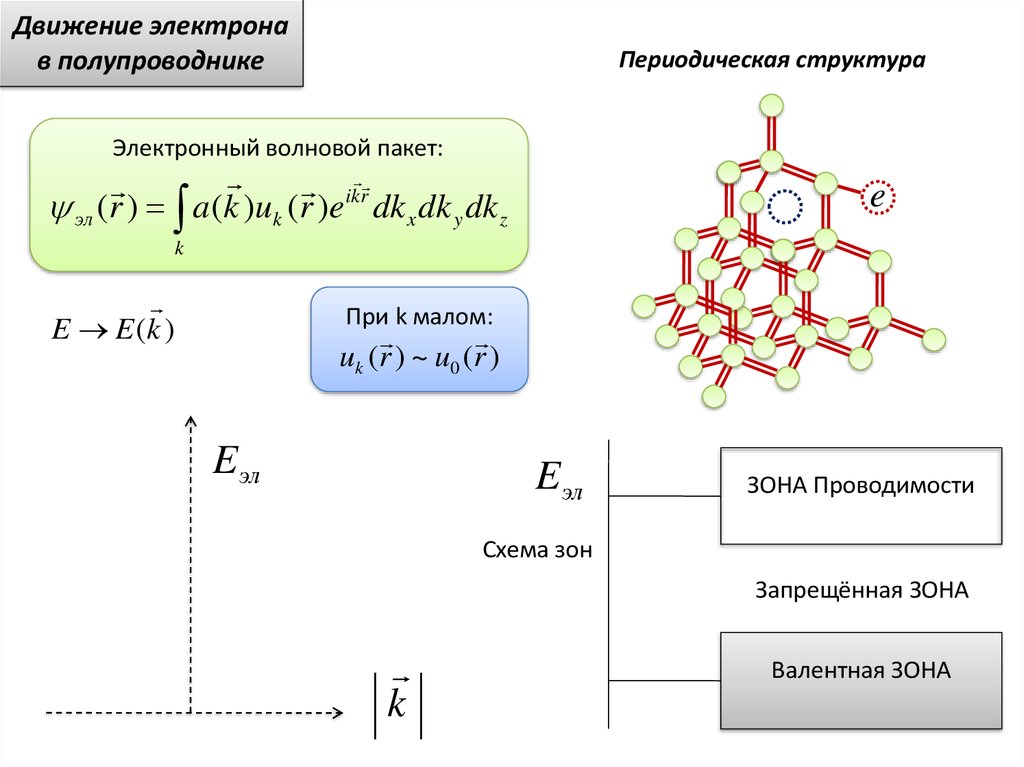
Eэл
Eэл
ЗОНА Проводимости
Схема зон
Запрещённая ЗОНА
k
Валентная ЗОНА
12.
Движение электронав полупроводнике
Периодическая структура
Электронный волновой пакет:
ik r
эл (r ) a(k )uk (r )e dk x dk y dk z
e
k
E E (k )
При k малом:
uk (r ) ~ u0 (r )
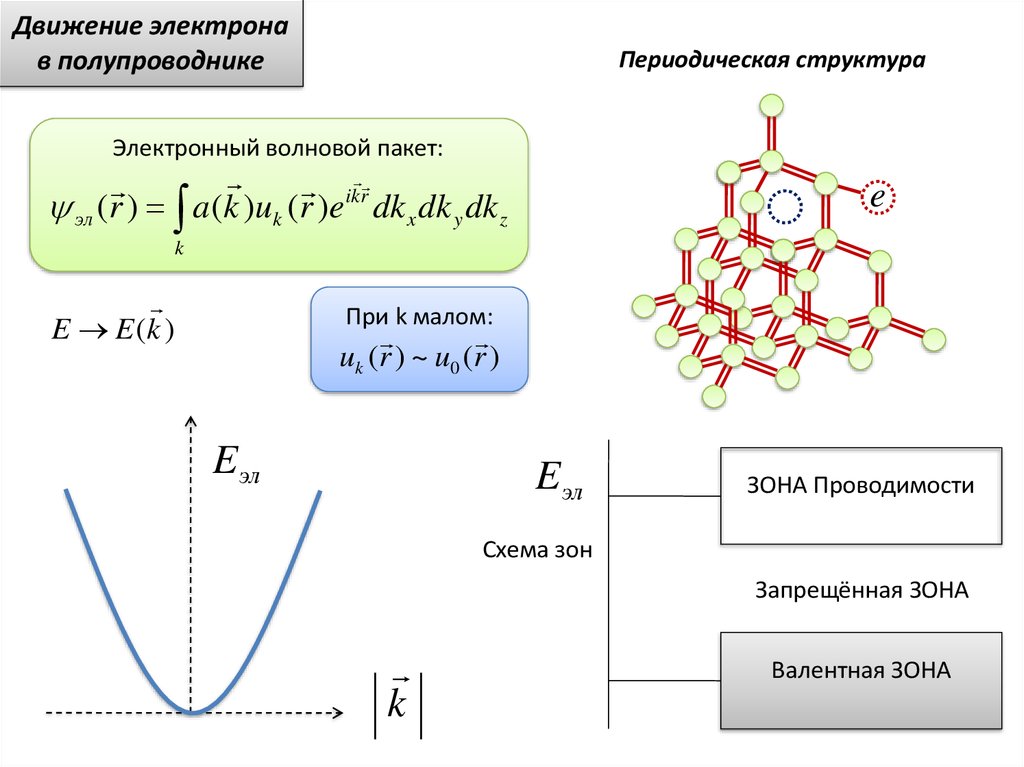
Eэл
Eэл
ЗОНА Проводимости
Схема зон
Запрещённая ЗОНА
k
Валентная ЗОНА
13.
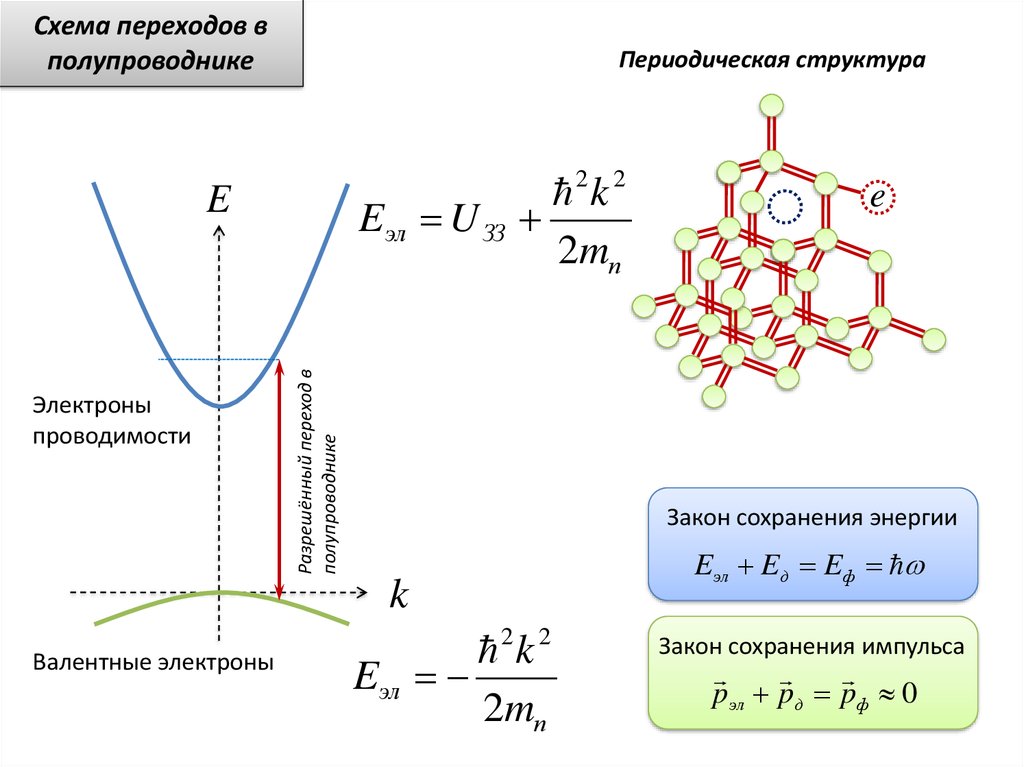
Схема переходов вполупроводнике
Периодическая структура
2
k
Eэл U ЗЗ
2mп
Разрешённый переход в
полупроводнике
E
Электроны
проводимости
e
Закон сохранения энергии
k
Валентные электроны
2
2k 2
Eэл
2mп
Eэл Eд Eф
Закон сохранения импульса
pэл pд pф 0
14.
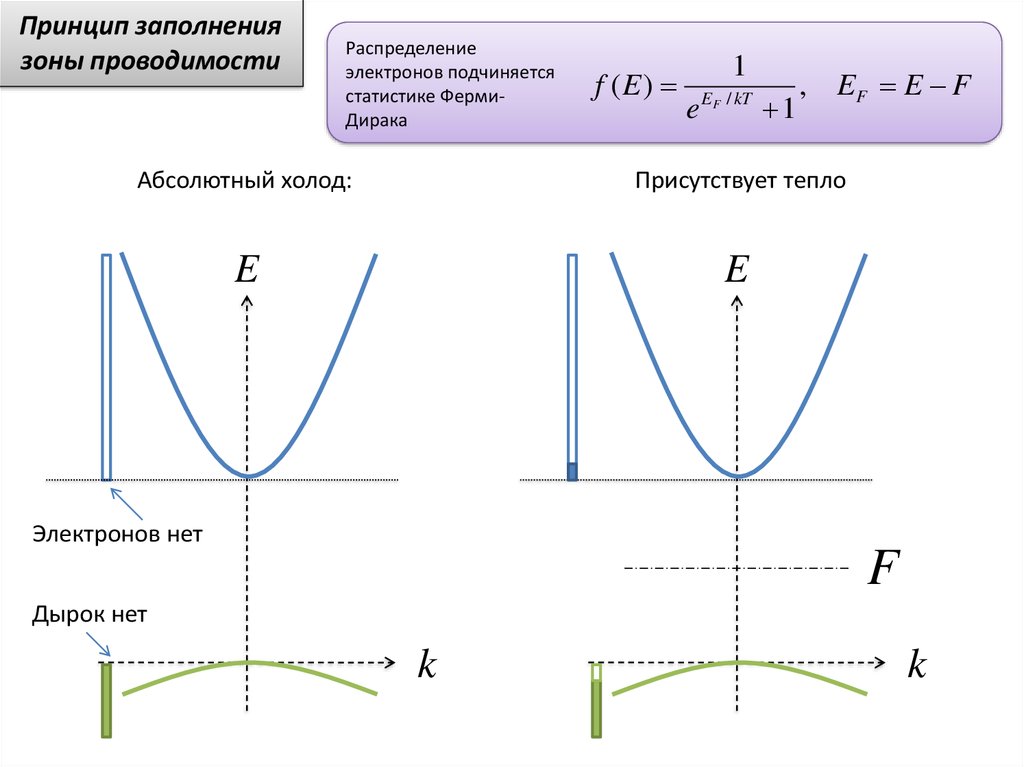
Принцип заполнениязоны проводимости
Распределение
электронов подчиняется
статистике ФермиДирака
f (E)
1
e
E F / kT
1
, EF E F
Абсолютный холод:
Присутствует тепло
E
E
Электронов нет
F
Дырок нет
k
k

 Физика
Физика