Обратные тригонометрические функции

1.

Обратные
ТРИГОНОМЕТРИЧЕСКИЕ
ФУНКЦИИ

2.

Под простейшими тригонометрическими уравнениями понимают уравнения вида:
sin x a
cos x a
где x – выражение с
переменной, a [1;1]
tgx a
где x – выражение с
переменной, a
любое число
28.03.24
ctgx a
Корнями являются arcsin, arccos, arctg, arcctg числа

3.

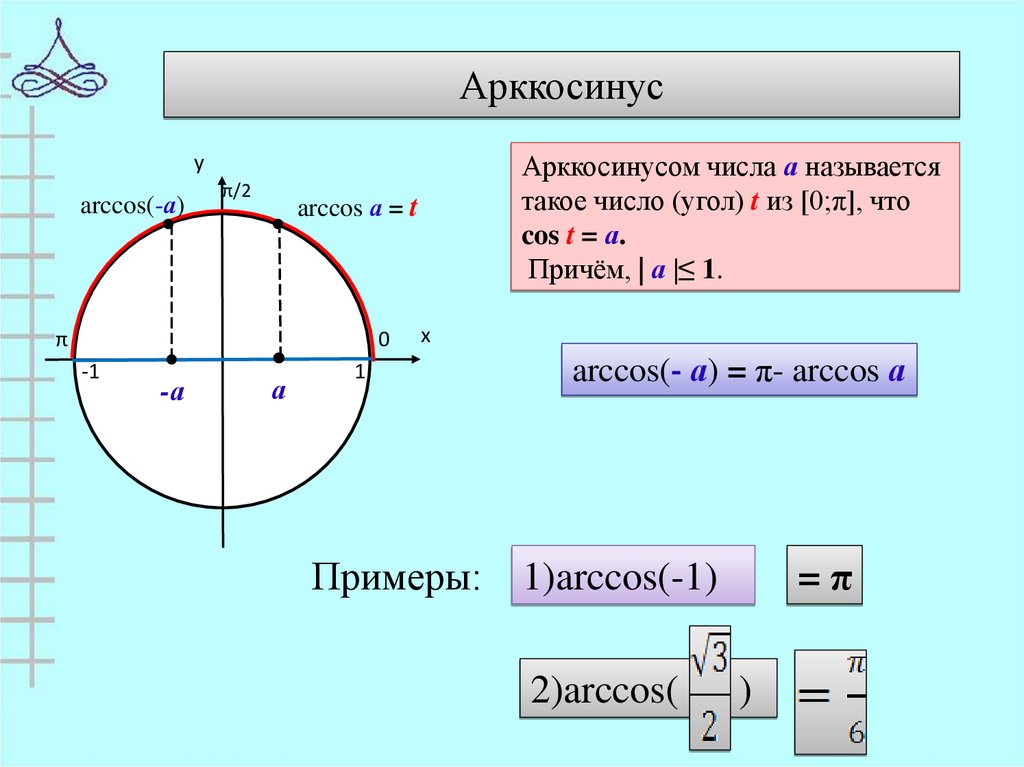
Арккосинус
Арккосинусом числа а называется
такое число (угол) t из [0;π], что
cos t = а.
Причём, | а |≤ 1.
у
arccos(-а)
π/2
arccos а = t
π
0
-1
-а
а
1
х
arccos(- а) = π- arccos а
Примеры: 1)arccos(-1)
2)arccos(
=π
)

4.

Таким образом, все корни в этом случае можно записать в виде совокупности:
arccos a 2 n, n Z;;
x
arccos a 2 k , k Z/.
1
2
arccos a 2 3
y
Масштаб :3
3
2
2
arccos a 0 arccos a
2
2
−1
Или, принято эти две записи объединять в одну:
x arccos a 2 m, m Z/.
28.03.24
2
arccos a 2
x

5.

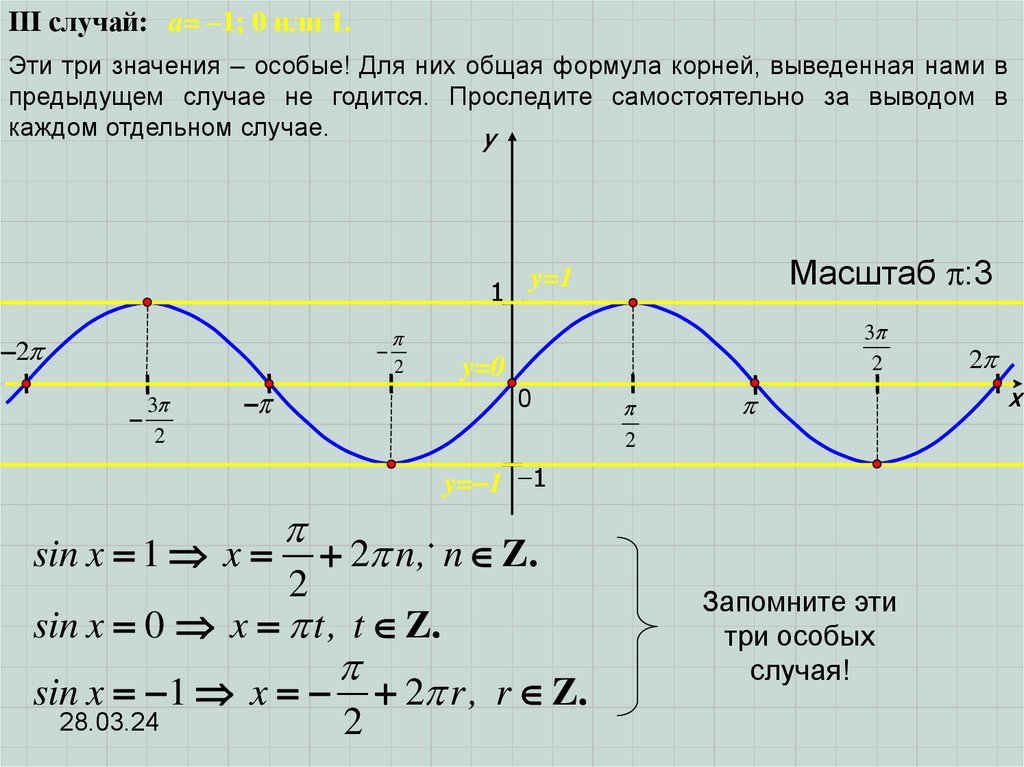
III случай: a= –1; 0 или 1.
Эти три значения – особые! Для них общая формула корней, выведенная нами в
предыдущем случае не годится. Проследите самостоятельно за выводом в
каждом отдельном случае.
y
Масштаб :3
1 y=1
2
2
y=0
3
2
0
3
2
2 x
2
y=–1 −1
cos x 1 x 2 n, n Z..
cos x 0 x
t, t Z..
2
cos x 1 x 2 r, r Z..
28.03.24
Запомните эти
три особых
случая!

6.

Арксинус
у
π/2
1
а
arcsin а =t
Арксинусом числа а называется
такое число (угол) t из [-π/2;π/2],
что sin t = а.
Причём, | а |≤ 1.
х
-а
-1
-π/2
Примеры:
arcsin(- а)
arcsin(- а)= - arcsin а

7.

Таким образом, все корни в этом случае можно записать в виде совокупности:
arcsin a ·2n, n Z;;
x
arcsin a · 2k 1 , k Z/.
y
Масштаб :3
1
3
2
2
arcsin a arcsin a
2
2
3
2
a
2
2
0 arcsin a arcsin a
2
−1
Или, принято эти две записи объединять в одну (подумайте, как это обосновать):
x 1 arcsin a m, m Z..
m
28.03.24
x

8.

III случай: a= –1; 0 или 1.
Эти три значения – особые! Для них общая формула корней, выведенная нами в
предыдущем случае не годится. Проследите самостоятельно за выводом в
каждом отдельном случае.
y
1
2
3
2
Масштаб :3
y=1
3
2
2
y=0
0
2
y=–1 −1
sin x 1 x
2 n, n Z..
2
sin x 0 x t, t Z..
sin x 1 x
28.03.24
2
2 r, r Z..
Запомните эти
три особых
случая!
2
x

9.

Арктангенс
а
у
Арктангенсом числа а называется
такое число (угол) t из (-π/2;π/2),
что tg t = а .
Причём, а Є R.
π/2
arctgа = t
0
х
arctg(-а )
arctg(-а) = - arctg а
-π/2
-а
1) arctg√3/3 = π/6
Примеры:
2) arctg(-1) =
-π/4

10.

Решение уравнения tgx=a исследуйте самостоятельно:
y
2
a
arc tga 2
3
2
2 4
arctga
1
0
−1
28.03.24
2
3
2
arctga
4
arctga
x a rc tga n, n Z/.
x
2

11.

Арккотангенс
у
-а
а
arcctg(- а)
arcctg а = t
π
0 х
Арккотангенсом числа а называется
такое число (угол) t из (0;π),
что ctg t = а.
Причём, а ЄR .
arcctg(- а) = π – arcctg а
Примеры:
1) arcctg(-1) = 3π/4
2) arcctg√3 = π/6

12.

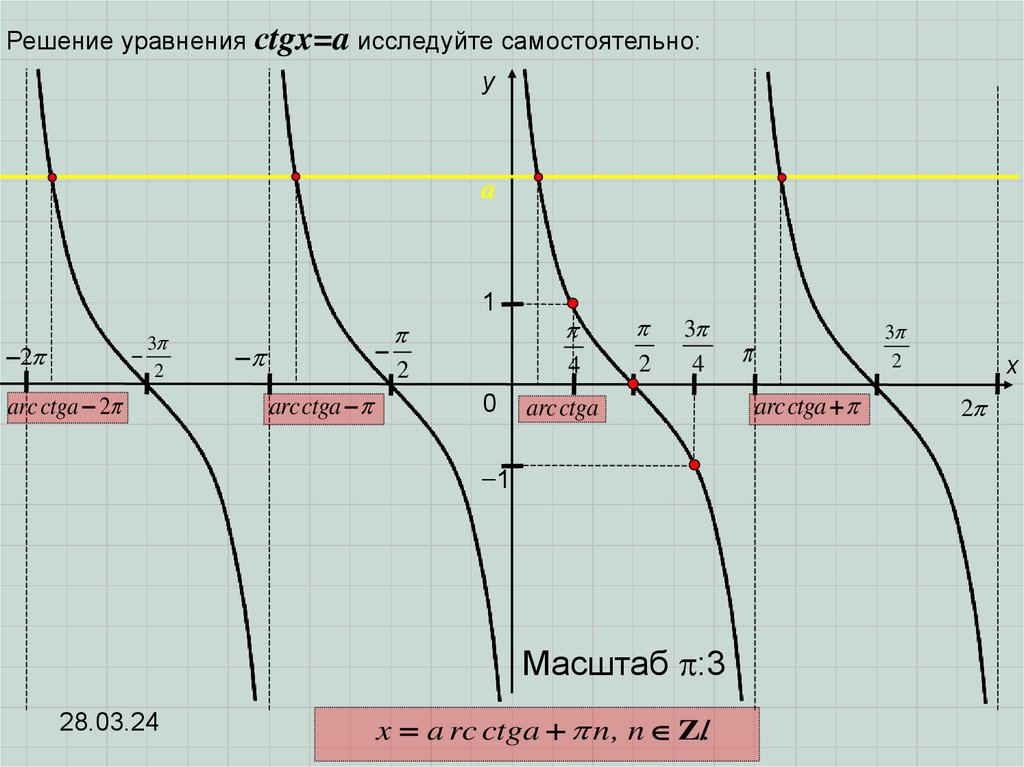
Решение уравнения сtgx=a исследуйте самостоятельно:
y
a
1
3
2
2
arc ctga 2
arcctga
2
0
4
2
3
4
arcctga
−1
Масштаб :3
28.03.24
x a rc ctga n, n Z/.
3
2
arcctga
x
2