Похожие презентации:
Геометрические решения тригонометрических задач
1.
Шишкина Елена Павловна,учитель математики МБОУ
г.Мурманска гимназии №2
2.
«АРИФМЕТИЧЕСКИЕ ЗНАКИ – ЭТОЗАПИСАННЫЕ ГЕОМЕТРИЧЕСКИЕ
ФИГУРЫ,
А
ГЕОМЕТРИЧЕСКИЕ
ФИГУРЫ – ЭТО НАРИСОВАННЫЕ
ФОРМУЛЫ.»
Д. ГИЛБЕРТ
3.
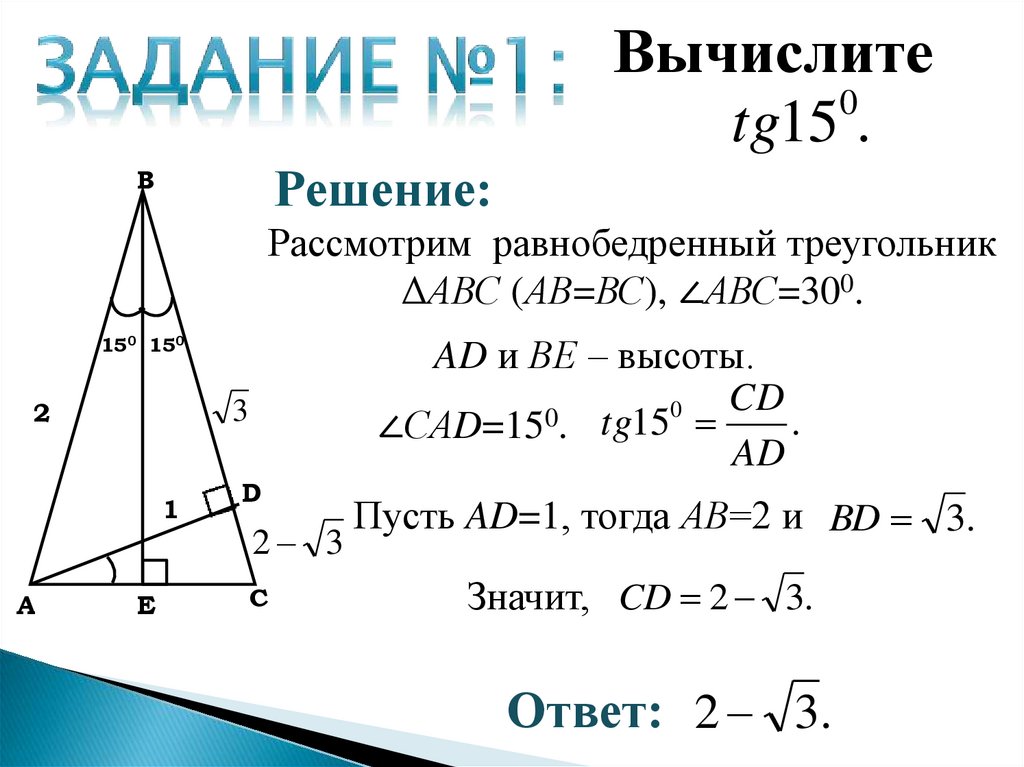
Вычислите0
tg15 .
Решение:
В
Рассмотрим равнобедренный треугольник
ΔАВС (АВ=ВС), ∠АВС=300.
AD и ВЕ – высоты.
CD
0
0
.
∠САD=15 . tg15
AD
150 150
2
3
1
А
E
D
2 3
С
Пусть AD=1, тогда АВ=2 и BD 3.
Значит, CD 2 3.
Ответ: 2 3.
4.
В450
2
Решение:
Рассмотрим равнобедренный треугольник
ΔАВС (АВ=ВС), ∠АВС=450.
1
Так как ∠ВСА=67030’, то ∠CAD=22030’.
CD
0
,
Пусть AD=1, tg 22 30
D
AD
1
А
Вычислите
0
tg 22 30 .
CD BC BD AB AD
С
2 AD 2 AD 2 1.
Ответ:
2 1.
5.
1Докажите тождество cos 36 cos 72
2
В
0
0
Доказательство:
Рассмотрим равнобедренный треугольник
ΔАВС (АВ=ВС), точку D (D∈BC и AD=BD=AC).
x
Пусть ∠АВС=х, тогда ∠BAD=x, ∠ADC=2x,
∠ACD=2x ∠DAC=x, ∠ADB=3x.
Суммы внутренних углов треугольников
ABD, ACD и АВС равны по 5х, т.е. х=360.
3x D
2x
x
x
А
2x
С
Итак, ∠АВС=360 и ∠ADC=720.
Так как D∈BC, то ВС=BD+DC.
Пусть BD=1, тогда АВ=2cos360 и CD=2cos720.
Так как АВ=ВС,
то 2cos360=1+2cos720.
1
Значит, cos 36 cos 72 .
2
0
0
6.
Докажите тождествоВ
3
sin 51
7
0
1
1
sin 77
7
1. Так как треугольники ABD, ADC и
ABC равнобедренные, то 7х=1800,
5x D
0
2x
т.е.
x
А
5
sin 25
7
0
1
Доказательство:
x
2x
1
5
x 25 .
7
3x
С
2.
BC = BD + DC.
0
7.
Пусть длина общей высоты, проведенной извершины А в треугольниках ABD, ADC и ABC,
равна 1 (H∈BC, AH⊥BC, AH=1), то:
AH
из ΔABH (AH⊥BH) BC AB
sin ABH
из ΔADH (AH⊥DH)
AH
BD AD
sin ADH
из ΔAСH (AH⊥СH)
AH
DC AC
sin ACH
Значит,
1
5
sin 25
7
0
1
3
sin 51
7
0
1
0
;
3
sin 51
7
1
0
;
1
sin 77
7
0
;
0
.
5
sin 25
7
1
1
1
sin 77
7
8.
Вычислитеsin 18
Решение:
В
В задаче 3 были определены величины углов с
вершинами в точках A, B, C и D.
ΔАВС ~ ΔCAD, так как оба они равнобедренные с общим
углом при основаниях (∠АСВ=∠ACD).
D
А
AC CD
, т.е. AC 2 AB CD.
AB AC
Если АС=а и АВ=b (a<b, так как ∠АВС=360 и ∠АСВ=720), то
CD=b-a и a2=b2-ab.
Это число называют золотым
a
5 1
сечением или числом Фидия (Фидий
.
Отсюда
b
2
– отец Архимеда).
Значит,
С
1 CD
1 AC 1 a
,
Так как sin 180 = cos 720, а cos 720 = 2
AC
2 AB 2 b
5 1
0
то sin 18 =
5 1
4
Ответ:
4
9.
Вычислитеctg10 4 cos10 .
В
Решение:
100
E
D
А
1
С
Рассмотрим прямоугольный треугольник
ΔАВС, в котором ∠АВС=100, ∠АСВ=900,
D∈BC, E∈AB и AD=DE=BE.
Пусть АС=1.
Определив величины углов, замечаем:
ВС= ctg100, BD=4cos100, CD=tg600.
Так как ВС=BD+DC, то
ctg100=4cos100+tg600.
Ответ:
3.
10.
Докажите, что sin2α=2 sinα cosαВ
Доказательство:
α
α
1
D
α
А
E
С
Рассмотрим равнобедренный
треугольник ΔАВС (АВ=ВС=1),
∠АВС=2α, AD и ВЕ – высоты.
По рисунку AD=sin 2α, AE=EC=sin α,
BE=cos α.
AB BE
,
Так как ΔABE ~ ΔCAD, то
AC AD
1
cos
т.е.
.
2 sin sin 2
Значит, sin2α=2 sinα cosα.
11.
Докажите, что 1 – cos2α = 2 sin2αВ
Доказательство:
α
α
1
D
α
E
С
AE=EC=sin α, BD=cos 2α, CD = 1-cos 2α
ΔABE ~ ΔCAD
1
sin
АВ AE
Тогда,
, т.е.
2sin 1 cos 2
АС CD
Значит, 1 – cos2α = 2 sin2α
12.
Докажите, чтоВ
α
sin(α+β) = sinαcosβ + cosαsinβ
Доказательство:
β
a
c
Рассмотрим ΔАВС, в котором BD⊥AC, ∠ABD=α,
∠CBD=β. Точка D – внутренняя точка отрезка АС,
так как по условию α и β – острые углы. Пусть
ВС=а, АС=b, АВ=с и BD=h.
h
А
D
1
ac sin( ),
2
S ABD S CBD .
S ABC
С
S ABC
1
1
1
ch sin c sin a cos ac sin cos .
2
2
2
1
1
1
S CBD ah sin a sin c cos ac cos sin .
2
2
2
Значит, sin( ) sin cos cos sin .
S ABD
13.
Каким должен бытьострый угол х, если
A
15 12 cos x 7 4 3 sin x 4
Решение:
D
2 3
C
AC 2 3, CD 3, CB 2.
3
x
Рассмотрим рисунок
Тогда AD 15 12 cos x и BD 7 4 3 sin x
2
B
по теореме косинусов,
а АВ=4 по теореме Пифагора.
Значит, D∈AB.
14.
A1
Так как ΔАВС прямоугольный и sin A , то А 30 .
2
По теореме косинусов из ΔACD следует, что
CD2 AC 2 AD2 2 AC AD cos 30 ,
т.е. 3 12 y 2 6 y,
2 3
x
3
D
где буквой у обозначена длина стороны AD.
Имеем y 2 6 y 9 0, y 3.
C
2
B
Итак, AD 3. Так как 32 ( 3 ) 2 (2 3 ) 2 ,
то в Δ ACD ∠ADC=900.
Тогда x=600.
Ответ: 600.
15.
Вычислите arctg 1 + arctg 2 + arctg 3.B
Решение:
C
M
A
N
arctg 3 = ∠BAM,
arctg 2 = ∠CAN,
arctg 1 = ∠BAC
(∠BAC – острый угол
прямоугольного равнобедренного
треугольника АВС).
Итак, arctg 1 + arctg 2 + arctg 3 = π.
16.
Вычислите2
arctg arcctg 5.
3
В
Решение:
D
С
2
arctg CAD,
3
arcctg 5 BAD,
BAC 45 .
2
arctg arcctg 5
3
4
A
.
Ответ:
4
17.
ВычислитеB
cos(arcctg3+arctg0,5).
Решение:
D
C
ctg ∠DAB=3 и tg ∠DAC=0,5.
ΔАВС – равнобедренный,
∠АВС=900.
Значит, arcctg 3 arctg 0,5 ,
4
2
cos(arcctg 3 arctg 0,5)
2.
M
A
N
2
Ответ:
.
2
18.
ВычислитеB
D
2
1
tg arcsin
arccos
.
5
10
Решение:
2
2
0, то можно считать, что arcsin
C Так как
5
5
- это угол прямоугольного треугольника, у
которого отношение катетов равно 1 : 2. Тогда
величину этого угла можно рассматривать как
arctg 2. Аналогично рассуждая, получим
arccos
M
A
1
arctg 3.
10
Далее, по рисунку ∠МАВ=arctg3 и ∠NAC=arctg 2,
N
а их сумма равна .
4
Итак,
2
1
tg arcsin
arccos
tg 1.
4
5
10
19.
«Покаалгебра
и
геометрия
развивались врозь, их прогресс
был
медленным,
применение
–
ограниченным; когда же эти две
науки
стали
были
соединены,
помогать
друг
они
другу
и
быстро шагать к совершенству».
Ж.Л. Лагранж


















 Математика
Математика








