Касательная к окружности. Решение задач (8 класс)

1. «Касательная к окружности. Решение задач»

«КАСАТЕЛЬНАЯ К
ОКРУЖНОСТИ.
РЕШЕНИЕ ЗАДАЧ»
8 класс

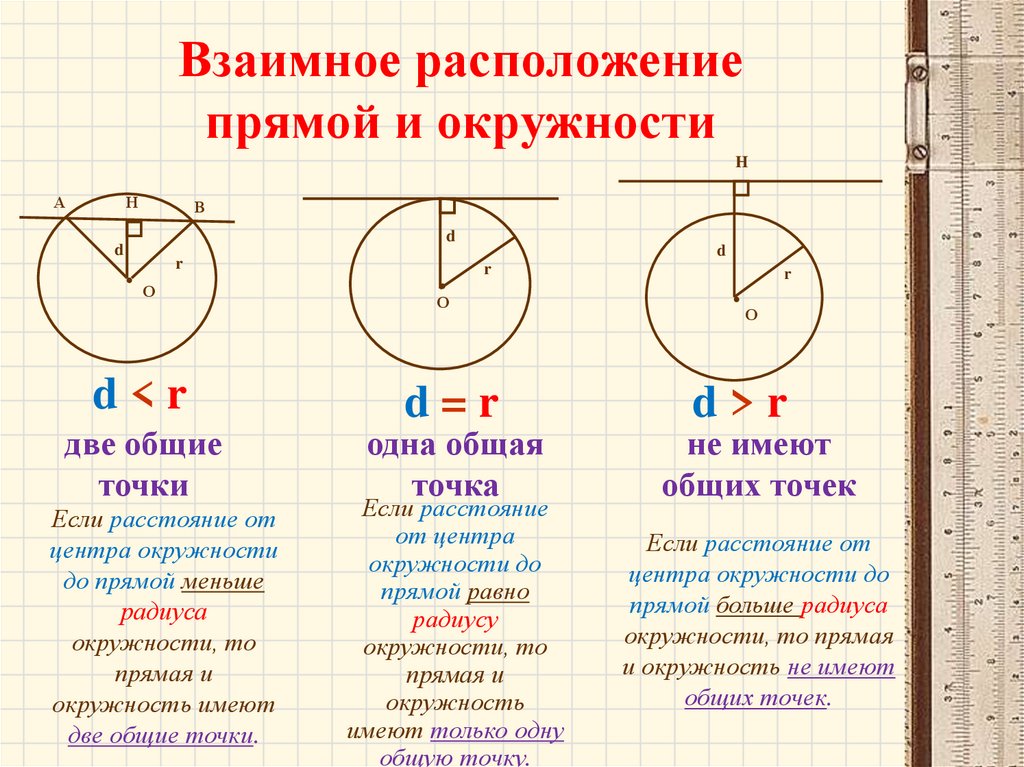
2. Взаимное расположение прямой и окружности

H
А
Н
В
d
d
r
О
d<r
две общие
точки
Если расстояние от
центра окружности
до прямой меньше
радиуса
окружности, то
прямая и
окружность имеют
две общие точки.
d
r
О
d=r
одна общая
точка
Если расстояние
от центра
окружности до
прямой равно
радиусу
окружности, то
прямая и
окружность
имеют только одну
общую точку.
r
О
d>r
не имеют
общих точек
Если расстояние от
центра окружности до
прямой больше радиуса
окружности, то прямая
и окружность не имеют
общих точек.

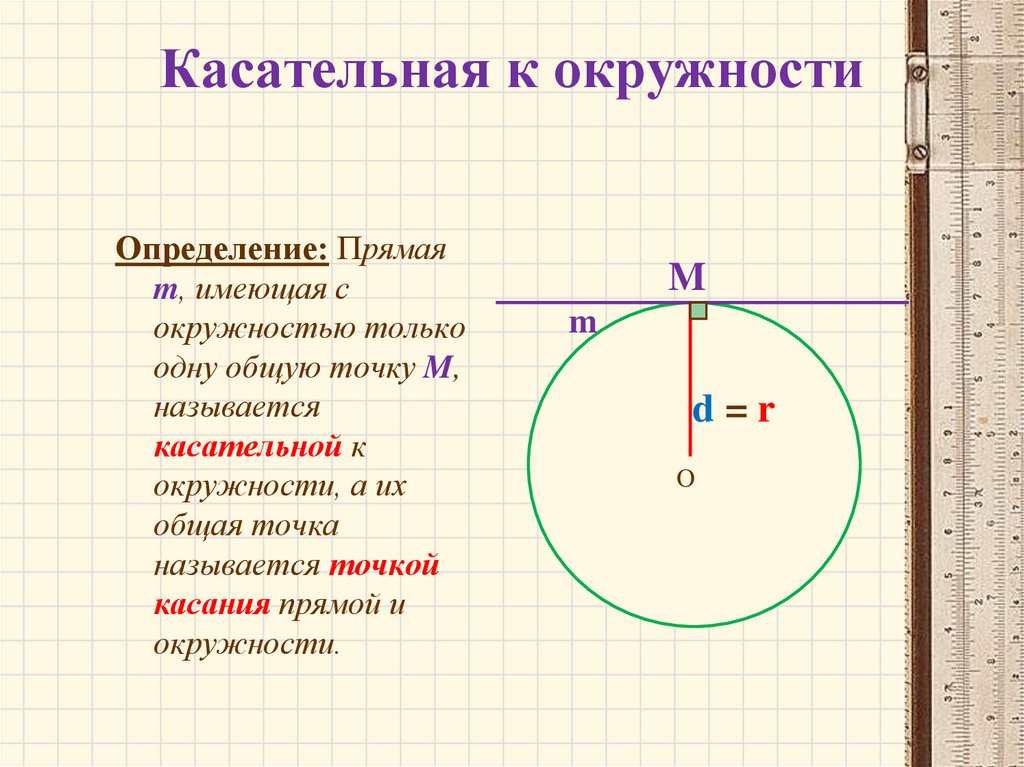
3. Касательная к окружности

Определение: Прямая
m, имеющая с
окружностью только
одну общую точку M,
называется
касательной к
окружности, а их
общая точка
называется точкой
касания прямой и
окружности.
M
m
d=r
O

4. Свойство касательной: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

m – касательная к
окружности с
центром О
М – точка касания
OM=r - радиус
m OM
M
m
O

5. Свойство касательных, проходящих через одну точку:

▼ По свойству касательной
Отрезки касательных к
1 90o , 2 90o.
окружности, проведенные
из одной точки, равны и
∆АВО, ∆АСО–прямоугольные
составляют равные углы
∆АВО=∆АСО–по гипотенузе
с прямой, проходящей через
эту точку и центр окружности. и катету:
В
1
О
3
4
2
С
А
ОА – общая,
ОВ=ОС – радиусы
АВ=АС
и
3 4
▲

6. Признак касательной: Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна радиусу, то она

является касательной.
M
окружность с центром О
m
радиуса OM
m – прямая, которая проходит
через точку М
и
m OM
m – касательная
O

7. № 639

Дано: окружность, <BOA = 60,
r = 12 см
Найти: АВ
Решение:
AOB прямоуголь ный, А 90 0 О 30 0
1
OB OA OA 24см.
2
Т .Пифогора :
АВ 2 ОА 2 ОВ 2
АВ 2 24 2 12 2 576 144 432
АВ 432 144 3 12 3
Ответ : 12 3

8. Решение задач на готовых чертежах:

РЕШЕНИЕ ЗАДАЧ НА ГОТОВЫХ
ЧЕРТЕЖАХ:
1)
Дано: R=5, AB – касательная.
Найти: OB.
Решение:
AOB прямоугольный, AO AB 5;
OB AO 2 AB 2 50 5 2 .

9.

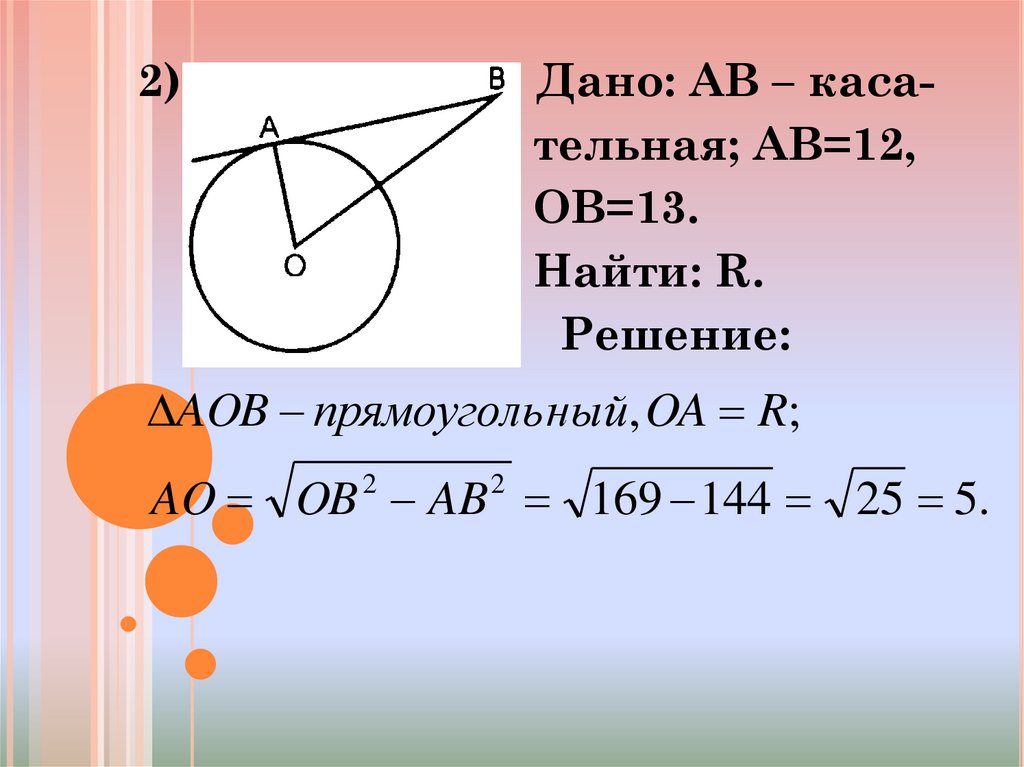
2)
Дано: AB – касательная; AB=12,
OB=13.
Найти: R.
Решение:
AOB прямоуголь ный, OA R;
AO OB AB 169 144 25 5.
2
2

10.

3)
Дано: AB, АC – касательные, OB=2, AO=4.
Найти: BOC .
Решение:
1
AOB прямоуголь ный, OB AO
2
0
0
BAO 30 , BOA 60 AOC ,
BOC 60 60 120 .
0
0
0

11.

4)
Дано: AB – касательная, R=6, AO=
=OB.
Найти: AO.
Решение:
AOB равнобедренный, OH высота, биссектриса,
медиана, радиус; OH 6; AH HB 8;
AOH прямоуголь ный AO OH 2 AH 2 64 36 10.

12.

Решить задачи по учебнику
К каждой задаче выполнить рисунок, на рисунке
отметить все, что известно по условию задачи,
записать «дано», «найти», «решение»
№ 638;
№ 640;
№ 642.
Решение задач записать в тетрадь и
отправить учителю в личное сообщение