Среднее арифметическое числового набора

1.

СРЕДНЕЕ
АРИФМЕТИЧЕСКОЕ
ЧИСЛОВОГО
НАБОРА

2.

Числовой набор в статистике — это последовательность
чисел, неупорядоченная, конечная.
Среднее арифметическое — число, равное отношению суммы
всех чисел числового набора к их количеству.
Среднее арифметическое даёт представление о центре данного
набора чисел. Иначе эту точку равновесия можно назвать центр масс.
Главное свойство среднего арифметического — зависимость от всех
чисел набора. Таким образом, в каком месте набора ни стояло бы число,
оно одинаково будет влиять на значение среднего арифметического.

3.

Как найти среднее арифметическое
приведённого набора чисел?
Представить это можно в виде дроби
3+4+5+2+3+4+4+2 =
+5+3
3,5
10
В приведённом
примере 5 оценок оказались выше значения
среднего арифметического, и 5 — ниже. То есть оно
действительно располагается посередине набора и может дать
представление о его составе. Однако так бывает далеко не
всегда, наличие в числовом наборе слишком больших или
слишком малых относительно остальных чисел набора может
дать не очень корректное представление о всём наборе.

4.

Найди среднее арифметическое
числового набора.
6; 3; 7; 2; 3; 6; 6; 3; 9.

5.

Вычисли среднее арифметическое
числового набора. Округли его до целых.
6,7; 9,77; 3; 8,359; −1,1; 0,48; −7; −1.

6.

Температура воздуха в 2023 году при
измерении её в 12 часов дня представлена
в таблице.
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь
−9
−6
−5
−3
9
20
26
23
20
6
−1
−11
Найди среднюю температуру весной, ответ
округли до десятых.

7.

В наборе 10 чисел. Их среднее
арифметическое
составляет 26. Чему станет
равно среднее арифметическое,
если к одному из чисел набора
прибавить 10?

8.

МЕДИАНА

9.

Медиана — серединное значение числового набора,
упорядоченного по возрастанию. То есть такое число
набора, которое не больше ровно половины его элементов
и не меньше тоже ровно половины.
Медианный представитель — число из набора, наиболее
близкое по значению к медиане набора.
Упорядоченный числовой набор называется вариационным
рядом.

10.

Чтобы найти медиану числового набора, содержащего
нечётное количество чисел, нужно упорядочить их по
возрастанию, а затем найти число, находящееся ровно
посередине.
Чтобы найти медиану числового набора, содержащего
чётное количество чисел, нужно упорядочить их по
возрастанию, затем найти два числа, находящихся в
середине, и найти их среднее арифметическое, или
полусумму.
Пример:
Дан набор чисел: 1, 11, 6, 3. Сначала упорядочим его по
возрастанию и получим 1, 3, 6, 11. Заметим, что количество
чисел в наборе чётно. Воспользуемся правилом, возьмём числа,
расположенные посередине, это 3 и 6. Найдём их полусумму,
(3+6):2=4,5, и в соответствии с правилом это число и будет
медианой числового ряда.

11.

Медиана чаще всего близка или равна среднему
арифметическому числового набора. Однако так бывает
не всегда. Если в числовом наборе есть выбросы — резко
отличающиеся от всего набора значения — то медиана и
среднее арифметическое могут сильно различаться.
Таким образом, медиана устойчива относительно
выбросов в отличие от среднего арифметического и
может дать более точное представление о числовом
наборе, чем среднее арифметическое.

12.

Если опираться буквально на определение медианы, то
получится, что нужно двигаться по вариационному ряду с
двух сторон, и добраться до его середины.
Например, дан числовой набор:
4; 44; 8; 36, 82; 13; 35; 17,7 ;25 ;27 ,09.
Сначала нужно упорядочить числа по возрастанию, причём
располагать равные числа рядом. Затем после упорядочения
числового набора можно поочерёдно зачёркивать числа в
начале и в конце, так мы придём к середине.
Чему равна медиана?

13.

МОДА В
СТАТИСТИКЕ

14.

Мода — это значение, которое встречается в наборе
данных чаще всего. В отличие от среднего
арифметического мода может быть использована для
любых типов данных, включая категориальные и
номинальные
данные.
Чтобы найти моду, нужно подсчитать, сколько раз
каждое значение встречается в наборе данных, и
выбрать значение с наибольшим количеством
вхождений. Если два или более значений встречаются
одинаковое количество раз и чаще, чем любое другое
значение, то все они считаются модами, и набор
данных называется мультимодальным.

15.

Дан числовой набор:
3,
-5,
9,
8,
-5,
8,
-2,
2,
4,
-5
Чтобы найти моду подсчитываем, сколько раз каждое
число встречается в наборе. В этом случае, число -5
встречается три раза, что больше, чем любое другое
число. Таким образом, мода этого набора данных
равна -5.

16.

Ограничения моды
Как и среднее арифметическое, мода имеет свои
ограничения. Она не учитывает все значения в наборе
данных и может быть менее полезна, если данные
имеют несколько мод или если они равномерно
распределены.

17.

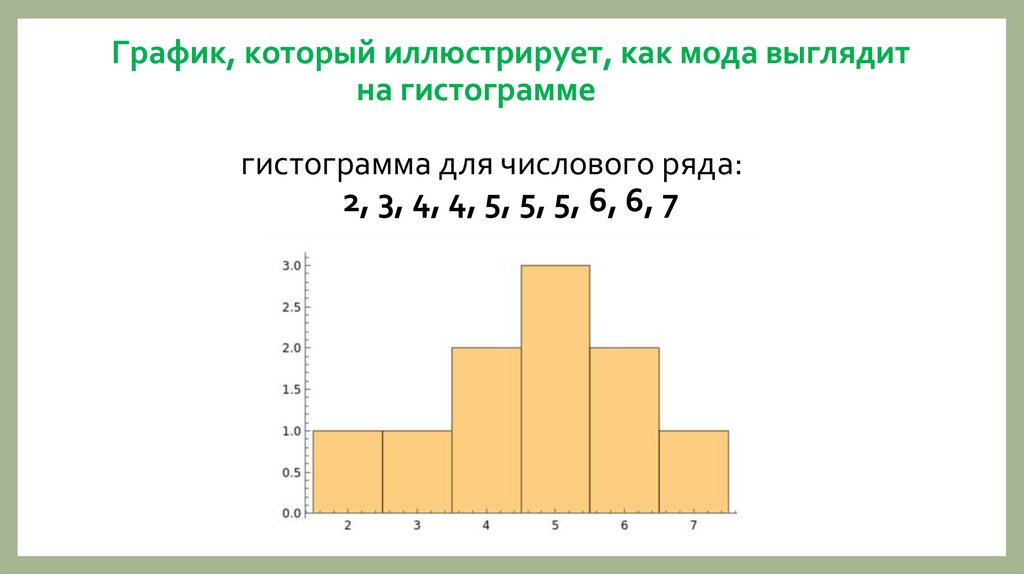
График, который иллюстрирует, как мода выглядит
на гистограмме
гистограмма для числового ряда:
2, 3, 4, 4, 5, 5, 5, 6, 6, 7

18.

ЧАСТОТА
ЗНАЧЕНИЙ В
МАССИВЕ ДАННЫХ

19.

Характеристика,
определяющая,
как
часто
повторяется та или иная величина, называется
частотой возникновения события, или кратко —
частота.
Частота — это число повторений какой-либо
величины параметра, то есть сколько раз за какой-то
период происходило некоторое событие.

20.

Пример.
Сколько учеников в возрасте 12 лет?
Сколько учеников 13 лет?
Сколько учеников 11 лет?
v
v
v
Сумма частот всегда должна равняться общему количеству
элементов в выборке.

21.

Виды частот.
Частоты бывают двух видов — абсолютные и
относительные.
Абсолютная частота определяет, как часто определённое
событие происходит в данном эксперименте.
Относительная частота — это отношение абсолютной
частоты к общему количеству, представленное в
процентах.

22.

Найдём относительную частоту
Найдём сумму всех относительных частот.
0,6 + 0,3 + 0,1 = 1.
Свойство относительных частот гласит о том, что их сумма в каждом
случае должна быть равна единице. А если в расчёте на проценты, то
100 %.

23.

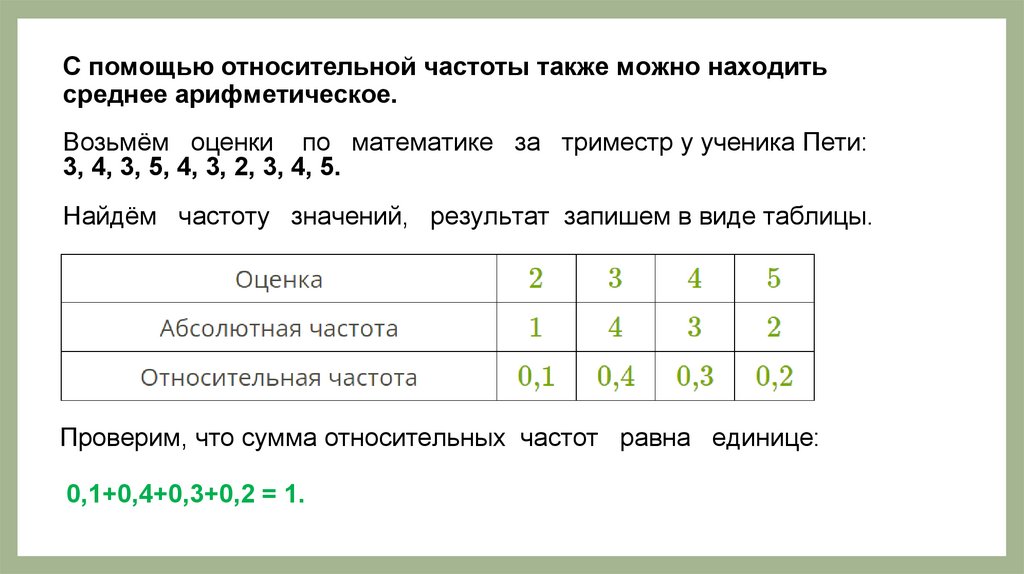
С помощью относительной частоты также можно находить
среднее арифметическое.
Возьмём оценки по математике за триместр у ученика Пети:
3, 4, 3, 5, 4, 3, 2, 3, 4, 5.
Найдём частоту значений, результат запишем в виде таблицы.
Проверим, что сумма относительных частот равна единице:
0,1+0,4+0,3+0,2 = 1.

24.

Чтобы найти среднее арифметическое, оценки умножим на их
относительные частоты и сложим получившиеся произведения.
2⋅0,1+3⋅0,4+4⋅0,3+5⋅0,2 = 3,6.
За триместр Петя получит оценку 4, так как 3,6 ≈ 4.
Это правило можно проверить, если посчитать среднее арифметическое
привычным способом.

25.

Задача 1.
Дан ряд чисел:
10, 15, 10, 11, 10, 10, 18, 11, 10, 11, 11, 11, 10, 23, 11,
11.
Найдите частоту всех значений этого ряда
Задача 2.
В 7 «В» классе на уроке физкультуры измеряли рост
учащихся. Выяснилось, что в классе всего пять различных
групп. Результаты записали в виде таблицы.
Сколько всего учеников в классе?

26.

Задача 3.
Чему равны относительные частоты значений в наборе, где 10
различных значений, но каждое встречается...
1)
2)
Ровно 6 раз
Ровно 4 раз

27.

Задача 4.
Сёме захотелось выяснить, как часто он встречает людей с одинаковыми
именами.
1. Сколько знакомых в итоге насчитал Сёма?
2. 2. Посчитай и соотнеси относительную частоту встречи каждого имени. (При
вычислениях округли частоту до сотых.)
3. Саша ? Артём ? Максим? Федя ? Гоша? Серёжа?

28.

5. Дан числовой набор 5, 4, 8, 1, 1, 3, 4, 65, 8, 1. Найдите абсолютную
и относительную частоту.
6. Дана последовательность букв:
Ф А В Ы Д О В Л Ы Д Я Ю Ф Л Ч Л И О Ы Д С О Ы Ж Ф.
Найдите в этой последовательности частоту:
букв Д, Ы, Ф, С.
7. В числовом наборе 5 значений. Частоты четырёх значений
известны: 0.35, 0.2, 0.1, 0.05. Найдите частоту пятого значения.
8. Пусть число m является медианой числового набора. Покажите, что
сумма частот всех чисел набора, которые не больше m, не меньше
чем 0,5.

29.

ВЫБОРКА. ТИПЫ
ВЫБОРОК.

30.

Генеральная совокупность
Суммарная численность объектов наблюдения (люди,
домохозяйства, предприятия, населенные пункты и т.д.),
обладающих определенным набором признаков (пол,
возраст, доход, численность, оборот и т.д.), ограниченная
в пространстве и времени.
• Все жители Москвы (10,6 млн. человек по данным переписи
2002 года)
• Мужчины-Москвичи (4,9 млн. человек по данным переписи
2002 года)
• Юридические лица России (2,2 млн. на начало 2005 года)
• Розничные торговые точки, осуществляющие продажу
продуктов питания (20 тысяч на начало 2008 года) и т.д.

31.

Выборка (Выборочная совокупность)
Свойство выборки корректно отражать генеральную
совокупность. Одна и та же выборка может быть
репрезентативной и нерепрезентативной для разных
генеральных совокупностей.
Пример:
• Выборка, целиком состоящая из москвичей, владеющих
автомобилем, не репрезентирует все население Москвы.
• Выборка из российских предприятий численностью до 100
человек не репрезентирует все предприятия России.
• Выборка из москвичей, совершающих покупки на рынке, не
репрезентирует покупательское поведение всех москвичей.

32.

Ошибка выборки (доверительный интервал)
Отклонение результатов, полученных с помощью выборочного
наблюдения от истинных данных генеральной совокупности.
Ошибка выборки бывает двух видов – статистическая и
систематическая. Статистическая ошибка зависит от размера
выборки. Чем больше размер выборки, тем она ниже.
Пример:
• Для простой случайной выборки размером 400 единиц максимальная
статистическая ошибка (с 95% доверительной вероятностью)
составляет 5%, для выборки в 600 единиц – 4%, для выборки в 1100 единиц
– 3% Обычно, когда говорят об ошибке выборки, подразумевают именно
статистическую ошибку.
• Систематическая ошибка зависит от различных факторов, оказывающих
постоянное воздействие на исследование и смещающих результаты
исследования в определенную сторону.

33.

Выборки делятся на два типа:
• вероятностные
• невероятностные
Вероятностные:
1.1 Случайная выборка (простой случайный отбор)
1.2 Механическая (систематическая) выборка
Разновидность случайной выборки, упорядоченная по
какому-либо признаку (алфавитный порядок, номер
телефона, дата рождения и т.д.).
Первый элемент отбирается случайно, затем, с шагом ‘n’
отбирается каждый ‘k’-ый элемент. Размер генеральной
совокупности, при этом – N=n*k

34.

1.3 Стратифицированная (районированная)
Применяется в случае неоднородности генеральной
совокупности. Генеральная совокупность разбивается на
группы (страты). В каждой страте отбор осуществляется
случайным или механическим образом.
1.4 Серийная (гнездовая или кластерная) выборка
При серийной выборке единицами отбора выступают не
сами объекты, а группы (кластеры или гнёзда). Группы
отбираются случайным образом. Объекты внутри групп
обследуются сплошняком.

35.

Невероятностные:
Отбор в такой выборке осуществляется не по принципам
случайности, а по субъективным критериям – доступности,
типичности, равного представительства и т.д.
2.1. Квотная выборка
Изначально выделяется некоторое количество групп объектов
(например, мужчины в возрасте 20-30 лет, 31-45 лет и 46-60 лет;
лица с доходом до 30 тысяч рублей, с доходом от 30 до 60 тысяч
рублей и с доходом свыше 60 тысяч рублей) Для каждой группы
задается
количество объектов,
которые
должны
быть
обследованы. Количество объектов, которые должны попасть в
каждую из групп, задается, чаще всего, либо пропорционально
заранее известной доле группы в генеральной совокупности, либо
одинаковым для каждой группы. Внутри групп объекты
отбираются произвольно. Квотные выборки используются в
маркетинговых исследованиях достаточно часто.

36.

2.2. Метод снежного кома.
Выборка
формируется
с
участием
самих
объектов
исследования. Метод часто применяется, когда необходимо
найти и опросить труднодоступные группы (например, людей,
имеющих высокий доход, людей, принадлежащих к одной
профессиональной группе, людей, имеющих какие-либо схожие
хобби/увлечения и т.д.)
2.3. Стихийная выборка
Размер и состав стихийных выборок заранее не известен, и
определяется только одним параметром – активностью
респондентов.
Пример - стихийных выборок – опросы в газетах/журналах,
анкеты,
отданные
респондентам
на
самозаполнение,
большинство интернет-опросов.

37.

2.4. Выборка типичных случаев
Отбираются единицы генеральной совокупности, обладающие
средним (типичным) значением признака. При этом возникает
проблема выбора признака и определения его типичного
значения.

38.

СЛУЧАЙНАЯ
ИЗМЕНЧИВОСТЬ

39.

Случайная изменчивость — это неустойчивость
величины, связанная с действием случайных факторов
или причин, часть из которых может быть неизвестна.
Пример.
Рост человека - самый простой и распространённый
пример. Невозможно без измерения определить рост
незнакомого нам человека, поэтому данная величина
для исследователя будет являться случайной. Но если
взять определённую выборку людей, также
незнакомых, и измерить их рост, то можно будет
отследить определённую закономерность.

40.

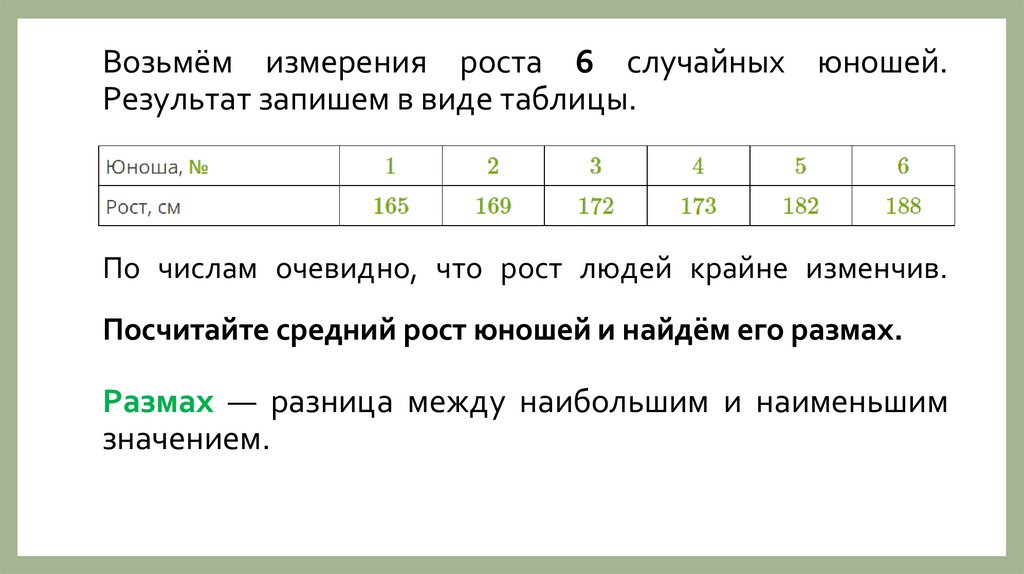
Возьмём измерения роста 6 случайных юношей.
Результат запишем в виде таблицы.
По числам очевидно, что рост людей крайне изменчив.
Посчитайте средний рост юношей и найдём его размах.
Размах — разница между наибольшим и наименьшим
значением.

41.

Среднее арифметическое ряда:
(165+169+172+173+182+188)/6 = 175
Размах:
188−165 = 23.

42.

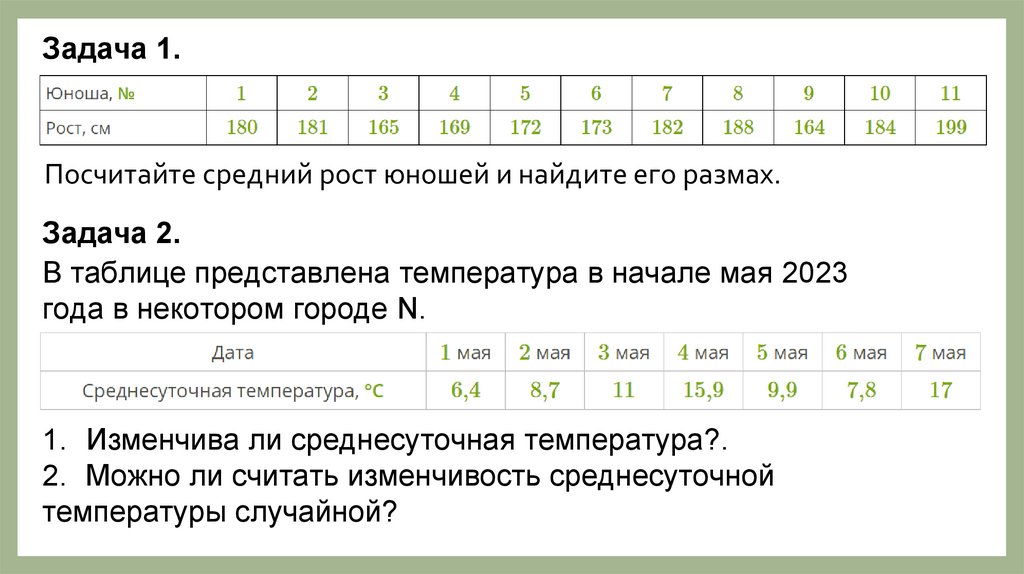
Задача 1.
Посчитайте средний рост юношей и найдите его размах.
Задача 2.
В таблице представлена температура в начале мая 2023
года в некотором городе N.
1. Изменчива ли среднесуточная температура?.
2. Можно ли считать изменчивость среднесуточной
температуры случайной?

43.

Задача 3.
При построении маршрута из пункта A в пункт B навигатор
закладывает примерное время в пути с расчётом на трафик. Серёжа
отправляется в путь в 7 часов утра. Навигатор показывает, что в пути
он проведёт 5,5 ч. Во сколько Серёжа окажется в назначенном месте?
(Ответ укажите в виде десятичной дроби.)

44.

Задача 4.
Численность населения городов измеряется
обычно в тысячах человек. Естественно,
число жителей городов даётся приближенно,
и одна тысяча человек служит единицей
измерения. В таблице представлены данные
по некоторым городам России за 2018 год.
Основываясь на этих данных, найдите
среднюю численность населения, и размах в
данных городах.
(Ответ укажите в целых тысячах человек.)

45.

ТОЧНОСТЬ И
ПОГРЕШНОСТЬ
ИЗМЕРЕНИЙ

46.

Пример 1.
Допустимая погрешность весов зависит от класса точности
весов. Чем выше класс точности, тем меньше погрешность и
тем дороже весы.
Не очень точные весы (lll класс точности), которые рассчитаны
на груз от 20 до 3000 кг, в соответствии с ГОСТ1 имеют разные
допустимые погрешности при разной нагрузке.

47.

Пример 1.
Допустима погрешность весов
при эксплуатации. таб. №1.
Знак ± означает, что отклонение
возможно в любую сторону —
в меньшую или в большую.
Например, если человек массой
ровно 65 кг взвешивается на
напольных весах, то они могут
Показать от 64 до 66 кг.. Наоборот, если напольные весы
показали, что человек имеет массу 65 кг, то истинная масса
человека m находится в пределах от 64 до 66 кг. Это удобно
записать двойным неравенством
64 кг ≤ m ≤ 66 кг

48.

Пример 2.
Согласно ГОСТу автомобильный спидометр при температуре
окружающего воздуха 20 ± 5°С не должен иметь погрешности в
меньшую сторону, а допустимые погрешности в большую
сторону зависят от скорости и указаны в таблице 2. Обратите
внимание:
Погрешность в большую сторону допускается, а в меньшую —
нет. Это сделано для того, чтобы ошибка спидометра не
приводила к превышению скорости.

49.

Пример 2.
Иногда погрешности измеряются
в процентах самой величины.
Это относительные погрешности.
Например,
допустимая
погрешность длины верёвки или
шнура в мотке обычно даётся в
процентах.
Допустима погрешность
автомобильного спидометра. таб. №2.

50.

Пример 2.
На рисунке 1 — катушка, на которую намотан
шнур. На ярлыке указана длина шнура: 250 м +
10%. Это значит, что истинная длина шнура
находится в пределах от 250: 0,9 = 225 (м) до
250 - 1,1 = 275 (м). Это можно выразить двойным
неравенством
225 м ≤ L ≤ 275 м
L – истинная длина шнура.
рис. №1

51.

Задача 1.
Рассмотрите таблицу 1. В ней даны допустимые погрешности
весов в разных диапазонах измерения. Предположим, что весы
исправны и погрешность измерения не выходит за пределы
допустимой. Запишите с помощью двойного неравенства
границы, в которых находится истинное значение массы m
некоторого груза, если при взвешивании этого груза весы
показывают:
a) 38 кг;
б) 129 кг;
в) 2956 кг;
г) 2543 кг.

52.

Задача 2.
Рассмотрите таблицу 2. Предположим, что автомобильный
спидометр исправен. Укажите с помощью двойного неравенства
границы истинной скорости и автомобиля, если спидометр
показывает:
а) 28 км/ч;
б) 68 км/ч;
в) 96 км/ч;
г) 127 км/ч.
Задача 3.
На мотке верёвки указано, что длина верёвки составляет
30 м ± 5%. В каких пределах может быть заключена истинная
длина верёвки?

53.

ТЕНДЕНЦИИ И
СЛУЧАЙНЫЕ
ОТКЛОНЕНИЯ

54.

Тенденция (тренд) — характерное, устойчивое изменение. Как
правило, тенденция обусловлена долгосрочными факторами,
которые заставляют величину расти или убывать.
В отличии от тенденции, случайные колебания непредсказуемы,
поскольку
вызваны
кратковременными
случайными
и
разнонаправленными факторами.

55.

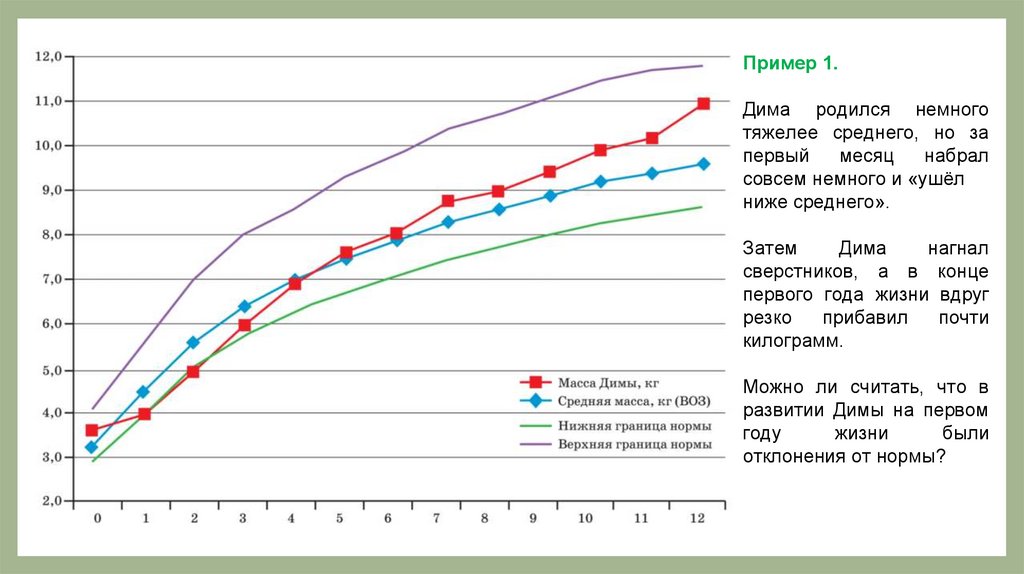
Пример 1.
Дима родился немного
тяжелее среднего, но за
первый
месяц
набрал
совсем немного и «ушёл
ниже среднего».
Затем
Дима
нагнал
сверстников, а в конце
первого года жизни вдруг
резко
прибавил
почти
килограмм.
Можно ли считать, что в
развитии Димы на первом
году
жизни
были
отклонения от нормы?

56.

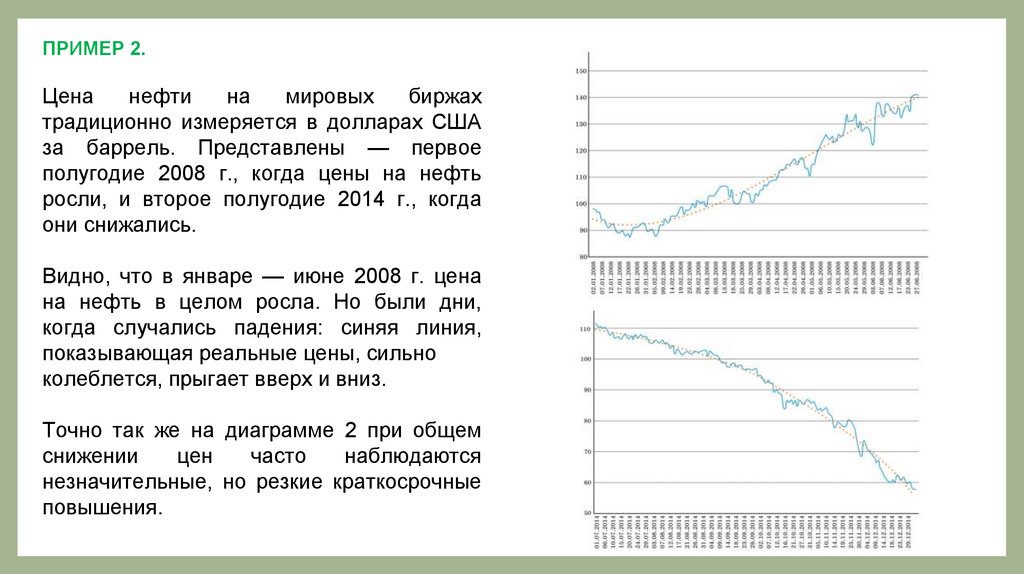
ПРИМЕР 2.
Цена
нефти
на
мировых
биржах
традиционно измеряется в долларах США
за баррель. Представлены — первое
полугодие 2008 г., когда цены на нефть
росли, и второе полугодие 2014 г., когда
они снижались.
Видно, что в январе — июне 2008 г. цена
на нефть в целом росла. Но были дни,
когда случались падения: синяя линия,
показывающая реальные цены, сильно
колеблется, прыгает вверх и вниз.
Точно так же на диаграмме 2 при общем
снижении
цен
часто
наблюдаются
незначительные, но резкие краткосрочные
повышения.

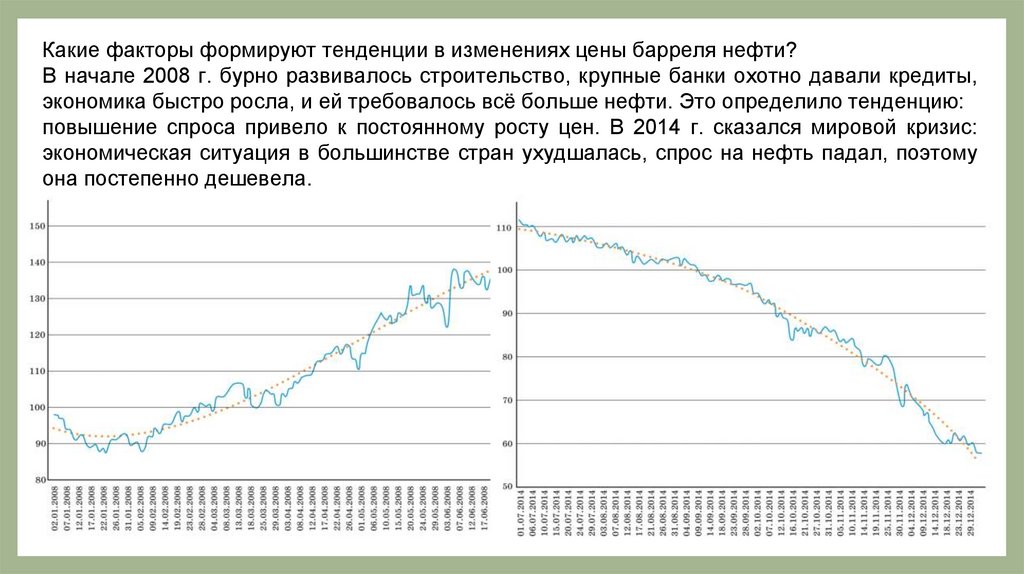
57.

Какие факторы формируют тенденции в изменениях цены барреля нефти?
В начале 2008 г. бурно развивалось строительство, крупные банки охотно давали кредиты,
экономика быстро росла, и ей требовалось всё больше нефти. Это определило тенденцию:
повышение спроса привело к постоянному росту цен. В 2014 г. сказался мировой кризис:
экономическая ситуация в большинстве стран ухудшалась, спрос на нефть падал, поэтому
она постепенно дешевела.

58.

Часто изменчивость в природных, экономических и социальных явлениях
состоит из двух составляющих. Первая составляющая — тенденция,
которая обусловлена серьёзными и долгосрочными факторами. Вторая
составляющая — случайные отклонения, вызванные разнонаправленными
краткосрочными действиями, которые зачастую невозможно предвидеть.
Одна из важных задач статистики — научиться выделять тенденции в
изменчивых явлениях и отличать их от незначительных случайных
колебаний.

59.

Задачи.
1. Приведите свой пример величины, имеющей постоянное среднее
значение, вокруг которого наблюдаются случайные колебания.
2. Приведите свой пример величины, имеющей возрастающую тенденцию.

60.

СТАТИСТИЧЕСКАЯ
УСТОЙЧИВОСТЬ И
ОЦЕНКИ С ПОМОЩЬЮ
ВЫБОРКИ

61.

Частоты, средние значения и другие характеристики многих изменчивых
величин мало отличаются от таких же характеристик в другой случайной
выборке или во всей совокупности данных. Это свойство изменчивых
величин называют статистической устойчивостью.
Чтобы статистическая устойчивость проявила себя в двух выборках, нужно
чтобы эти выборки были сделаны в одинаковых условиях. Если в одной и
той же квартире измерять напряжение электрической сети первый раз
днём, второй раз вечером, когда почти у всех соседей горит свет, а третий
раз ночью, то, скорее всего, все три выборки будут значительно
отличаться друг от друга.

62.

Чтобы выборка хорошо отражала свойства всей совокупности данных (их
может быть бесконечно много), лучше всего, чтобы эта выборка была
сделана случайным образом. Например, измерения напряжения нужно
проводить на протяжении дли- тельного времени в случайные моменты.
Чем больше объём выборки (количество значений), тем лучше, как
правило, проявляет себя статистическая устойчивость.
Статистическая устойчивость даёт возможность оценивать (приближённо
находить) частоты и средние значения в бесконечных или плохо доступных
массивах данных. При этом нужно помнить, что в силу случайной
изменчивости оценки, сделанные с помощью выборки, приблизительные

63.

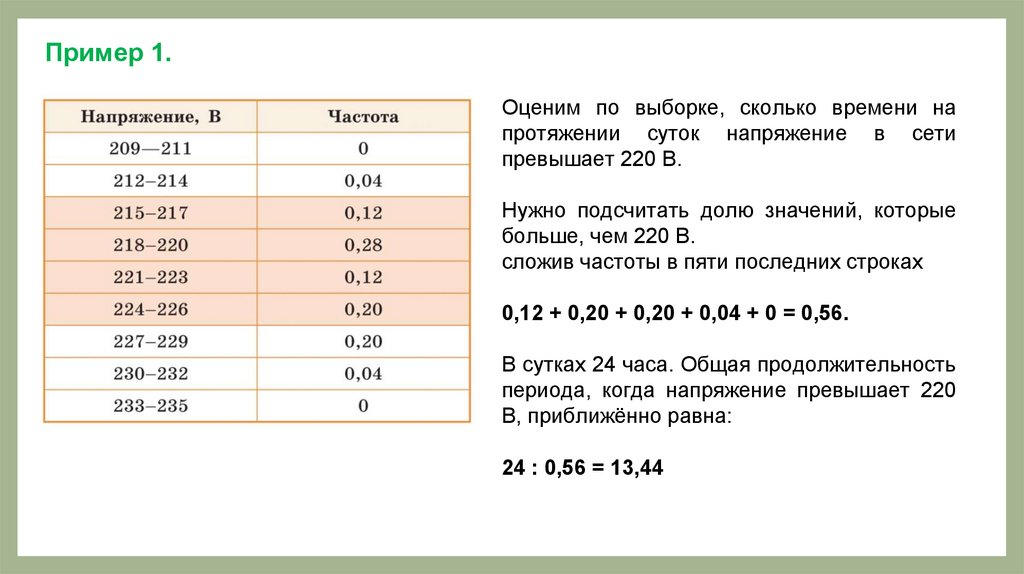
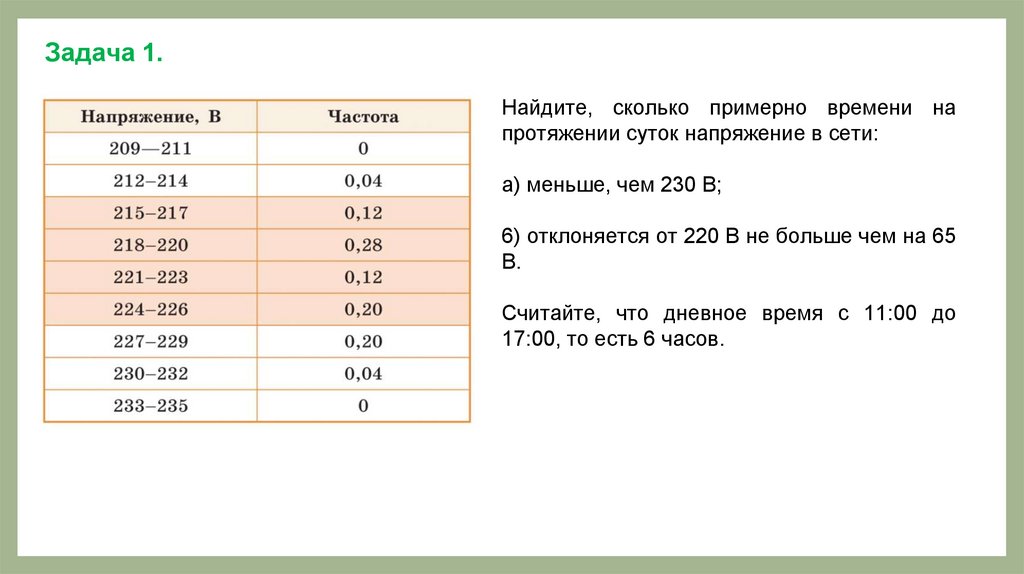
Пример 1.
Оценим по выборке, сколько времени на
протяжении суток напряжение в сети
превышает 220 В.
Нужно подсчитать долю значений, которые
больше, чем 220 В.
сложив частоты в пяти последних строках
0,12 + 0,20 + 0,20 + 0,04 + 0 = 0,56.
В сутках 24 часа. Общая продолжительность
периода, когда напряжение превышает 220
В, приближённо равна:
24 : 0,56 = 13,44

64.

Задача 1.
Найдите, сколько примерно времени на
протяжении суток напряжение в сети:
а) меньше, чем 230 В;
6) отклоняется от 220 В не больше чем на 65
В.
Считайте, что дневное время с 11:00 до
17:00, то есть 6 часов.

65.

ГРАФЫ.
ВЕРШИНЫ И РЁБРА

66.

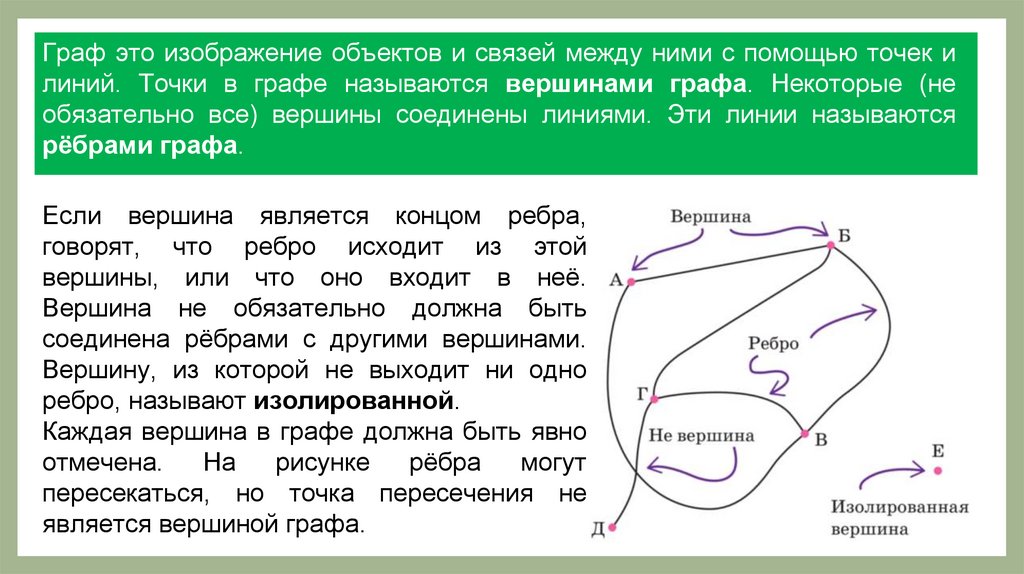
Граф это изображение объектов и связей между ними с помощью точек и
линий. Точки в графе называются вершинами графа. Некоторые (не
обязательно все) вершины соединены линиями. Эти линии называются
рёбрами графа.
Если вершина является концом ребра,
говорят, что ребро исходит из этой
вершины, или что оно входит в неё.
Вершина не обязательно должна быть
соединена рёбрами с другими вершинами.
Вершину, из которой не выходит ни одно
ребро, называют изолированной.
Каждая вершина в графе должна быть явно
отмечена.
На
рисунке
рёбра
могут
пересекаться, но точка пересечения не
является вершиной графа.

67.

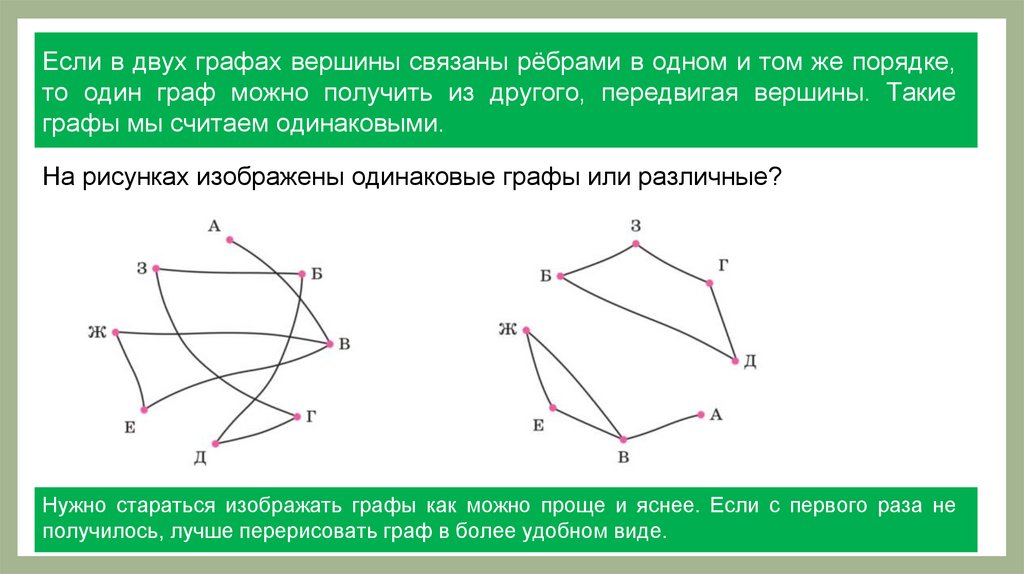
Если в двух графах вершины связаны рёбрами в одном и том же порядке,
то один граф можно получить из другого, передвигая вершины. Такие
графы мы считаем одинаковыми.
На рисунках изображены одинаковые графы или различные?
Нужно стараться изображать графы как можно проще и яснее. Если с первого раза не
получилось, лучше перерисовать граф в более удобном виде.

68.

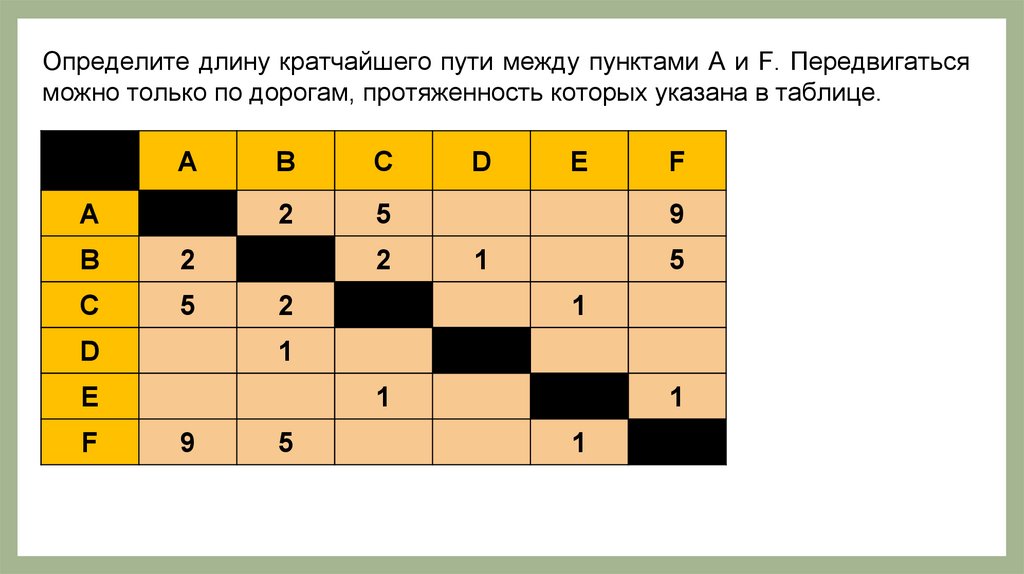
Определите
Если
в двух графах
длину кратчайшего
вершины связаны
пути между
рёбрами
пунктами
в одном
А и F.
том
Передвигаться
же порядке,
то один
можно
только
графпоможно
дорогам,
получить
протяженность
из другого,
которых
передвигая
указана вершины.
в таблице. Такие
графы мы считаем одинаковыми.
A
A
B
2
C
5
D
B
C
2
5
2
2
E
F
9
1
5
1
1
E
F
D
1
9
5
1
1

69.

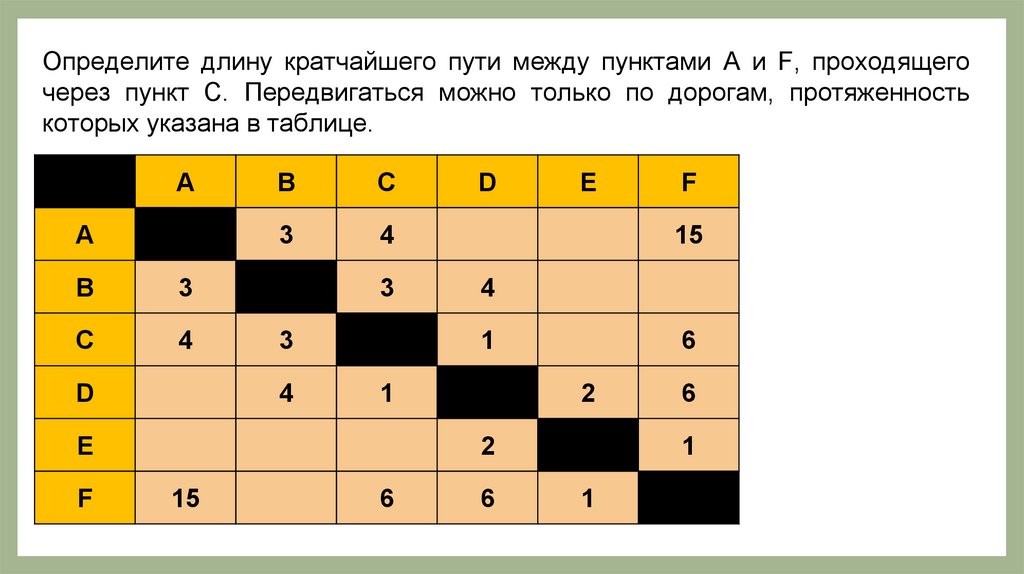
Определите
Если
в двух графах
длину кратчайшего
вершины связаны
пути между
рёбрами
пунктами
в одномAи итом
F, же
проходящего
порядке,
то один
через
пункт
графС. можно
Передвигаться
получить можно
из другого,
толькопередвигая
по дорогам,
вершины.
протяженность
Такие
графы мы
которых
указана
считаем
в таблице.
одинаковыми.
A
A
B
3
C
4
D
B
C
3
4
3
3
4
E
4
1
6
2
2
15
6
F
15
1
E
F
D
6
6
1
1

70.

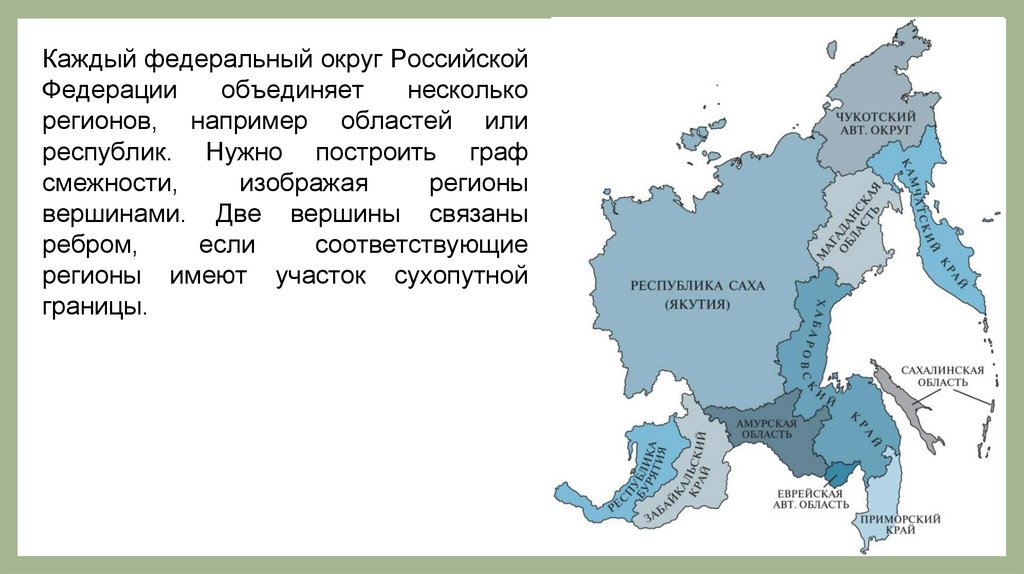
Каждый
федеральный
округ Российской
Если в двух
графах вершины
связаны рёбрами в одном и том же порядке,
Федерации
несколько
то один граф объединяет
можно получить
из другого, передвигая вершины. Такие
регионов,
например
областей или
графы мы считаем
одинаковыми.
республик. Нужно построить граф
смежности,
изображая
регионы
вершинами. Две вершины связаны
ребром,
если
соответствующие
регионы имеют участок сухопутной
границы.