Принятие решений в сложных системах

1.

Принятие решений в
сложных системах

2. Основные понятия, используемые в теории принятия решений

Теория принятия решений – это наука, изучающая
закономерности процесса принятия решений, опирающаяся на
методы и технологию системного подхода в поиске
эффективных решений.
Под принятием решений понимается процесс человеческой
деятельности, направленный на выбор наилучшего варианта
действий. Модели, описывающие поведение людей, широко
используются в исследовании операций.
Под исследованием операций понимают применение
математических, количественных методов для обоснования
решений во всех областях целенаправленной человеческой
деятельности.
2

3. Основные понятия, используемые в теории принятия решений

Под операцией
будем понимать систему действий,
объединенных единым замыслом и направленных к
достижению определенной цели. Операция всегда является
управляемым мероприятием.
От нас зависит выбор каких-то параметров, характеризующих
способ ее организации. Всякий определенный выбор зависящих
от нас параметров будем называть решением.
Само принятие решения выходит за рамки исследования
операций и относится к компетенции ответственного лица (или
группы лиц), которым предоставлено право окончательного
выбора.
3

4. Основные понятия, используемые в теории принятия решений

К основным понятиям теории принятия решений относятся:
• проблемная ситуация;
• решение;
• функция принятия решений;
• задачи принятия решений;
• лицо, принимающее решение (ЛПР);
• процесс принятия решений.
Проблема имеет место, если фактическое состояние системы
не соответствует желаемому. Выработка плана действий по
устранению проблемы составляет сущность задачи принятия
решений.
4

5. Основные понятия, используемые в теории принятия решений

Проблемы могут возникать в следующих случаях:
− функционирование системы в данный момент не
обеспечивает достижения поставленных целей;
− функционирование системы в будущем не обеспечит
достижения поставленных целей;
− необходимо изменение целей деятельности.
Проблема всегда связана с определенными условиями,
которые обобщенно называют ситуацией. Совокупность
проблемы и ситуации образует проблемную ситуацию.
Выявление и описание проблемной ситуации дает исходную
информацию для постановки задачи принятия решений.
5

6. Основные понятия, используемые в теории принятия решений

В соответствии с системным подходом исходная информация
о проблемной ситуации, по которой необходимо принимать
решение, должна включать:
− определение степени соответствия фактических (или
прогнозируемых) целей и подцелей требуемым;
− определение факторов (причин) возникновения
проблемной ситуации и необходимых ресурсов для решения
проблемной
ситуации
(социальных,
экономических,
технических, интеллектуальных, энергетических и др.)
На всех стадиях жизненного цикла систем (от создания –
зарождения и до гибели – утилизации) необходимо принимать
большое количество решений. Эти решения, в зависимости от
типа систем, могут иметь социально-экономический,
организационный, технический, информационный и другой
6
характер.

7. Основные понятия, используемые в теории принятия решений

Субъектом всякого решения является лицо, принимающее
решение (ЛПР). В процессе принятия решений люди могут играть
разные роли. Человек, фактически осуществляющий выбор
наилучшего
варианта
действий,
называют
лицом,
принимающим решения (ЛПР).
Понятие ЛПР является собирательным. Это может быть одно
лицо – индивидуальное ЛПР или группа лиц, вырабатывающих
коллективное решение, групповое ЛПР.
Лицо, принимающее решение (ЛПР) – субъект, задающий
приоритеты, в интересах которого принимается решение. Как
правило, ЛПР стремится получить наилучшее (оптимальное,
удовлетворительное), с его точки зрения, решение.
7

8. Основные понятия, используемые в теории принятия решений

Под наилучшим решением мы будем понимать решение,
множество отрицательных последствий которого минимально
по сравнению с другими альтернативами.
Выбор решения зависит:
• от информации, имеющейся у ЛПР о данной предметной
области, т.е. о множестве альтернатив и состоянии
окружающей среды, а также
• от того, как он устанавливает приоритеты, т.е. от его стиля
мышления, стратегии поведения.
8

9. Основные понятия, используемые в теории принятия решений

Например, один любит рисковать, другой чрезмерно
осторожничает, третий предпочитает “золотую середину” и т.п.
Таким образом, ЛПР обладает некоторой свободой выбора.
Однако если он не учитывает особенности решаемой
проблемы, ее влияние на внешние системы, то полученное
решение может сильно расходиться с реальностью и привести
к значительным отрицательным последствиям. Задачи
принятия решений могут различаться типом исхода,
структурой предпочтений, количеством оценочных критериев,
моделью оптимизации и т.п.

10. Основные понятия, используемые в теории принятия решений

Другой ролью, которую может играть человек в процессе
принятия решений, является роль руководителя или
участника активной группы – группы людей, имеющих общие
интересы и старающихся оказать влияние на процесс выбора и
его результат.
Для помощи ЛПР в сборе и анализе информации и
формировании решений привлекаются эксперты, т.е.
профессионала в той или иной области, к которому обращаются
за оценками или рекомендациями.
Понятие эксперта в теории принятия решений трактуется в
широком смысле и включает в себя сотрудников аппарата
управления, подготавливающих решение, ученых и практиковспециалистов.
10

11. Основные понятия, используемые в теории принятия решений

При подготовке сложных решений иногда принимает
участие консультант по принятию решений. Его роль состоит
в организации процесса принятия решений: помощи ЛПР в
правильной постановке задачи, выявлении позиций активных
групп, организации работы с экспертами.
Особое место занимает лицо (группа лиц), владеющее
математическими методами и использующее их для анализа
операции.
Это
лицо
(исследователь
операции, исследователь-аналитик) само решений не
принимает, а лишь помогает в этом.
11

12. Основные понятия, используемые в теории принятия решений

Решение является одним из видов мыслительной
деятельности и проявлением воли человека и имеет свои
характерные признаки.
К ним относятся:
− наличие выбора из множества возможных решений;
− выбор ориентирован на сознательное достижение целей;
− выбор основан на сформировавшейся установке к
действию.
Первый признак определяет необходимость существования
альтернативных решений. Если нет альтернатив, то нет выбора и,
следовательно, нет решения, поскольку отпадает необходимость
в мыслительно-волевом акте.
Для постановки задачи принятия решений необходимо
иметь хотя бы две альтернативы.
12

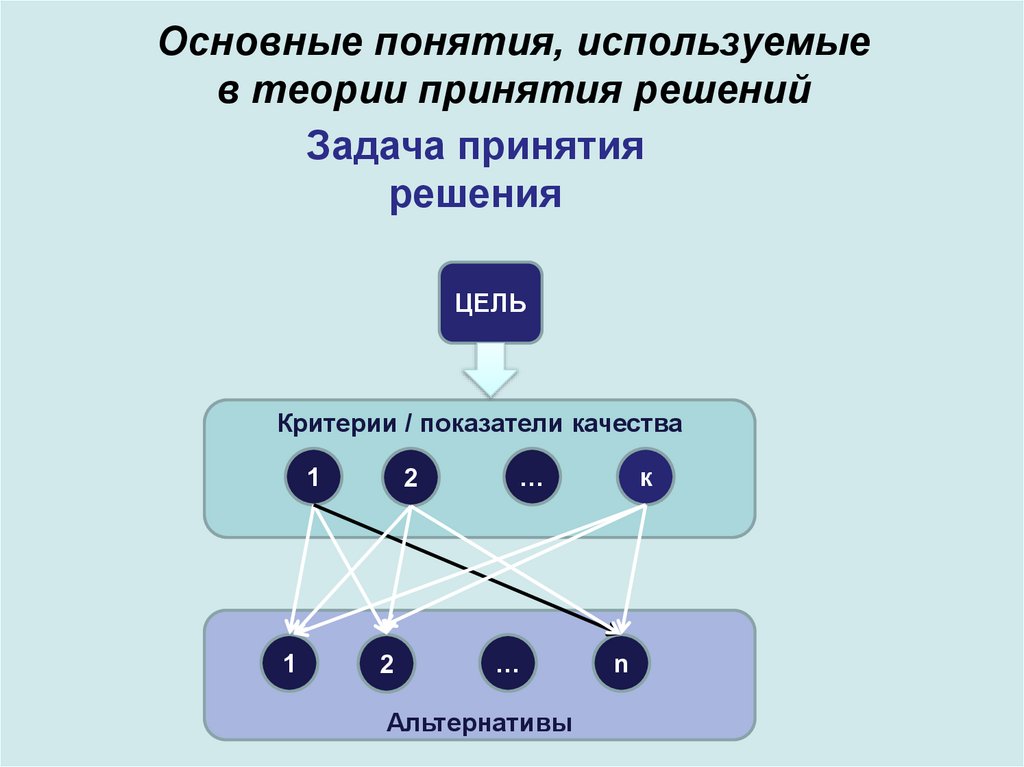
13. Основные понятия, используемые в теории принятия решений

Задача принятия
решения
ЦЕЛЬ
Критерии / показатели качества
1
1
2
2
…
…
Альтернативы
к
n

14.

Критерии оценки альтернатив
Альтернативы
Независимые
Зависимые
Независимыми являются те альтернативы, любые действия с
которыми (удаление из рассмотрения, выделение в качестве
лучшей) не влияют на качество других альтернатив.
При зависимых альтернативах оценки одних из них
оказывают влияние на качество других. Имеются различные
типы зависимости альтернатив. Наиболее простым является
групповая зависимость: если решено рассматривать хотя бы
одну альтернативу из группы, то надо рассматривать и всю
группу.
14

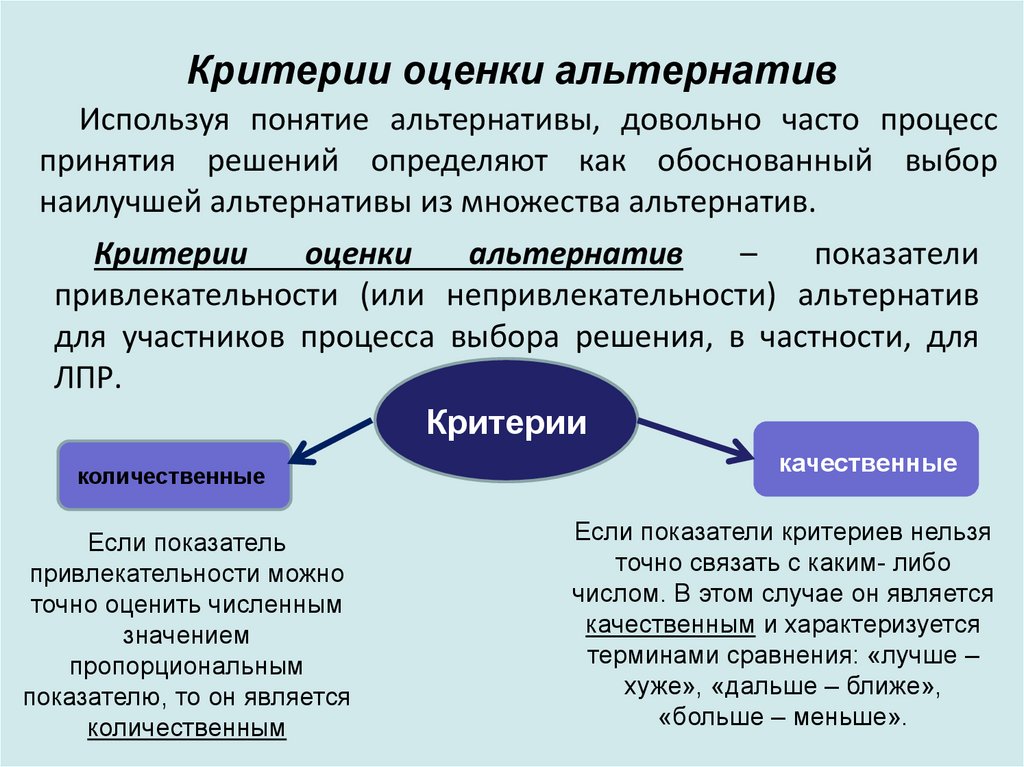
15. Критерии оценки альтернатив

Используя понятие альтернативы, довольно часто процесс
принятия решений определяют как обоснованный выбор
наилучшей альтернативы из множества альтернатив.
Критерии
оценки
альтернатив
–
показатели
привлекательности (или непривлекательности) альтернатив
для участников процесса выбора решения, в частности, для
ЛПР.
Критерии
количественные
Если показатель
привлекательности можно
точно оценить численным
значением
пропорциональным
показателю, то он является
количественным
качественные
Если показатели критериев нельзя
точно связать с каким- либо
числом. В этом случае он является
качественным и характеризуется
терминами сравнения: «лучше –
хуже», «дальше – ближе»,
«больше – меньше».

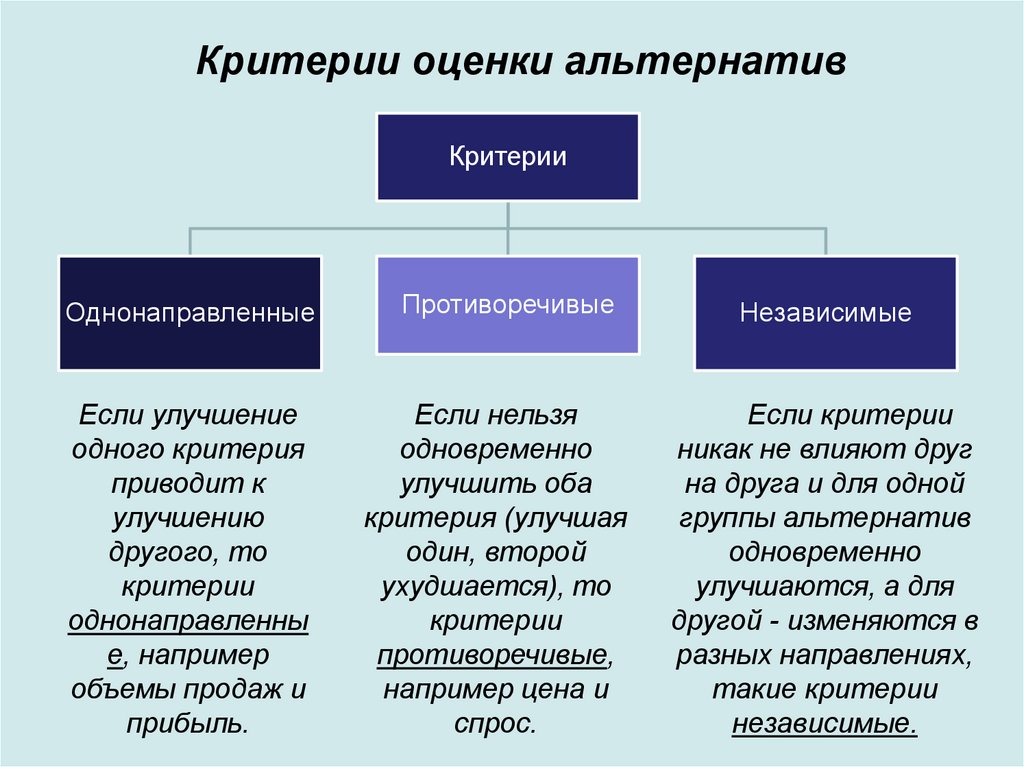
16. Критерии оценки альтернатив

Критерии
Однонаправленные
Противоречивые
Независимые
Если улучшение
одного критерия
приводит к
улучшению
другого, то
критерии
однонаправленны
е, например
объемы продаж и
прибыль.
Если нельзя
одновременно
улучшить оба
критерия (улучшая
один, второй
ухудшается), то
критерии
противоречивые,
например цена и
спрос.
Если критерии
никак не влияют друг
на друга и для одной
группы альтернатив
одновременно
улучшаются, а для
другой - изменяются в
разных направлениях,
такие критерии
независимые.

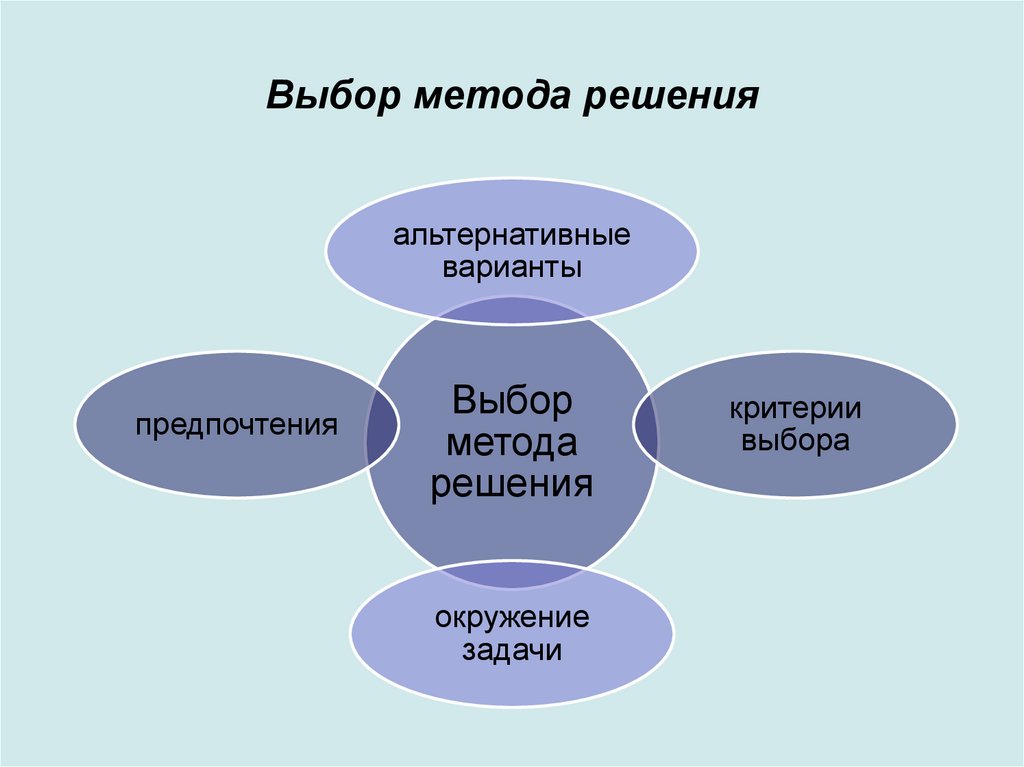
17. Выбор метода решения

альтернативные
варианты
предпочтения
Выбор
метода
решения
окружение
задачи
критерии
выбора

18. Основные понятия, используемые в теории принятия решений

Важной
особенностью
решения
является
целенаправленность и сознательность выбора.
Бесцельный
выбор,
импульсивное
действие
не
рассматриваются как решение.
Последний
признак
подчеркивает
необходимость
осуществления волевого акта при выборе решения.
Решение должно приводить к действию, поэтому человек,
принимающий решение, формирует его через борьбу мотивов
и выработку установки – состояния готовности к действию.
18

19. Типология решений

Основные понятия, используемые
в теории принятия решений
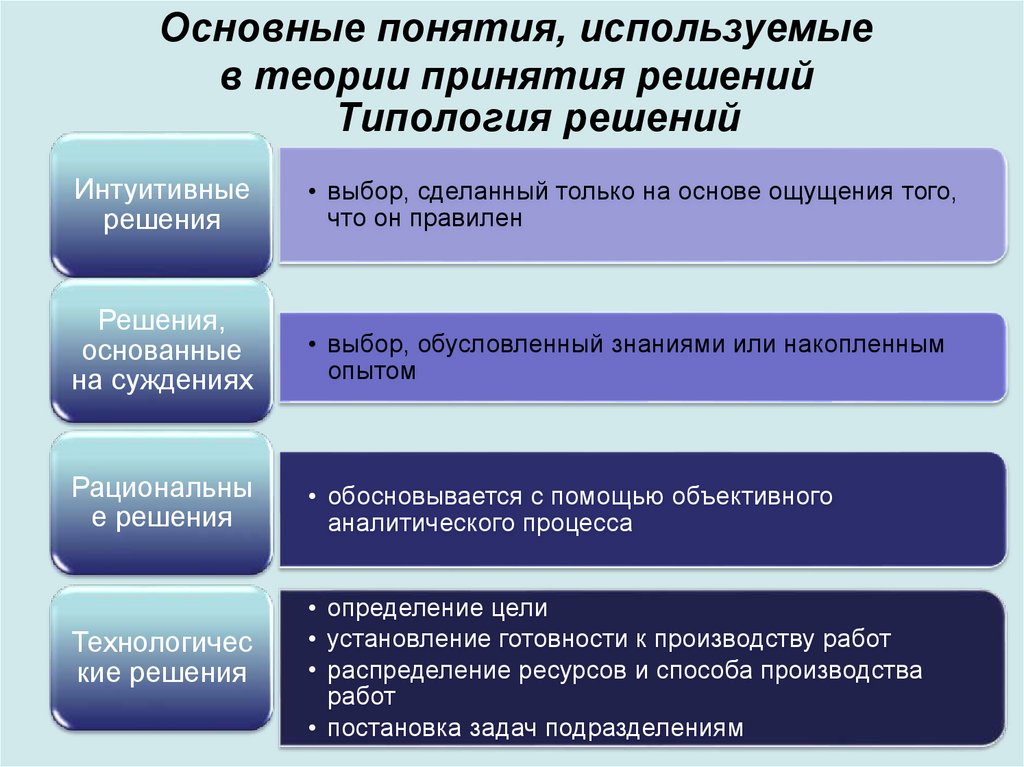
Типология решений
Интуитивные
решения
• выбор, сделанный только на основе ощущения того,
что он правилен
Решения,
основанные
на суждениях
• выбор, обусловленный знаниями или накопленным
опытом
Рациональны
е решения
• обосновывается с помощью объективного
аналитического процесса
Технологичес
кие решения
• определение цели
• установление готовности к производству работ
• распределение ресурсов и способа производства
работ
• постановка задач подразделениям

20. Основные понятия, используемые в теории принятия решений

Решение называется допустимым, если оно удовлетворяет
ограничениям:
• правовым,
• морально-этическим,
• ресурсным.
Решение называется оптимальным (наилучшим), если оно
обеспечивает экстремум (максимум или минимум) критерия
выбора при индивидуальном ЛПР или удовлетворяет принципу
согласования при групповом ЛПР.
Обобщенной характеристикой решения является его
эффективность. Эта характеристика включает эффект решения,
отнесенный к затратам на достижение целей, определяет
степень достижения целей. Решение тем эффективнее, чем
больше степень достижения целей и меньше затраты на их
20
реализацию.

21. Основные понятия, используемые в теории принятия решений

Функция принятия решений есть постоянно решаемая в
процессе управления задача. Трактовка функции принятия
решения как задачи позволяет более четко сформулировать ее
содержание, определить технологию и методы решения. Задача
принятия решений направлена на определение наилучшего
(оптимального) способа действий для достижения поставленных
целей.
Для
осуществления
выбора
наилучшего
решения
индивидуальное ЛПР определяет критерий выбора. Групповые
ЛПР производят выбор на основе принципа согласования.
Принятие решений происходит во времени, поэтому вводится
понятие процесса принятия решений. Процесс принятия
решений имеет место практически в любой сфере
целенаправленной человеческой деятельности.
21

22. Основные понятия, используемые в теории принятия решений

Этот процесс состоит из последовательности этапов и
операций и направлен на устранение проблемной ситуации.
В процессе принятия решений формируются альтернативные
(взаимоисключающие) варианты решений и оценивается их
предпочтительность.
Предпочтение – это интегральная оценка качества решений,
основанная на объективном анализе (знании, опыте,
проведении расчетов и экспериментов) и субъективном
понимании ценности, эффективности решений.
22

23. Выбор как реализация цели

• Под принятием решения понимается выбор одного или
нескольких вариантов решения проблемы из некоторого
исходного множества допустимых вариантов. Это множество
будем называть множеством альтернатив X, а любое решение x
из него – альтернативой, x X. Поэтому часто задачу принятия
решений называют задачей выбора.
• Исходное множество альтернатив может быть правильно
сформировано только на основе условий и ограничений со
стороны внешних систем, которые затрагивает решаемая
проблема. Если лицо, принимающее решение (ЛПР) не
учитывает требования внешних систем, то множество
альтернатив оказывается неполным, а выбор ограниченным, и
хорошего решения получить не удается.
• Последствием принятия решения назовем событие (исход),
необходимость или возможность появления которого
определяется данным решением.

24. Подходы к структуризации процесса принятия решений

25.

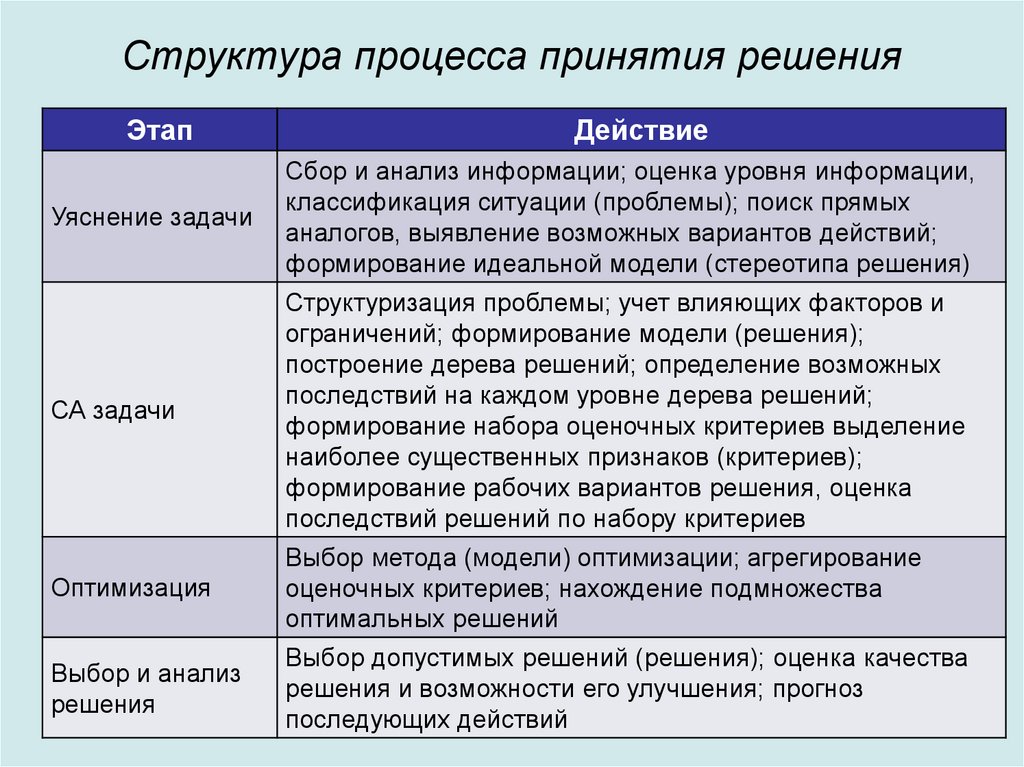
26. Структура процесса принятия решения

Этап
Действие
Уяснение задачи
Сбор и анализ информации; оценка уровня информации,
классификация ситуации (проблемы); поиск прямых
аналогов, выявление возможных вариантов действий;
формирование идеальной модели (стереотипа решения)
СА задачи
Структуризация проблемы; учет влияющих факторов и
ограничений; формирование модели (решения);
построение дерева решений; определение возможных
последствий на каждом уровне дерева решений;
формирование набора оценочных критериев выделение
наиболее существенных признаков (критериев);
формирование рабочих вариантов решения, оценка
последствий решений по набору критериев
Оптимизация
Выбор метода (модели) оптимизации; агрегирование
оценочных критериев; нахождение подмножества
оптимальных решений
Выбор и анализ
решения
Выбор допустимых решений (решения); оценка качества
решения и возможности его улучшения; прогноз
последующих действий

27.

Стратегия поиска решения зависит от имеющейся информации о
задаче и включает способ выбора альтернатив, определяемый
структурой предпочтений лица принимающего решение (ЛПР) и
метод
(модель)
оптимизации,
обусловливающий
способ
агрегирования критериев.
Способ выбора альтернатив может предусматривать поиск
наилучшего решения, удовлетворительного решения, наиболее
предпочтительной альтернативы, недоминируемой альтернативы,
возможной альтернативы, и т.п.
27

28.

• Классификация задач принятия решений. Задачи
принятия управленческих решений группируются в
зависимости от набора некоторых классификационных
признаков. Задача классификации, в свою очередь, позволяет
выделить для группы однородных задач наиболее
эффективные методы их решения, в частности оптимальные
методы принятия решений в различных управленческих и
производственных задачах.
• Сама процедура классификации сводится к ограничению
выбора для конкретной задачи. Для этого и используется ряд
классификационных признаков. Существует несколько
различных подходов к классификации задач принятия
решений
(ЗПР),
использующих
различный
набор
классификационных признаков.
28

29.

• Однако большинство из них опираются на следующие
факторы группировки: характер субъекта (ЛПР), содержание
ЗПР, количество целей, влияние времени, значимость решений
и др.
• Свою очередь, каждый из классификационных признаков
включает несколько вложенных параметров кластеризации
ЗПР.
29

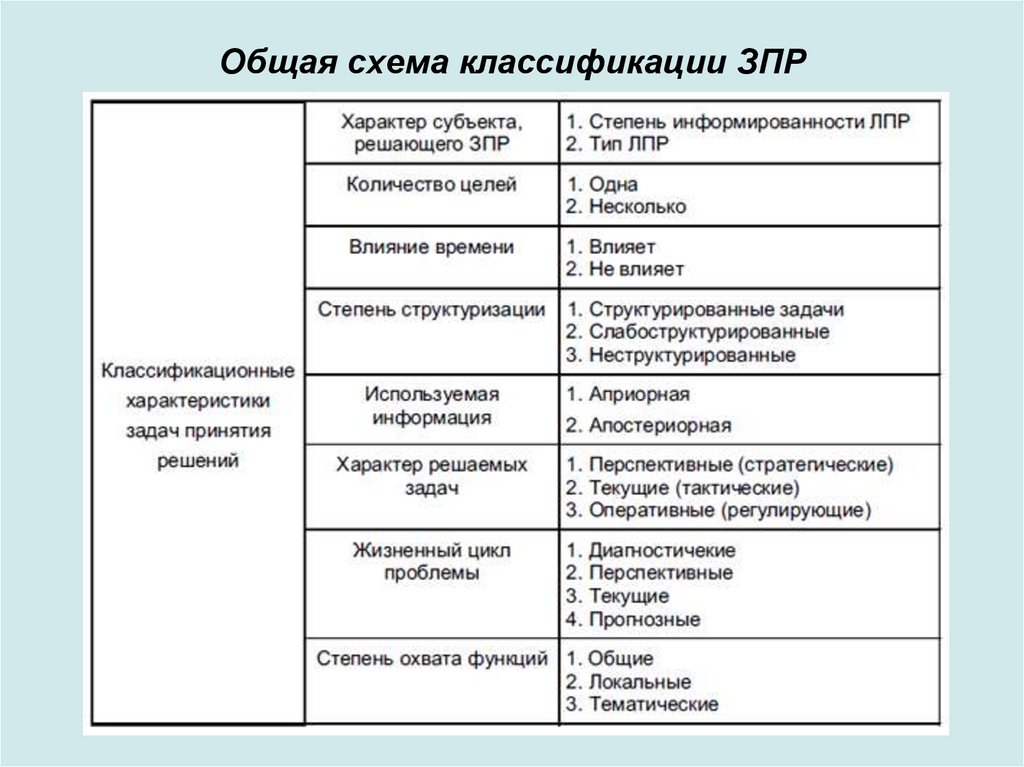
30. Общая схема классификации ЗПР

31.

• Признак
характер
субъекта
задачи
принятия
решений описывает степень его информированности о проблемной
ситуации (ПС) в экономической системе и конкретном типе ЛПР.
• По информированности руководителя (ЛПР) о состоянии
системы, задачи ПР разбиваются на:
• задачи, решаемые в условиях полной определенности, когда
известны все составляющие и характеристики системы. Здесь
понятие
определенности
характеризуется
полнотой
и
достоверностью информации для принятия решений. К таким,
определенным задачам относятся: задачи размещения ресурсов,
назначения работ, управления запасами, транспортные и др.;
задачи,
решаемые
в
условиях
вероятностной
определенности (риска). Обычно это стохастические задачи, когда
известны лишь статистические данные о факторах, влияющих на
выработку решений. Решение таких задач формируется на базе
теории
статистических
решений.
Обобщенным
критерием
оптимального решения здесь является средний риск.
• задачи, решаемые в условиях неопределенности, когда
отсутствует полная информация о факторах и характеристика
проектируемой системы или информация характеризует ситуацию с
некоторой степенью нечеткости, размытости.

32.

Характерны
большая
неполнота
информации,
малая
достоверность, сложные взаимосвязи между факторами.
задачи,
решаемые
в
условиях
стратегической
неопределенности, с активным противодействием внешней или
внутренней структуры системы. То есть в таких задачах необходимо
учитывать влияние на исход решения лиц, преследующих
противоположные общесистемным или неизвестные цели.
По типу ЛПР, участвующих в решении задачи, различают:
• задачи индивидуального выбора, когда решения формирует и
принимает отдельный субъект — лицо, принимающее решение
(руководитель, главный специалист или др.), наделенное
полномочиями
и
ресурсами
для
принятия
решений
в
соответствующей сфере и на соответствующем этапе процесса
управления;
• задачи группового выбора, когда в качестве ЛПР участвует
группа менеджеров или консультантов-специалистов по конкретным
проблемам.

33.

По степени используемой информации задачи могут быть
сгруппированы в виде:
• задач, решаемых на основе априорных данных. Задачи первого
типа характерны для вполне определенных проблемных ситуаций,
так как для их решения используется достоверная (априорная),
точная, заранее известная информация.
• задач, решаемых на основе апостериорных данных. В условиях
неопределенности априорной информации недостаточно, поэтому
для ее пополнения необходимо доопределить исходную ситуацию
проведением эксперимента, который и дает дополнительную
информацию.
По количеству целей, стоящих перед ЛПР при решении задачи
ПР, они разбиваются на:
• однокритериальные задачи (скалярные задачи), в которых
сформулирована только одна цель (критерий), относительно
которой решается задача;
• многокритериальные задачи (векторные), в которых в
качестве цели решения выступает несколько критериев, достижение
которых для эффективного решения задачи должно быть
одновременным.

34.

По
степени
воздействия
на
решение
задачи
фактора времени они разбиваются на:
• статические задачи, в которых время принятия решения не
играет большой роли;
• динамические задачи, эффективность решения которых зависит
от времени, выделяемого (имеющегося) на решение. В свою очередь,
динамические задачи можно разделить по длительности воздействия
времени на:
- долгосрочные, рассчитанные на весь период существования
проблемы;
- среднесрочные, которые должны осуществиться в недалеком
будущем;
- краткосрочные, которые выполняются в течение короткого
периода времени.
По степени структуризации элементов проблемной ситуации
выделяют:
• хорошо структурированные задачи, в которых зависимости
между факторами ПС определены количественно;

35.

• неструктурированные задачи, в которых невозможно задать
количественные зависимости между факторами (признаками) в
описании задачи;
• слабоструктурированные, т. е. смешанные задачи с
количественно и качественно определенными признаками.
Под структурированными задачами здесь понимаются задачи
принятия решений, обладающие следующими свойствами:
• переменные определены в виде скалярного или векторного
числового значения;
• цели определяются единственной, четко выраженной целевой
функцией;
• можно построить четкий алгоритм решения.
На практике руководителю высшего уровня управления почти
всегда приходится иметь дело со слабоструктурированными или
неструктурированными задачами принятия решений.

36.

По характеру различаются следующие виды управленческих
решений:
• перспективные (стратегические), определяющие главные
направления развития организации;
• текущие (тактические), которые предусматривают достижение
более частных целей;
оперативные
(регулировочные),
направленные
на
восстановление изменение) пропорций, устранение отклонений в
функционировании организации и отдельных ее частей и т. п.
По жизненному циклу существования проблемы можно
выделить решения:
диагностические,
рассчитанные
на
решение
задач
исследования и оценки показателей, диагностирующих уровень
кризисного состояния предприятия;
• перспективные, решающие задачи устранения причин
возникновения проблем;
• текущие, решающие задачи текущего управления;
• прогнозные, решающие задачи прогнозирования развития
проблемной ситуации.

37.

По степени охвата функций управления различаются решения:
• общие, охватывающие всю управляемую систему;
• локальные — отдельных подразделений организации (цехов,
участков, производств, отделов, служб);
• тематические, относящиеся к конкретным функциям
управления.
Управленческие решения иногда классифицируют по
принадлежности их к директивным, нормативным или косвенным
решениям.
• Директивные решения принимаются на высшем уровне
управления фирмой и являются обязательными для исполнения.
• Нормативные, принимаемые на всех уровнях управления
организацией, оформляются в виде приказов, распоряжений. Они не
содержат альтернативы.
• Косвенные решения носят стимулирующий характер и
способствуют изменениям в работе фирмы при помощи
совершенствования инструментального обеспечения управления —
экономических, финансовых, правовых, социальных и других рычагов.

38. Классификация задач принятия решения

Классификационный
Разновидность задачи принятия решений
признак
Новизна задачи
Задача имеется в базе знаний (есть алгоритм
(алгоритм решения
решения): задачи нет в базе знаний, но есть
наличие аналога)
аналоги: задача не имеет аналогов
Tип исхода
Детерминированный исход (в условиях
(информационная среда определенности); случайный исход (в условиях
задачи, уровень
риска, в условиях неопределенности); нечеткий
информации)
исход (в условиях нечеткости)
Необходимость решения новой задачи; изменение
Вид проблемной
условий функционирования системы; появление
ситуации
новой информации; сбой в работе (отказ) системы
или ее элементов
Метод описания и
Декларативный; процедурный; комбинированный
представления
(сочетание нескольких методов)
информации
38

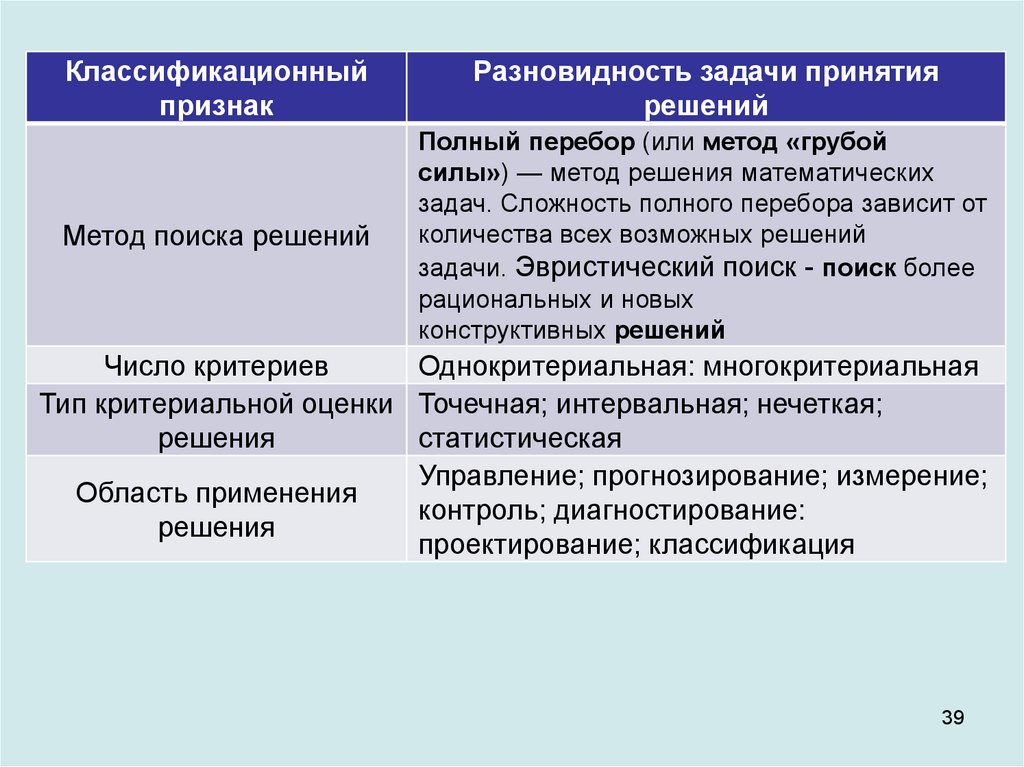
39.

Классификационный
признак
Разновидность задачи принятия
решений
Метод поиска решений
Полный перебор (или метод «грубой
силы») — метод решения математических
задач. Сложность полного перебора зависит от
количества всех возможных решений
задачи. Эвристический поиск - поиск более
рациональных и новых
конструктивных решений
Число критериев
Однокритериальная: многокритериальная
Тип критериальной оценки Точечная; интервальная; нечеткая;
решения
статистическая
Управление; прогнозирование; измерение;
Область применения
контроль; диагностирование:
решения
проектирование; классификация
39

40.

• В общем случае задача принятия решения представима кортежем
следующего вида:
• Множество альтернатив зависит от имеющейся базы знаний,
новизны задачи, типа проблемной ситуации.
• Метод получения решения зависит от имеющейся информации
о задаче и включает способ выбора альтернатив, определяемый
структурой предпочтений ЛПР, и метод принятия решений,
обусловливающий способ агрегирования критериев. В частности,
способ выбора альтернатив может предусматривать поиск
наилучшего решения, удовлетворительного решения, наиболее
предпочтительной альтернативы, эффективной (недоминируемой)
альтернативы, возможной альтернативы, наиболее типичной
альтернативы и т.п.

41. Модели принятия решений

41

42. Однокритериальный выбор

Задача однокритериального выбора является достаточно простой в
случае если:
1. Выбор любой альтернативы приводит к однозначно известным
последствиям (выбор в условиях определенности).
2. Параметры альтернативы (x) и функция предпочтения q(x) известны
и количественно определимы.
3. Критерий выбора единственен.
К сожалению данные условия на практике встречаются очень редко.
Многокритериальный выбор
• Многокритериальные задачи не имеют однозначного общего
решения.
Поэтому
предлагается
много
способов
придать
многокритериальной задаче частный вид, допускающий единственное
общее решение. Естественно, что для разных способов эти решения
являются в общем случае различными. Поэтому едва ли не главное в
решении многокритериальной задачи – обоснование данного вида ее
42
постановки.

43.

Используются различные варианты упрощения
многокритериальной задачи выбора. Перечислим некоторые из них:
1. Сведение многокритериальной задачи к однокритериальной, путем
ввода суперкритерия.
2. Условная максимизация (находится не глобальный экстремум
суперкритерия, а локальный экстремум основного критерия).
3. Поиск альтернативы с заданными свойствами.
4. Нахождение множества Парето.
43

44. Модели оптимизации

45.

Аддитивная свертка (от англ. addition – сложение).
Аддитивная
свертка
наиболее
приемлема
для
критериев,
представляющих собой однородные по смыслу и близкие по масштабу
значений величины.
Низкие оценки по одним критериям могут компенсироваться высокими
оценками по другим критериям. Это значит, что уменьшение одного из
критериев вплоть до нулевого значения может возмещаться возрастанием
другого.
Мультипликативная свертка (от англ. multiplication – умножение).
Достоинством мультипликативного критерия является то, что при его
использовании не требуется нормировки частных критериев. К его
недостаткам относится то, что он компенсирует недостаточную величину
одного частного критерия избыточной величиной другого и имеет тенденцию
сглаживать уровни частных критериев за счет неравнозначных
первоначальных значений частных критериев.
Максминная свертка (выбор по наихудшему критерию).
Эта свертка учитывает критерий, имеющий наименьшее значение. Иногда
при ее применении полагают, что веса критериев близки друг к другу, либо
все критерии имеют одинаковую важность.

46.

Построение множества Парето. Наряду с методами первой группы,
использующими свертку в пространстве критериев, применяются методы
второй группы, основанные на сужении множества альтернатив, в которых
пытаются уменьшить число возможных вариантов решений, исключив
заведомо плохие. Один из подходов, обладающий большой общностью, был
предложен итальянским экономистом В.Парето в 1904 г. и называется
методом, основанным на принципе Парето или, коротко, методом Парето.
Он применяется, когда число альтернатив велико и альтернативы имеют
противоречивые оценки по разным критериям. В этом случае применение
методов первой группы может привести к ненадежным решениям и
необходим неформальный анализ множества альтернатив.
Он позволяет сузить исходное множество альтернатив, причем
окончательный выбор остается за ЛПР. Альтернативы, входящие в
множество Парето, попарно не сравнимы друг с другом, т.е. по одним
критериям лучше одна альтернатива, по другим другая и т.д., и их
невозможно улучшить одновременно по всем критериям. Поэтому анализ
множества Парето позволяет найти компромисс между противоречивыми
требованиями и дает ЛПР возможность судить о том, какова “цена”
увеличения одного из критериев и как это скажется на ухудшении остальных.
Построение множества Парето является необходимым при решении
многокритериальных задач выбора в системах (управление, проектирование
промышленных и транспортных объектов и т.п.).
46

47.

Пусть имеется учебная группа (множество альтернатив), требуется
выбрать наилучшего студента (альтернативу) по ряду критериев, например
сообразительность, успеваемость, манера поведения, внешний вид,
умение выражать свои мысли и т.п. Предположим, что студент 1 x – самый
сообразительный, а по остальным критериям не выделяется.
Студенты 2 x , 3 x , 4 x , 5 x имеют высокие значения остальных
критериев, так, что они в среднем превосходят 1 x , причем 2 x лучше всех
по успеваемости, а по остальным критериям не хуже других студентов.
Тогда 1 x обязательно попадает в множество Парето, так как он
уникальный (единственный) по первому критерию, а от группы студентов 2
x … 5 x в Парето попадает один представитель – 2 x , хотя остальные
студенты превосходят 1 x по нескольким критериям (число критериев здесь
не имеет значения).
После того, как построено множество Парето, для определения
наилучшего решения из оставшихся применяются в зависимости от
условий задачи методы первой группы: метод свертки, метод главного
критерия и т.п. либо графические методы, например метод диаграмм.
47

48. Нахождение паретовского множества

• Метод состоит в попарном сравнении всех представленных
альтернатив
• Если предпочтение хотя бы по одному критерию расходится с
предпочтением по другому, то такие альтернативы признаются
несравнимыми.
• В результате попарного сравнения все худшие альтернативы
отбрасываются, а оставшиеся несравнимые между собой
принимаются.
• Если все максимально достижимые критерии не относятся к
одной альтернативе, то принятые альтернативы образуют
множество Парето.
• При необходимости выбрать одну альтернативу предлагается
вводить добавочные критерии или ограничения, бросать жребий
либо прибегать к услугам экспертов
48

49.

Подход, основанный на принципе равновесия (принципе Нэша).
Часто действия окружающей среды являются целенаправленными,
например, это имеет место для систем, включающих субъектов, причем
каждая
из
систем
стремится
достичь
своей
цели.
Случай
несогласованности целей субъектов называется конфликтом. Такая
ситуация характерна для теории игр.
При анализе конфликтов со многими субъектами одна из важных
проблем – это проблема коллективных решений, или компромисса. Для
принятия решений в таких системах сохраняет свое значение принцип
Парето. Эффективные альтернативы, принадлежащие множеству Парето,
обладают тем свойством, что улучшить значение целевой функции
(критерия) какого-либо субъекта можно только за счет других субъектов.
Наряду с принципом Парето широко используется принцип равновесия,
называемый также принципом устойчивости, или принципом Нэша. Этот
принцип позволяет сузить множество альтернатив, когда речь идет о
коллективном решении, принимаемом всеми взаимодействующими
субъектами по договоренности, при этом каждый поступается частью
своих интересов.
49

50.

Равновесное решение можно назвать устойчивым, так как если субъект
отступит от своего равновесного решения, т.е. выберет стратегию , то при
условии, что остальные субъекты сохранят свой выбор, он проиграет.
Принцип Нэша как раз и состоит в том, что наилучшие решения
принадлежат множеству равновесных решений. Однако следует отметить,
что равновесные решения в общем случае не являются эффективными и
наоборот.
Например, если решение принимается всеми субъектами независимо,
то их выбор вряд ли будет устойчивым. Кроме того, и при одновременном
решении часть субъектов может выбрать иное решение (например,
эффективное), что даст им преимущество перед остальными.
Таким образом, метод равновесия эффективен при сужении множества
альтернатив в закрытых системах, когда равновесные решения
одновременно принадлежат множеству Парето. Это бывает весьма редко,
так как большинство систем являются открытыми и для них эффективные
альтернативы являются неустойчивыми, а устойчивые – неэффективными.
50

51. Методы поиска решения

Методы решения задач, основанные на сведении их к поиску, зависят от
особенностей проблемной области, в которой решается задача, и от
требований ограничений, предъявляемых пользователем к решению.
Особенности проблемной области с точки зрения методов решения можно
характеризовать следующими параметрами:
1) размер;
2) изменяемость области;
3) полнота модели, описывающей область;
4) определенность данных о решаемой задаче.
Параметр "размер" характеризует размер пространства, в котором
предстоит искать решение.
Параметр "изменяемость" характеризует степень изменяемости области
во времени и пространстве. По параметру "изменяемость« выделяют
статические и динамические области.
Параметр "полнота модели" характеризует адекватность модели,
используемой для описания данной проблемной области. Обычно, если
модель не полна, то для описания области используют несколько моделей,
дополняющих друг друга за счет отражения различных свойств проблемной
области (например, модель, описывающая электрическую схему двигателя, и
модель, определяющая его механическую схему).
51

52.

Параметр "определенность данных" характеризует степень точности
или ошибочности и полноты или неполноты данных.
"Точность" является показателем того, что проблемная область с точки
зрения решаемых задач описана точными данными.
"Ошибочность" является показателем того, что данные о проблемной
области не точны.
Под "полнотой" (неполнотой) данных понимается достаточность
(недостаточность) входных данных для однозначного решения задачи.
Обычно при неполноте данных для поиска решения необходимо
использовать некоторые предположения или ограничения.
Требования пользователя к результату задачи, решаемой с помощью
поиска, можно характеризовать "количеством решений" и свойствами
результата" (и/или способом его получения). Параметр "количество решений"
может принимать следующие основные значения:
• одно решение,
• несколько решений,
• все решения.
Параметр
"свойства"
задает
ограничения,
которым
должен
удовлетворять полученный результат или способ его получения. Так,
например, для системы, выдающей рекомендации по лечению больных,
пользователь может указать требование не использовать некоторое
лекарство (в связи с его отсутствием или в связи с тем, что оно
52
противопоказано данному пациенту).

53.

Параметр "свойства" может определять и такие особенности, как время
решения ("не более чем", "диапазон времени" и т.п.), объем памяти,
используемой для получения результата, указание об обязательности
(невозможности) использования каких-либо знаний (данных) и т.п.
Сложность задачи можно характеризовать примерно следующим
набором параметров:
1) размер пространства, в котором решается задача;
2) изменяемость области;
3) полнота модели;
4) определенность данных;
5) количество необходимых решений;
6) ограничения на результат и способ его получения.
Сложность задачи колеблется от простых задач (малая область,
статическая область, полная модель, определенные данные, какое-нибудь
решение, отсутствие ограничений на результат и способ его получения) до
сложных задач (большая область, динамическая область, неполнота одной
модели, ошибочные и неполные данные, все решения, произвольные
ограничения на результат и способ его получения).
Одним методом нельзя решить все задачи. Обычно одни методы
превосходят другие только по некоторым из перечисленных параметров.
53

54.

Существующие методы решения задач, используемые в экспертных
системах, можно классифицировать следующим образом:
1. Методы поиска в одном пространстве - методы, предназначенные для
использования в следующих условиях: малые области, статические области,
полнота модели, точные и полные данные.
2. Методы поиска в иерархических пространствах - методы,
предназначенные для работы в больших статических областях.
3. Методы поиска при неточных и неполных данных.
4. Методы поиска в динамической проблемной области - методы,
предназначенные для работы с областями, изменяемыми во времени и (или)
в пространстве.
5. Методы поиска, использующие несколько моделей, предназначенные
для работы с областями, для адекватного описания которых одной модели
недостаточно.
Предполагается, что перечисленные методы при необходимости должны
объединяться для того, чтобы позволить решать задачи, сложность которых
возрастает одновременно по нескольким из перечисленных выше параметров.
54

55.

• В криптографии на вычислительной сложности полного перебора
основывается оценка криптостойкости шифров. В частности, шифр считается
криптостойким, если не существует метода «взлома» существенно более
быстрого чем полный перебор всех ключей. Криптографические атаки,
основанные на методе полного перебора, являются самыми универсальными,
но и самыми долгими.
• Полный перебор (или метод «грубой силы», англ. brute force) — метод
решения математических задач. Относится к классу методов поиска решения
исчерпыванием всевозможных вариантов. Сложность полного перебора
зависит от количества всех возможных решений задачи. Если пространство
решений очень велико, то полный перебор может не дать результатов в
течение нескольких лет или даже столетий.
55

56. Множественность задач выбора

Ситуация выбора может реализовываться в различных вариантах.
Отметим основные из них:
• Множество альтернатив может быть конечным, счетным или
континуальным
• Оценка альтернативы может осуществляться по одному или
нескольким критериям, которые могут иметь как количественный, так и
качественный характер
• Режим выбора может быть однократным или повторяющимся
• Последствия выбора могут быть точно известны (выбор в условиях
определенности), иметь вероятностный характер (выбор в условиях
риска),
иметь
неоднозначный
исход
(выбор
в
условиях
неопределенности)
• Ответственность за выбор может быть односторонней
или
многосторонней
• Степень согласованности целей при многостороннем выборе может
варьироваться от полного совпадения целей (кооперативный выбор) до
их противоположности (выбор в конфликтной ситуации). Возможны
промежуточные случаи (компромиссный выбор, коалиционный выбор,
выбор в условиях нарастающего конфликта)
56

57. Критериальный язык описания выбора

• Название
этого
языка
связано
с
основным
предположением, состоящим в том, что каждую отдельно
взятую альтернативу можно оценить некоторым конкретным
(одним) числом, после чего сравнение альтернатив сводится
к сравнению соответствующих им чисел.
• Пусть, например, {X} – множество альтернатив, а x –
некоторая определенная альтернатива, принадлежащая этому
множеству.
• Тогда считается, что для всех x может быть задана
функция: q(x), которая называется критерием (критерием
качества, целевой функцией, функцией предпочтения,
функцией полезности и т.п.), обладающая тем свойством, что
если альтернатива x1 предпочтительнее x2: (обозначается: x1
> x2), то: q(x1) > q(x2).
• При этом выбор сводится к отысканию альтернативы с
наибольшим значением критериальной функции.
57

58. Сведение многокритериальной задачи к однокритериальной

• Введем суперкритерий q0(x), как скалярную функцию векторного
аргумента:
q0(x)= q0((q1(x), q2(x),…, qn(x)).
• Суперкритерий позволяет упорядочить альтернативы по величине q0,
выделив тем самым наилучшую (в смысле этого критерия). Вид функции
q0 определяется тем, как конкретно мы представляем себе вклад каждого
критерия в суперкритерий. Рассмотрим функцию:
q0=Сумма(ai*qi/si)
• Коэффициенты si обеспечивают:
1. безразмерность или единую размерность числа ai*qi/si (различные
частные критерии могут иметь разную размерность, и тогда над ними
нельзя производить арифметических операций и свести их в
суперкритерий);
2. нормировку, т.е. обеспечение условия: ai*qi/si<1.
• Коэффициент ai отражает относительный вклад частных критериев qi
в суперкритерий (весовой коэффициент).
• Итак, в многокритериальной постановке задача принятия решения о
выборе одной из альтернатив сводится к максимизации суперкритерия 58

59. Выбор весовых коэффициентов

Основная проблема в многокритериальной постановке
задачи принятия решений состоит в том, что необходимо
найти такой аналитический вид коэффициентов ai, который
бы обеспечил следующие свойства модели:
1. высокую степень адекватности предметной области и
точке зрения экспертов;
2. минимальные вычислительные трудности максимизации
суперкритерия, т.е. его расчета для разных альтернатив;
3. устойчивость результатов максимизации суперкритерия
от малых возмущений исходных данных.
Устойчивость решения означает, что малое изменение
исходных данных должно приводить к малому изменению
величины суперкритерия, и, соответственно, к малому
изменению принимаемого решения. То есть практически на
тех же исходных данных должно приниматься или тоже
самое, или очень близкое решение.
59

60. Условная максимизация

• Данный метод использует факт, что частные критерии обычно
неравнозначны между собой
• Метод состоит в выделении одного основного критерия, при этом
остальные критерии задаются диапазонами значений и играют роль
ограничителей
• Основной задачей является нахождение условного экстремума
основного критерия в приемлемых диапазонах остальных критериев
Поиск альтернативы с заданными
свойствами
• Применим в случае, когда заранее могут быть указаны значения частных
критериев (или их границы)
• Задача состоит в:
– Поиске альтернативы, удовлетворяющей этим требованиям или
установлении факта отсутствия данной альтернативы
– Поиске альтернативы, которая подходит к поставленным целям
ближе всего
60

61. Метод анализа иерархий (МАИ)

Часто используемый в последнее время метод принятия решений МАИ, опирающийся на многокритериальное описание проблемы, был
предложен и детально описан Саати Т.
В методе используется дерево критериев, в котором общие критерии
разделяются на критерии частного характера. Для каждой группы критериев
определяются коэффициенты важности.
Альтернативы также сравниваются между собой по отдельным
критериям с целью определения каждой из них.
Средством определения коэффициентов важности критериев либо
критериальной ценности альтернатив является попарное сравнение.
Результат сравнения оценивается по бальной шкале. На основе таких
сравнений вычисляются коэффициенты важности критериев, оценки
альтернатив и находится общая оценка как взвешенная сумма оценок
критериев.
В ходе детального исследования МАИ были выявлены следующие
существенные недостатки, такие как:
–
Рассогласование оценок, связанное с трудностями оценки отношений
сложных элементов - 1-й вид рассогласования.
–
Рассогласование 2-го вида, связанное с предложенной дискретной
шкалой для оценки элементов.
–
Резкое увеличение количества оценок с увеличением набора элементов.
61
Не рекомендуется набор элементов больше 9.

62. Групповой выбор

• Пусть имеется группа лиц, имеющих право принимать участие в
коллективном принятии решений.
• Предположим, что эта группа рассматривает некоторый набор
альтернатив, и каждый член группы осуществляет свой выбор.
• Ставится задача о выработке решения, которое определенным
образом согласует индивидуальные выборы и в каком-то смысле
выражает “общее мнение” группы, т.е. принимается за групповой
выбор.
• Естественно, различным принципам согласования индивидуальных
решений будут соответствовать различные групповые решения.
62

63. Правила голосования

• Правила согласования индивидуальных решений при групповом
выборе называются правилами голосования.
• Наиболее распространенным является “правило большинства”, при
котором за групповое решение принимается альтернатива, получившая
наибольшее число голосов.
• Необходимо понимать, что такое решение отражает лишь
распространенность различных точек зрения в группе, а не
действительно оптимальный вариант, за который вообще никто может и
не проголосовать. “Истина не определяется путем голосования”.
• Кроме того, существуют так называемые “парадоксы голосования”,
наиболее известный из которых парадокс Эрроу.
• Эти парадоксы могут привести, и иногда действительно приводят, к
очень неприятным особенностям процедуры голосования: например
бывают случаи, когда группа вообще не может принять единственного
решения (нет кворума или каждый голосует за свой уникальный вариант,
и т.д.), а иногда (при многоступенчатом голосовании) меньшинство
может навязать свою волю большинству.
63

64. Экспертные методы выбора

• При исследовании сложных систем часто возникают проблемы, которые по
различным причинам не могут быть строго поставлены и решены с
применением разработанного в настоящее время математического
аппарата. В этих случаях прибегают к услугам экспертов (системных
аналитиков), чей опыт и интуиция помогают уменьшить сложность
проблемы.
• Однако, необходимо учитывать, что эксперты сами представляют собой
сверхсложные системы, и их деятельность сама зависит от многих
внешних и внутренних условий. Поэтому в методиках организации
экспертных оценок большое внимание уделяется созданию благоприятных
внешних и психологических условий для работы экспертов.
• Взаимодействие между экспертами может как стимулировать, так и
подавлять их деятельность. Поэтому в разных случаях используют
различные методы экспертизы, отличающиеся характером взаимодействия
экспертов друг с другом: анонимные и открытые опросы и анкетирования,
совещания, дискуссии и т.д.
• Существуют различные методы математической обработки мнений
экспертов. Экспертам предлагают оценить различные альтернативы либо
одним, либо системой показателей. Кроме того им предлагают оценить
степень важности каждого показателя (его “вес” или “вклад”). Самим
экспертам
также
приписывается
уровень
компетентности,
соответствующий его вкладу в результирующее мнение группы.
64

65. Метод «Делфи»

Метод Дельфи представляет собой многотуровую процедуру
анкетирования с обработкой и сообщением результатов каждого тура
экспертам, работающим отдельно друг от друга.
Этот метод был разработан Хелмером и Гордоном (США) в середине
50-х годов для составления всевозможных прогнозов.
Особенностью метода является то, что какие-либо дискуссии между
экспертами запрещены, что, по мнению авторов метода, исключает роль
психологических и эмоциональных факторов, неизбежно проявляющихся во
время открытой дискуссии.
Итеративная процедура опроса с сообщением результатов обработки
после каждого тура обеспечивает лучшее согласование мнений экспертов,
поскольку эксперты, давшие сильно отклоняющиеся оценки, вынуждены
критически осмыслить свои суждения и обстоятельно их аргументировать.
Необходимость аргументации или корректировки своих оценок не
означает, что целью экспертизы является получение полной согласованности
мнений экспертов.
Конечным результатом может оказаться выявление двух или более
групп мнений, отражающих принадлежность экспертов к различным
научным школам, ведомствам или категориям лиц. Получение такого
результата является также полезным, поскольку позволяет выяснить наличие
различных точек зрения и поставить задачу проведения исследований в
данной области.
65

66. Этапы метода «Делфи»

• Экспертам предлагается ответить на ряд вопросов и свои ответы
аргументировать.
• Полученные от эксперта данные обрабатываются с целью выделения
среднего или медианы и крайних значений оценок.
• Экспертам сообщаются результаты обработки первого тура опроса с
указанием расположения оценок каждого эксперта. Если оценка эксперта
сильно отклоняется от среднего значения, то его просят аргументировать
свое мнение или изменить оценку.
• Во втором туре эксперты аргументируют или изменяют свою оценку
с объяснением причин корректировки. Результаты опроса во втором туре
обрабатываются и сообщаются экспертам. Если после первого тура
производилась корректировка оценок, то результаты обработки второго
тура содержат новые средние и крайние значения оценок экспертов.
• Далее процедура повторяется
• Обычно после третьего или четвертого тура оценки экспертов
стабилизируются, что и служит критерием прекращения дальнейшего
опроса.
66

67. Функционально-стоимостной анализ

• Автором метода функционально-стоимостного анализа является Майлз.
Цель метода - ускорить поиск путей снижения себестоимости изделия в
проектных и производственных организациях.
• Данный метод включает следующие этапы:
• 1. Организовать бригаду по функционально-стоимостному анализу, в
которую включают консультанта по методу и представителей всех
различных служб.
• 2. Сформулировать функцию всего изделия и определить требования по
параметрам изделия.
• 3.
Составить
подробную
калькуляцию
себестоимости
всех
технологических операций по производству изделия, включающую расходы
на приобретение материалов и комплектующих.
• 4. По каждой детали изделия комплексная бригада выполняет
следующие шаги:
определяет все функции детали;
• составляет перечень цен самых дешевых из всех известных устройств,
способных выполнять эти функции и получает суммарную цену выполнения
всех функций, представляющую нижнюю границу цены детали;
• выбирает функционально совместимые устройства наиболее низкой
стоимости
• оформляет изменения исходного изделия.
• 5. Представить результаты стоимостного анализа на одобрение
консультантам по функционально-стоимостному анализу, конструкторскому
67
бюро, администрации.

68. Метод «за – против»

Каждой представленной
альтернативе «прикрепляют» по 2
представителя концепции «за» (защитники) и столько же «против» (критики)
Этапы выбора:
1. Представители концепции «за» и «против» получают слово и в сжатом
виде приводят свои аргументы, которые фиксируются жюри на «табло
доводов» (продолжительность 10-15 минут)
2. Представители концепции «за» и «против» меняются ролями и приводят
дополнительные доводы
3. Жюри обсуждает все доводы и при необходимости их дополняет и
выбирает лучшие
4. Жюри дробиться на группы по 4-6 человек, задачей которых является
независимая обработка и совершенствование принятых вариантов
68

69. Эвристические методы

• К эвристическим методам относят следующие методы:
– метод взвешенной суммы оценок критериев.
• Каждой альтернативе дается числовая (бальная) оценка по каждому из
критериев.
Критериям
приписывается
количественные
веса,
характеризующие их сравнительную важность. Веса умножаются на
критериальные оценки, полученные числа суммируются - так определяется
ценность альтернативы. Далее выбирается альтернатива с наибольшим
показателем ценности.
– метод компенсации.
• Данный метод используется при попарном сравнении альтернатив.
• Достоинством всех эвристических методов является простота и
удобство, а основным недостатком то, что все они не имеют научного
обоснования.
• Таким образом, проведенный анализ показал, что рассмотренные
методы, положенные в основу теории принятия решения, носят
аксиоматический и эвристический характер, т.е. не имеют строгого научного
доказательства.
• Данные методы не позволяют интеллектуализировать процесс принятия
решения, так как выработка окончательного решения всегда остается за ЛПР.
Поэтому,
предложен
подход,
ориентированный
на
методы
интеллектуального анализа данных, необходимых ЛПР в процессе принятия
решения.
69

70. Выбор в условиях неопределенности

Выбор в условиях определенности – это частный случай выбора в
условиях неопределенности (когда неопределенность близка к нулю).
Но неопределенность чего конкретно имеется в виду?
В современной теории выбора считается, что в задачах принятия решений
существует три основных вида неопределенности:
1. информационная (статистическая) неопределенность исходных данных
для принятия решений;
2. неопределенность последствий принятия решений (выбора);
3. расплывчатость в описании компонент процесса принятия решений.
70

71. Выбор в условиях статистической неопределенности

Данные, полученные о предметной области, не могут рассматриваться
как абсолютно точные.
Эти данные нас интересуют не сами по себе, а лишь в качестве
сигналов, которые, возможно, несут определенную информацию о том,
что нас в действительности интересует.
То есть, реалистичнее считать, что мы имеем дело с данными, не
только зашумленными и неточными, но еще и косвенными, а возможно и
не полными.
В этих условиях используется теория статистических решений.
В
этой
теории
существует
два
основных
источника
неопределенности.
– неизвестно, какому распределению подчиняются исходные данные.
– неизвестно, какое распределение имеет то множество (генеральная
совокупность), о котором мы хотим сделать выводы по его
подмножеству, образующему исходные данные.
Статистические процедуры это и есть процедуры принятия решений,
снимающих оба эти виды неопределенности.
71

72. Причины некорректного применения теории статистических решений

Необходимо отметить, что существует ряд причин, которые приводят
к некорректному применению статистических методов:
1. статистические выводы, как и любые другие, всегда имеют
некоторую определенную надежность или достоверность. Но, в отличие
от многих других случаев, достоверность статистических выводов
известна и определяется в ходе статистического исследования;
2. качество решения, полученного в результате применения
статистической процедуры зависит, от качества исходных данных;
3. не следует подвергать статистической обработке данные, не имеющие
статистической природы
72

73. Неопределенность последствий

• Когда последствия выбора той или иной альтернативы однозначно
определяются самой альтернативой, тогда можно не различать альтернативу
и ее последствия, считая само собой разумеющимся, что выбирая
альтернативу мы в действительности выбираем ее последствия.
• Однако, в реальной практике нередко приходится иметь дело с более
сложной ситуацией, когда выбор той или иной альтернативы неоднозначно
определяет последствия сделанного выбора.
• В случае дискретного набора альтернатив и исходов их выбора, при
условии, что сам набор возможных исходов общий для всех альтернатив,
можно считать, что различные альтернативы отличаются друг от друга
распределением вероятностей исходов. Эти распределения вероятностей
вообще говоря могут зависеть от результатов выбора альтернатив и реально
наступивших в результате этого исходов. В простейшем случае исходы
равновероятны. Сами исходы обычно имеют смысл выигрышей или потерь и
выражаются количественно.
• Если исходы равны для всех альтернатив, то выбирать нечего. Если же
они различны, то можно сравнивать альтернативы, вводя для них те или
иные количественные оценки. Разнообразие задач теории игр связано с
различным выбором числовых характеристик потерь и выигрышей в
результате выбора альтернатив, различными степенями конфликтности
между сторонами, выбирающими альтернативы и т.д.
73

74. Выбор при расплывчатой неопределенности

• Любая задача выбора является задачей целевого сужения множества
альтернатив. Как формальное описание альтернатив (сам их перечень,
перечень их признаков или параметров), так и описание правил их
сравнения (критериев, отношений) всегда даются в терминах той или иной
измерительной шкалы (даже тогда, когда тот, кто это делает, не знает об
этом).
• Известно, все шкалы размыты, но в разной степени. Под термином
“размытие” понимается свойство шкал, состоящее в том, что всегда можно
предъявить такие две альтернативы, которые различимы, т.е. различны в
одной шкале и неразличимы, т.е. тождественны в другой – более размытой.
Чем меньше градаций в некоторой шкале, тем более она размыта.
• Таким образом, мы можем четко видеть альтернативы, и одновременно
нечетко их классифицировать, т.е. иметь неопределенность в вопросе о том,
к каким классам они относятся. Уже в первой работе по принятию решений
в расплывчатой ситуации Беллман и Заде выдвинули идею, состоящую в
том, что и цели, и ограничения должны представляться как размытые
(нечеткие) множества на множестве альтернатив.
74

75. Недостатки оптимизационного подхода

• Во всех рассмотренных выше задачах выбора и методах
принятия решений проблема состояла в том, чтобы в исходном
множестве найти наилучшие в заданных условиях, т.е.
оптимальные в определенном смысле альтернативы.
• Идея
оптимальности
является
центральной
идеей
кибернетики и прочно вошла в практику проектирования и
эксплуатации технических систем. Вместе с тем эта идея
требует осторожного к себе отношения, когда мы пытаемся
перенести ее в область управления сложными, большими и
слабо детерминированными системами, такими, например, как
социально-экономические системы.
• Итак, идею оптимальности, чрезвычайно плодотворную для
систем,
поддающихся
адекватной
математической
формализации, нельзя перенести на сложные системы.
75

76. Недостатки оптимизационного подхода

• Конечно, математические модели, которые удается иногда
предложить для таких систем, можно оптимизировать. Однако
всегда следует учитывать сильную упрощенность этих моделей,
а также то, что степень их адекватности фактически неизвестна.
• Поэтому не известно, какое чисто практическое значение
имеет эта оптимизация. Высокая практичность оптимизации в
технических системах не должна порождать иллюзий, что она
будет настолько же эффективна при оптимизации сложных
систем. Содержательное математическое моделирование
сложных
систем
является
весьма
затруднительным,
приблизительным и неточным. Чем сложнее система, тем
осторожнее следует относится к идее ее оптимизации.
• Поэтому, при разработке методов управления сложными,
большими слабо детерминированными системами, авторы
считают основным не оптимальность выбранного подхода с
формальной математической точки зрения, а его адекватность
поставленной цели и самому характеру объекта управления.
76