Запроектировать кривую радиуса r

1.

Перед нами стоит задача запроектировать
кривую радиуса R. Рассмотрим этот вопрос...

2.

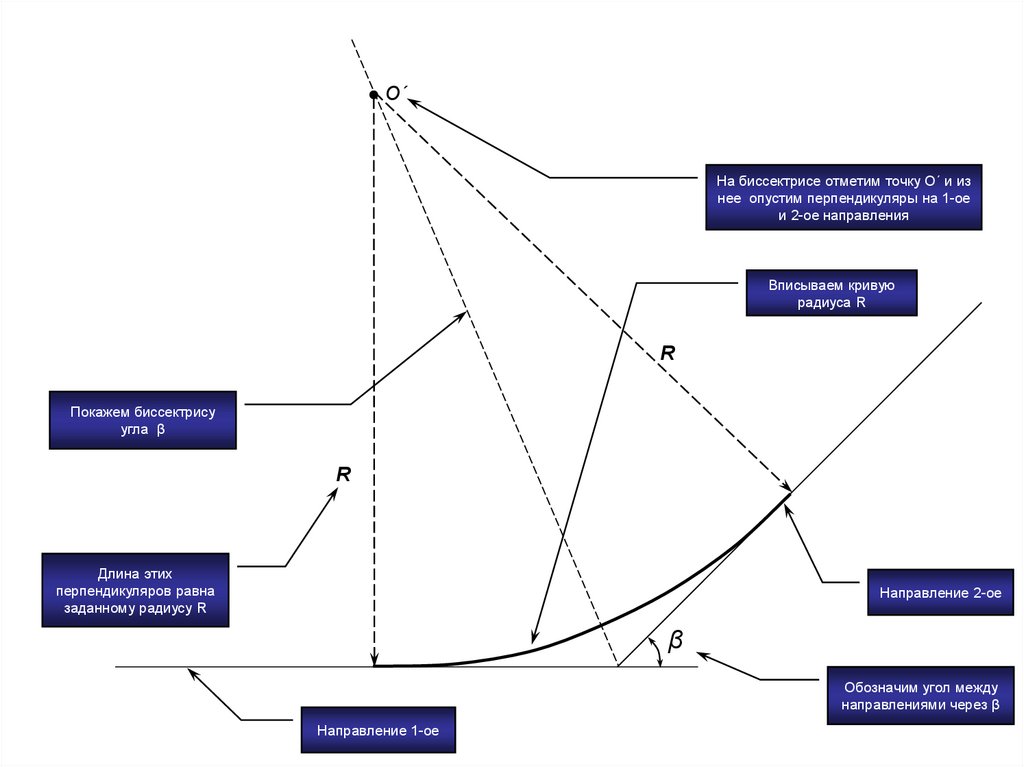
О´
На биссектрисе отметим точку О´ и из
нее опустим перпендикуляры на 1-ое
и 2-ое направления
Вписываем кривую
радиуса R
R
Покажем биссектрису
угла β
R
Длина этих
перпендикуляров равна
заданному радиусу R
Направление 2-ое
β
Обозначим угол между
направлениями через β
Направление 1-ое

3.

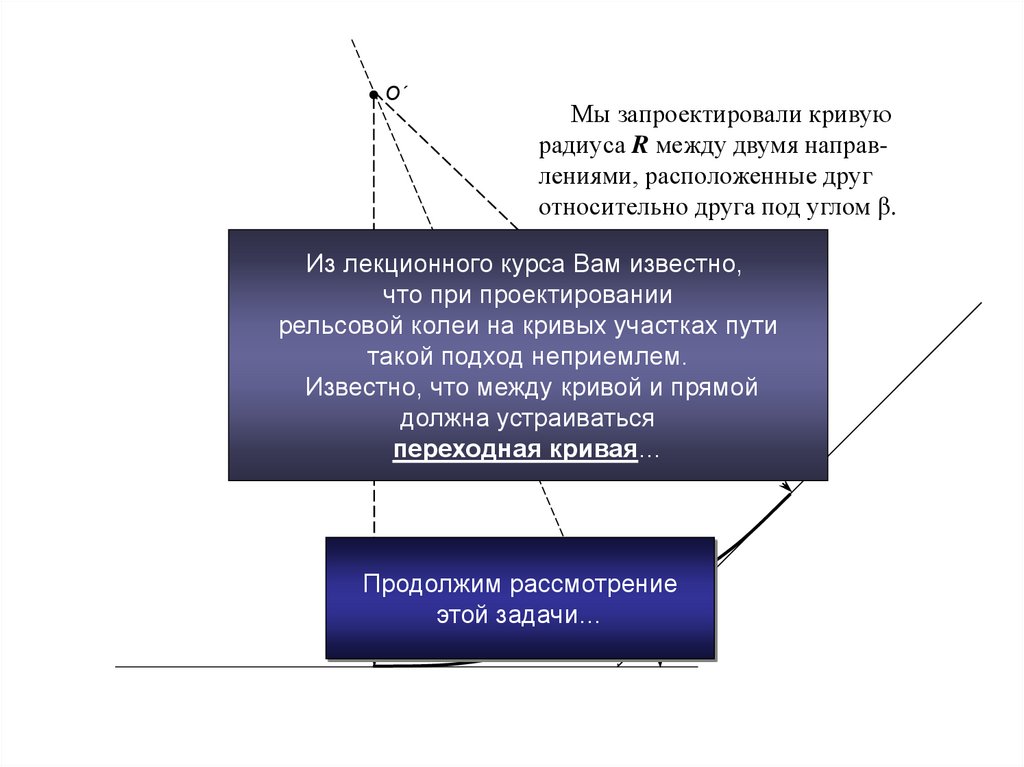
О´
Мы запроектировали кривую
радиуса R между двумя направлениями, расположенные друг
относительно друга под углом β.
Из лекционного курса Вам известно,
что при проектировании
рельсовой колеи на кривых участках пути
R
такой подход неприемлем.
Известно, что между кривой и прямой
должна устраиваться
переходная кривая…
R
Продолжим рассмотрение
этой задачи…
β

4.

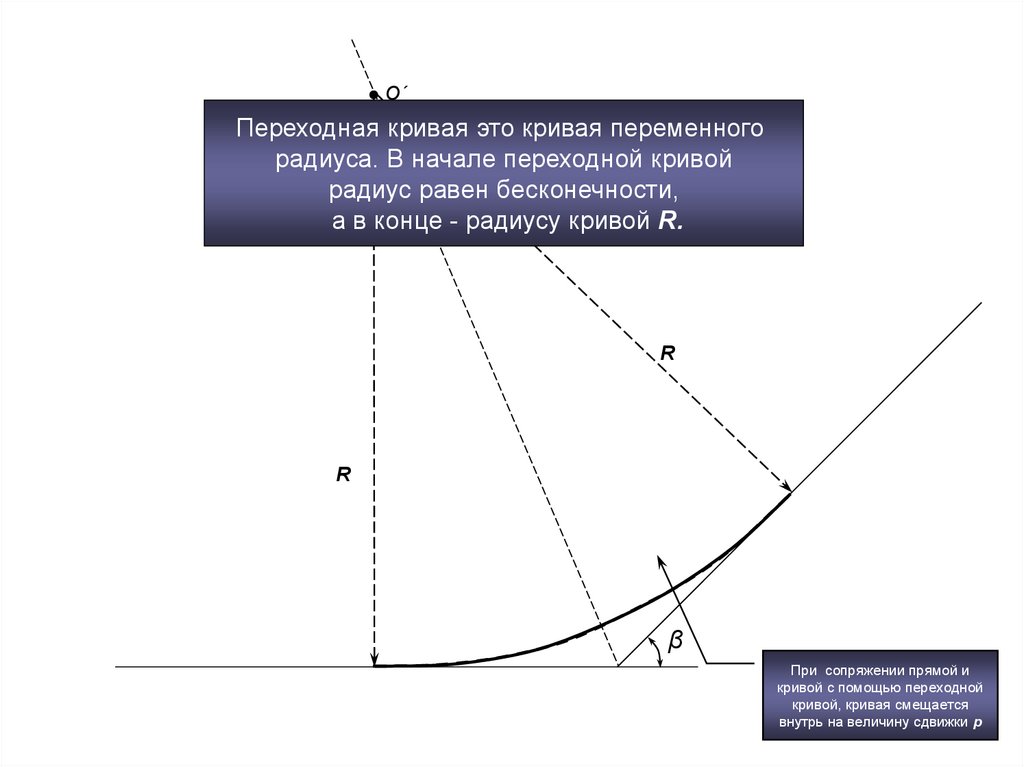
О´
Переходная кривая это кривая переменного
радиуса. В начале переходной кривой
радиус равен бесконечности,
а в конце - радиусу кривой R.
R
R
β
При сопряжении прямой и
кривой с помощью переходной
кривой, кривая смещается
внутрь на величину сдвижки p

5.

О”
P
О´
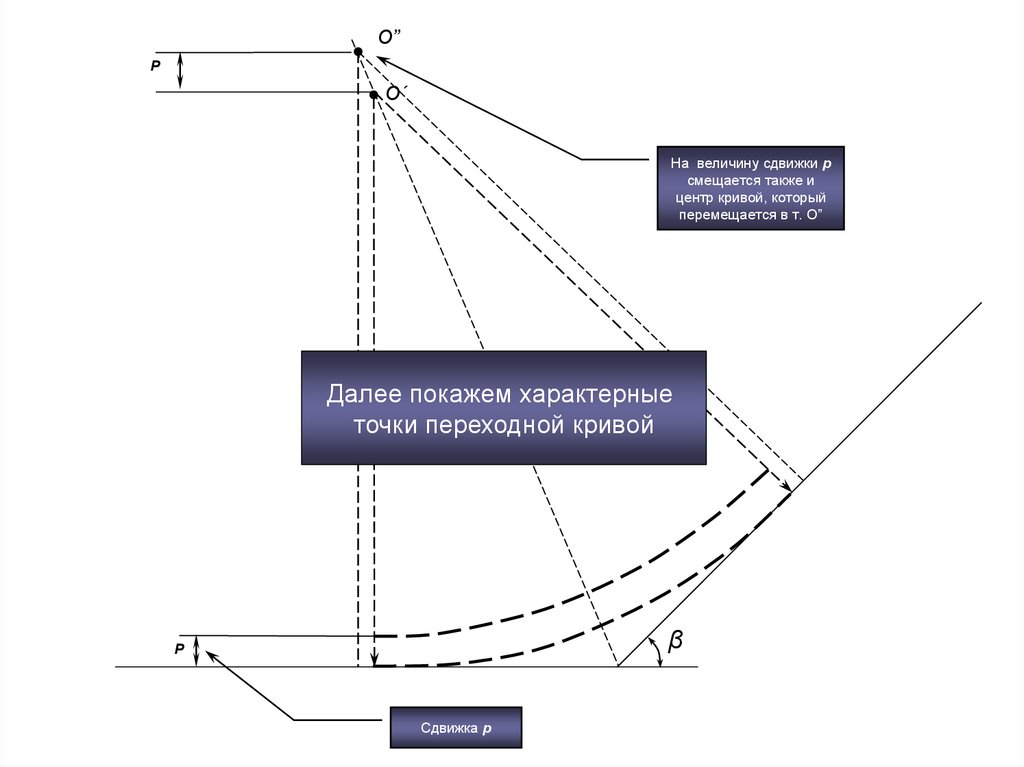
На величину сдвижки p
смещается также и
центр кривой, который
перемещается в т. О”
Далее покажем характерные
точки переходной кривой
β
P
Сдвижка p

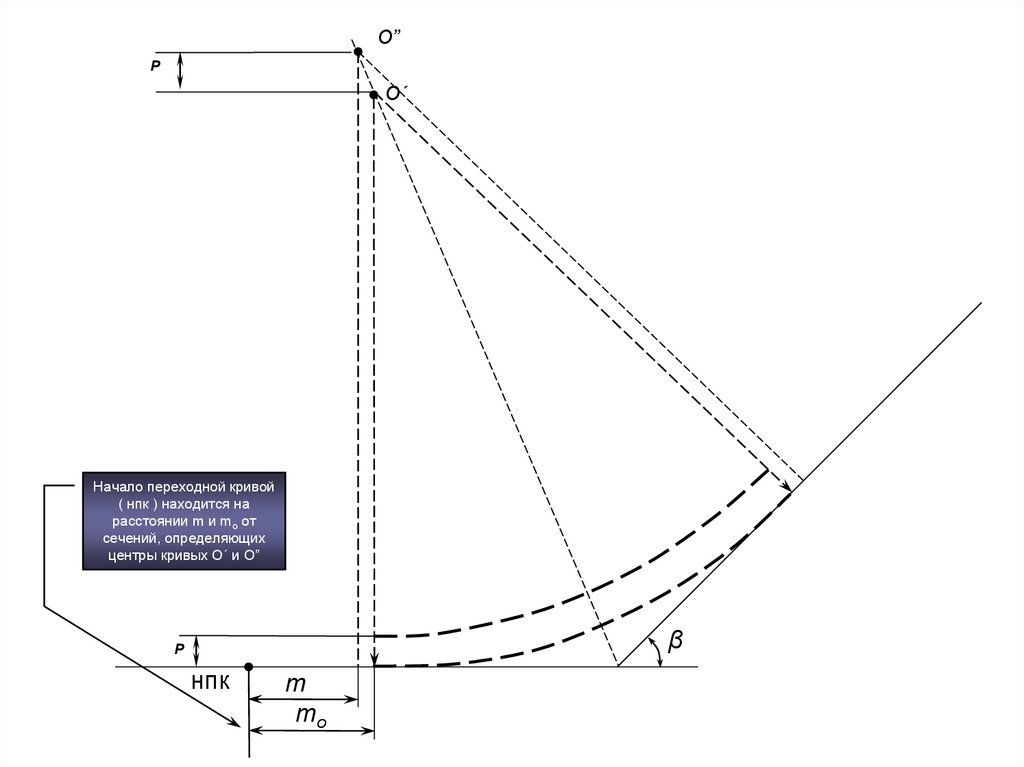
6.

О”
P
О´
Начало переходной кривой
( нпк ) находится на
расстоянии m и mо от
сечений, определяющих
центры кривых О´ и О”
β
P
нпк
m
mo

7.

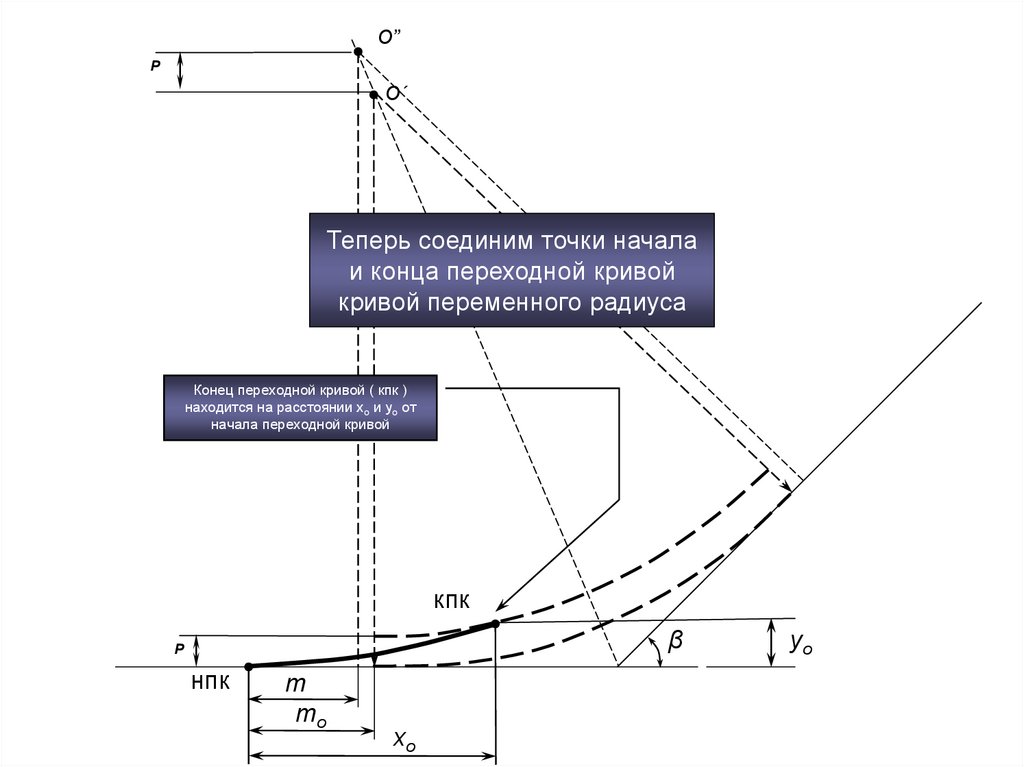
О”
P
О´
Теперь соединим точки начала
и конца переходной кривой
кривой переменного радиуса
Конец переходной кривой ( кпк )
находится на расстоянии хо и уо от
начала переходной кривой
кпк
β
P
нпк
m
mo
xо
yо

8.

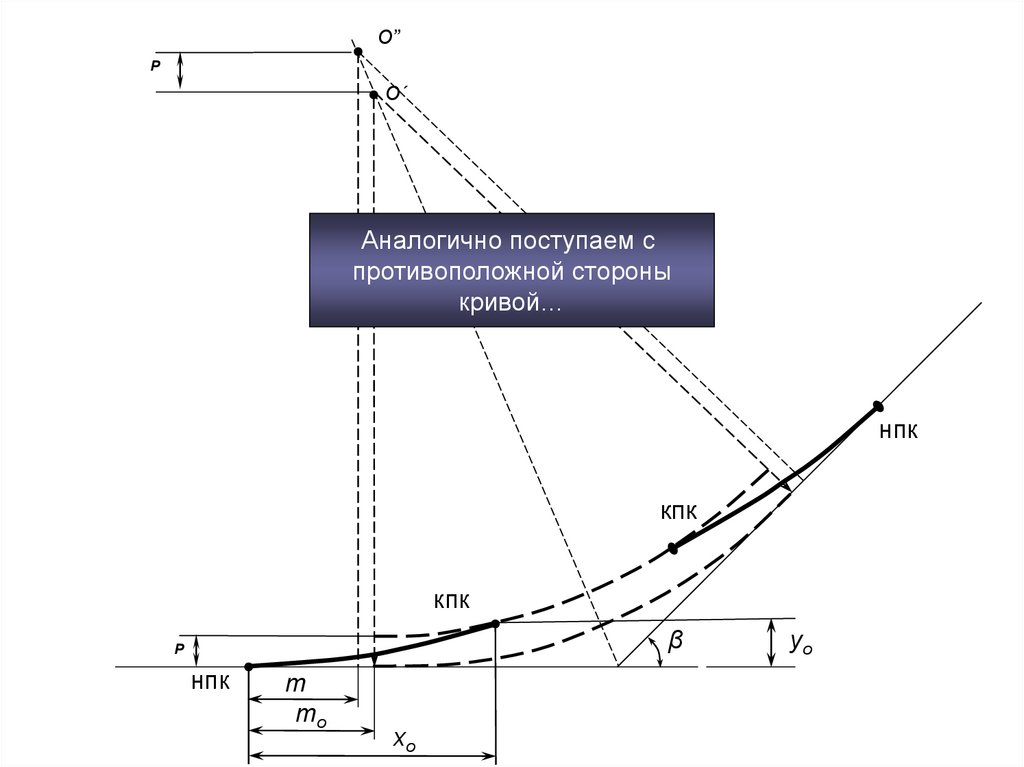
О”
P
О´
Аналогично поступаем с
противоположной стороны
кривой…
нпк
кпк
кпк
β
P
нпк
m
mo
xо
yо

9.

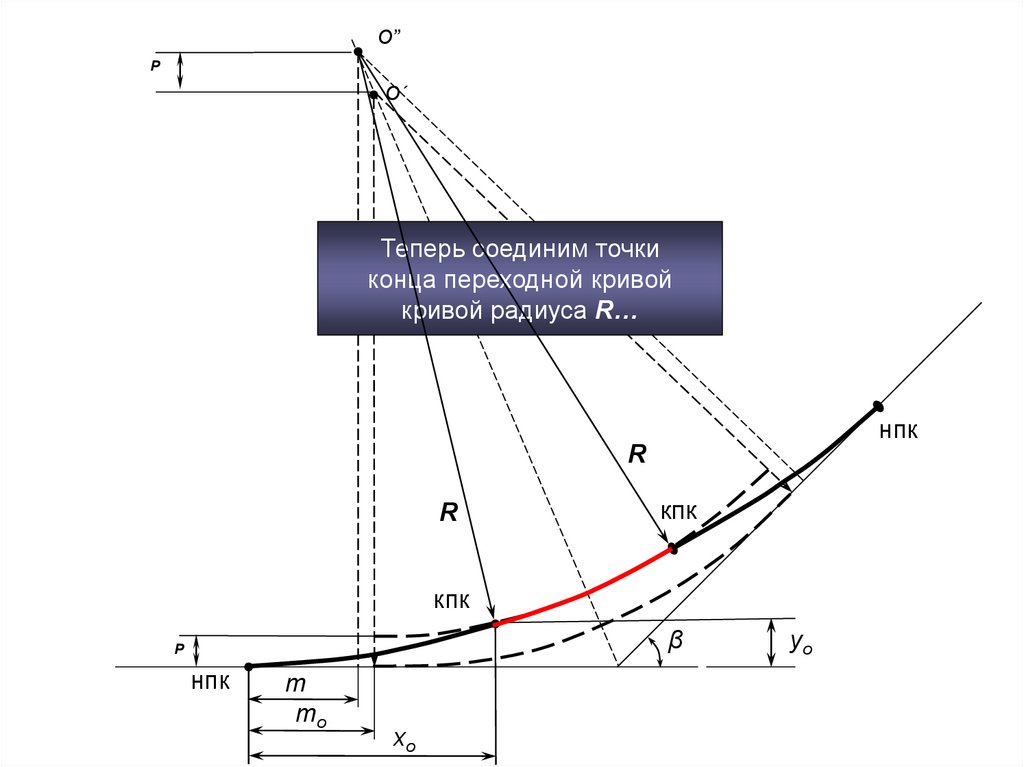
О”
P
О´
Теперь соединим точки
конца переходной кривой
кривой радиуса R…
нпк
R
R
кпк
кпк
β
P
нпк
m
mo
xо
yо

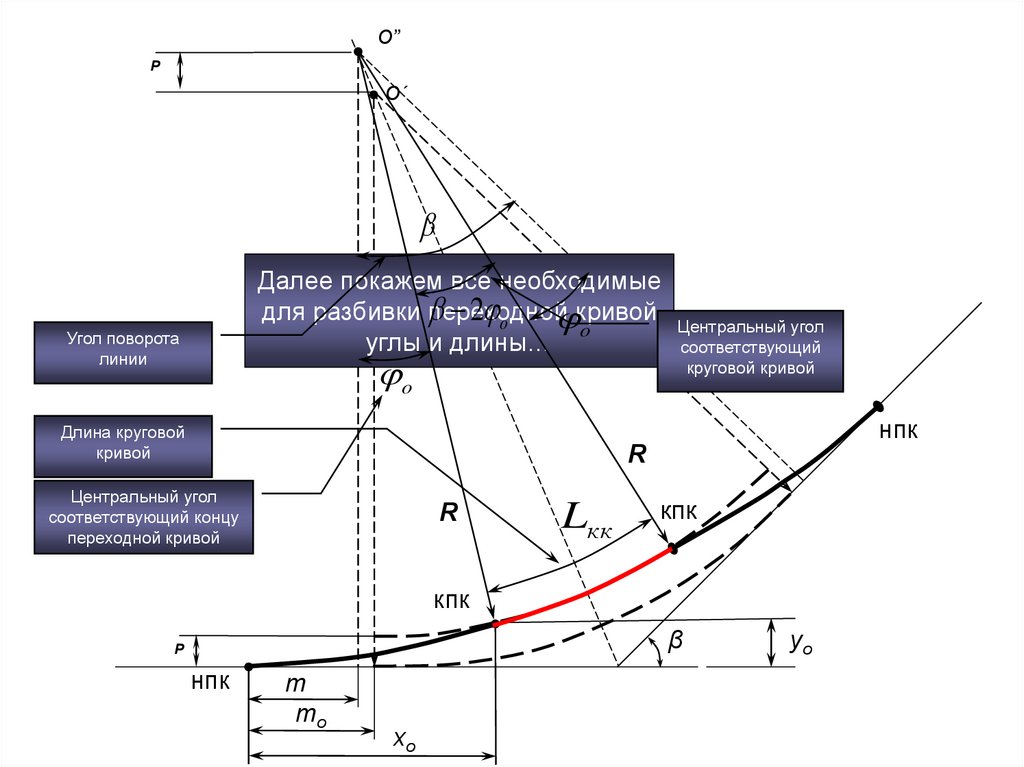
10.

О”
P
О´
Далее покажем все необходимые
2 o кривой
для разбивки
переходной
Центральный угол
o
углы и длины…
соответствующий
Угол поворота
линии
o
круговой кривой
нпк
Длина круговой
кривой
R
Центральный угол
соответствующий концу
переходной кривой
R
Lкк
кпк
кпк
β
P
нпк
m
mo
xо
yо

11.

О”
P
О´
Длина переходной
кривой
2 o
o
o
lo
Длина переходной
кривой
R
R
lo
Lкк
кпк
кпк
β
P
нпк
нпк
m
mo
xо
yо

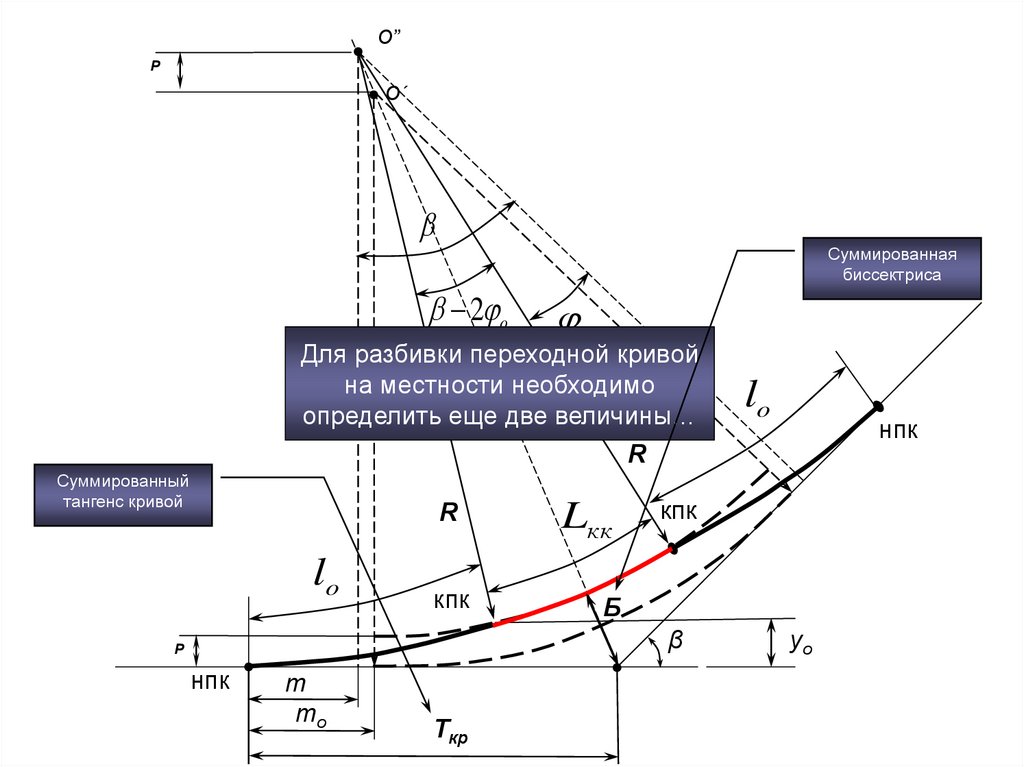
12.

О”
P
О´
Суммированная
биссектриса
2 o
o
Для разбивки переходной кривой
на
местности
необходимо
o
определить еще две величины…
R
Суммированный
тангенс кривой
lo
R
Lкк
кпк
Б
нпк
m
mo
Ткр
нпк
кпк
β
P
lo
yо

13.

Величины, которые были показаны на
рисунке определяются
по формулам…

14. Длина переходной кривой

h
lo
i
V,
Км/ч
40
50
55
60
65
70
75
80
85
90
100
110
120
140
i,‰
2,7
2,5
2,3
2,1
2,0
1,9
1,8
1,6
1,4
1,2
1,0
0,9
0,8
0,5
Проверяем условие:
lo
где
aнпVmax
0, 32Vmax
м
м
aнп 0, 7 2 ; 0, 6 3
с
с

15. Разбивочные размеры

2
0
l
p
24 R
2
l0
0
2C
C Rlo
m x0 R sin o
l0
m0 m p tg
2
2

16. Разбивочные размеры

Lкк R 2 0
Должно выполняться условие:
Lкк 30 м
Lкр 2l0 R 2 0

17. Разбивочные размеры

Т кр m R p tg
R p
Б
R
cos
2
2

18.

Разбивка переходной кривой осуществляется по координатам Хi и Yi
причем
в точке НПК -
xнпк 0
унпк 0
а точке КПК -
xкпк х0
укпк у0
Их определение зависит от вида переходной кривой, которая может соответствовать кубической параболе или радиоидальной спирали.

19.

Кубическую параболу применяют при условии:
R 1, 602C
5
9
В этом случае координаты Х и У определяются по формулам:
xi xi 1 x
0 xi x0 l0
xi3
yi
6C

20.

В противном случае разбивка переходной кривой производиться по радиоидальной спирали и координаты переходной кривой определяются по уравнениям:
l
xi li 1
2
40C
4
i
3
i
2
i
l
l
yi
6C
6R

21. Разбивочные размеры

Точке КПК соответствуют координаты:
l
x0 lo 1
2
40C
4
o
3
0
2
0
l
l
y0
6C
6R

22. Последовательность расчета переходной кривой

23.

1
Определяется длина переходной кривой
h
l0
i
и проверяется условие:
lo 0, 32Vmax

24.

2
Определяются величина угла поворота переходной кривой:
2
0
l
0
2C

25.

3
Проверяется возможность устройства переходной кривой
при известном угле поворота β (в радианах) и радиусе R
2 0
Lкк R 2 0 30 м
Если условие не выполняется, то изменяют величину R и
переходят к пункту №1.

26.

4
Определяется вид переходной кривой и координаты для
ее разбивки.
Для этой цели прежде всего проверяется возможность
применить в качестве переходной кривой кубическую параболу:
5
R 1, 602C 9
Если условие выполняется, то координаты определяются
по уравнениям:
xi xi 1 x
0 xi x0 l0
3
i
x
yi
6C

27.

5
В противном случае для разбивки переводной кривой
применяют радиоидальную спираль. Координаты определяются по уравнениям:
l
xi li 1
2
40C
4
i
3
i
2
i
l
l
yi
6C
6R

28.

6
Определяется величина сдвижки:
2
0
l
p
24 R
Расстояние от начала переходной кривой до отнесенной
точки тангенса:
m x0 R sin o
Расстояние от начала переходной кривой до первоначального тангенсного столбика:
l0
m0 m p tg
2
2

29.

7 L 2l R 2
Определяется полная длина кривой:
кр
0
суммарный тангенс новой кривой:
Т кр m R p tg
и суммарная биссектриса:
R p
Б
R
cos
2
0
2