Похожие презентации:
Теория электромагнитного поля. Законы и основные уравнения электромагнитного поля
1. МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ГРАЖДАНСКОЙ АВИАЦИИ ИРКУТСКИЙ ФИЛИАЛ КАФЕДРА АВИАЦИОННЫХ ЭЛЕКТРОСИСТЕМ И
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТГРАЖДАНСКОЙ АВИАЦИИ
ИРКУТСКИЙ ФИЛИАЛ
КАФЕДРА АВИАЦИОННЫХ ЭЛЕКТРОСИСТЕМ И ПИЛОТАЖНОНАВИГАЦИОННЫХ КОМПЛЕКСОВ
ЛЕКЦИЯ № 2.2
по дисциплине
Теория электромагнитного поля
ТЕМА № 2
Законы и основные уравнения электромагнитного
поля
2. Вопросы лекции
25Вопросы лекции
2.1. Электростатическое поле.
2.1.5. Проводники в электростатическом поле.
2.1.6. Энергия и силы в электростатическом поле.
2.1.7. Методы расчета электростатических полей
3. 2.1.5. Проводники в электростатическом поле.
24К проводникам относят вещества, в которых имеются заряженные частицы,
способные двигаться упорядоченно по всему объему тела под действием
электрического поля. Заряды таких частиц называются свободными.
Проводниками являются все металлы, некоторые химические соединения,
водные растворы солей, кислот, щелочей, расплавы солей, ионизированные
газы. В металлах носителями свободных зарядов являются свободные
электроны, называемые электронами проводимости.
4.
23Если внести незаряженный металлический проводник в однородное
электростатическое поле (рис.), то под действием поля в нем возникнет
упорядоченное движение свободных электронов металла в направлении,
противоположном направлению напряженности Ео этого поля. Электроны
будут скапливаться на одной стороне проводника, образуя там избыточный
отрицательный заряд, а их недостача на другой стороне проводника приведет
к образованию там избыточного положительного заряда, т.е. в проводнике
произойдет пространственное разделение зарядов.
Эти некомпенсированные разноименные заряды появляются на проводнике
только под действием внешнего электрического поля, т. е. такие заряды
являются индуцированными (наведенными), а в целом проводник попрежнему остается незаряженным.
5.
22Такой вид электризации, при котором под действием внешнего
электрического поля происходит перераспределение зарядов между
частями данного тела, называют электростатической
индукцией. Появившиеся вследствие электростатической индукции на
противоположных частях проводника нескомпенсированные электрические
заряды создают свое собственное электрическое поле, его напряженность
Ес внутри проводника направлена против напряженности Ео внешнего поля, в
которое помещен проводник.
По мере разделения зарядов в проводнике и накопления их на
противоположных частях проводника напряженность Ее внутреннего поля
увеличивается и, наконец, становится равной (по модулю) напряженности
Ео внешнего поля. Это приводит к тому, что напряженность Е результирующего
поля внутри проводника становится равной нулю. При этом наступает
равновесие зарядов на проводнике.
6.
При равновесии зарядов на проводнике весь некомпенсированный заряд 21находится только на наружной поверхности проводника, а внутри
проводника электрическое поле отсутствует.
Поверхность проводника будет границей электростатического поля, которое
локализовано в диэлектрике, окружающем проводник.
Это явление используют при создании электростатической защиты,
сущность которой состоит в том, что для предохранения чувствительных
приборов от влияния электрических полей их помещают в металлические
заземленные корпуса или сетки.
Таким образом,
1) весь избыточный заряд проводника оказывается на его поверхности,
внутри проводника зарядов нет;
2) внутри проводника напряженность электростатического поля равна нулю;
3) поверхность проводника является эквипотенциальной;
4) потенциал всех точек внутри проводника равен потенциалу на его
поверхности.
7.
Граничные условия в электростатическом поле20
При переходе электрического поля через границу раздела двух
диэлектрических сред обе векторные характеристики поля – вектор
напряженности E и вектор смещения D скачкообразно изменяются по величине
и направлению.
Граничные условия – соотношения, характеризующие эти изменения. Таких
условий четыре.
Нормальные составляющие E и D
Рассмотрим границу двух непроводящих сред, диэлектрические
проницаемости которых равны 1 и 2 (рис. 2).
Поверхность разделяющая эти диэлектрики
обозначена буквой S.
Выделим замкнутую поверхность
цилиндрической формы с основаниями,
параллельными поверхности S и длиной
образующей, равной l. Эту замкнутую
цилиндрическую поверхность обозначим буквой
(сигма).
Рис. 2
8.
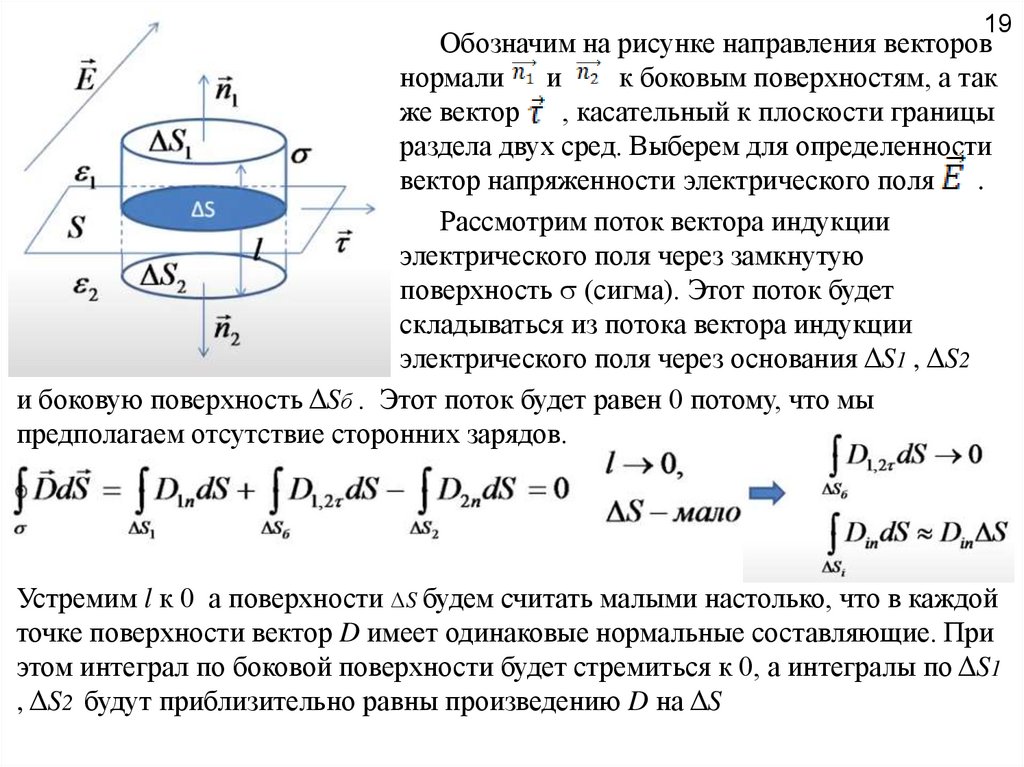
19Обозначим на рисунке направления векторов
нормали и
к боковым поверхностям, а так
же вектор , касательный к плоскости границы
раздела двух сред. Выберем для определенности
вектор напряженности электрического поля
.
Рассмотрим поток вектора индукции
электрического поля через замкнутую
поверхность (сигма). Этот поток будет
складываться из потока вектора индукции
электрического поля через основания ΔS1 , ΔS2
и боковую поверхность ΔSб . Этот поток будет равен 0 потому, что мы
предполагаем отсутствие сторонних зарядов.
Устремим l к 0 а поверхности ΔS будем считать малыми настолько, что в каждой
точке поверхности вектор D имеет одинаковые нормальные составляющие. При
этом интеграл по боковой поверхности будет стремиться к 0, а интегралы по ΔS1
, ΔS2 будут приблизительно равны произведению D на ΔS
9.
18Отсюда получаем
Это позволяет преобразовать выражение для
потока D через замкнутую поверхность к виду
..
Сокращаем на ΔS и получаем
, т.е. нормальные
Составляющие вектора D на границе двух
сред не претерпевают разрыва.
Используя соотношение между индукцией и
напряженностью электрического поля,
запишем
.
.
Следовательно нормальная составляющая напряженности электрического
поля испытывает скачек на границе двух диэлектриков.
Далее рассмотрим тангенциальные составляющие векторов Е и D
10.
Тангенциальные составляющие векторов Е и D17
Пусть горизонтальная черта представляет собой границу раздела двух
диэлектриков с диэлектрическими проницаемостями 1 и 2 , которые мы
наблюдаем с ребра. Рассмотрим замкнутый контур L , образованный отрезками
L1 и L3, параллельными границе раздела и L2 и L4, перпендикулярными границе
раздела. Пусть длины отрезков L1 и L3 равны Δа и L2 и L4 равны Δb. Выберем
для определенности направление вектора напряженности электрического поля и
направления векторов и . Нормального вектора к границе раздела двух сред
и тангенциального.
Найдем циркуляцию напряженности
электрического поля по замкнутому контуру L.
Этот интеграл может быть записан:
Циркуляция вектора напряженности
электрического поля равна 0 поскольку
электростатическое поле потенциально.
11.
16Устремим Δb к 0, а Δа будем выбирать
столь малым, чтобы в каждой точке отрезка L1
и L3 значения тангенциальных составляющих
напряженности были одинаковы. Тогда
запишем:
Откуда, сокращая на Δа, получим
Из этого делаем вывод, что тангенциальная составляющая напряженности
электрического поля непрерывна при переходе на разделе двух диэлектрических
сред.
Используя связь напряженности и индукции электрического поля запишем
равенство тангенциальных составляющих напряженности в виде:
12.
Преломление линий D и E на границе двух диэлектриков15
Пусть над границей раздела расположен
дтэлектрик с диэлектрической проницаемостью 1 , а
под границей с диэлектрической проницаемостью 2>
1.
Рассмотрим электрическое поле, которое в первой
среде определяется вектором Е1. Разложим этот
вектор на составляющие: перпендикулярную границе
раздела E1n и параллельную E1τ. Как мы выяснили:
тангенциальная составляющая не испытывает
разрыва, а нормальная составляющая скачкообразно
меняется. Если 2> 1 , то E1n>E2n. Соответственно
результирующая векторов E1τ и E2n имеет другой угол
преломления. Мы видим, что углы, образуемые
векторами напряженности в первой и второй среде
различаются.
13.
Теперь рассмотрим поведение силовых 14линий вектора D.
Индукция вектора напряженности в
первой среде определяется вектором D1.
Аналогично разложим вектор на
составляющие и воспользуемся граничными
условиями.
Видим, что если 2> 1 , то D2τ > D1τ
D1n=D2n. Результирующий вектор имеет
другой угол преломления.
Мы видим, что углы, образуемые
векторами индукции с нормалью в первой и
второй среде различаются, т.е. имеет место
преломление на разделе двух сред силовых
линий.
Обе векторные характеристики электрического поля: напряженность и
индукция испытывают скачек, меняются по величине и по направлению при
переходе границы двух сред.
Испытывает ли при этом скачек потенциал?
14.
Непрерывность потенциала.13
Предположим, что потенциал φ испытывает скачек на границе раздела двух
диэлектриков. Пусть диэлектрические проницаемости этих диэлектриков 1 и
2.
Направим перпендикулярно границе раздела двух сред ось Х. И будем
считать, что слева от границы потенциал будет иметь одно значение, а справа
другое. Т.к. напряженность электрического поля равна минус градиент от
потенциала, то компонента напряженности по х будет равна минус dφ по dx.
Эта производная будет стремиться к бесконечности в том случае, если dx будет
стремиться к 0, а dφ будет иметь конечную величину, т.е. потенциал будет
иметь скачек.
Бесконечное значение для напряженности электрического поля показывает,
что результат является бессмысленным и, следовательно предположение о том,
что потенциал испытывает скачек на границе двух диэлектриков является
неверным.
15. 2.1.6. Энергия и силы в электростатическом поле.
12Энергия электростатического поля - это энергия системы неподвижных
точечных зарядов, энергия уединенного заряженного проводника и энергия
заряженного конденсатора.
Как заметили, заряженные тела, в частности, заряженный
конденсатор, обладают энергией. Однако где же заключена энергия – в
заряженных телах или в электрическом поле, обеспечивающем взаимодействие
зарядов. Опыт подсказывает, что эта энергия заключена в электрическом поле.
Для нахождения энергии электрического поля рассмотрим заряженный
плоский конденсатор. Преобразуем энергию заряженного конденсатора,
используя выражения
и
E
d
U
- плотность энергии
16.
11Энергия взаимодействия дискретных зарядов.
- потенциальная энергия взаимодействия двух точечных зарядов.
- энергия взаимодействия системы дискретных зарядов
Энергия взаимодействия при непрерывном распределении заряда.
- - энергия взаимодействия системы непрерывных зарядов
Где φ— потенциал, создаваемый всеми зарядами в точке нахождения
заряда dq.
Собственная энергия.
Плотность энергии электрического поля и энергия электрического поля.
Энергия поля поверхностных зарядов.
Энергия заряженных проводников.
Энергия диполя во внешнем поле.
17.
Силы в электростатическом поле10
Сила Лоренца
На точечный заряд, помещенный в электрическое поле с напряженностью E
действует сила (Лоренца) равная F = qE.
На систему N штук точечных зарядов действует суммарная сила равная:
Плотность силы.
Для непрерывно распределенного заряда с плотностью ρ выражение для
силы, действующей на данную систему зарядов во внешнем поле имеет вид:
где f -сила действующая на единицу объема или плотность силы f = ρE.
Сила действующая на диполь.
18.
Энергия диполя зависит как от координат, так и от ориентации диполя по 9отношению к направлению поля. В связи с этим, на диполь действует не только
сила, приводящая к перемещению диполя в пространстве как целого, но еще и
момент силы стремящийся развернуть диполь, ориентируя его по направлению
поля. Величина момента N равна
Сила действующая на единицу объема диэлектрика.
Направление силы, действующей на диэлектрик не зависит от направления
поля. Сила, действующая на элементарный объем диэлектрика, направлена в
сторону максимального возрастания напряженности электростатического поля.
В однородном поле сила действующая на диэлектрик равна нулю.
Если вектор поляризации диэлектрика зависит нелинейным образом от
плотности диэлектрика ρm говорят о силе с учетом сжимаемости диэлектрика.
Плотность силы в этом случае определяется выражением:
19.
8Сила действующая на проводник
При рассмотрении сил действующих на вещество специального
рассмотрения требуют проводники в связи с тем, что поле внутри проводников
равно нулю, а весь заряд распределен по поверхности проводника. Очевидно,
заряды на поверхности конечного проводника отталкиваются друг от друга
пытаясь разорвать проводник, то есть на поверхности возникает сила, связанная
с кулоновским отталкиванием зарядов одноименного знака.
На единице поверхности проводника возникает давление, равное:
При наличии границы проводник диэлектрик давление равно:
20.
72.1.7. Методы расчета электростатических полей
Основной прикладной задачей электростатики является расчет
электростатических полей, создаваемых в различных приборах и аппаратах
(конденсаторы, кабели, электровакуумные приборы и т.д.) В общем виде эта
задача решается с помощью закона Кулона и принципа суперпозиции.
Однако, этот путь очень сложен. При наличии большого количества точечных
зарядов эта задача сводится к сложному суммированию или интегрированию.
Поэтому для практического решения основных задач электростатики был
разработан целый ряд вспомогательных методов и приемов.
Один из наиболее распространенных методов - использование теоремы
Остроградского-Гаусса. Эта теорема связывает поток вектора напряженности
через произвольно замкнутую поверхность с электрическим зарядом,
находящимся внутри этой поверхности.
Использование теоремы Гаусса для расчета полей эффективно в тех случаях,
когда поле обладает специальной симметрией (чаще всего плоской,
цилиндрической или сферической). Симметрия и конфигурация поля должны
быть такими, чтобы, во-первых, заряженное тело можно было бы окружить
достаточно простой замкнутой поверхностью и, во-вторых, вычисление потока
вектора напряженности свести к простому умножению Е (или En) на площадь
поверхности S или часть ее. Если этого сделать нельзя, то задачу необходимо
решать другими методами.
21.
6Расчет электростатических полей чаще всего сводится к определению
напряженности поля Е при заданном распределении зарядов, возбуждающих
поле. Если непосредственное определение Е приводит к математическим
трудностям, удобнее вначале определить потенциал по заданному
распределению зарядов, а затем, зная потенциал, определить напряженность
поля. Обратная задача заключается в определении закона распределения
зарядов по заданной напряженности поля.
Наиболее общим методом расчета полей является метод интегрирования
уравнений поля. Однако в ряде случаев можно использовать частные методы,
которые позволяют проще и быстрее решить поставленную задачу. К ним
относятся: метод наложения; метод, основанный на применении теоремы
Гаусса; метод конформных преобразований; метод зеркальных изображений;
графические и ряд других методов. Рассмотрим некоторые из перечисленных
методов.
22.
5Метод наложения
Если распределение заряда в пространстве задано, то, разделив этот заряд на
бесконечно малые элементы dQ и считая их точечными, можно определить
потенциал и напряженность поля по формулам
.
Складывая алгебраически величины
любой точке поля
, можно определить потенциал в
Напряженность определится по формуле
23.
4Метод зеркальных изображений
Если электрические заряды расположены вблизи границы двух разнородных
сред, то векторы поля можно определить, применив искусственный метод
расчета, который носит название метода зеркальных изображении.
Идея метода заключается в том, что вместо неоднородной среды
рассматривается однородная среда, влияние же неоднородности учитывается
введением фиктивных зарядов. Определив векторы поля от совместного
действия заданных и фиктивных зарядов, записывают граничные условия
основной задачи и, пользуясь ими, находят искомые векторы поля.
24.
Распределение потенциалов и зарядов в системе проводящих телПри исследовании процессов в линиях электропередач может встретиться
следующая задача. Дано несколько параллельных проводов. Взаимное их
расположение и электрические заряды на них известны. Требуется определить
потенциалы этих проводов. Обозначим потенциал произвольной точки р,
обусловленный зарядом одного из проводов
через
. Так как потенциал и
заряд пропорциональны, то
Коэффициент
—величина постоянная. Если число всех проводов
обозначить п, то потенциал в точке р, обусловленный зарядами всех проводов,
можно определить, пользуясь принципом наложения
Если точку р выбрать на поверхности первого провода, то его потенциал
………
3
25.
2Предположим, что все заряды, кроме , равны нулю, a
. Тогда
.
Следовательно, коэффициент численно равен потенциалу провода k, когда заряд
провода
равен единице, а заряды остальных проводов равны нулю.
Постоянные В называются потенциальными коэффициентами. Они всегда
положительные. При перестановке индексов коэффициент не
изменяется:
. Если полученную систему уравнений решить относительно
зарядов, то
Постоянные А называются емкостными коэффициентами. Связь между
потенциальными и емкостными коэффициентами следующая
где определитель системы
26.
а алгебраическое дополнение:1
Коэффициенты А с одинаковыми индексами положительны, с различными
индексами — отрицательны. При перестановке индексов коэффициент не
меняется
. Пусть потенциал одного из проводов, например
, равен
единице, а потенциал остальных проводов равен нулю. Тогда
.
Следовательно, коэффициент
численно равен заряду
, когда
потенциал
, а потенциал остальных проводов равен нулю.
Систему уравнений можно записать иначе
где
Коэффициенты С называются частичными емкостями. Если индексы у
частичной емкости одинаковые, ее называют собственной частичной емкостью,
если индексы разные - взаимной частичной емкостью. Частичные емкости
всегда положительные. При изменении порядка индексов коэффициент не
меняется
. Коэффициенты А могут быть определены экспериментально.
Зная их, можно подсчитать частичные емкости.
27.
Задача на теорему Гаусса №1: напряженность поля плоскостиУсловие
Определите напряженность поля бесконечной заряженной плоскости.
Поверхностная плотность заряда сигма.
Решение
Линии напряженности перпендикулярны рассматриваемой плоскости и
направлены в обе стороны от неё. Выберем в качестве гауссовой поверхности
цилиндр с основанием, параллельным плоскости:
По теореме Гаусса:
Поток сквозь цилиндр равен сумме потоков сквозь
боковую поверхность цилиндра и потокам сквозь оба
его основания. Поток сквозь боковую поверхность
равен нулю, так как линии напряженности параллельны ей:
Согласно теореме Гаусса:
Отсюда:
28. заключение
Т. о., в результате рассмотрения материала вы получили знания :- об основных понятиях и определениях электротехники;
- идеализированных элементах электрических цепей;
- основных законах электротехники;
- методах преобразования электрических цепей.



























 Физика
Физика








