Статистические методы оценки, анализа и контроля надежности

1.

СТАТИСТИЧЕСКИЕ МЕТОДЫ ОЦЕНКИ, АНАЛИЗА И КОНТРОЛЯ
НАДЕЖНОСТИ
Вероятностные показатели надежности невосстанавливаемых элементов
Надежность систем электроснабжения зависит от множества факторов, большинство из которых являются
случайными. Для практических расчетов в системах электроснабжения применяют количественные
характеристики надежности, полученные методами теории вероятности и математической статистики:
1) Вероятность безотказной работы P(t) – это вероятность того, что в заданном интервале t при
определенных режимах и условиях эксплуатации не произойдет ни одного отказа:
P(t) = P{T ≥ t},
(3.1)
где T - время непрерывной работы системы до первого отказа.
Эта функция наиболее полно определяет надежность системы и ее отдельных элементов. На практике ее
можно определить, зная статистические (эксплуатационные) данные об отказах, по выражению:
(3.2)
где Nо - начальное число исследуемых элементов;
n(t) - число элементов, отказавших за время t .
2) Вероятность отказа Q(t) – это вероятность того, что в заданном интервале времени t произойдет хотя бы
один отказ:
Q(t) = P{T ≤ t}.
(3.3)
Поскольку вероятность отказа и вероятность безотказной работы – события несовместные и
противоположные, справедливо равенство:
Q(t) =1− P(t) .
(3.4)
Для статистического определения вероятности отказа можно
пользоваться формулой:
(3.5)

2.

3.

3.2. Статистические показатели надежности
восстанавливаемых систем
Особенностью восстанавливаемых объектов является циклический характер работы, когда за
работоспособным состоянием следует отказ, затем восстановление и повторный ввод в эксплуатацию.
Таким образом весь период жизни элемента является непрерывным потоком отказов и восстановлений
(рис. 3.1).

4.

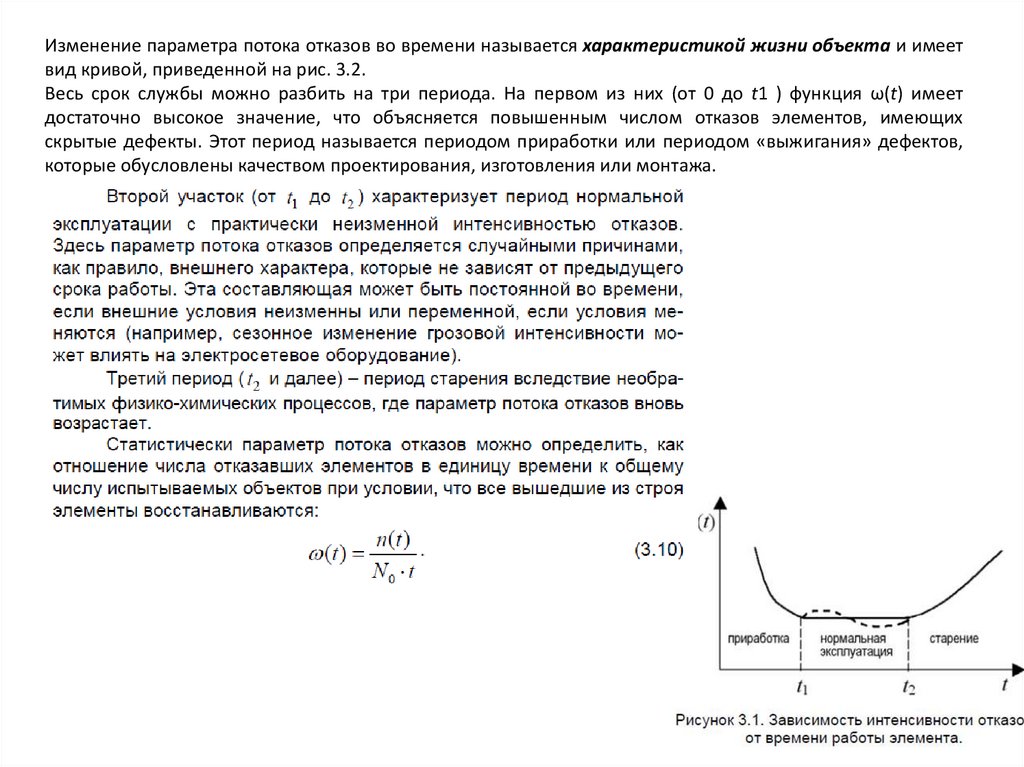
Изменение параметра потока отказов во времени называется характеристикой жизни объекта и имеет
вид кривой, приведенной на рис. 3.2.
Весь срок службы можно разбить на три периода. На первом из них (от 0 до t1 ) функция ω(t) имеет
достаточно высокое значение, что объясняется повышенным числом отказов элементов, имеющих
скрытые дефекты. Этот период называется периодом приработки или периодом «выжигания» дефектов,
которые обусловлены качеством проектирования, изготовления или монтажа.

5.

6.

где N – число испытываемых
образцов;
rj – число отказов j -го образца;
τ j i – время восстановления j -го
образца после i -го отказа.

7.

8.

9.

10.

Случайные величины
Основным в теории вероятностей является понятие случайной величины, т.е. величины,
которая в результате опыта может принимать то или иное неизвестное ранее значение.
Случайные величины могут быть дискретными и непрерывными. Примером дискретной
случайной величины может служить количество отказов системы электроснабжения за
какой-либо период (1, 2,3 и т.д.).
Случайные величины, возможные значения которых непрерывно заполняют некоторый
промежуток, называются непрерывными. Пример – время восстановления какого-либо
элемента системы, длительность простоя цеха из-за перерыва электроснабжения и т.п.
Соотношение, устанавливающее связь между возможными значениями случайной
величины и соответствующими им вероятностями, называется законом распределения
случайной величины.

11.

12.

Кроме того, для характеристики случайных величин широко используется плотность вероятности f (x)
= F′(x) , графически представляемая гистограммой или кривой распределения (рисунок 3.4. б).

13.

3.4. Законы распределения
случайных величин в теории
надежности
При исследовании надежности систем
электроснабжения
как
правило
используются теоретические законы
нормального и экспоненциального
распределения, закон Пуассона и
распределение Вейбулла.