Похожие презентации:
Площадь. Решение задач. Основные свойства площади многоугольника
1.
Решение задач по теме: «Площадь»2. Проверка домашнего задания
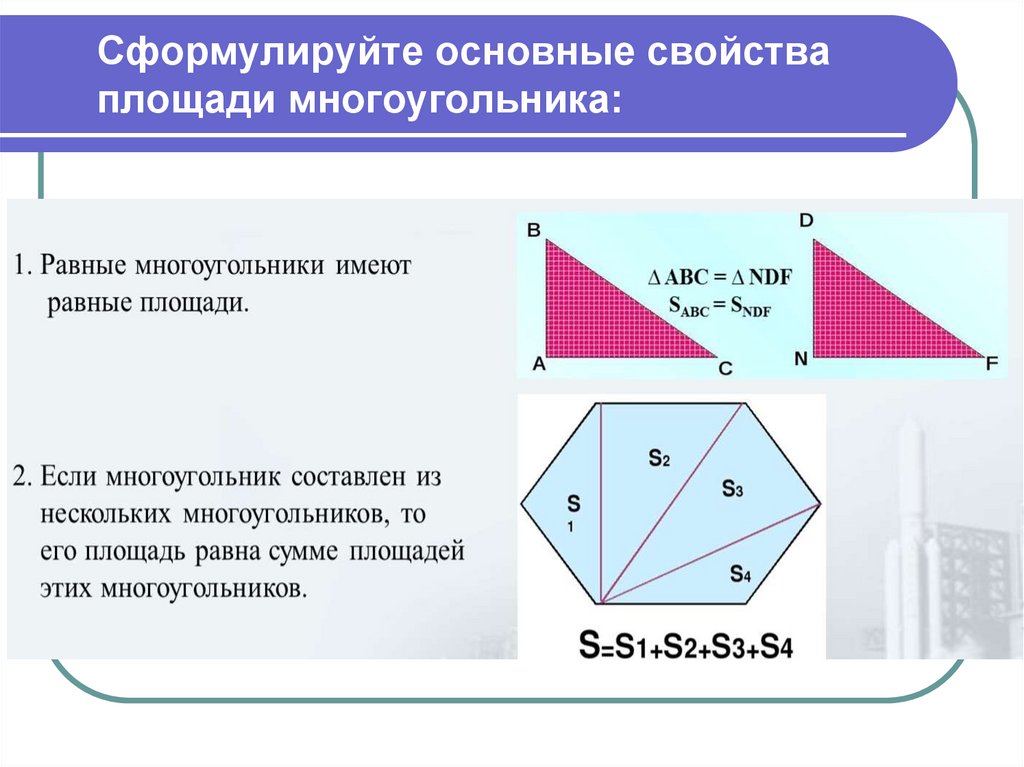
3. Сформулируйте основные свойства площади многоугольника:
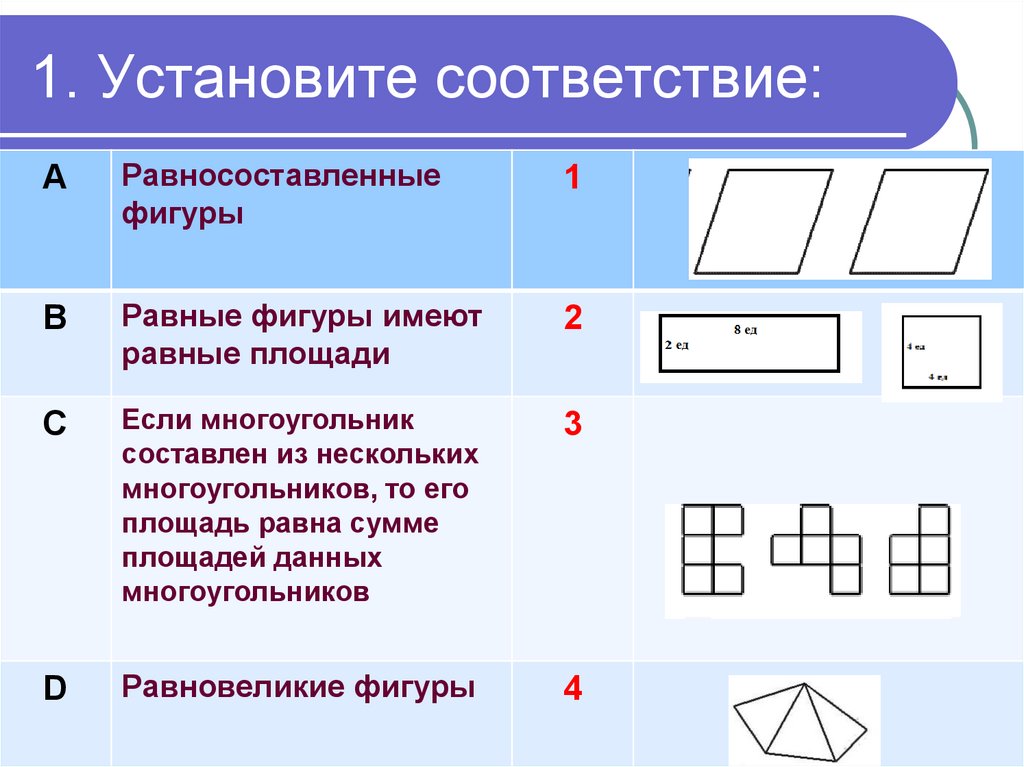
4. 1. Установите соответствие:
АРавносоставленные
фигуры
1
В
Равные фигуры имеют
равные площади
2
С
Если многоугольник
составлен из нескольких
многоугольников, то его
площадь равна сумме
площадей данных
многоугольников
3
D
Равновеликие фигуры
4
5. 2. Установите соответствие:
6. Устная работа
1) Сформулировать теоремуПифагора.
2) Сформулировать теорему
обратную теореме Пифагора.
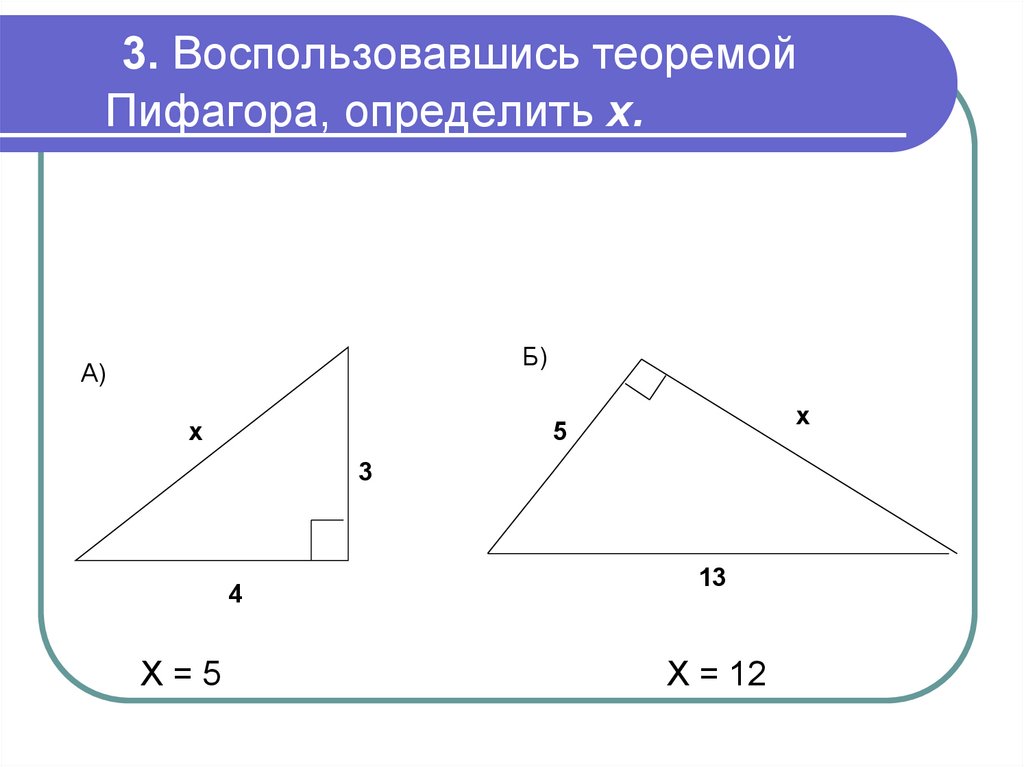
7. 3. Воспользовавшись теоремой Пифагора, определить х.
Б)А)
х
х
5
3
4
Х=5
13
Х = 12
8.
В тетрадях № 487 (из учебника)9. Изучение новой темы
Египетский треугольник.Треугольник со сторонами
3, 4, 5 назвали
египетским. Название
такое получил потому, что
еще в Древнем Египте
для построения прямых
углов на местности
использовали именно этот
способ.
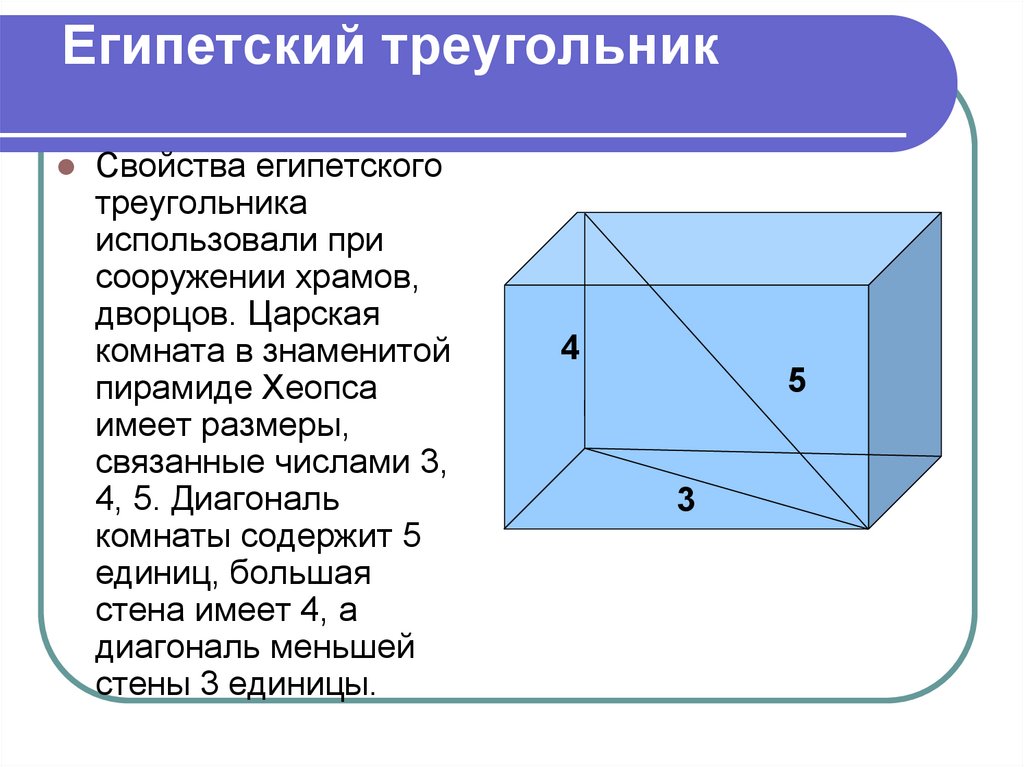
10. Египетский треугольник
Свойства египетскоготреугольника
использовали при
сооружении храмов,
дворцов. Царская
комната в знаменитой
пирамиде Хеопса
имеет размеры,
связанные числами 3,
4, 5. Диагональ
комнаты содержит 5
единиц, большая
стена имеет 4, а
диагональ меньшей
стены 3 единицы.
4
5
3
11. Пифагоровы треугольники
.Прямоугольные треугольники со сторонами, выраженными
целыми числами, называют пифагоровыми. Например,
треугольник со сторонами 5. 12, 13;
8, 15, 17 и т. д. И существует способ отыскания
«целочисленных» прямоугольных треугольников, т. е. таких
троек чисел, что с ² = а ² + в ².
Их можно найти по формулам:
в = (а ² – 1) / 2, с = (а ² + 1) / 2.
12. Решение задач.
1. Диагонали ромба равны14 и 48 см.Найдите площадь ромба, его сторону
и периметр.
13. Задание на дом
1. п. 55, 562. № 488(а), 490(а)









 Математика
Математика








