Похожие презентации:
Площади многоугольников. Свойства площадей
1.
Площадимногоугольников
2.
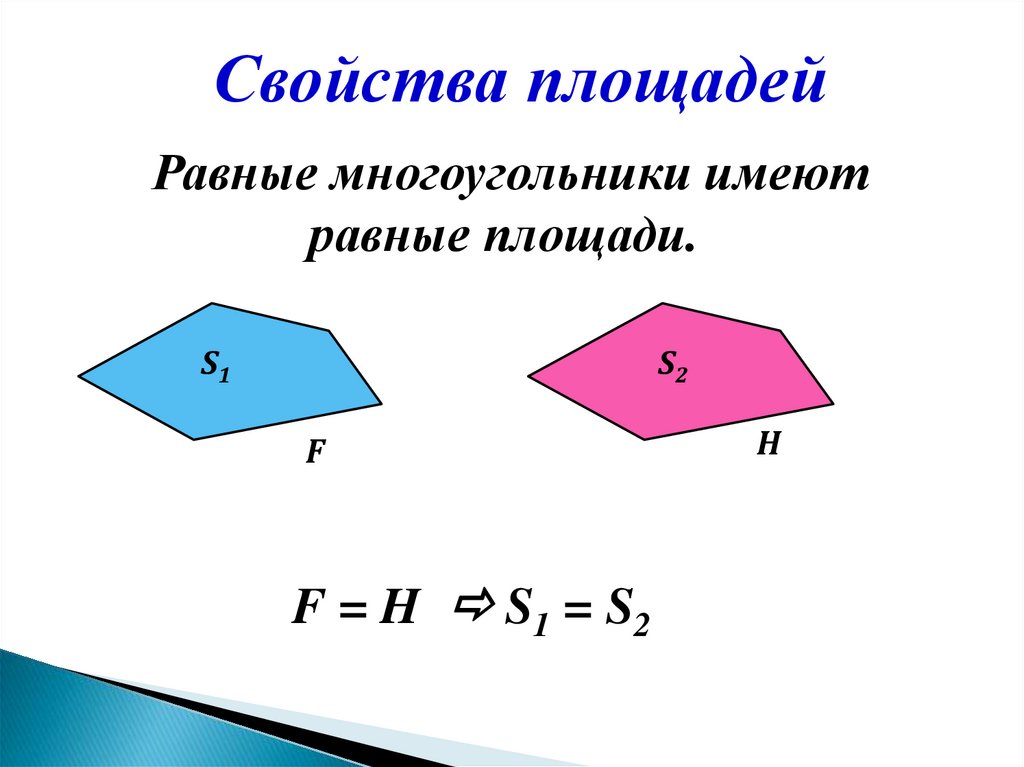
Свойства площадейРавные многоугольники имеют
равные площади.
S1
S2
F
F = H S1 = S2
H
3.
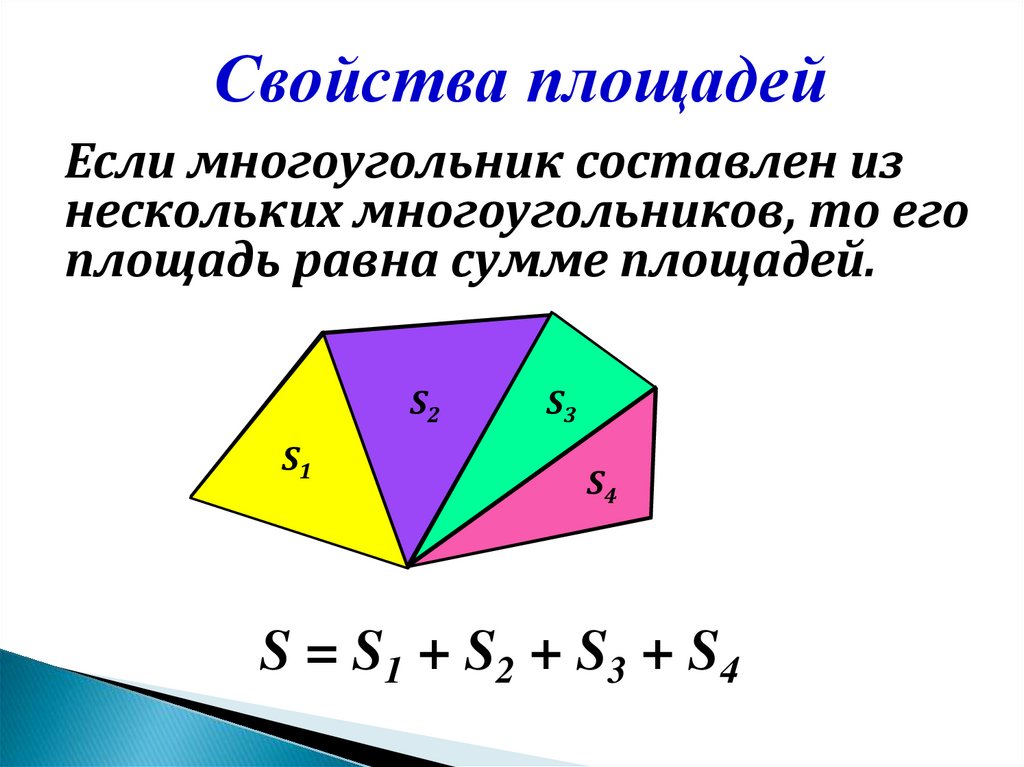
Свойства площадейЕсли многоугольник составлен из
нескольких многоугольников, то его
площадь равна сумме площадей.
S2
S1
S3
S4
S = S1 + S2 + S3 + S4
4.
Свойства площадейПлощадь квадрата равна
квадрату его стороны.
a
a
S a
2
5.
Площадь прямоугольникаa – длина
b
b- ширина
a
S ab
6.
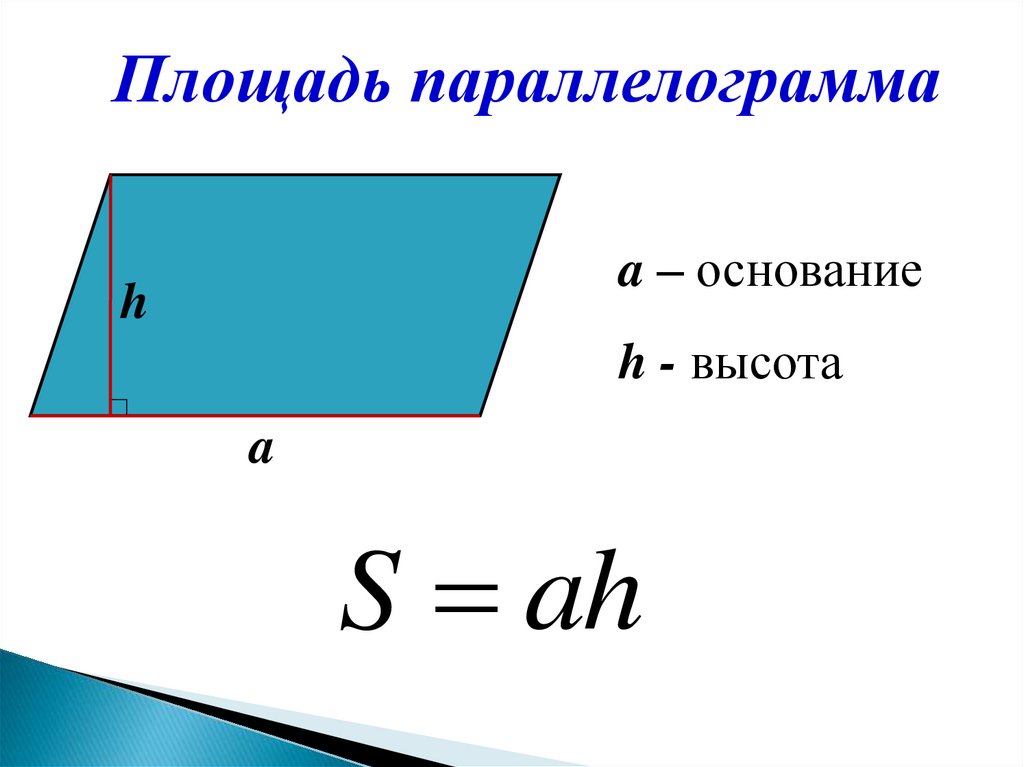
Площадь параллелограммаa – основание
h
h - высота
a
S ah
7.
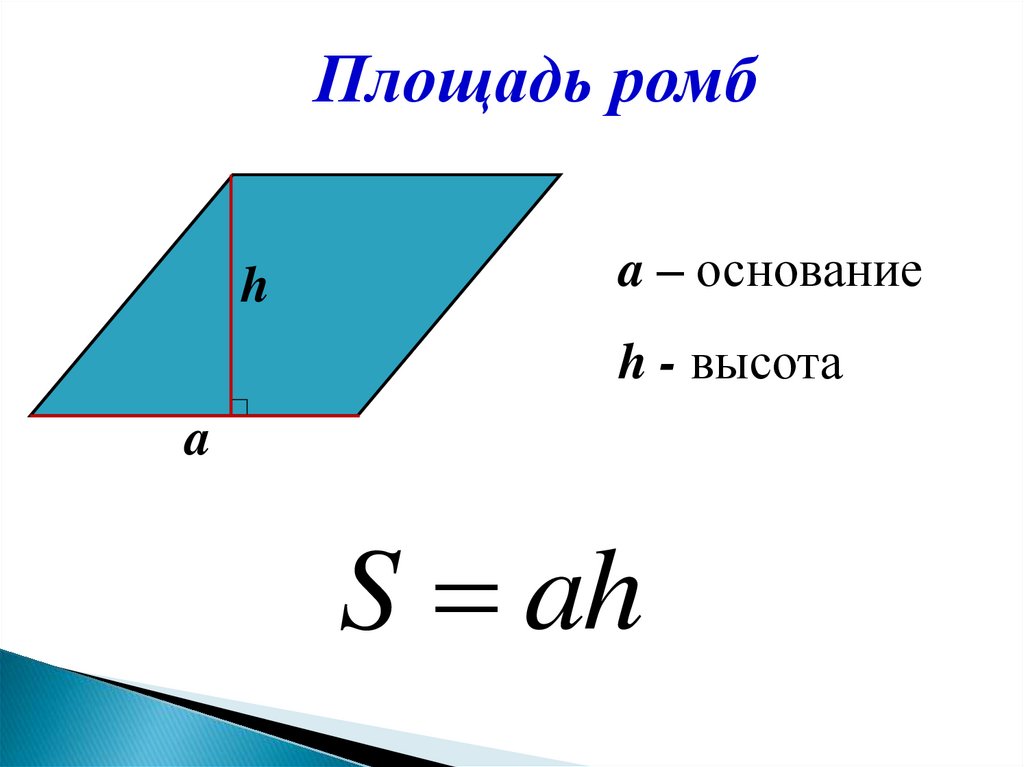
Площадь ромбh
a – основание
h - высота
a
S ah
8.
Задача 1Задача 2
5
7
S=49
12
S=60
9.
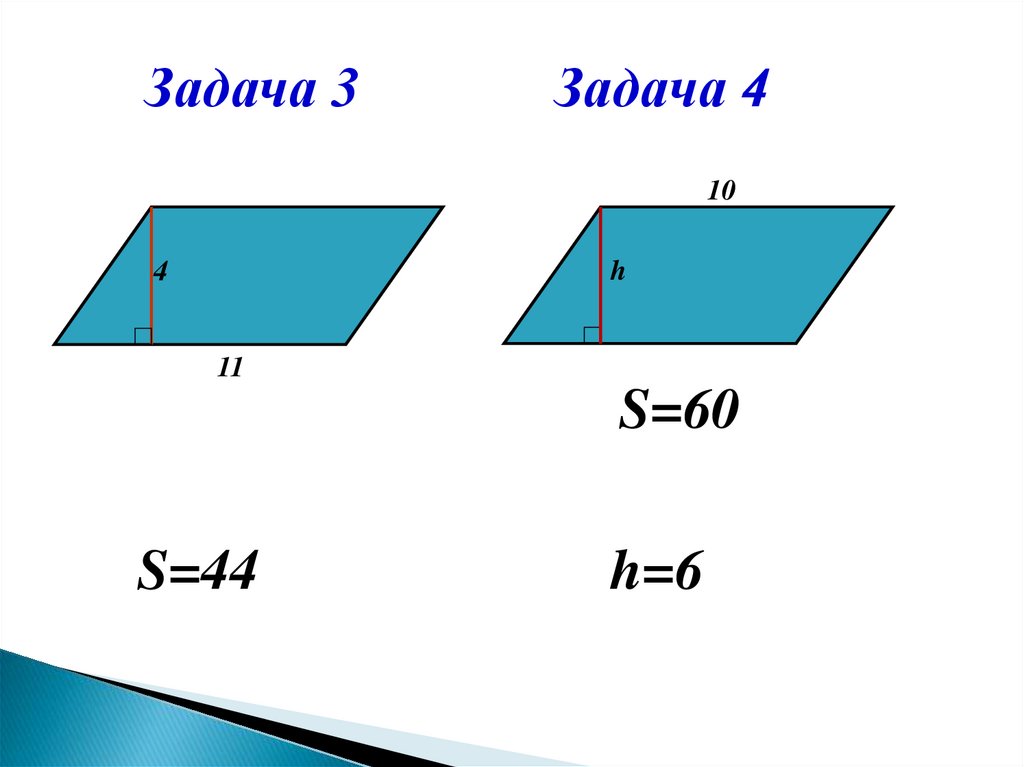
Задача 3Задача 4
10
h
4
11
S=60
S=44
h=6
10.
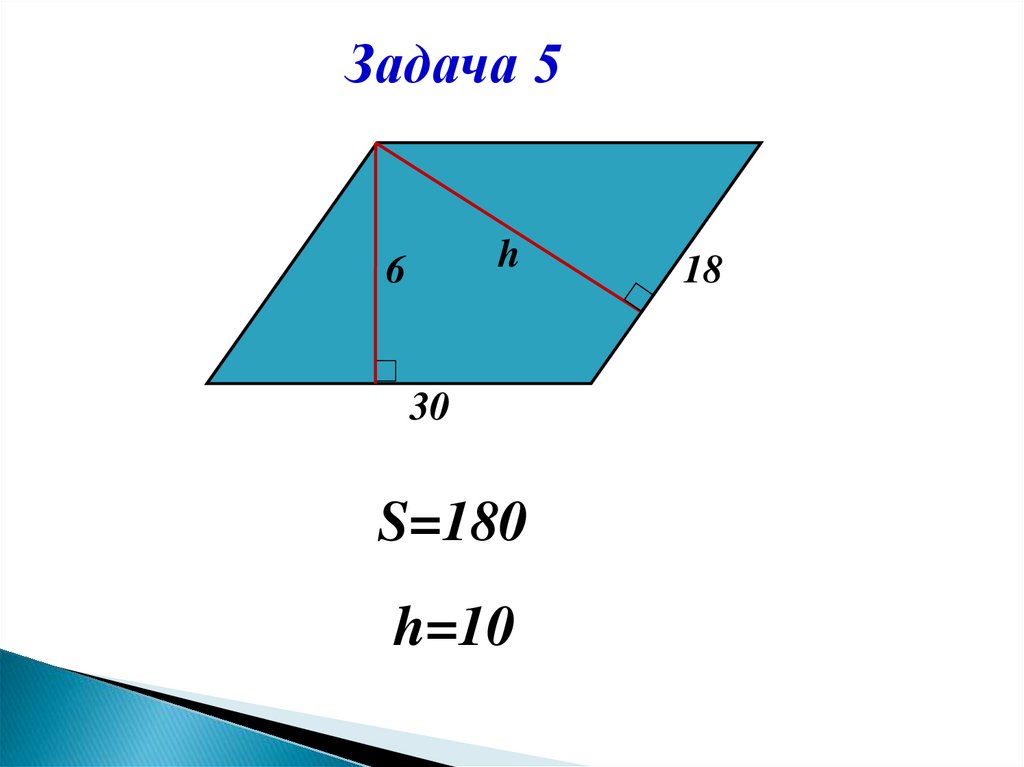
Задача 5h
6
30
S=180
h=10
18
11.
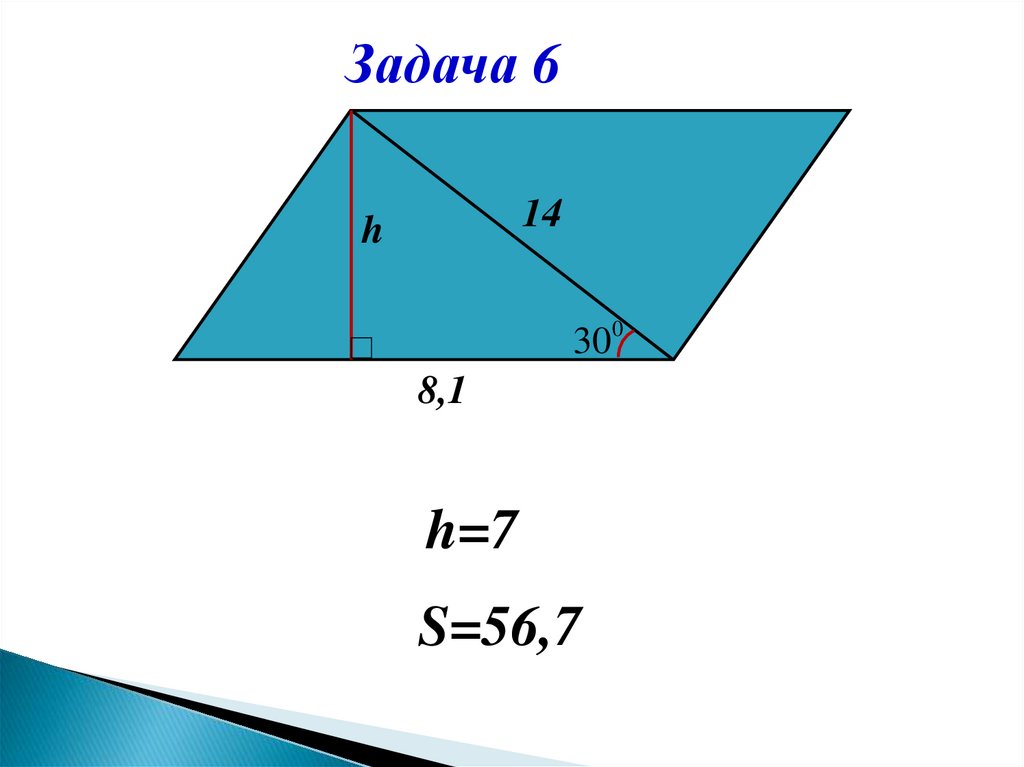
Задача 614
h
300
8,1
h=7
S=56,7
12.
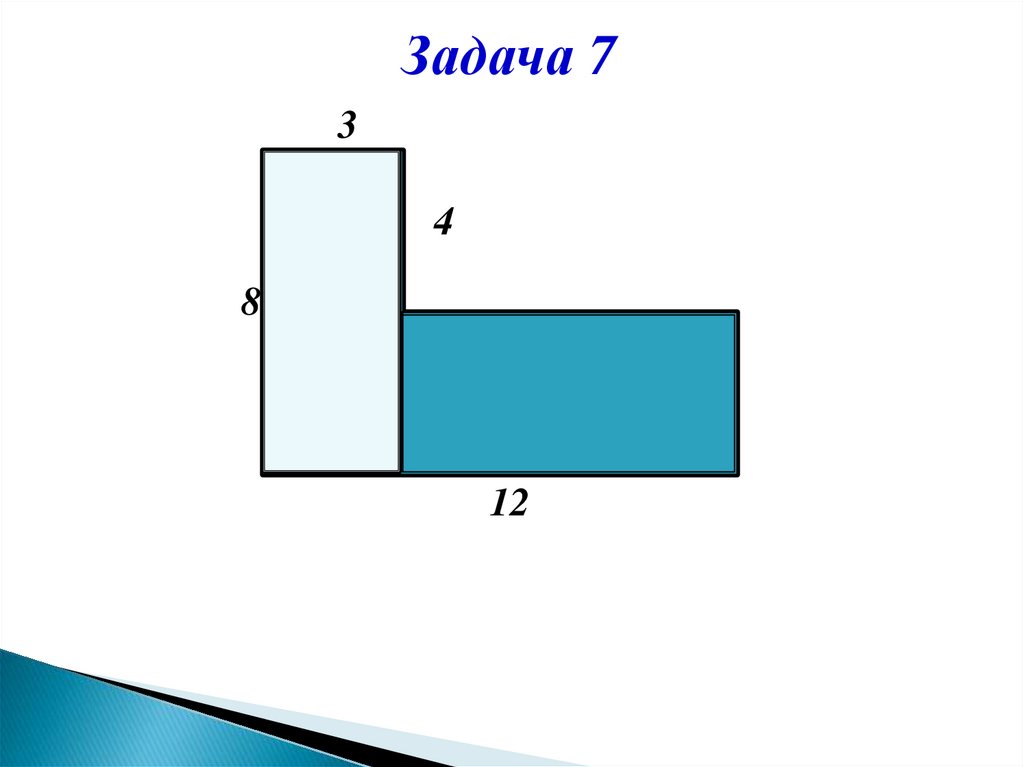
Задача 73
4
8
12
13.
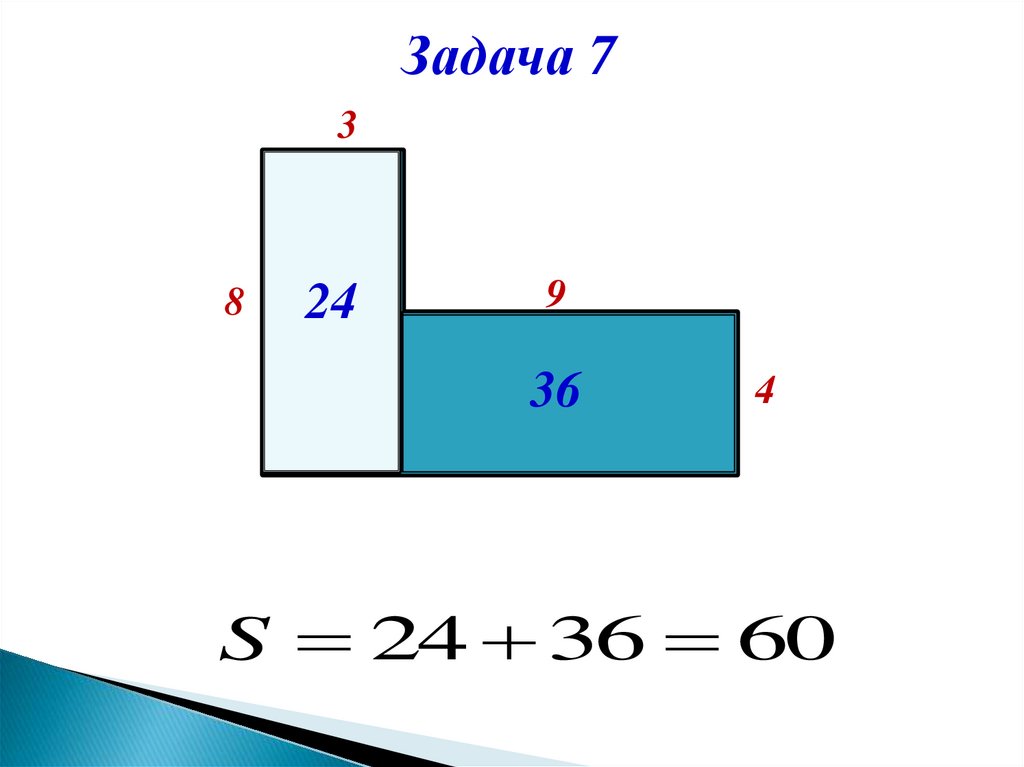
Задача 73
8
24
9
36
4
S 24 36 60
14.
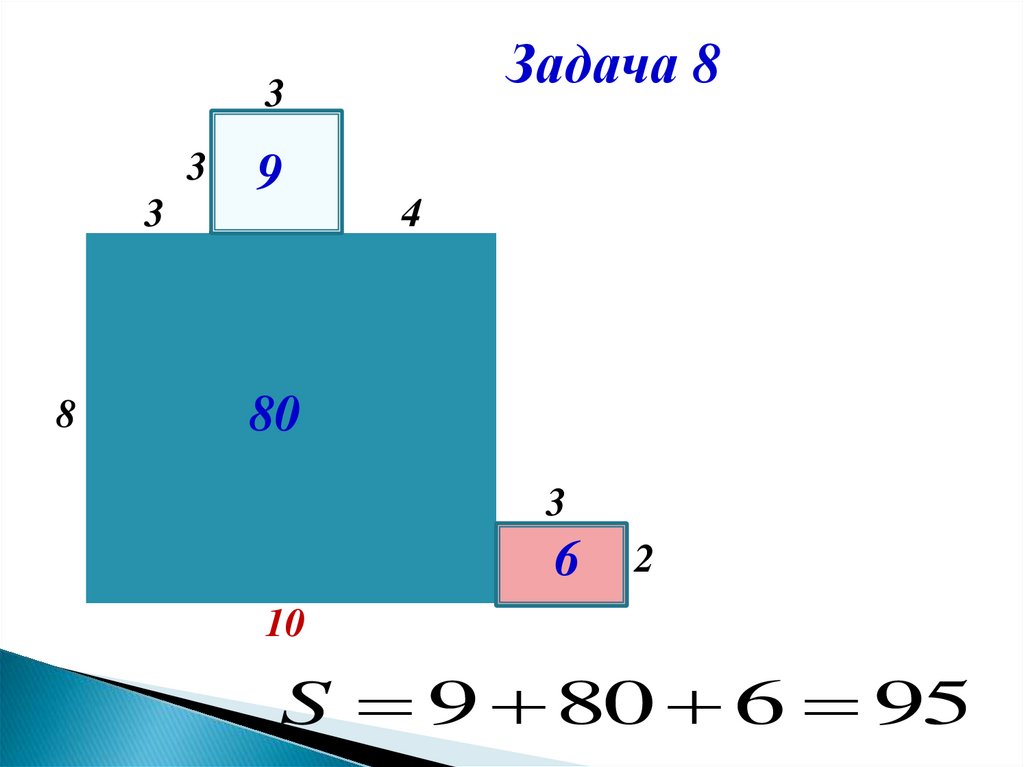
Задача 83
3
3
8
9
4
80
3
6
2
10
S 9 80 6 95
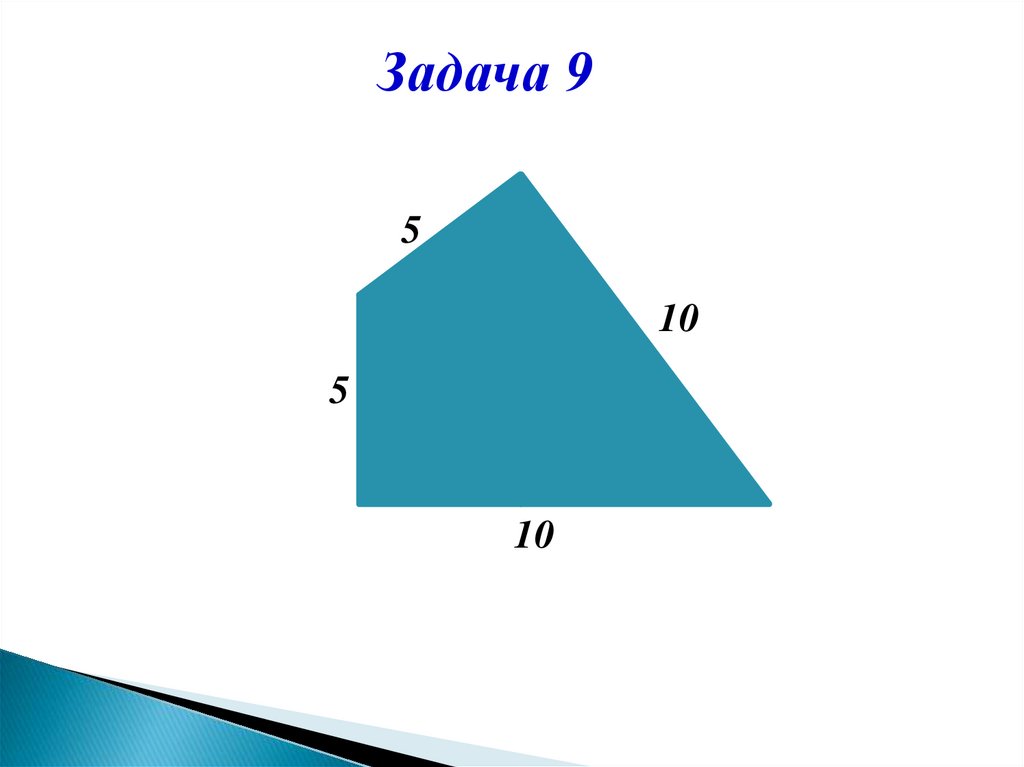
15.
Задача 95
10
5
10
16.
Человек, вооруженныйзнаниями способен
решить любые задачи.
17.
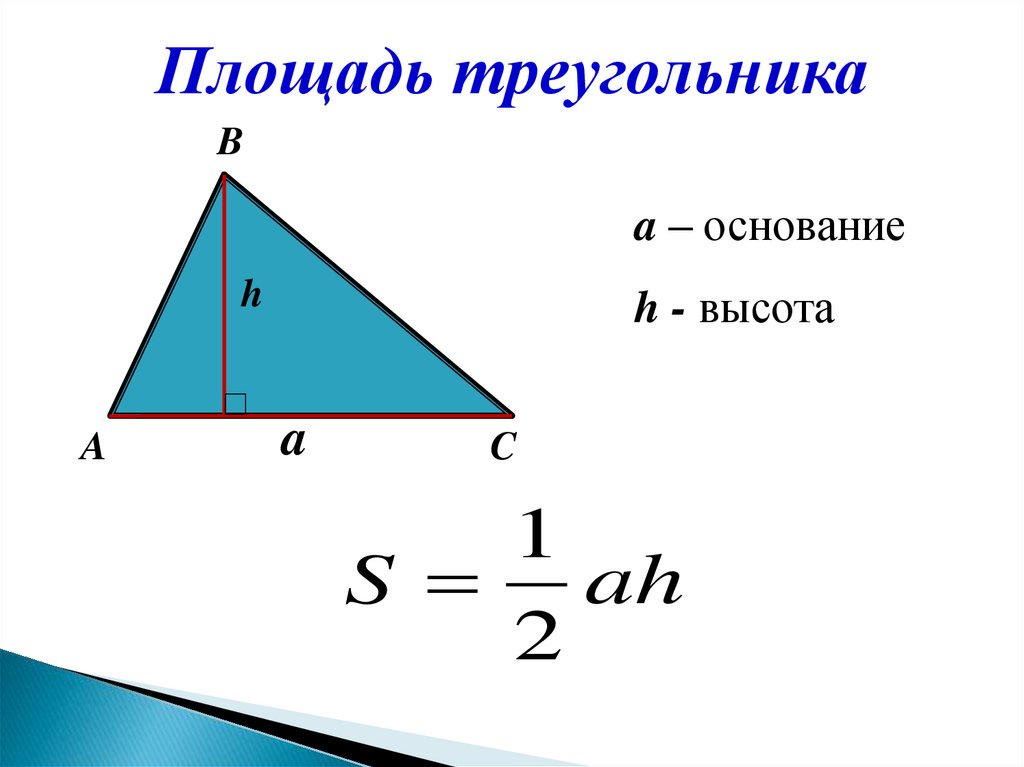
Площадь треугольникаB
a – основание
h
A
h - высота
a
C
1
S ah
2
18.
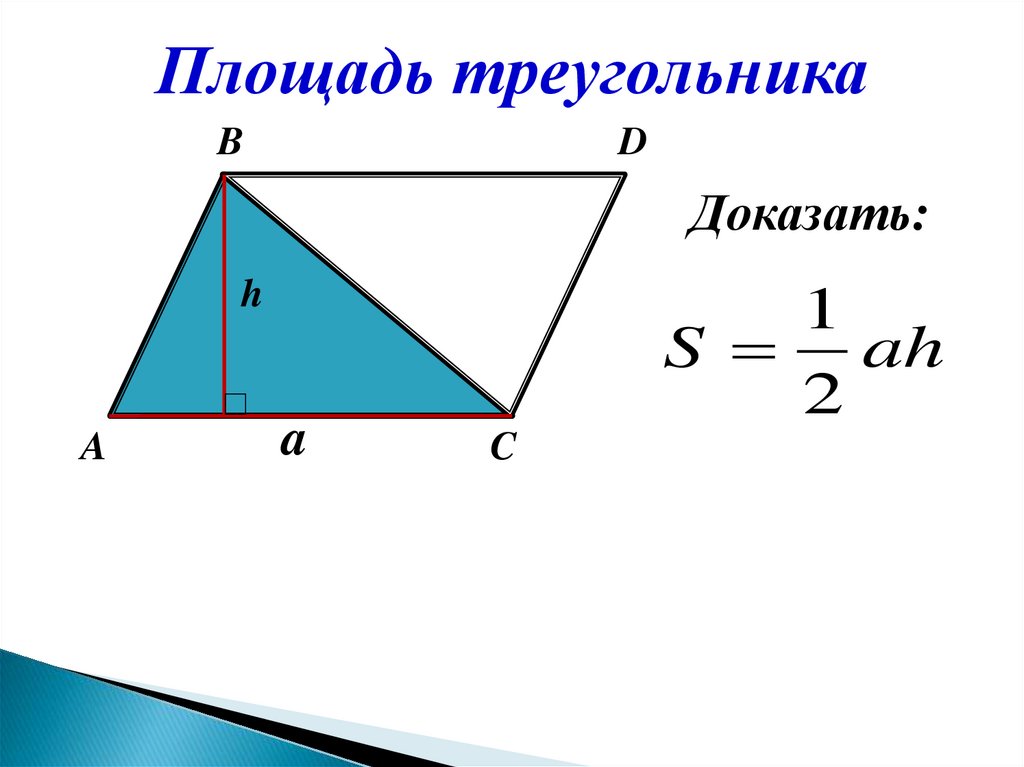
Площадь треугольникаB
D
Доказать:
h
A
a
1
S ah
2
C
19.
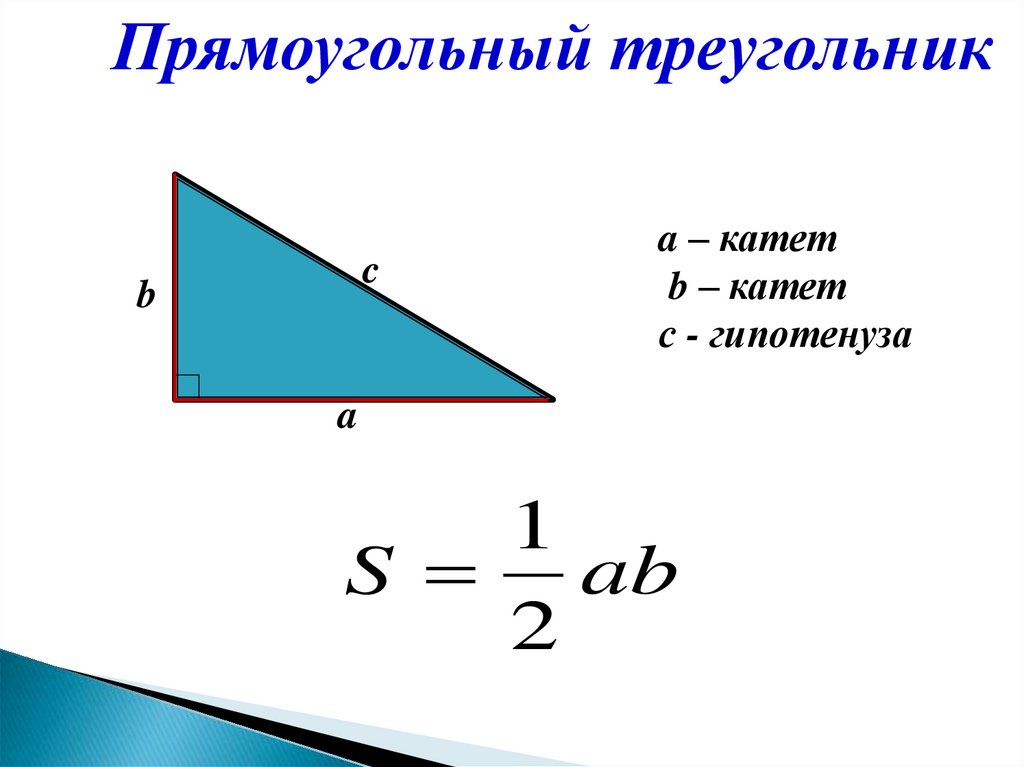
Прямоугольный треугольникc
b
a – катет
b – катет
с - гипотенуза
a
1
S ab
2
20.
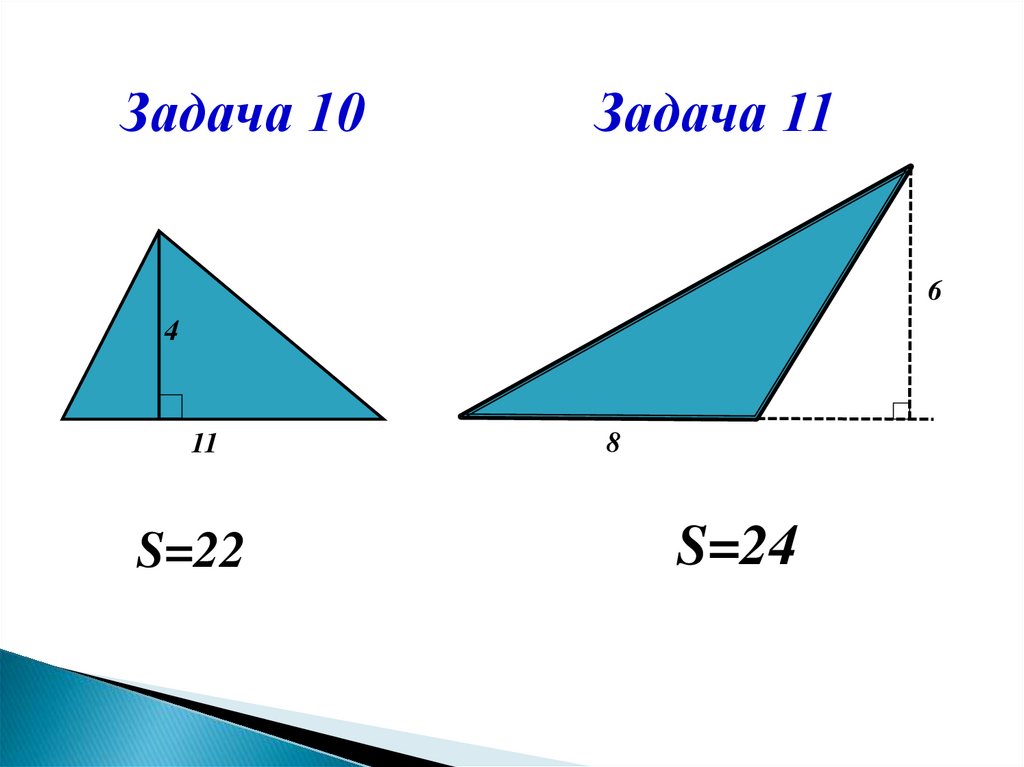
Задача 10Задача 11
6
4
11
S=22
8
S=24
21.
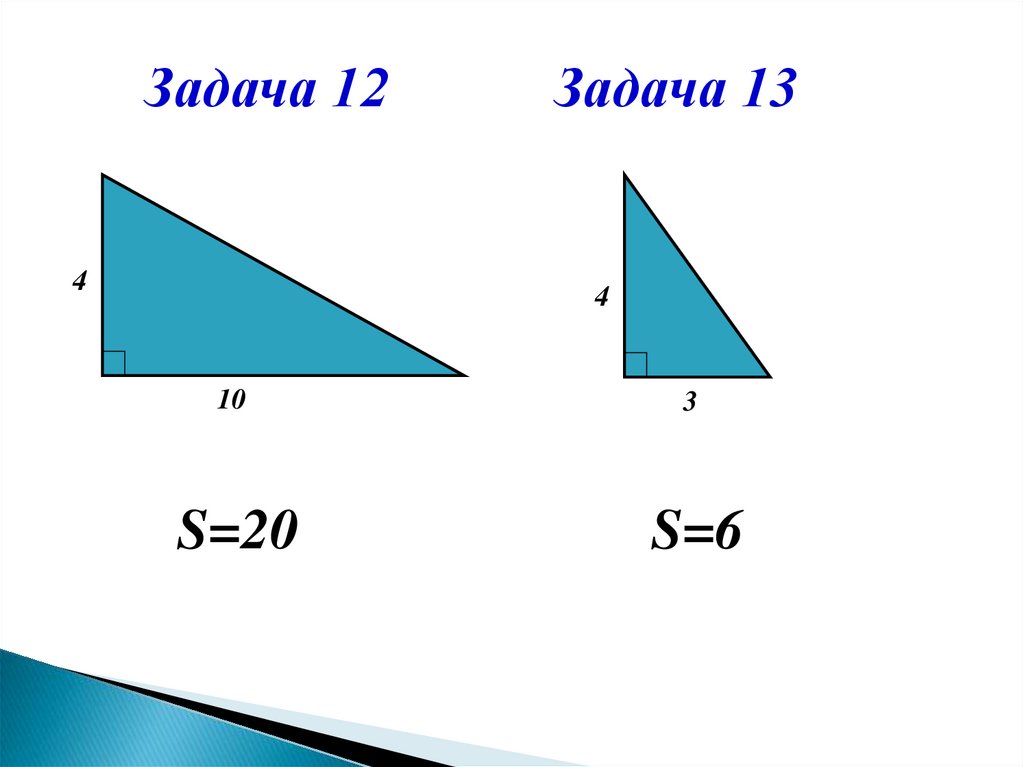
Задача 124
Задача 13
4
10
3
S=20
S=6
22.
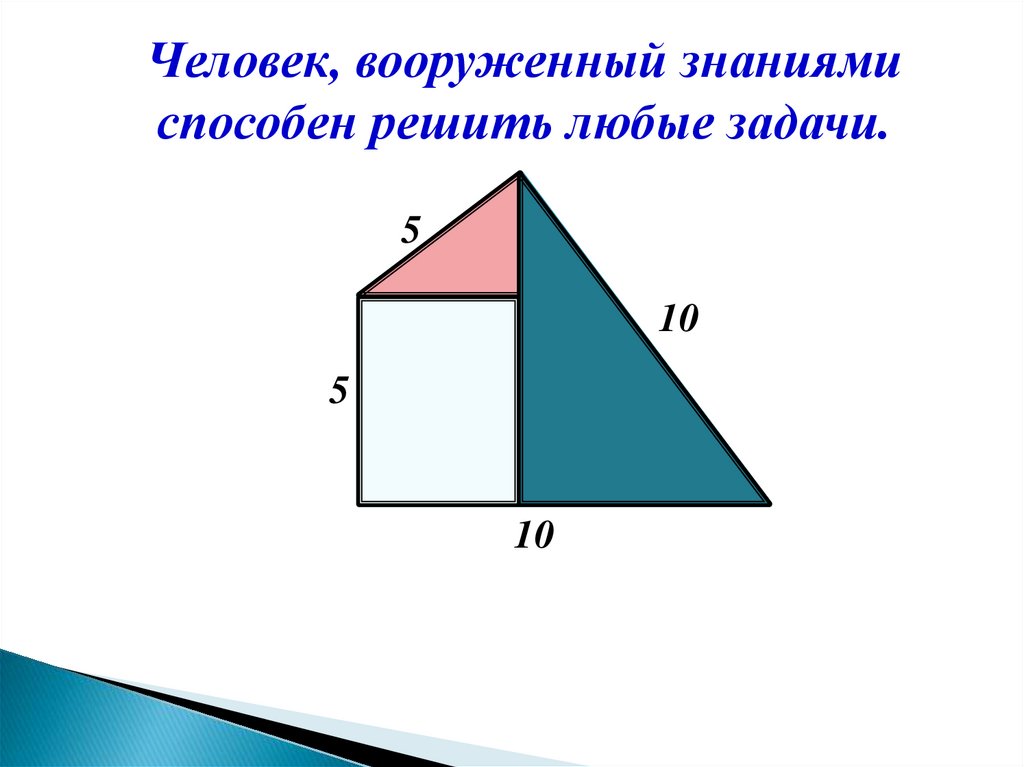
Человек, вооруженный знаниямиспособен решить любые задачи.
5
10
5
10
23.
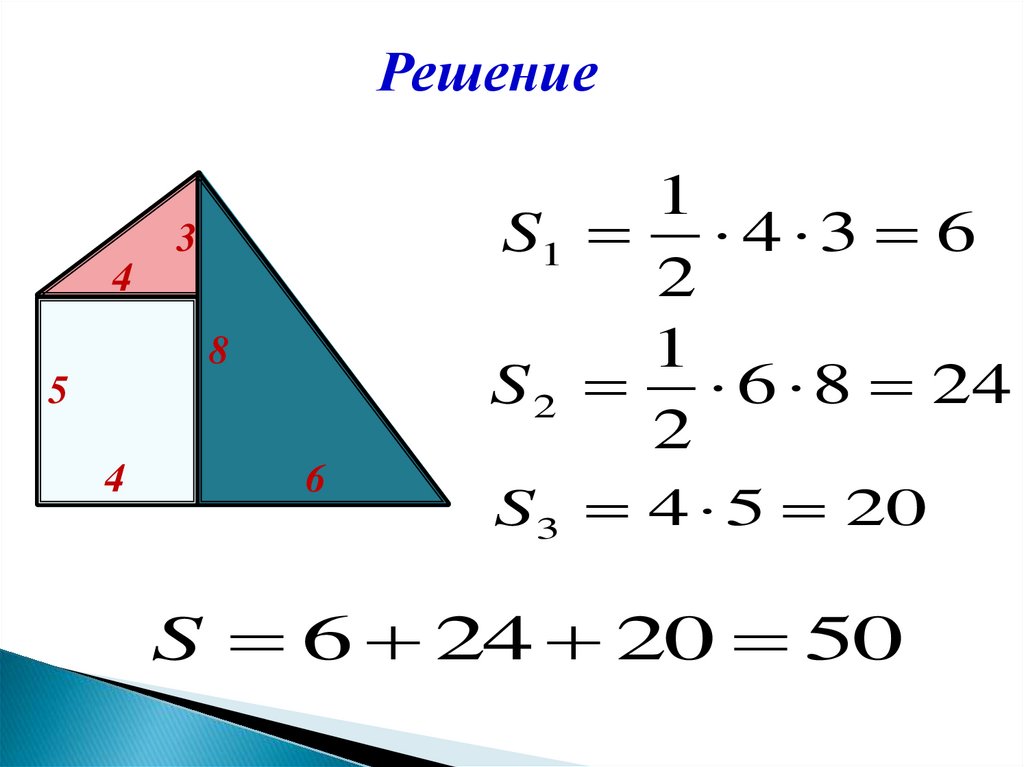
Решение1
S1 4 3 6
2
1
S 2 6 8 24
2
3
4
8
5
4
6
S3 4 5 20
S 6 24 20 50
24.
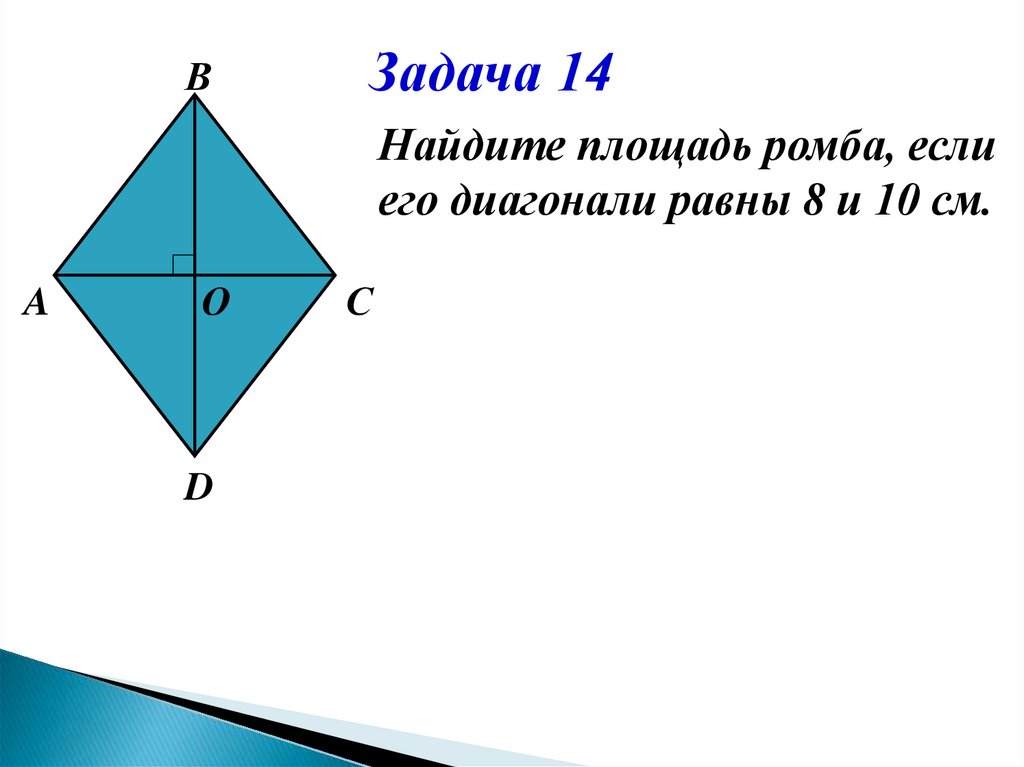
ВЗадача 14
Найдите площадь ромба, если
его диагонали равны 8 и 10 см.
A
О
D
С
25.
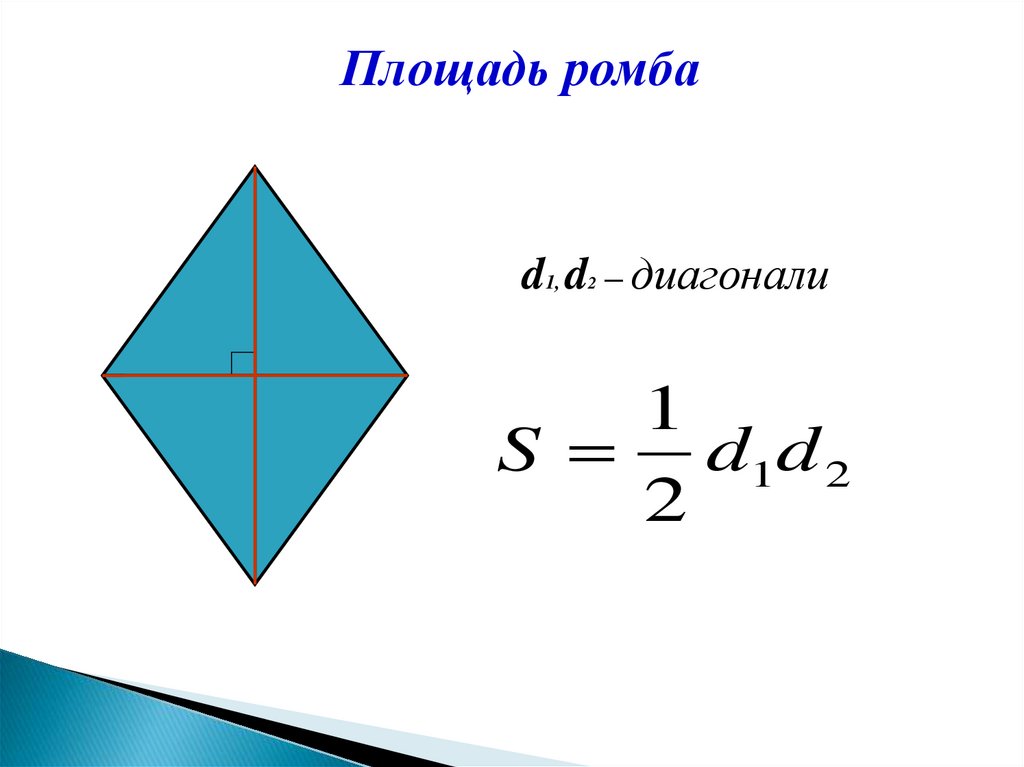
Площадь ромбаd1, d – диагонали
2
1
S d1d 2
2
26.
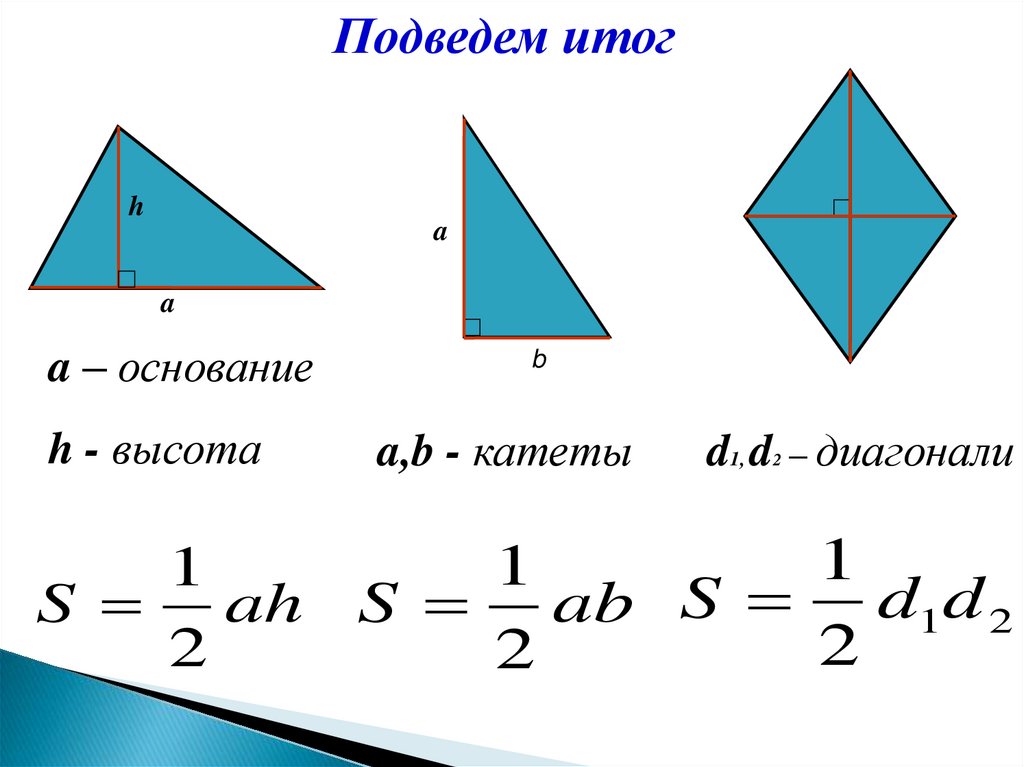
Подведем итогh
a
a
a – основание
h - высота
b
a,b - катеты
d1, d – диагонали
2
1
1
1
S ah S ab S d1d 2
2
2
2
27.
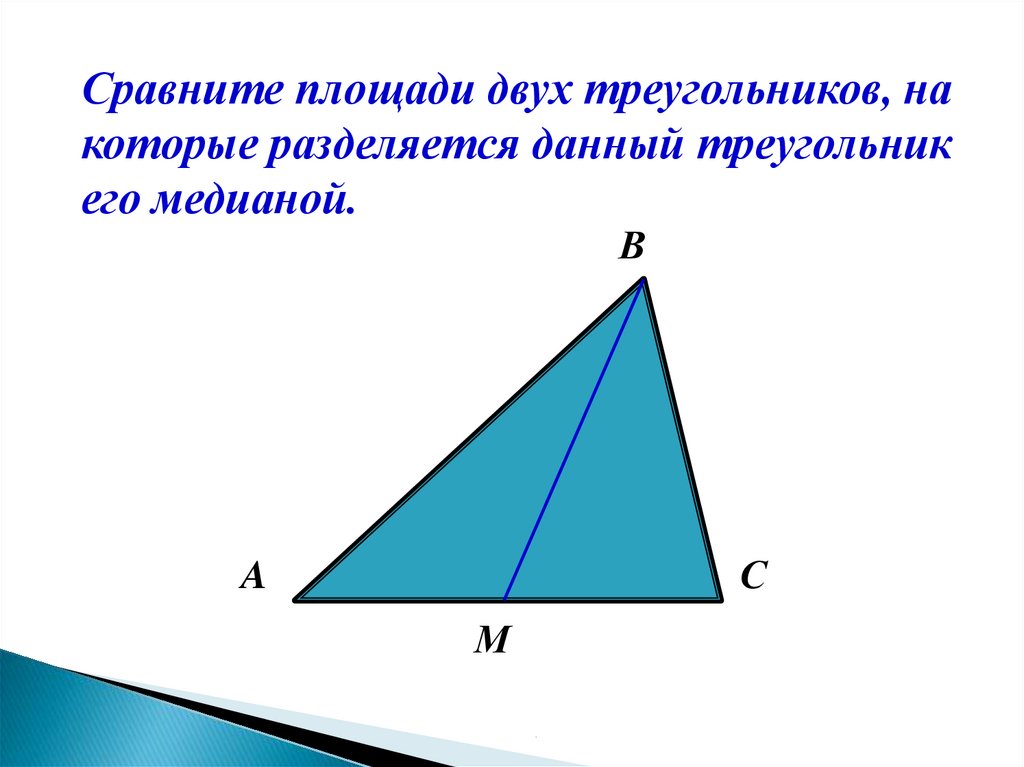
Сравните площади двух треугольников, накоторые разделяется данный треугольник
его медианой.
В
С
A
М
28.
Самостоятельная работаВариант 1
Вариант 2
№1
S= 16
№1
S= 35
№2
S= 44
№2
S= 60
№3
S= 21
№3
S= 20
29.
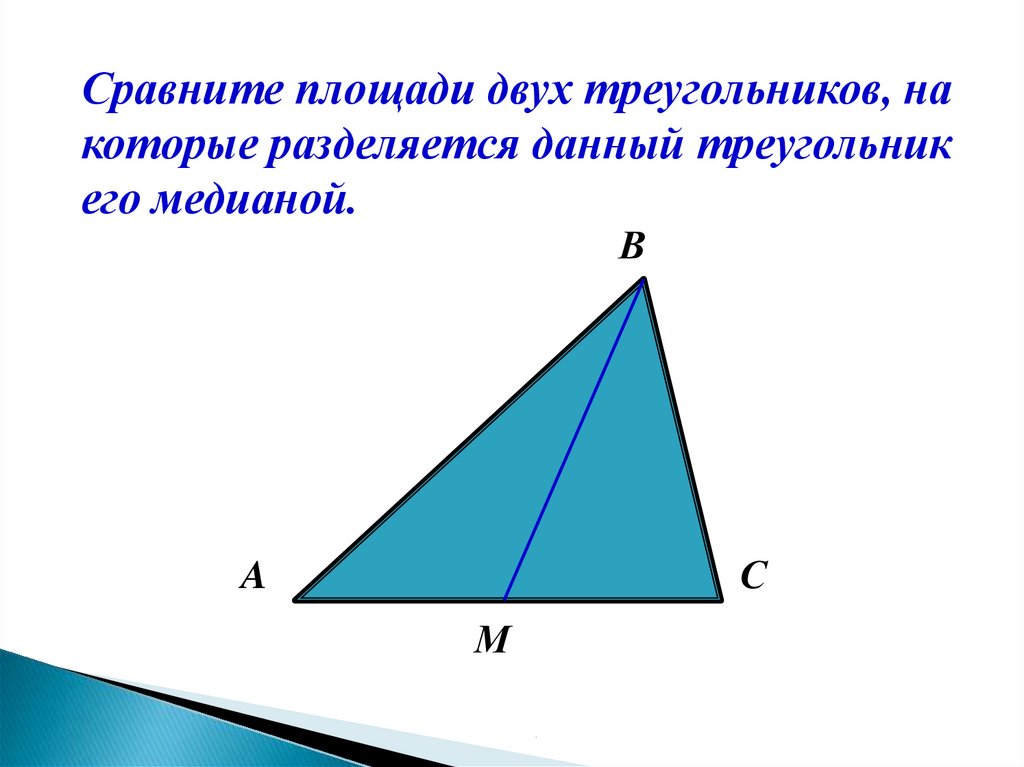
Сравните площади двух треугольников, накоторые разделяется данный треугольник
его медианой.
В
С
A
М
30.
Домашнее задание:• п.52 выучить формулировку и доказательство
теоремы о площади треугольника;
•№ 468(а,в), № 471, № 476;
•доказательство теоремы о площади ромба по
желанию.







 Математика
Математика








