Похожие презентации:
Окружность вписанная, описанная, вневписанная
1. Окружность вписанная, описанная, вневписанная
МАОУ «Лицей» г. БалашихаУчитель математики
Жирякова Л.В.
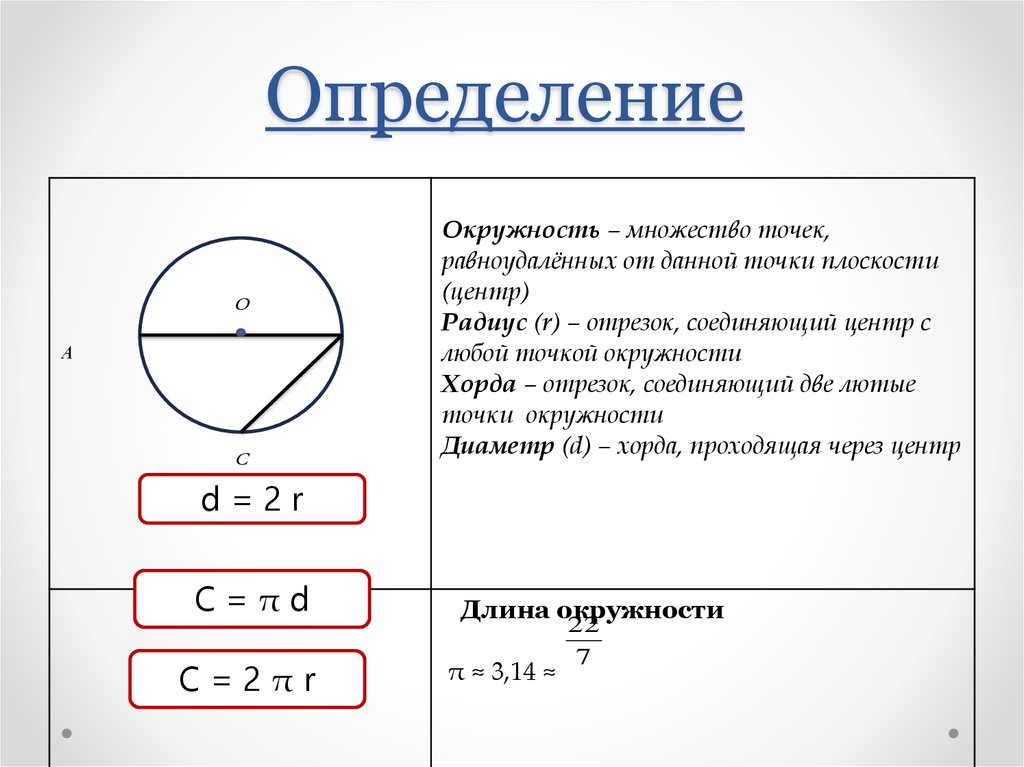
2. Определение
BO
A
C
Окружность – множество точек,
равноудалённых от данной точки плоскости
(центр)
Радиус (r) – отрезок, соединяющий центр с
любой точкой окружности
Хорда – отрезок, соединяющий две лютые
точки окружности
Диаметр (d) – хорда, проходящая через центр
d=2r
C=πd
C=2πr
Длина окружности
π ≈ 3,14 ≈
22
7
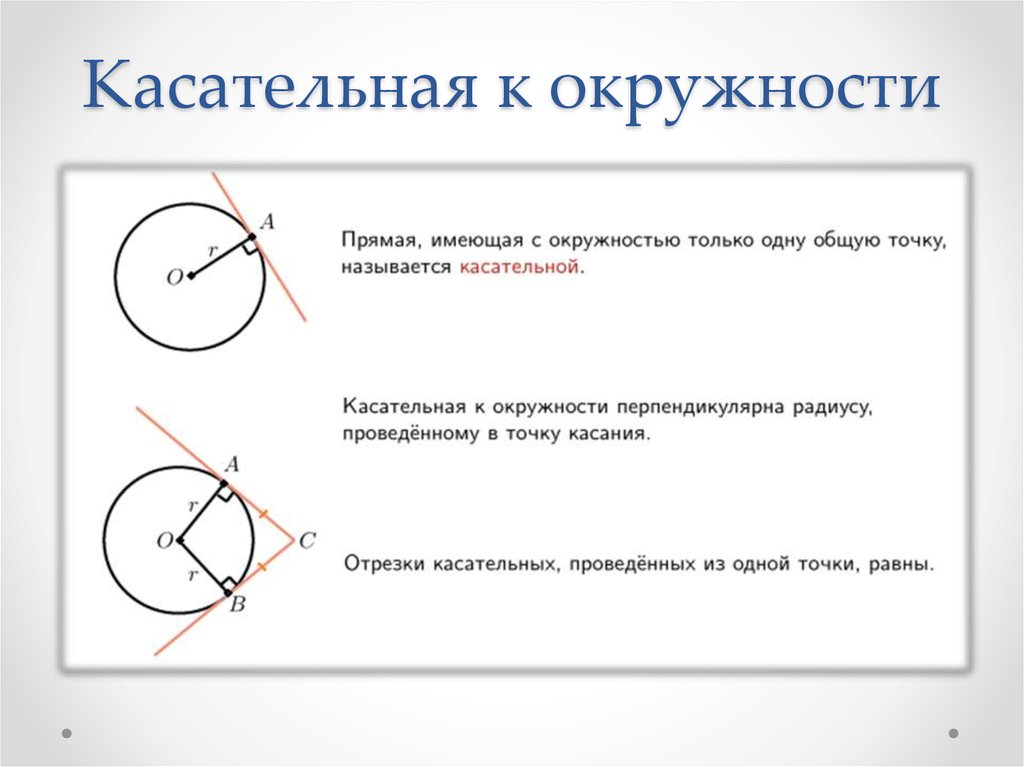
3. Касательная к окружности
4. Свойства хорд, секущих и касательных
AС
A
C
В
B
A
C B
А
С
E
D
D
D
B
AB CD хорды
АB ∩ CD = E
AC - касательная
F
AD - секущая
AF - секущая
AB – хорда
AC ∙ AD = AB ∙ AF
AE ∙ BE = CE ∙ DE
угол САВ
равен
половине дуги АВ
УголDAF
равен
полуразности
дугDF и CB
5.
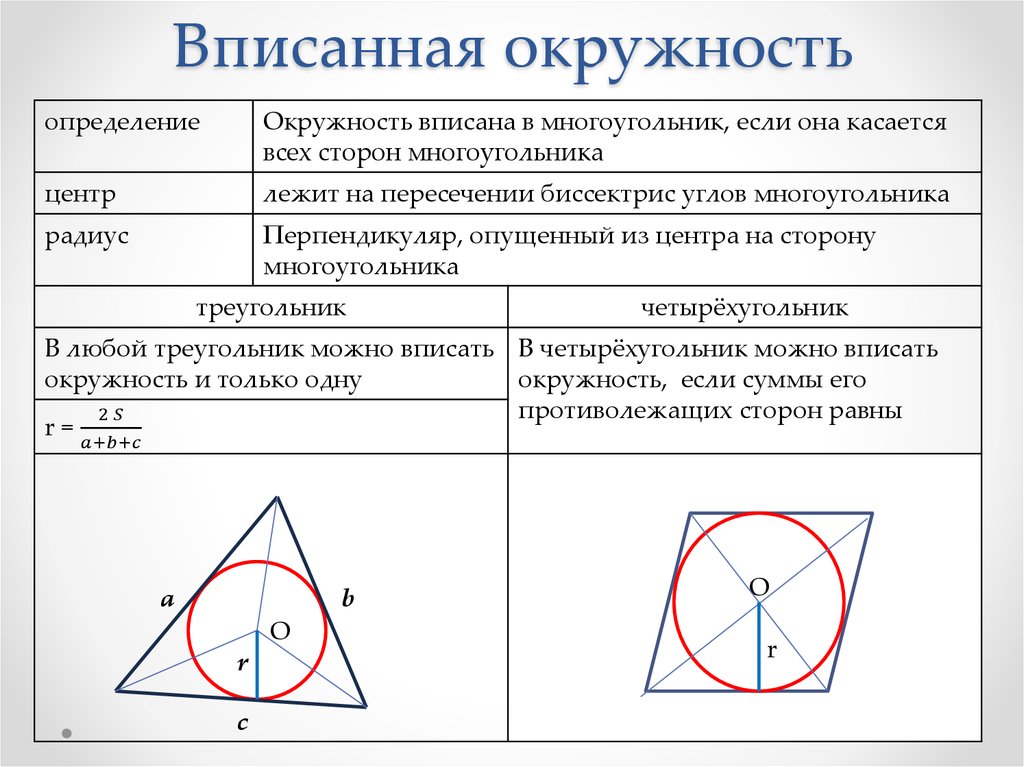
6. Вписанная окружность
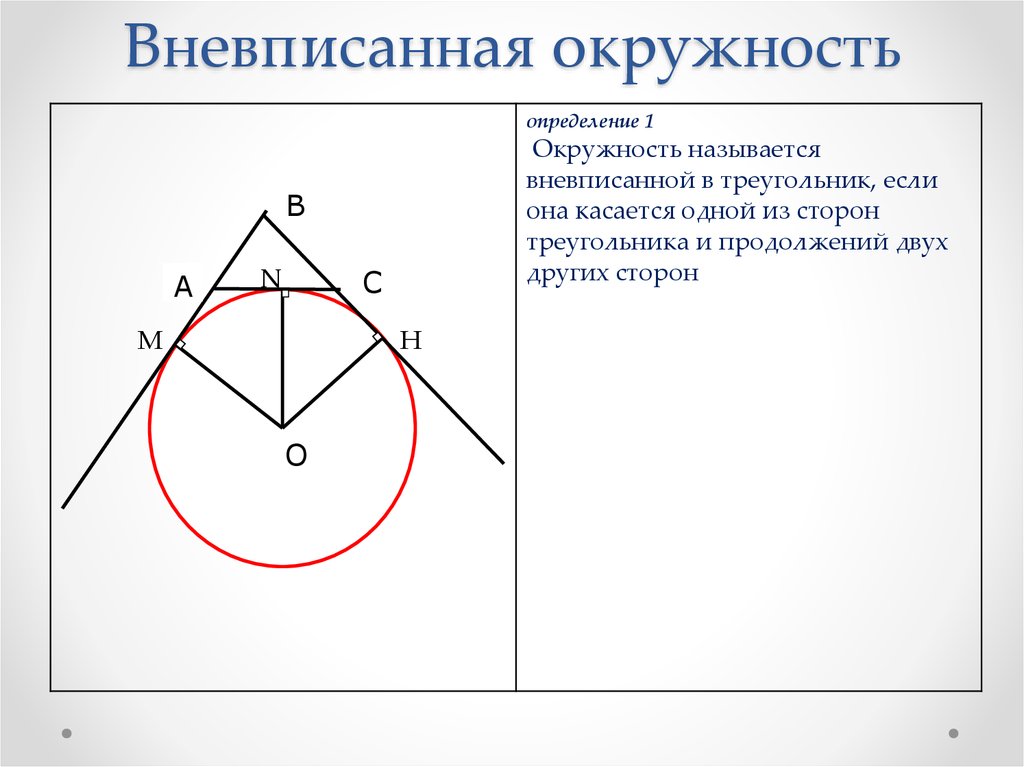
определениеОкружность вписана в многоугольник, если она касается
всех сторон многоугольника
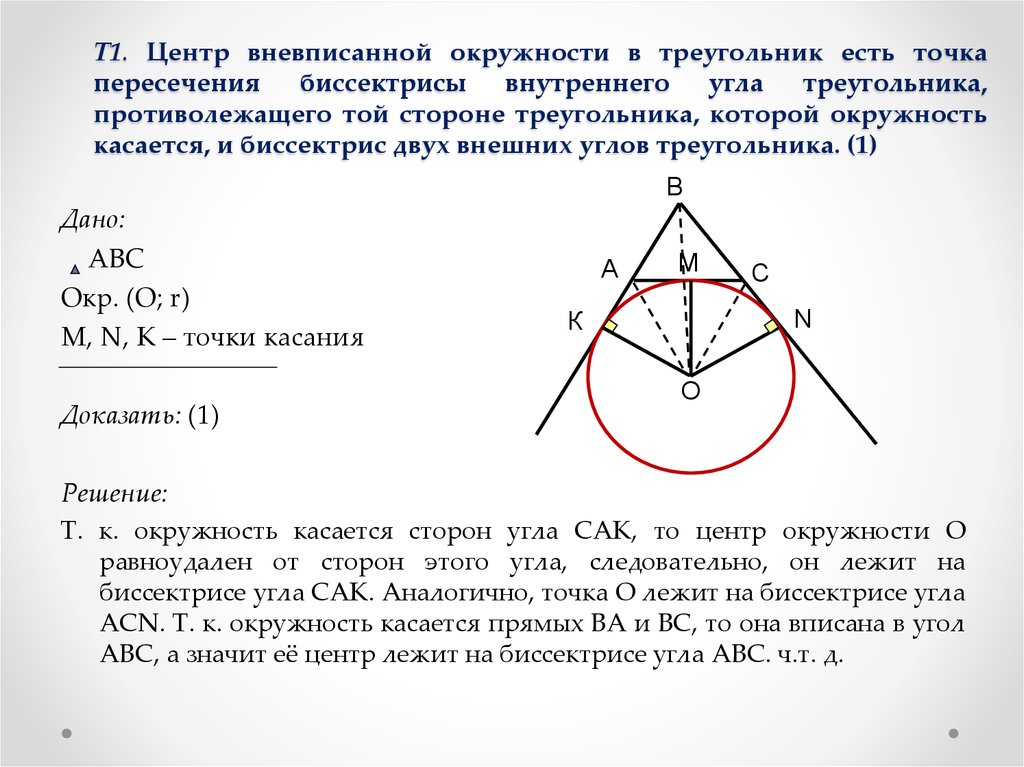
центр
лежит на пересечении биссектрис углов многоугольника
радиус
Перпендикуляр, опущенный из центра на сторону
многоугольника
треугольник
четырёхугольник
В любой треугольник можно вписать В четырёхугольник можно вписать
окружность и только одну
окружность, если суммы его
противолежащих сторон равны
2
















 Математика
Математика








