Множество решений неравенства с двумя переменными

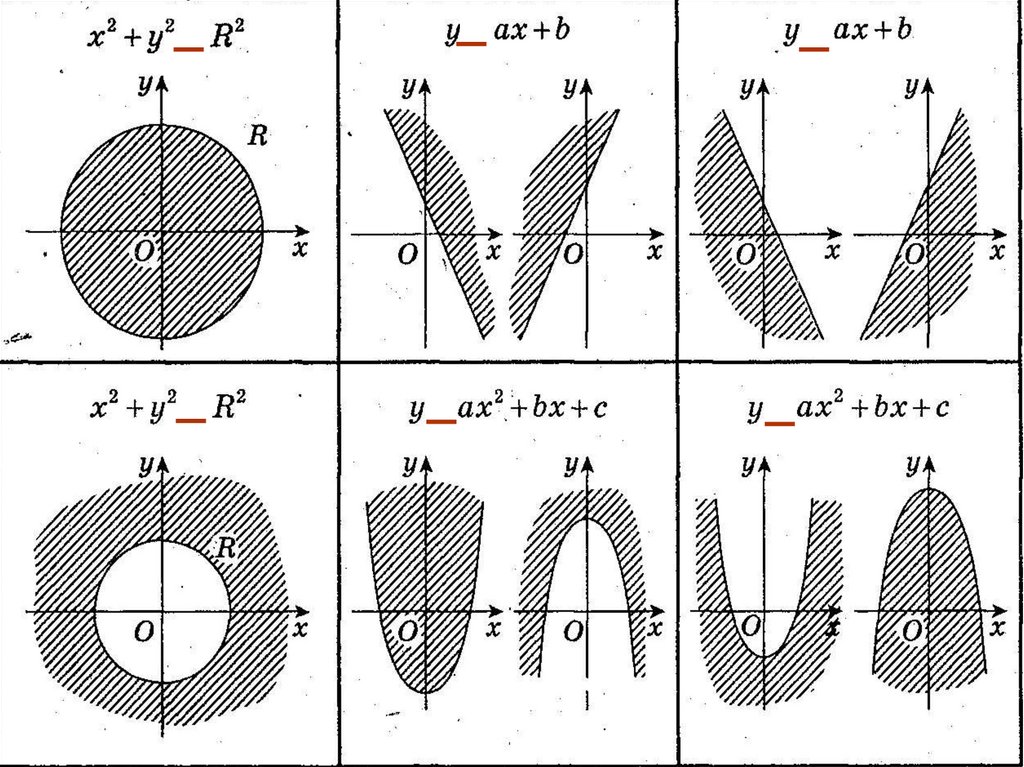
1.

2.

Множество решений неравенства с двумя
переменными
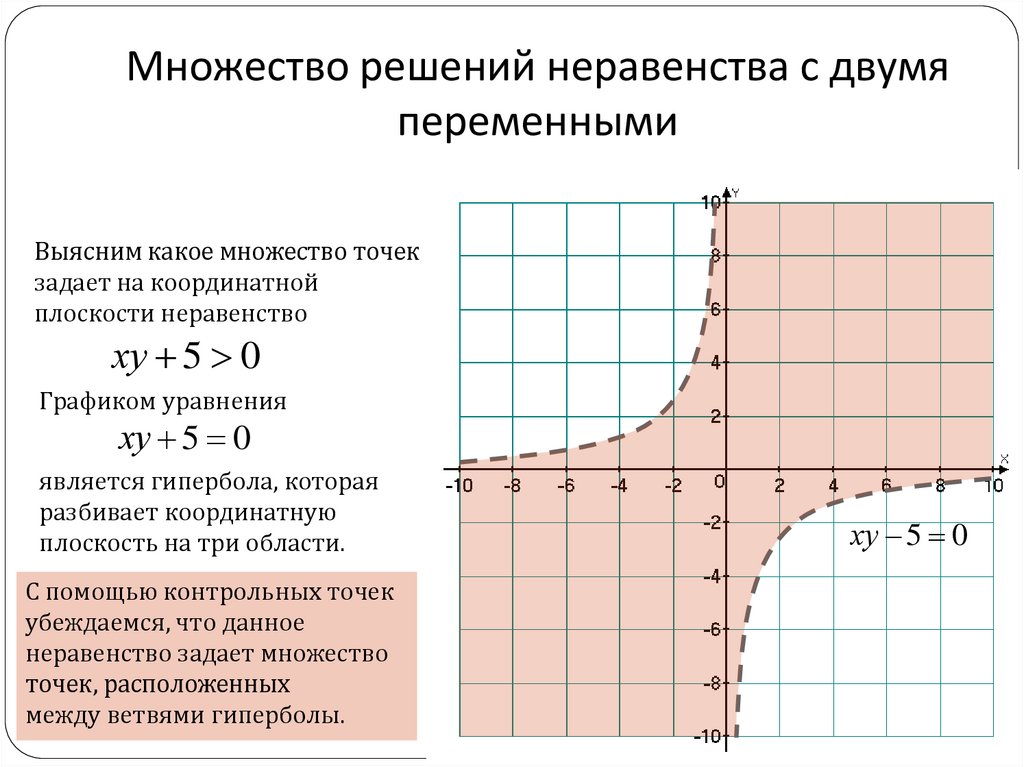
Выясним какое множество точек
задает на координатной
плоскости неравенство
ху 5 0
Графиком уравнения
ху 5 0
является гипербола, которая
разбивает координатную
плоскость на три области.
С помощью контрольных точек
убеждаемся, что данное
неравенство задает множество
точек, расположенных
между ветвями гиперболы.
ху 5 0

3.

Системы неравенств
с двумя переменными
К учебнику Ю.Н.Макарычева
Алгебра, 9 класс, Глава III §

4.

Решение системы неравенств
с двумя переменными
Решением системы неравенств с двумя переменными
называется
пара
значений
этих
переменных,
являющаяся как решением первого неравенства, так и
второго неравенства системы.
х у 2
у х 2
(1; 2) – решение ?
(2; 1) – решение ?
1 22 (верно)
2 1 2 (верно)
2 12 (неверно)
1 2 2 (верно)
(1; 2) – решение
(2; 1) –не решение

5.

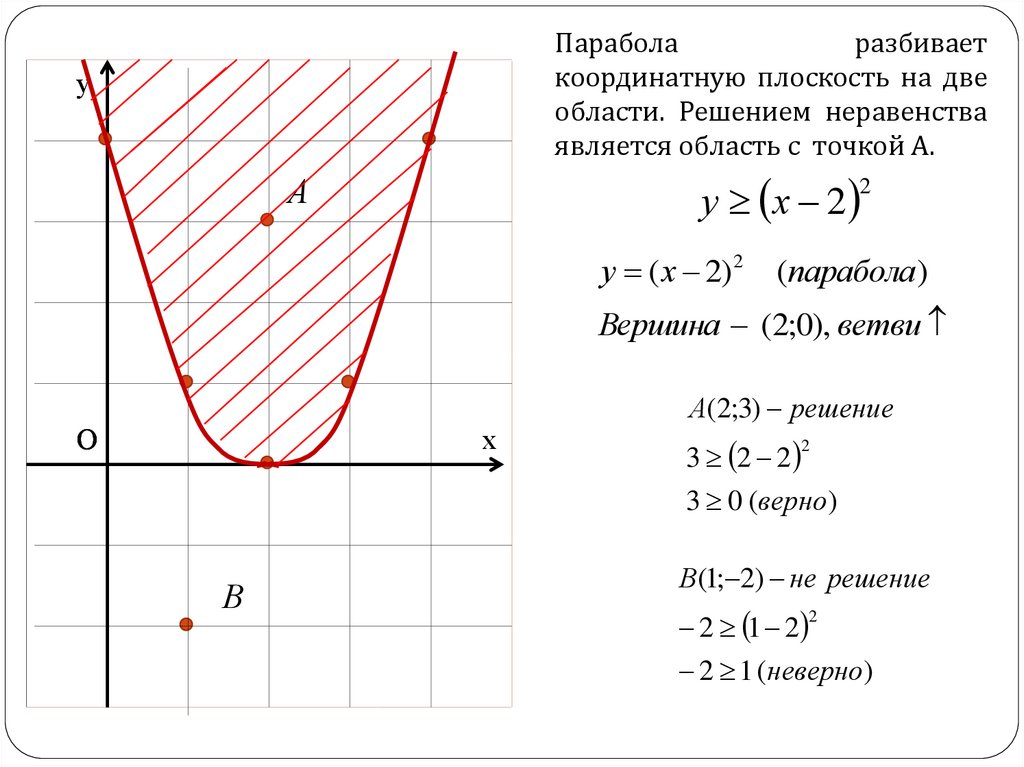
Изображение множества
Парабола
разбивает
решений неравенства
координатную
плоскость на двес
двумяРешением
переменными
на
области.
неравенства
координатной
плоскости
является
область с точкой
А.
у
у х 2
А
2
у ( х 2) 2
(парабола)
Вершина (2;0), ветви
О
х
А(2;3) решение
3 2 2
2
3 0 (верно)
В
В(1; 2) не решение
2 1 2
2
2 1 (неверно)

6.

Изображение
множества
решений системы неравенств
с двумя переменными на
координатной плоскости
Множеством
решений
системы
неравенств
с
двумя
переменными является пересечение множеств решений
неравенств, входящих в систему. На координатной плоскости
множество решений системы неравенств изображается
множеством точек, являющихся общей частью множеств,
представляющих собой решения каждого неравенства
системы.

7.

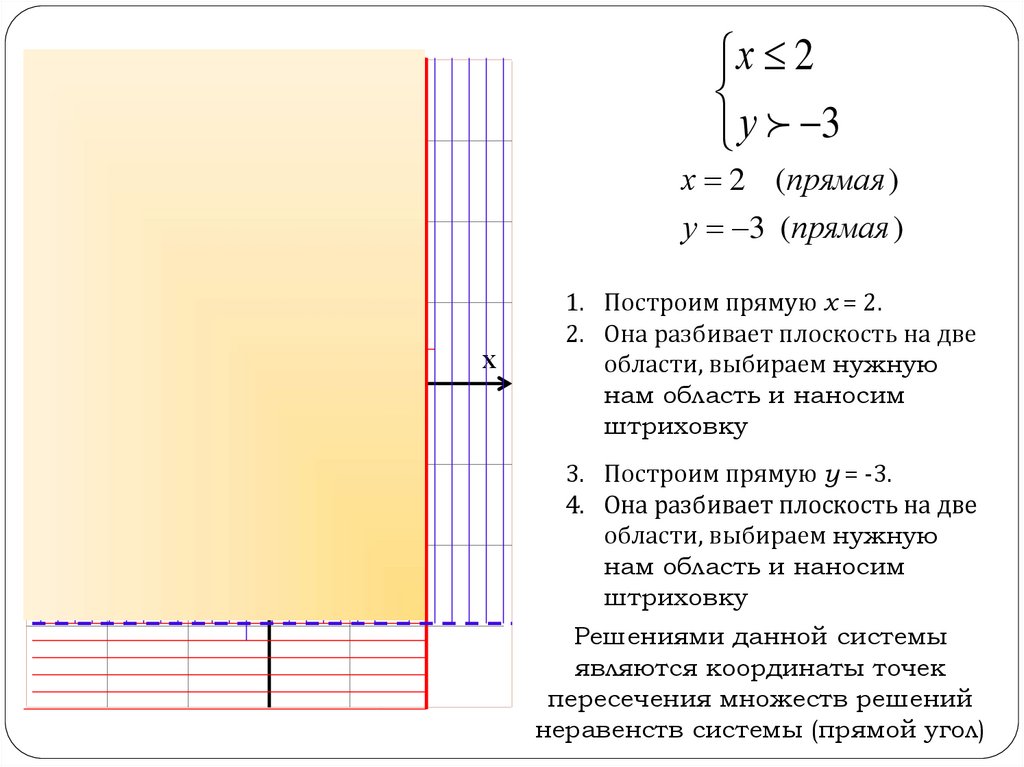
х 2
у 3
у
х 2 (прямая )
х =2
у 3 (прямая )
О
у = -3
х
1. Построим прямую х = 2.
2. Она разбивает плоскость на две
области, выбираем нужную
нам область и наносим
штриховку
3. Построим прямую у = -3.
4. Она разбивает плоскость на две
области, выбираем нужную
нам область и наносим
штриховку
Решениями данной системы
являются координаты точек
пересечения множеств решений
неравенств системы (прямой угол)

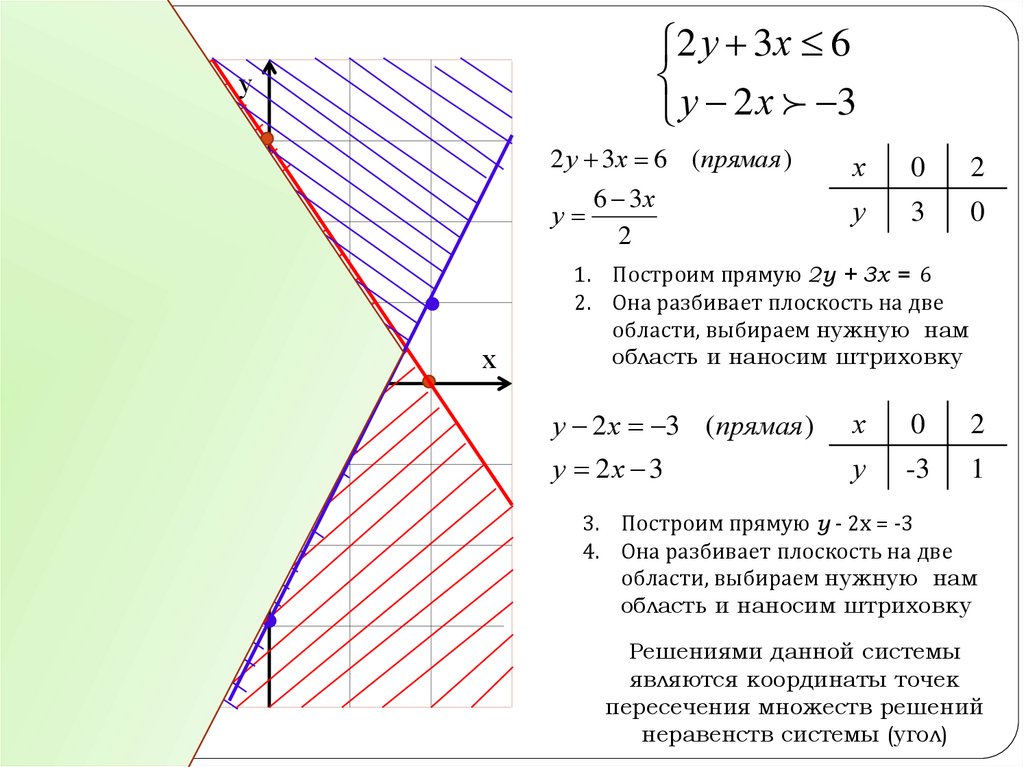
8.

2 у 3х 6
у 2 х 3
у
2 у 3х 6 (прямая )
у
О
х
6 3х
2
х
0
2
у
3
0
1. Построим прямую 2у + 3х = 6
2. Она разбивает плоскость на две
области, выбираем нужную нам
область и наносим штриховку
у 2 х 3 (прямая )
х
0
2
у 2х 3
у
-3
1
3. Построим прямую у - 2х = -3
4. Она разбивает плоскость на две
области, выбираем нужную нам
область и наносим штриховку
Решениями данной системы
являются координаты точек
пересечения множеств решений
неравенств системы (угол)

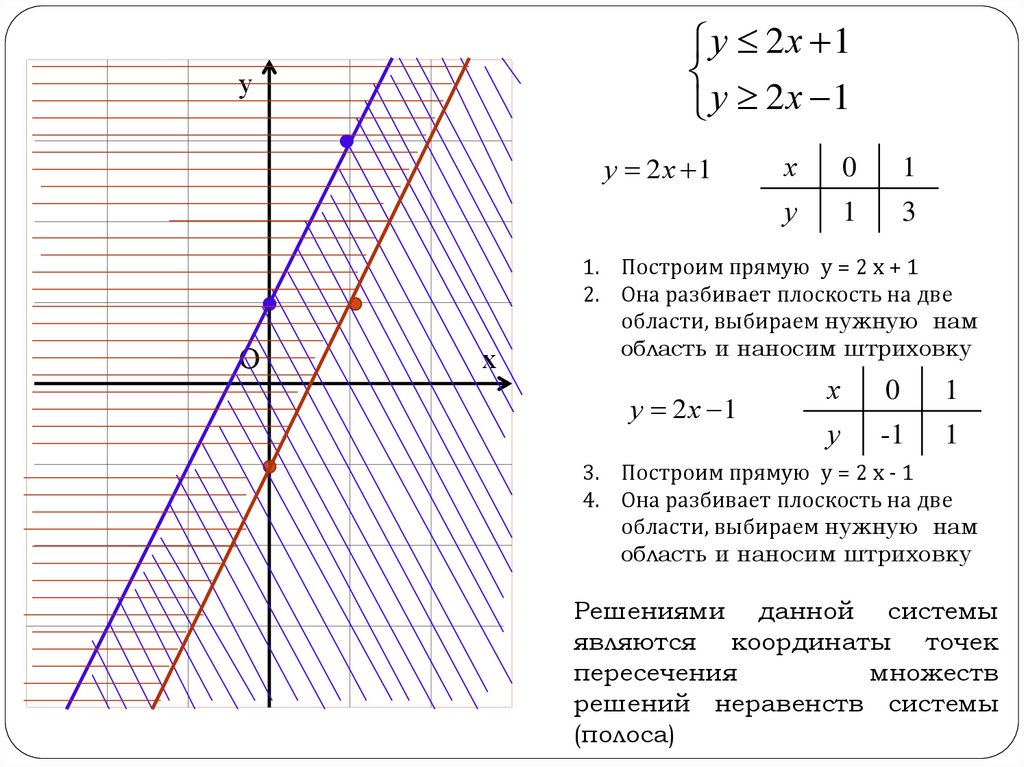
9.

у 2х 1
у 2х 1
у
у 2х 1
О
х
х
0
1
у
1
3
1. Построим прямую у = 2 х + 1
2. Она разбивает плоскость на две
области, выбираем нужную нам
область и наносим штриховку
у 2х 1
х
0
1
у
-1
1
3. Построим прямую у = 2 х - 1
4. Она разбивает плоскость на две
области, выбираем нужную нам
область и наносим штриховку
Решениями данной системы
являются координаты точек
пересечения
множеств
решений неравенств системы
(полоса)

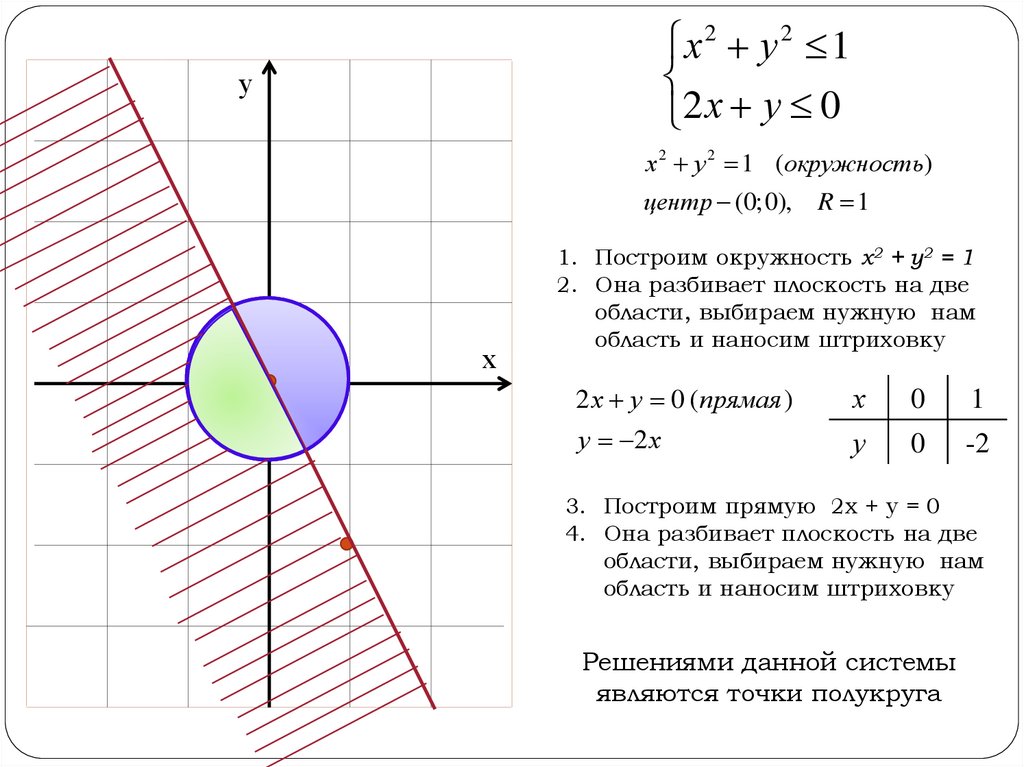
10.

х2 у 2 1
2 х у 0
у
х 2 у 2 1 (окружность)
центр (0; 0), R 1
О
х
1. Построим окружность х2 + у2 = 1
2. Она разбивает плоскость на две
области, выбираем нужную нам
область и наносим штриховку
2 х у 0 (прямая )
х
0
1
у 2 х
у
0
-2
3. Построим прямую 2х + у = 0
4. Она разбивает плоскость на две
области, выбираем нужную нам
область и наносим штриховку
Решениями данной системы
являются точки полукруга

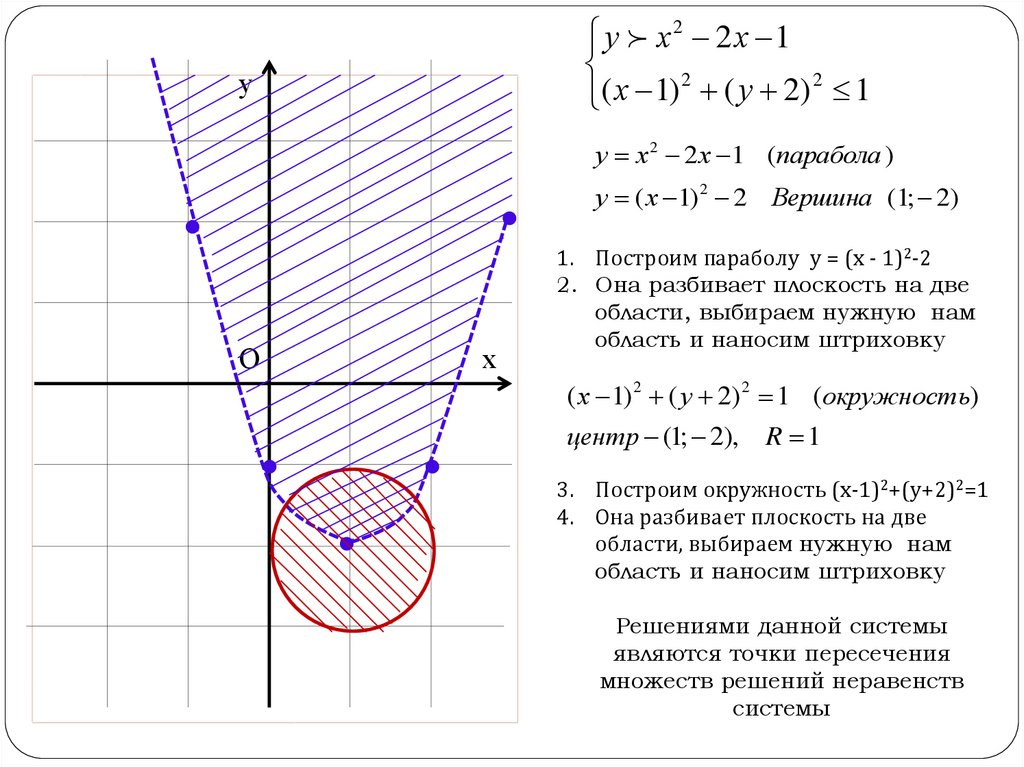
11.

у х 2 2 х 1
( х 1) 2 ( у 2) 2 1
у
у х 2 2 х 1 (парабола )
у ( х 1) 2 2 Вершина (1; 2)
О
х
1. Построим параболу у = (х - 1)2-2
2. Она разбивает плоскость на две
области, выбираем нужную нам
область и наносим штриховку
( х 1) 2 ( у 2) 2 1 (окружность)
центр (1; 2), R 1
3. Построим окружность (х-1)2+(у+2)2=1
4. Она разбивает плоскость на две
области, выбираем нужную нам
область и наносим штриховку
Решениями данной системы
являются точки пересечения
множеств решений неравенств
системы

12.

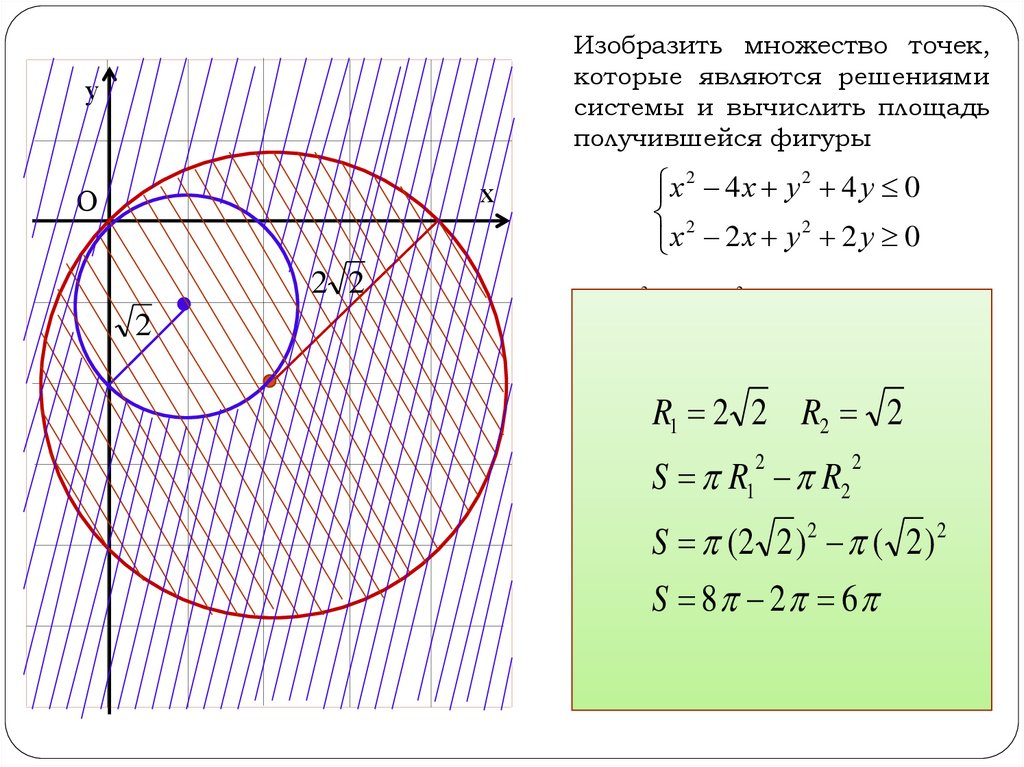
Изобразить множество точек,
которые являются решениями
системы и вычислить площадь
получившейся фигуры
у
х
О
2 2
2
х 2 4 х у 2 4 у 0
2
х 2 х у 2 2 у 0
х2 4х у2 4 у 0
х2 4х 4 4 у2 4 у 4 4 0
х2 4х 4 у2 4 у 4 8
2 2
2
(х R
12)
(у 2
2) 2 R
2(2 2 )2
2 ( 2; 2)2и R 2 2
Окр . с центром
S R1 R2
х 2 4 х у 2 4 у 2 0
S (2 2 ) ( 2 ) 2
х2 2х 1 1 у 2 2 у 1 1 0
х 2S
2 х8 1 у22
2
у 61 2
( х 1) 2 ( у 1) 2 ( 2 ) 2
Окр . с центром (1; 1) и R 2

13.

у
О
х