5-минутка ОГЭ. Вопросы

1.

5-минутка ОГЭ

2.

ВОПРОСЫ
1. Сколькими способами из 3-ех конфеток можем выбрать одну
2. Сколькими способами из 3-ех конфеток можем выбрать две
3. Сколькими способами можем 3-ех человек построить в ряд
4. Сколько диагоналей можно провести в треугольнике
5. Сколько диагоналей можно провести в четырехугольнике
6. Сколько диагоналей можно провести в пятиугольнике
7. Три человека играли в шахматы. Каждый с каждым сыграл по
одному разу. Сколько всего было партий
• 8. Четыре человека играли в шахматы. Каждый с каждым
сыграл по одному разу. Сколько всего было партий
• 9. Сколькими способами можно выбрать в нашем классе
старосту и его заместителя
• 10. Из пункта А в пункт В ведут три дороги, а из В в пункт С две
дороги. Сколькими способами можно добраться из А в С

3.

• Область математики, которая занимается
решением подобных задач, называется
• КОМБИНАТОРИКОЙ
• (комбинаторика выясняет, сколько
различных комбинаций, удовлетворяющих
определенному правилу, можно составить
из элементов данного множества)

4.

14.02 Классная работа
Основные правила комбинаторики

5.

ПЕРВОЕ ПРАВИЛО КОМБИНАТОРИКИ
• Пример1
• Туриста заинтересовали 5 маршрутов в
Карелии и 7 маршрутов на Кавказе.
Сколькими способами он может
организовать свой отпуск, имея время
только на один маршрут?

6.

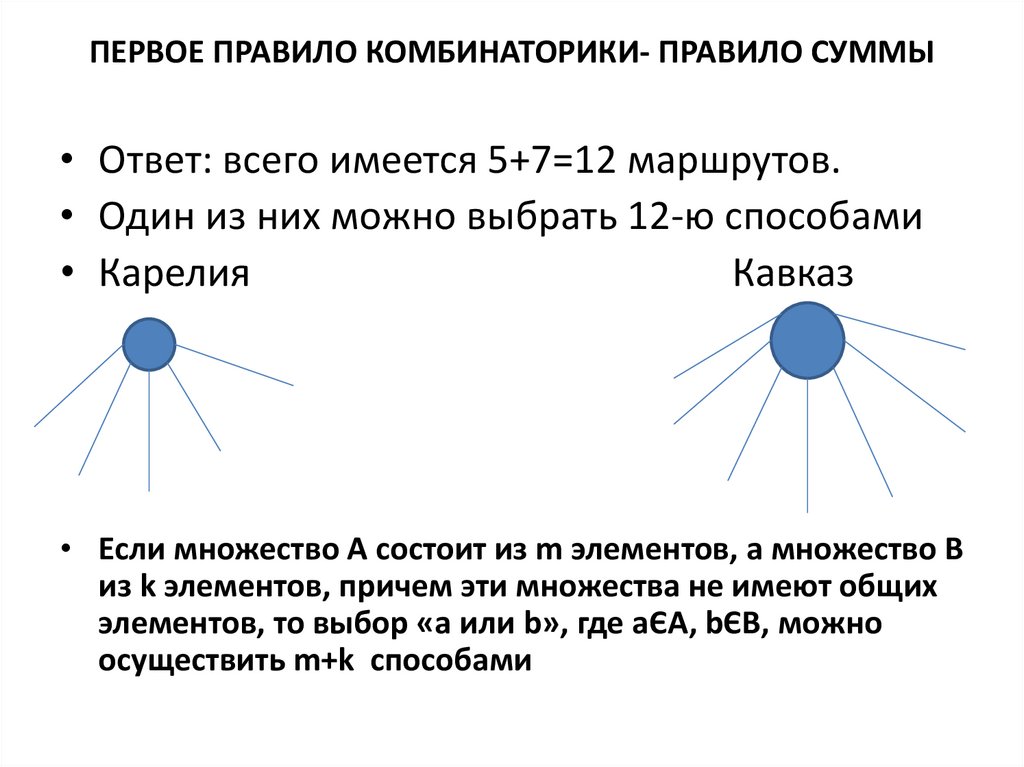
ПЕРВОЕ ПРАВИЛО КОМБИНАТОРИКИ- ПРАВИЛО СУММЫ
• Ответ: всего имеется 5+7=12 маршрутов.
• Один из них можно выбрать 12-ю способами
• Карелия
Кавказ
• Если множество А состоит из m элементов, а множество В
из k элементов, причем эти множества не имеют общих
элементов, то выбор «а или b», где аЄА, bЄВ, можно
осуществить m+k способами

7.

ВТОРОЕ ПРАВИЛО КОМБИНАТОРИКИ
• Пример 2
• Туриста заинтересовали 5 маршрутов в
Карелии и 7 маршрутов на Кавказе. Он
хочет побывать в Карелии и на Кавказе.
Сколькими способами он может
организовать свой отпуск, имея время на
два маршрута?

8.

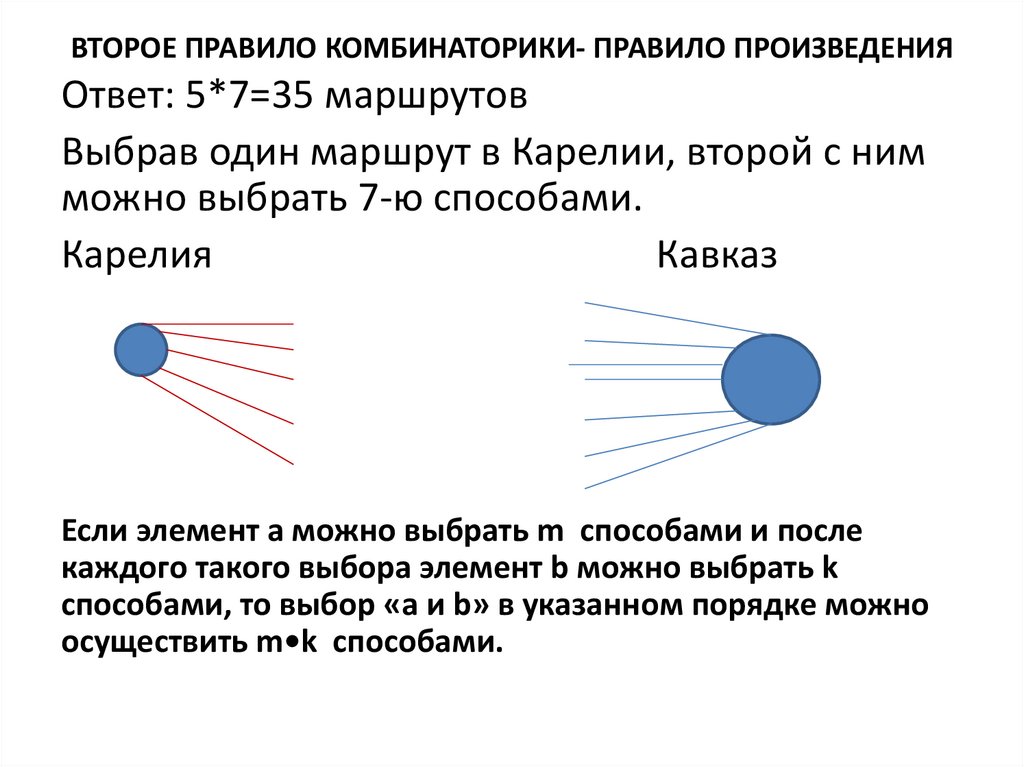
ВТОРОЕ ПРАВИЛО КОМБИНАТОРИКИ- ПРАВИЛО ПРОИЗВЕДЕНИЯ
Ответ: 5*7=35 маршрутов
Выбрав один маршрут в Карелии, второй с ним
можно выбрать 7-ю способами.
Карелия
Кавказ
Если элемент а можно выбрать m способами и после
каждого такого выбора элемент b можно выбрать k
способами, то выбор «а и b» в указанном порядке можно
осуществить m•k способами.