Плоскопараллельное движение твёрдого тела

1.

Тема 12.
ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЁРДОГО ТЕЛА.
12.1. УРАВНЕНИЕ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ.
Плоскопараллельным (или плоским) называется такое
движение твердого тела, при котором все его точки
перемещаются параллельно некоторой
фиксированной плоскости П.
Плоское движение совершают многие
части механизмов и машин, например
катящееся колесо на прямолинейном
участке пути, шатун в
кривошипно-ползунном механизме и др.
Частным случаем плоскопараллельного
движения является вращательное
движение твердого тела вокруг
неподвижной оси.

2.

12.1. УРАВНЕНИЕ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ.
Положение фигуры S в плоскости
Оху определяется положением
какого-нибудь проведенного на
этой фигуре отрезка АВ.
В свою очередь положение отрезка АВ можно определить,
зная координаты хА, уА точки А и угол , который отрезок АВ
образует с осью х. Точку А , выбранную для определения
положения фигуры S, будем в дальнейшем называть
полюсом.
При движении фигуры величины хА, уА и будут
изменяться.
Зависимости xA f1 t , yA f 2 t , f3 t будут
определять положение фигуры в плоскости Oxy.
2

3.

12.1. УРАВНЕНИЕ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ.
xA f1 t , yA f 2 t , f3 t
Эти уравнения называются уравнениями движения
плоской фигуры в ее плоскости. Они же являются
уравнениями плоскопараллельного движения
твердого тела.
Движение плоской фигуры в ее плоскости может
рассматриваться как слагающееся из поступательного
движения, при котором все точки фигуры движутся так же, как
полюс А, и из вращательного движения вокруг этого полюса.
Основными кинематическими характеристиками такого движения
являются скорость и ускорение поступательного движения полюса
( пост А ; апост аА . ), а также угловая скорость и угловое
ускорение вращательного движения вокруг полюса. Значения этих
характеристик в любой момент времени t можно найти, из уравнений
плоскопараллельного движения твёрдого тела.
Вращательная часть движения от выбора полюса не зависит.

4.

12.2. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ.
Рассмотрим точку М плоской фигуры,
положение которой определяется
расстоянием b=АМ от полюса А и углом
ВАМ = .
Если движение задано уравнениями
xA f1 t , yA f 2 t , f3 t ,
то координаты x и у точки М в осях Оху
будут:
x xA b cos , y y A b sin
Обычное уравнение траектории получим, исключив из
системы этих уравнений время t.
Если рассматривается движение звена какого-нибудь механизма, то для
определения траектории любой точки этого звена достаточно выразить
ее координаты через какой-нибудь параметр, определяющий положение
4
механизма, а затем исключить этот параметр.

5.

12.2. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ.
Ползуны А и В, к которым прикрепляется линейка
эллипсографа,
перемещаются
по
взаимно
перпендикулярным направляющим. Расстояние АВ=l.
Определить траекторию точки М линейки.
Решение:
1. Взяв за полюс точку А, будем определять
положение точки М на линейке отрезком АМ=b.
2. Положение самой линейки задается углом .
Тогда для координат х и у точки М получим:
x b l cos , y b sin .
3. Исключая параметр , находим, что
траекторией точки будет эллипс с центром в т.
О и полуосями a = b – l и b
x2
y2
2 1
2
b l b
5

6.

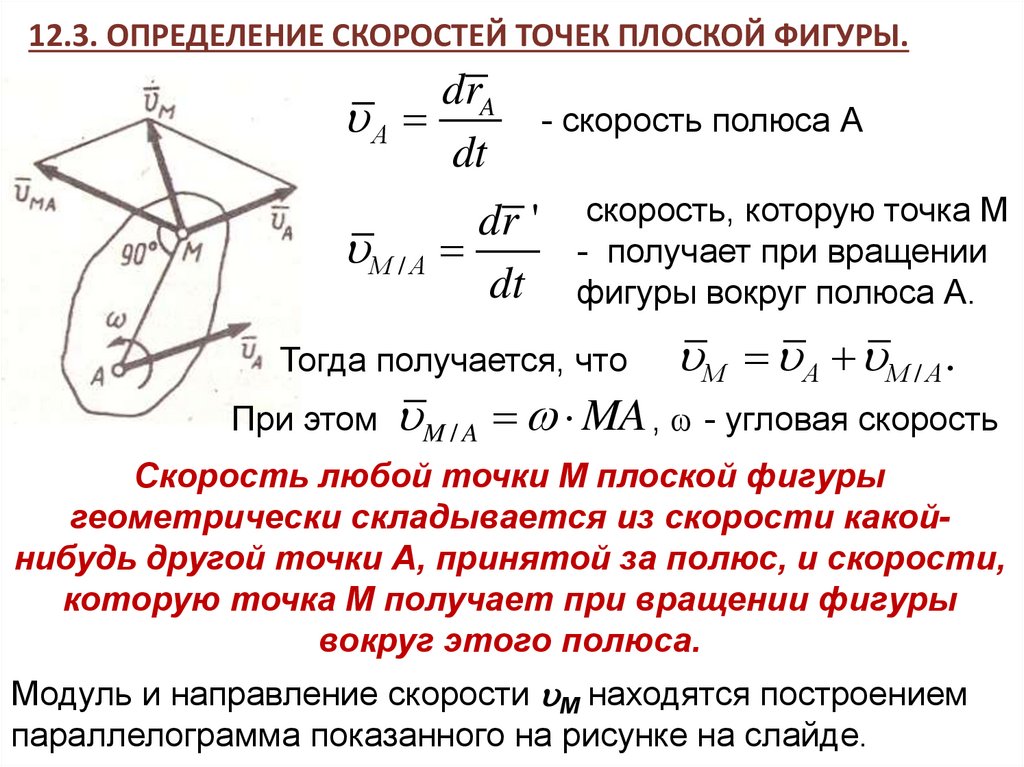
12.3. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ.
Движение плоской фигуры можно
рассматривать как слагающееся из
поступательного движения, при
котором все точки фигуры движутся
со скоростью полюса А ( A), и из
вращательного движения вокруг этого
полюса.
Положение любой точки М фигуры определяется по
отношению к осям Оху радиусом-вектором r r r '
A
rA - радиус-вектор полюса;
r ' AM - вектор, определяющий положение точки М
относительно осей Ах'у', перемещающихся вместе с полюсом
А поступательно.
Тогда:
dr drA dr
М
.
dt
dt
dt
6

7.

12.3. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ.
drA
А
dt
dr '
М / А
dt
- скорость полюса А
скорость, которую точка М
- получает при вращении
фигуры вокруг полюса А.
Тогда получается, что
М А М / A .
При этом M / A MA , - угловая скорость
Скорость любой точки М плоской фигуры
геометрически складывается из скорости какойнибудь другой точки А, принятой за полюс, и скорости,
которую точка М получает при вращении фигуры
вокруг этого полюса.
Модуль и направление скорости M находятся построением
параллелограмма показанного на рисунке на слайде.

8. Найти скорость точки М обода колеса, катящегося по прямолинейному рельсу без скольжения, если скорость центра С колеса равна ,

12.3. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ.
Найти скорость точки М обода колеса, катящегося по
прямолинейному рельсу без скольжения, если скорость
центра С колеса равна С , а угол DKM=
Решение:
М С МС
Скорость точки С известна,
примем её за полюс.
МС МС R
В данный момент времени
К 0
С другой стороны, так же
как и для точки М
К С КС
Так как скорости КС и
С
КС КС R
направлены вдоль одной прямой, то при
K 0 КC С откуда C / R. В результате MC R C .
Параллелограмм, построенный на векторах
МС и С
будет ромбом.
По свойствам ромба, так как диагонали ромба взаимно перпендикулярны,
получим 2 cos и К М
M
C
М

9.

12.4. ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛА.
Следствием из теоремы об определении скоростей точек
плоской фигуры М А М / A является теорема о
проекциях скоростей двух точек тела.
Проекции скоростей двух точек твердого тела на
ось, проходящую через эти точки, равны друг другу.
Для случая, изображённого
на рисунке
B
A
BA
Отсюда, проектируя обе части
равенства на ось, направленную по АВ, и учитывая, что
вектор BA перпендикулярен АВ', находим
B cos A cos
9

10.

12.5. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С
ПОМОЩЬЮ МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ (МЦС).
Мгновенным центром скоростей называется точка
плоской фигуры, скорость которой в данный момент
времени равна нулю.
Если фигура движется не поступательно, то такая
точка в каждый момент времени t существует и
притом единственная.
Пусть в момент времени t точки А и В плоской
фигуры имеют скорости A и В, не параллельные друг другу.
Тогда точка Р , лежащая на пересечении перпендикуляров к вектору A и к вектору В, и будет мгновенным
центром скоростей.
Если в момент времени t взять точку Р за полюс, то по теореме об
определении скоростей плоской фигуры, скорость точки А будет
А Р Р / A Р / A , т.к. Р 0
Аналогичный результат получается для любой другой точки фигуры.

11.

12.5. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С
ПОМОЩЬЮ МГНОВЕННОГОЦЕНТРА СКОРОСТЕЙ (МЦС).
Скорости точек плоской фигуры определяются в
данный момент времени так, как если бы движение
фигуры было вращением вокруг мгновенного центра
скоростей.
А РА ( А РА)
При этом
В РВ ( В РВ) и т.д.
Скорости точек плоской фигуры
пропорциональны их расстояниям
от мгновенного центра скоростей.
А
РА
В
РВ
Полученные результаты приводят к следующим выводам:
1. Для определения мгновенного центра скоростей надо знать
только направления скоростей A и В каких-нибудь двух точек А к
В плоской фигуры.
Мгновенный центр скоростей находится в точке пересечения перпендикуляров,
восставленных из точек А и В к скоростям этих точек (или к касательным к
траекториям).

12.

12.5. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С
ПОМОЩЬЮ МГНОВЕННОГОЦЕНТРА СКОРОСТЕЙ (МЦС).
Полученные результаты приводят к следующим выводам:
2. Для определения скорости любой точки плоской фигуры надо
знать модуль и направление скорости какой-нибудь одной точки
А фигуры и направление скорости другой ее точки В.
Тогда, восставив из точек А и В перпендикуляры к A и В, построим
мгновенный центр скоростей Р и по направлению A определим
направление поворота фигуры. После этого, зная A , найдем скорость
М любой точки М плоской фигуры. Направлен вектор М
перпендикулярно РМ в сторону поворота фигуры.
3. Угловая скорость плоской фигуры равна в каждый данный
момент времени отношению скорости какой-нибудь точки
фигуры к ее расстоянию от мгновенного центра скоростей Р:
В
РВ
(1),
В А
АВ
(2).
Когда A = 0 (точка А — мгновенный центр скоростей), формула (2)
переходит в (1).
12

13.

12.5. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С
ПОМОЩЬЮ МГНОВЕННОГОЦЕНТРА СКОРОСТЕЙ (МЦС).
Рассмотрим некоторые частные случаи определения мгновенного
центра скоростей.
а) Если плоскопараллельное движение осуществляется
путем качения без скольжения одного цилиндрического
тела по поверхности другого неподвижного, то точка Р
катящегося тела, касающаяся неподвижной поверхности,
имеет в данный момент времени скорость, равную нулю
( Р =0), и является мгновенным центром скоростей.
Примером служит качение колеса по рельсу.

14.

12.5. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С
ПОМОЩЬЮ МГНОВЕННОГОЦЕНТРА СКОРОСТЕЙ (МЦС).
Рассмотрим некоторые частные случаи определения мгновенного
центра скоростей.
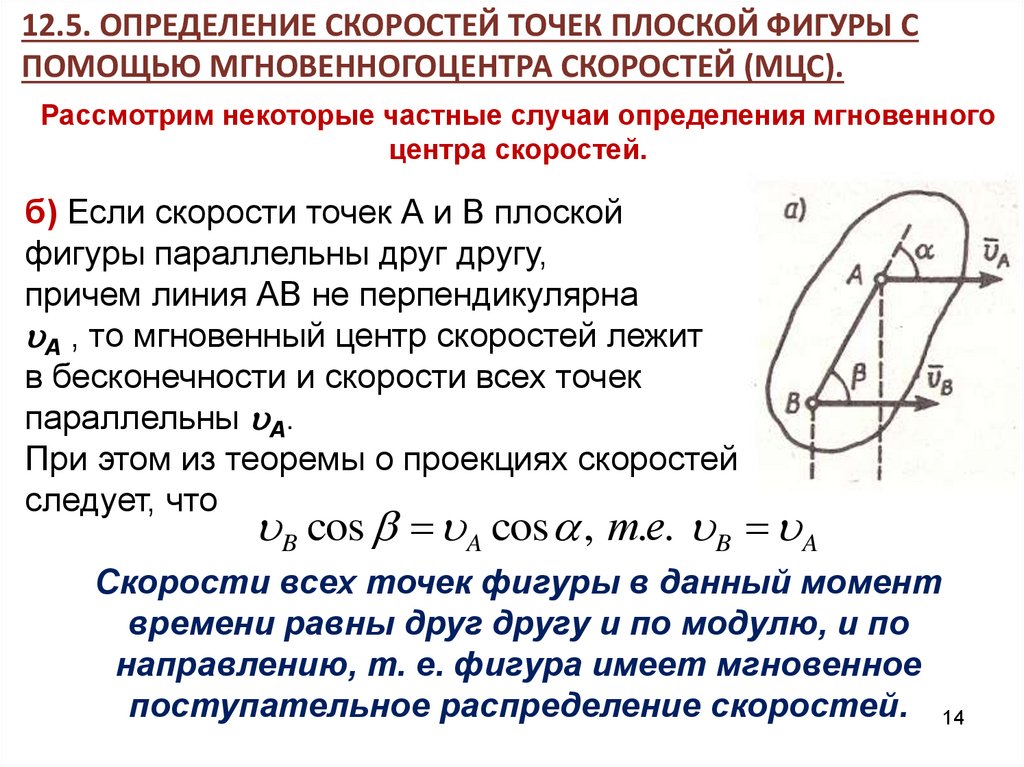
б) Если скорости точек А и В плоской
фигуры параллельны друг другу,
причем линия АВ не перпендикулярна
A , то мгновенный центр скоростей лежит
в бесконечности и скорости всех точек
параллельны A.
При этом из теоремы о проекциях скоростей
следует, что
B cos A cos , т.е. B A
Скорости всех точек фигуры в данный момент
времени равны друг другу и по модулю, и по
направлению, т. е. фигура имеет мгновенное
поступательное распределение скоростей. 14

15.

12.5. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С
ПОМОЩЬЮ МГНОВЕННОГОЦЕНТРА СКОРОСТЕЙ (МЦС).
Рассмотрим некоторые частные случаи определения мгновенного
центра скоростей.
б) Если скорости точек А и В плоской фигуры параллельны Друг другу и
при этом линия АВ перпендикулярна A, то мгновенный центр скоростей
Р определяется построением, показанным на рисунке ниже.
В этом случае, в отличие от
предыдущих, для нахождения
центра P надо кроме направлений
знать еще и модули скоростей
A и В .
г) Если известны непр-е вектора ск-ти В
какой-нибудь точки В и ее угловая
скорость , то положение мгновенного
центра скоростей Р, лежащего на
перпендикуляре к В, можно найти из
соотношения
15
B ВР

16.

12.6. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ.
Покажем, что ускорение любой точки М плоской фигуры
складывается из ускорений, которые точка получает при
поступательном и вращательном движениях этой фигуры.
Положение точки М по отношению к осям Оху определяется
радиусом-вектором r rA r '
rA - радиус-вектор полюса;
r ' AM - вектор, определяющий положение точки М.
Тогда
d 2 r d 2 rA d 2 r '
aM 2 2 2
dt
dt
dt
в этой формуле:
d 2 rA
aА 2
dt
- это ускорение полюса А.
d 2 r ' - ускорение, которое точка М получает при
aM / A 2
dt вращении фигуры вокруг полюса А.

17.

12.6. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ.
Ускорение любой точки М плоской фигуры
геометрически складывается из ускорения какойнибудь другой точки А , принятой за полюс, и
ускорения, которое точка М получает при вращении
фигуры вокруг этого полюса.
aM aA aM / A .
Значение аМ/А, как ускорения точки
вращающегося твердого тела,
определяется по формуле:
aM / A MA 2 4 , tg / 2 .
Модуль и направление ускорения ам находятся
построением соответствующего параллелограмма,
представленного на рисунке справа.
17

18.

12.6. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ.
Однако вычисление аА с помощью параллелограмма,
изображенного на рисунке на предыдущем слайде,
достаточно трудоёмко, так как необходимо находить
значение угла , а затем — угла между векторами аМ/А и аА.
При решении задач удобнее вектор аМ/А заменять его
n
касательной a MA нормальной a MA
составляющими:
n
aM a A aMA
aMA
.
- вектор a MA
направлен перпендикулярно
АМ в сторону вращения, если оно
ускоренное, и против вращения, если
оно замедленное;
n
- вектор a MA всегда направлен от точки
М к полюсу А.
n
a MA AM , aMA
AM 2 .
18

19. Цент О колеса, катящегося по прямолинейному рельсу, имеет в данный момент времени скорость 0=1 м/с и ускорение а0=2 м/с2.

12.6. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ.
Цент О колеса, катящегося по прямолинейному рельсу, имеет в данный
момент времени скорость 0=1 м/с и ускорение а0=2 м/с2. Радиус колеса
R=0,2 м. определить ускорение точки Р, совпадающей с мгновенным
центром скоростей.
Решение:
1) Так как v0 и а0 известны, принимаем
точку О за полюс.
2) Определим угловую скорость .
Точка касания Р является, мгновенным
центром скоростей, следовательно,
угловая скорость колеса
0
РО
0
R
.
3) Определим угловое ускорение . Так как величина PO = R остается
постоянной при любом положении колеса, то, дифференцируя это равенство
по времени, получим
d 1 d 0 a0
.
dt R dt
R
Знаки и совпадают, следовательно, вращение колеса ускоренное.
19

20.

12.6. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ.
Решение:
a
4) Определим касательную ВО и
n
осестремительную a ВО
составляющие
ускорения точки В при вращении вокруг
полюса О:
n
aB a0 aBO aBO .
Зная, что ВО = R, найдём
n
a BO BO a0 2 м/с2 , aBO
BO 2 02 / R 5м/с2 .
5) По теореме об ускорении точек плоской фигуры, найдём ускорение точки В:
n
aBx aBO
a0 3м/с 2 , aBy a BO 2 м/с 2 ,
2
2
aB aBx
aBy
13 3, 6 м/с 2 .

21.

12.7. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ.
При непоступательном движении плоской
фигуры у нее в каждый момент времени имеется
точка Q, ускорение которой равно нулю.
Эта точка называется
мгновенным центром ускорений.
Положение мгновенного центра ускорений Q
определяется следующим образом:
1) находим значение угла из формулы
tg / 2 .
2) от точки А под углом к вектору a А
проводим прямую АЕ.
Прямая АЕ должна быть отклонена от a А
в направления углового ускорения , т.е. в сторону
вращения фигуры, если вращение является ускоренным, и против
вращения, если оно является замедленным.
3) откладываем вдоль линии АЕ отрезок AQ, равный AQ a A /
2 4 .

22.

12.7. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ.
Построенная таким путем точка Q и будет
мгновенным центром ускорений.
aQ aA aQA , где aQA AQ 2 4 .
2
4
AQ
a
/
, вычисляем
Учитывая, что
A
что a A aQA .
Эти вектора параллельны друг другу, но
направлены в противоположную сторону, поэтому
aQA a A и aQ 0.
Если точку Q выбрать за полюс, то так как aQ 0 , ускорение любой
точки М тела будет
aМ aQ aM /Q aM /Q , aM MQ 2 4 .
Ускорения точек плоской фигуры определяются в
данный момент времени так, как если бы движение
фигуры было вращением вокруг мгновенного центра
ускорений Q.

23.

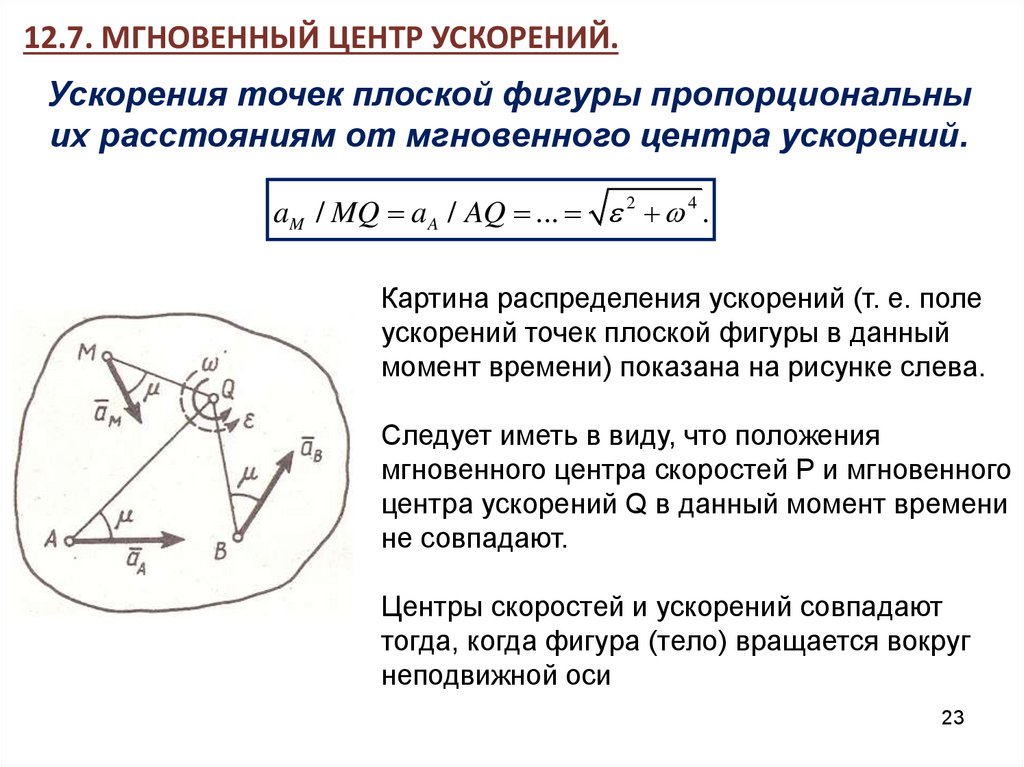
12.7. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ.
Ускорения точек плоской фигуры пропорциональны
их расстояниям от мгновенного центра ускорений.
aM / MQ a A / AQ ... 2 4 .
Картина распределения ускорений (т. е. поле
ускорений точек плоской фигуры в данный
момент времени) показана на рисунке слева.
Следует иметь в виду, что положения
мгновенного центра скоростей Р и мгновенного
центра ускорений Q в данный момент времени
не совпадают.
Центры скоростей и ускорений совпадают
тогда, когда фигура (тело) вращается вокруг
неподвижной оси
23

24.

12.7. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ.
Колесо катится по прямолинейному рельсу так, что
скорость его центра постоянна. Определить ускорение
точки М обода колеса.
Решение:
По условиям задачи С const , aC 0.
Следовательно, точка С является мгновенным центром ускорений.
Мгновенный центр скоростей находится в точке Р.
Для колеса угловая скорость и угловое ускорение:
С / PC С / R const ,
d / dt 0, tg / 2 0, 0.
Таким образом, ускорение любой точки М обода
(в том числе и точки Р) направлено к центру С
Колеса и равно
aM MC 2 C2 / R.
aMn aM cos , a M aM sin .
24

25. Кривошип ОА вращается с постоянной угловой скоростью ОА. Найти ускорение ползуна В и угловое ускорение шатуна АВ в тот момент

12.7. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ.
Кривошип ОА вращается с постоянной угловой скоростью ОА. Найти
ускорение ползуна В и угловое ускорение шатуна АВ в тот момент
времени, когда ВОА=90 , если ОА=r, AB=l.
МЦС стремится к нулю.
Решение:
В рассматриваемый момент времени скорости всех точек шатуна АВ равны
А.
Мгновенный центр скоростей находится в бесконечности и АВ = 0. Тогда
2
АВ 0. tg AB / AB
и 90
Ускорение точки А направлено вдоль АО. Ускорение точки В, так как она
движется прямолинейно, направлено вдоль ОВ.
В данном случае = 90°. Линии АQ и BQ должны быть перпендикулярны
аА и аВ. Восставляя эти перпендикуляры,
находим, положение точки Q.
Тогда
aB / BQ a A / AQ,
где BQ r , AQ l 2 r 2 .

26.

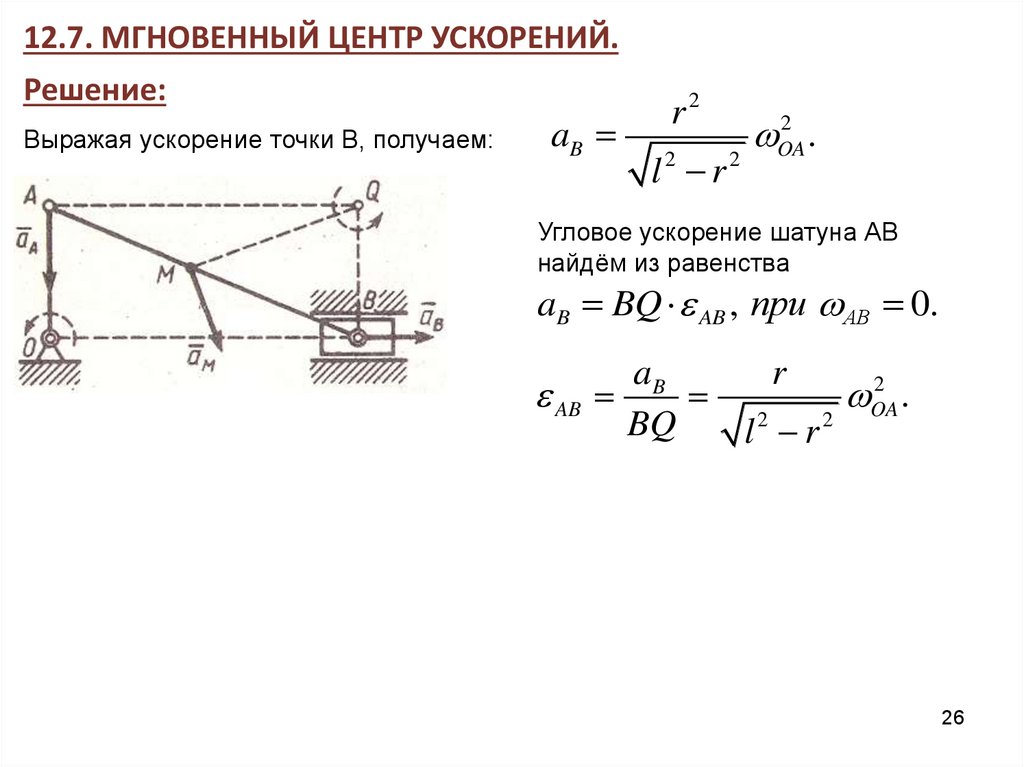
12.7. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ.
Решение:
Выражая ускорение точки В, получаем:
aB
r2
l2 r2
2
OA
.
Угловое ускорение шатуна АВ
найдём из равенства
aB BQ AB , при АВ 0.
aB
r
2
AB
OA
.
2
2
BQ
l r
26

27.

Любишь
компьютеры?
Обожаешь
проводить время в
сети Интернет?
О, мы понимаем тебя,
в сети много интересного!
Но!!! Ты знаешь, что кроме
приятного,
в Интернете еще и великое
множество подстерегающих
опасностей
Хочешь избежать проблем и чувствовать
себя в сети свободно и защищённо?
Конечно, да!!! Тогда знай, мы уже
позаботились о тебе!
Просто пройди по QR
коду и узнай основные
правила
кибербезопасности!!!