Плоскопараллельное движение тела

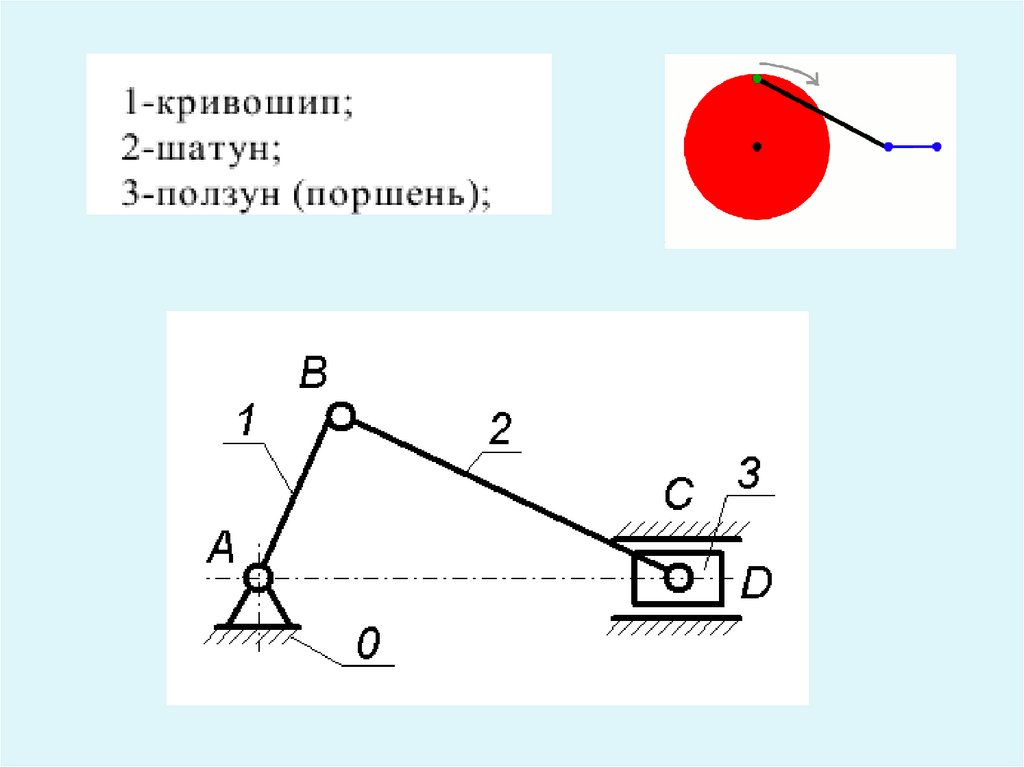
1.

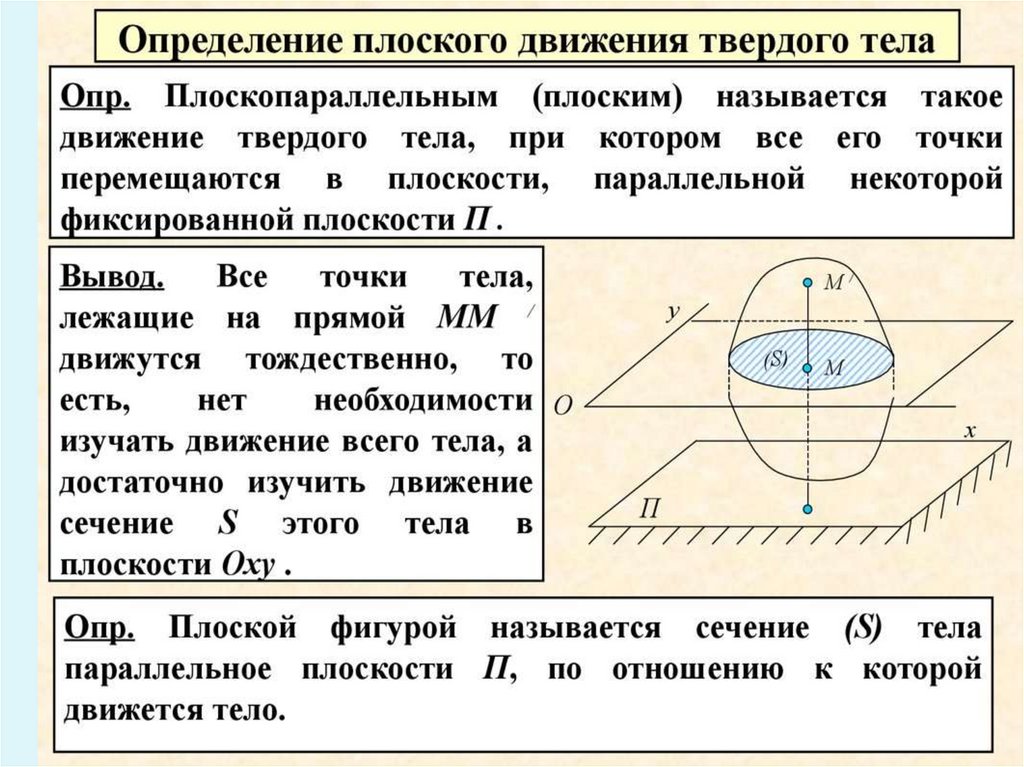
3.3. Плоскопараллельное движение тела
Плоскопараллельным (плоским) называется такое
движение тела, при котором все его точки описывают
траектории, параллельные некоторой неподвижной
плоскости

2.

3.

4.

5.

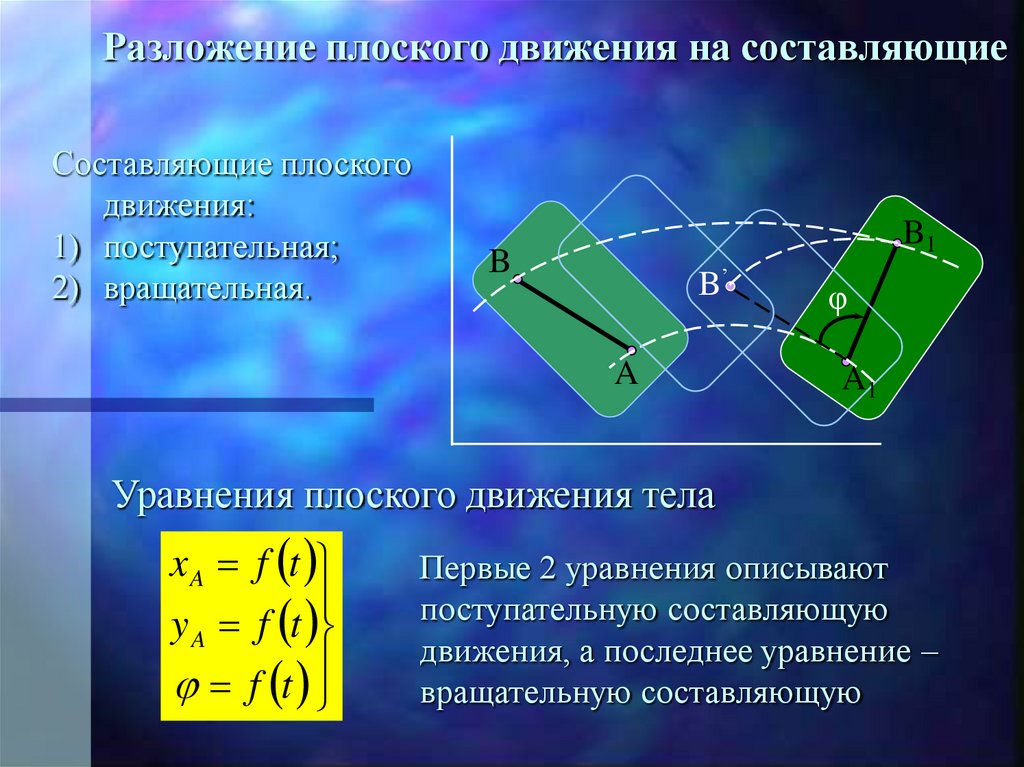
Разложение плоского движения на составляющие
Составляющие плоского
движения:
1) поступательная;
2) вращательная.
B1
B
B’
A
φ
A1
Уравнения плоского движения тела
x A f t
y A f t
f t
Первые 2 уравнения описывают
поступательную составляющую
движения, а последнее уравнение –
вращательную составляющую

6.

7.

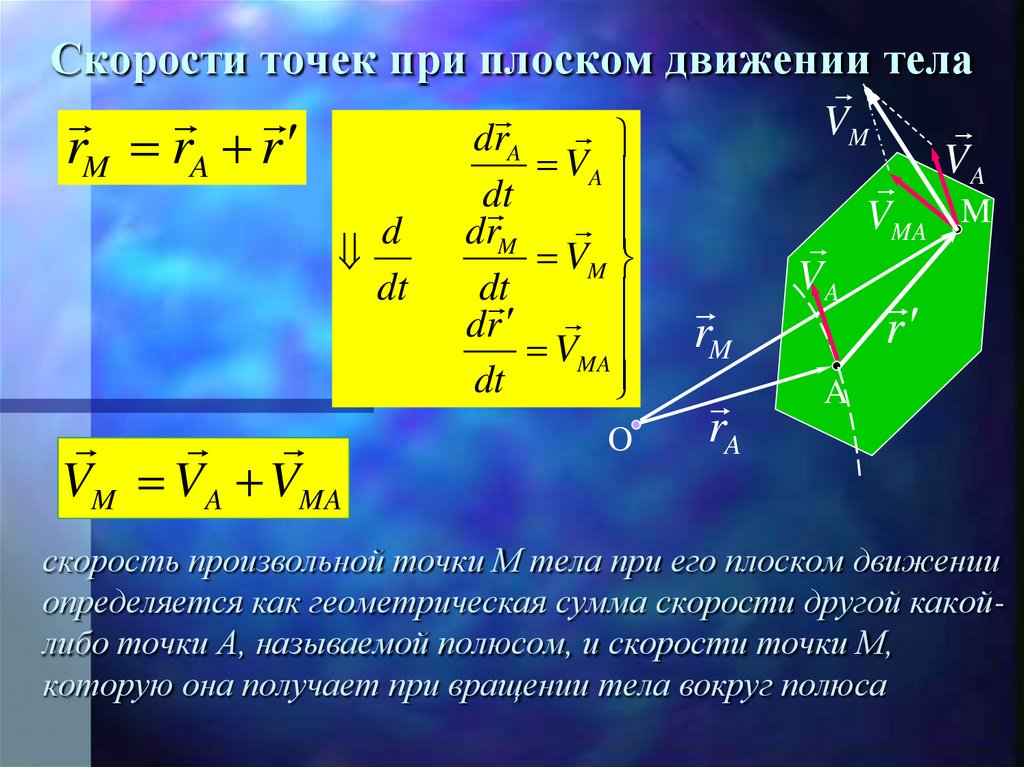
Скорости точек при плоском движении тела
rM rA r
d
dt
VM VA VMA
drA
VA
dt
drM
VM
dt
dr
VMA
dt
O
VM
rM
rA
VA
VA
VMA M
r
A
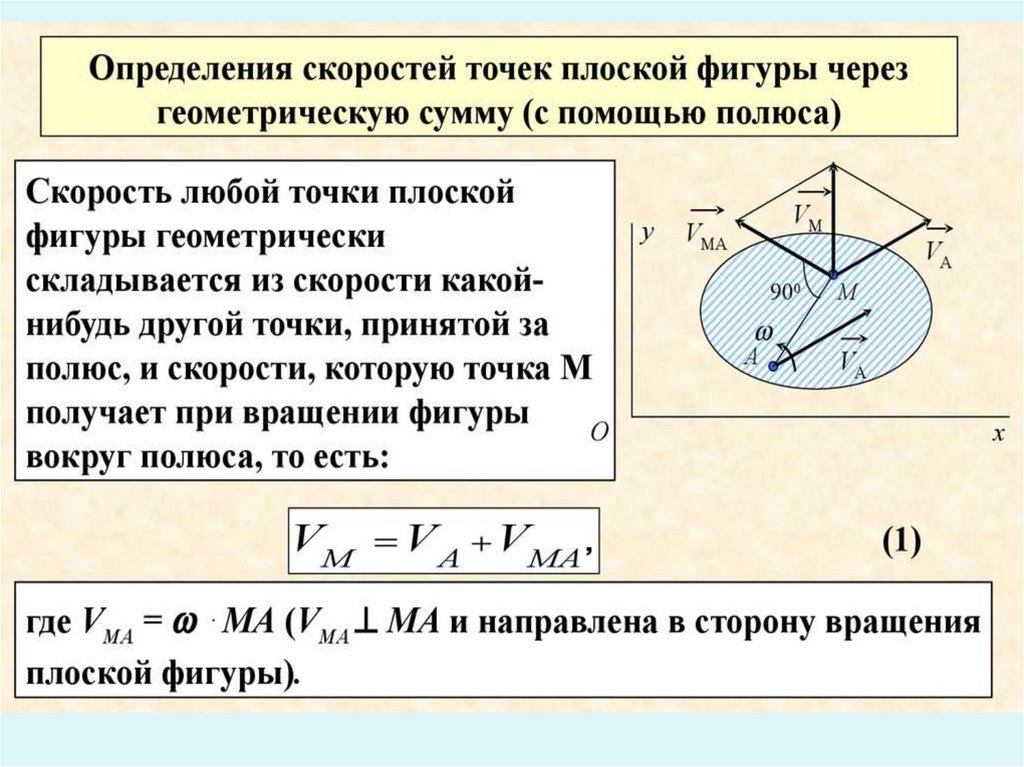
скорость произвольной точки М тела при его плоском движении
определяется как геометрическая сумма скорости другой какойлибо точки А, называемой полюсом, и скорости точки М,
которую она получает при вращении тела вокруг полюса

8.

9.

Теорема о проекциях скоростей 2-х точек
проекции скоростей двух точек тела, совершающего
плоское движение, на прямую, проходящую через эти
точки, равны между собой
VB V A VBA
VB V
A
VBx VAx VBAx
VBx VB cos
VA
VBA
x
B
A
VAx VA cos
VB cos VA cos
VBAx VBA cos 90 0

10.

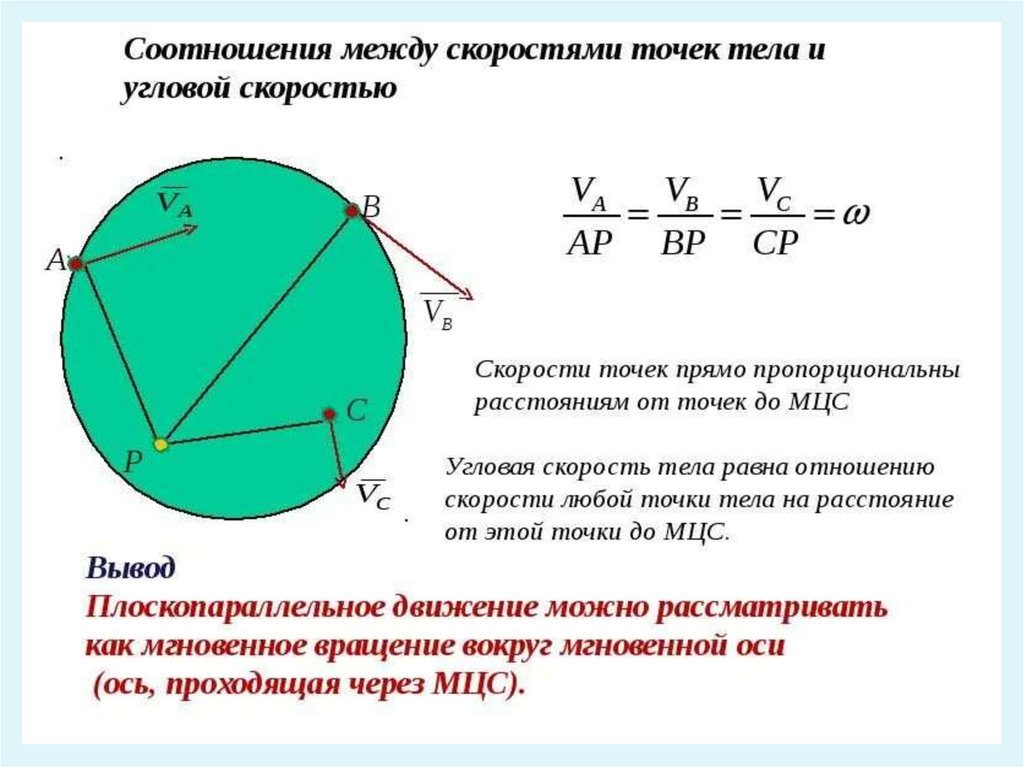
Мгновенный центр скоростей (МЦС)
Мгновенным центром скоростей (или мгновенным
центром вращения) называют ту точку плоской фигуры,
скорость которой в данный момент времени равна нулю.
Далее мы будем обозначать мгновенный центр скоростей буквой P. Для
плоской фигуры – это точка. Для твердого тела – это ось, проходящая через
точку P перпендикулярно плоскости движения.
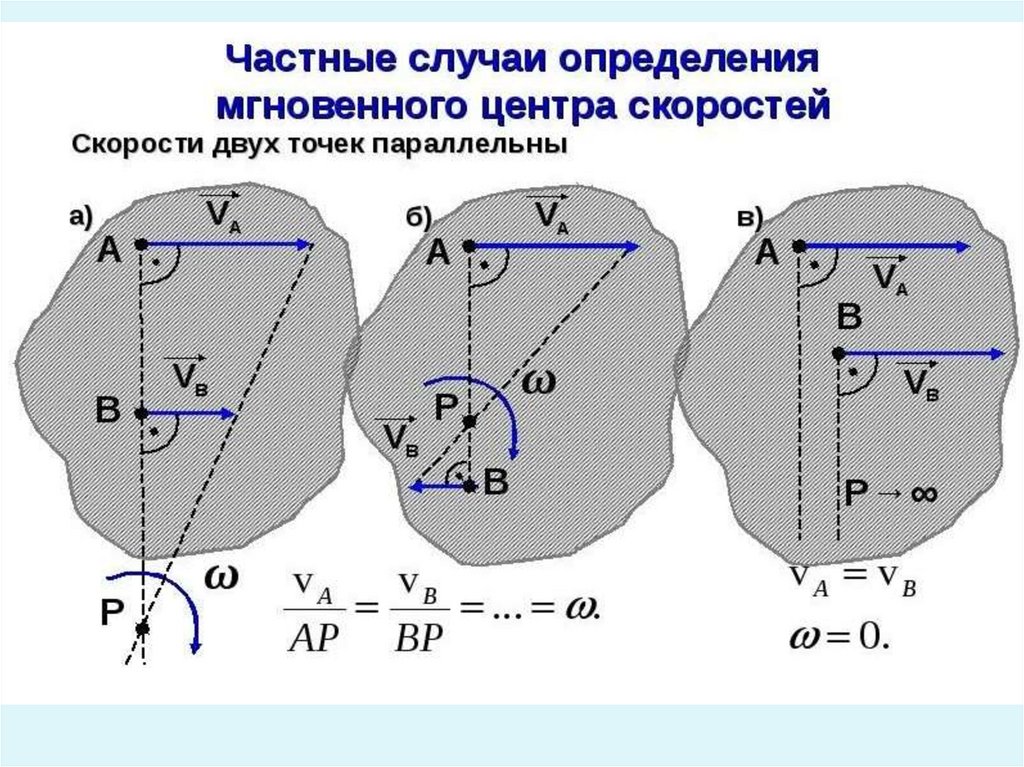
Если известна скорость точки А и направление скорости точки В,
МЦС находится на пересечении перпендикуляров к скоростям,
проведённых в точках А и В .

11.

12.

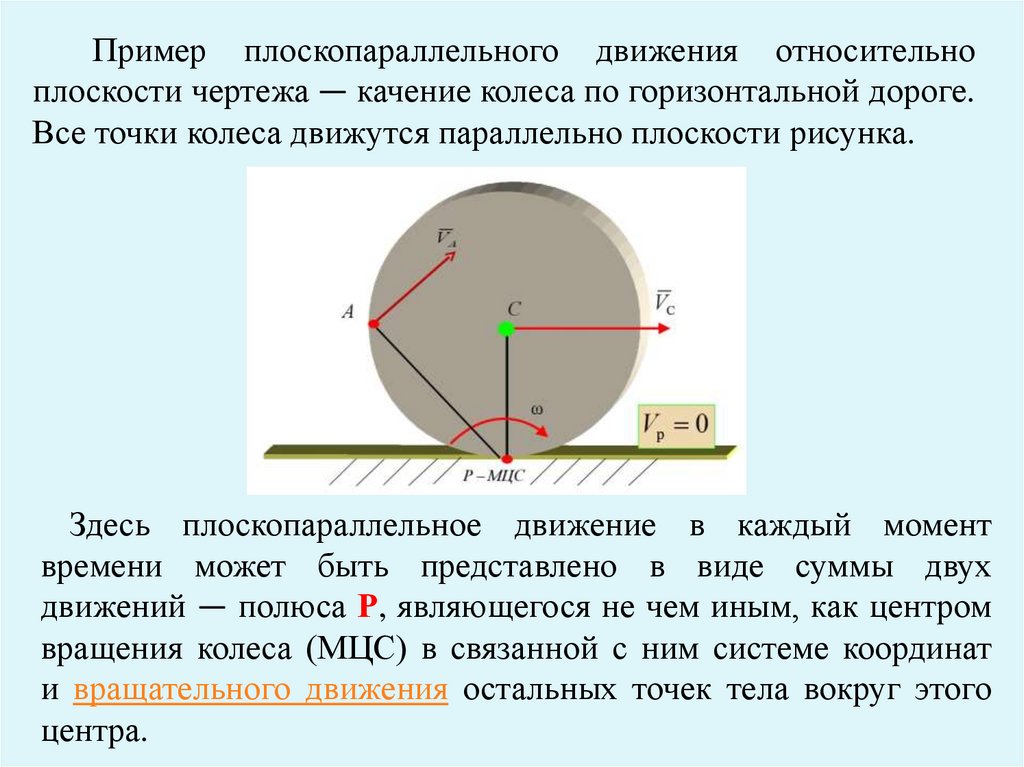
Пример плоскопараллельного движения относительно
плоскости чертежа — качение колеса по горизонтальной дороге.
Все точки колеса движутся параллельно плоскости рисунка.
Здесь плоскопараллельное движение в каждый момент
времени может быть представлено в виде суммы двух
движений — полюса Р, являющегося не чем иным, как центром
вращения колеса (МЦС) в связанной с ним системе координат
и вращательного движения остальных точек тела вокруг этого
центра.

13.

ВЫВОДЫ:
1) практическое значение МЦС заключается в
том, что с его помощью геометрически
сложное плоское движение тела можно
рассматривать как простое мгновенно
вращательное движение относительно оси,
проходящей через МЦС;
2) скорость произвольной точки тела,
совершающего плоское движение,
определяется как скорость, которую она
получает при вращении тела вокруг МЦС

14.

15.

Ускорение любой точки М тела геометрически складывается
из ускорения какой-либо другой точки, принятой за полюс, и
ускорения точки М в ее вращении вместе с телом вокруг этого
полюса.
Модуль
и
направление
ускорения aM находятся
соответствующего параллелограмма.
Вектор
построением
направлен перпендикулярно АМ в сторону вращения, если оно
ускоренное, и против вращения, если оно замедленное; вектор
направлен от точки М к полюсу А
всегда