Похожие презентации:
Загадка последовательности Фибоначчи
1.
Загадкапоследовательности
Фибоначчи
Выполнила: ученица 11 А
Дорофеева Светлана
Руководитель: учитель информатики
Старостоянова Ольга Александровна
2.
Цель:Разработать видеоролик о
проявлениях
последовательности Фибоначчи
в природе для использования на
уроках естественноматематического цикла
3.
ЗадачиПроследить этапы исторического
возникновения последовательности
Фибоначчи
Описать геометрический смысл
последовательности Фибоначчи
✔
Исследовать применение числа ФИ в
различных областях исскуства и природе
✔
Исследовать множество программного
обеспечения для монтажа видео
✔
Подобрать материал для видеоролика
✔
4.
Итальянский математикЛеонардо Фибоначчи
любил гулять по лесу и
размышлять. Например, о
том, с какой прогрессией
рождаются кролики.
Неизвестно, долго ли он над
этим думал, но именно
размышляя о кроликах,
придумал числовой ряд,
каждое последующее число
которого являлось суммой
двух предыдущих: 1, 1, 2, 3, 5,
8, 13, 21, 34, 55, 89, 144, 233, 377,
610, 987, 1597 и так до
бесконечности. Стоило
Фибоначчи вывести эту
закономерность, как они
5.
Числа Фибоначчи в природеУ небольших соцветий подсолнуха
спирали по 34 и 55 семян, а у
крупных соцветий по 55 и 89. Это
происходит благодаря тому, что они
выложены
в
виде
двух
пересекающихся спиралей. Справа
налево и наоборот. Эти комбинации
не случайно совпадают с числами
Фибоначчи.
6.
Числа Фибоначчи в природеКоличество лепестков
во многих соцветиях
совпадает с числами из
этой
последовательности.
Ветви и листья деревьев
расположены в таком
порядке, чтобы получать
максимум света,
поэтому они
распределены в
последовательности
основанной на
последовательности
Фибоначчи. Благодаря
этому они не мешают
7.
Загадочное число ФиЭта
последовательность
обладает
потрясающими
свойствами. Одно из
которых состоит в том,
что
при
делении
каждого
последующего
числа
на
предыдущее
в
результате получается
бесконечная
десятичная
дробь,
которая мистическим
образом приближается
к числу фи.
8.
Геометрический смыслпоследовательности
Фибоначчи
Одно
из
замечательных
свойств
последовательности Фибоначчи - логарифмическая
спираль, которая разворачивается, используя
золотое число, как геометрический индекс.
9.
Золотое число в природеЧисло
Фи
можно
встретить наблюдая
за
ростом рогов
некоторых
жвачных
животных.
В паутине пауков тоже
видна
золотая
пропорция.
10.
Божественная пропорция ичеловек
Отношение длины предплечья и длины ладони
тоже дает вездесущую божественную пропорцию.
11.
Золотое число в природеСпиральные галактики
12.
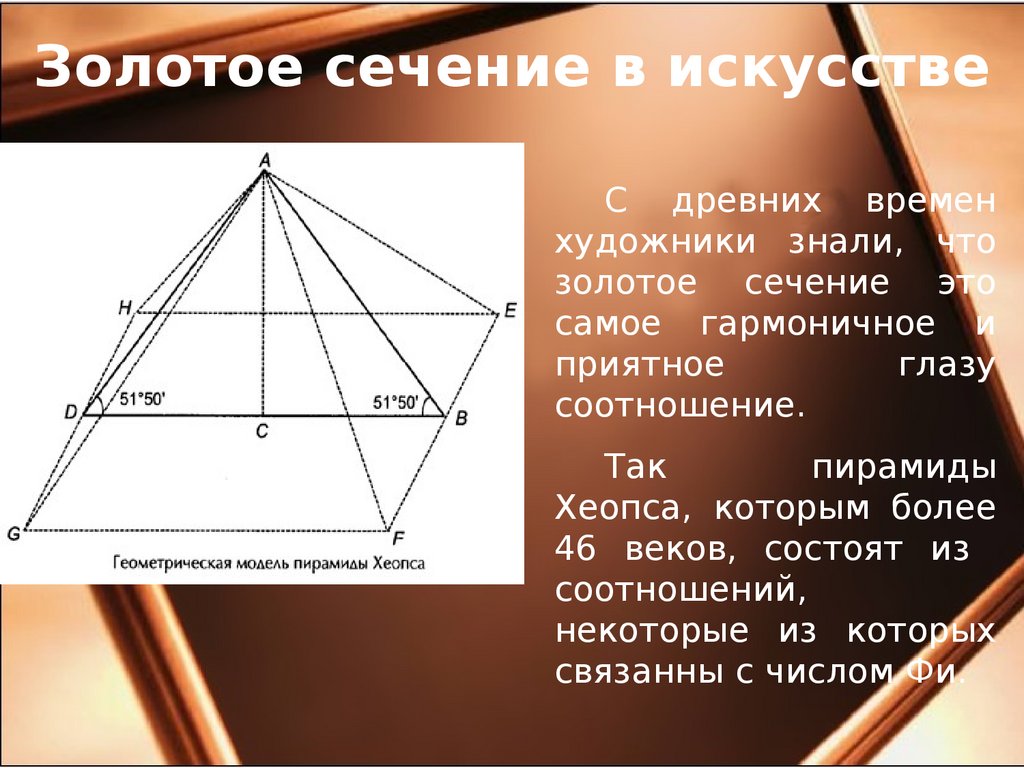
Золотое сечение в искусствеС древних времен
художники знали, что
золотое сечение это
самое гармоничное и
приятное
глазу
соотношение.
Так
пирамиды
Хеопса, которым более
46 веков, состоят из
соотношений,
некоторые из которых
связанны с числом Фи.
13.
Золотое сечение вискусстве
Термин «Золотое
сечение ввел
Леонардо да
Винчи». Его
произведение
«Витрувианский
человек»
является
неявным
символом
внутренней
симметрии
14.
ПоследовательностьФибоначчи в современности
15.
1.2.
3.
4.
5.
6.
7.
8.
Источники информации:
Ковалев Ф.В. Золотое сечение в живописи. К.:
школа, 1989.
Кеплер И. О шестиугольных снежинках. – М.,
1982.
Дюрер А. Дневники, письма, трактаты – Л., М.,
1957.
Шубников А. В., Копцик В. А. Симметрия в науке
и искусстве. -М.: Наука, 1972.
Пидоу Д.. Геометрия и искусство. – М.: Мир,
1989.
Воробьев Н.Н. Числа Фибоначчи.-М., 1984.
Энзензбергер
Ханс
Магнус
Дух
числа.
Математические приключения. – Пер. с англ. –
Харьков: Книжный Клуб "Клуб Семейного
Досуга", 2004. – 272 с.
Энциклопедия символов /сост. В.М. Рошаль. –
Москва: АСТ; СПб.; Сова, 2006. – 1007 с.














 Математика
Математика