Геометрические построения

1. Геометрические построения

1. Окружность
2. Окружность, описанная около
треугольника.
3. Касательная к окружности.
4. Окружность, вписанная в треугольник.
5. Задачи на построение
6. Геометрическое место точек.

2.

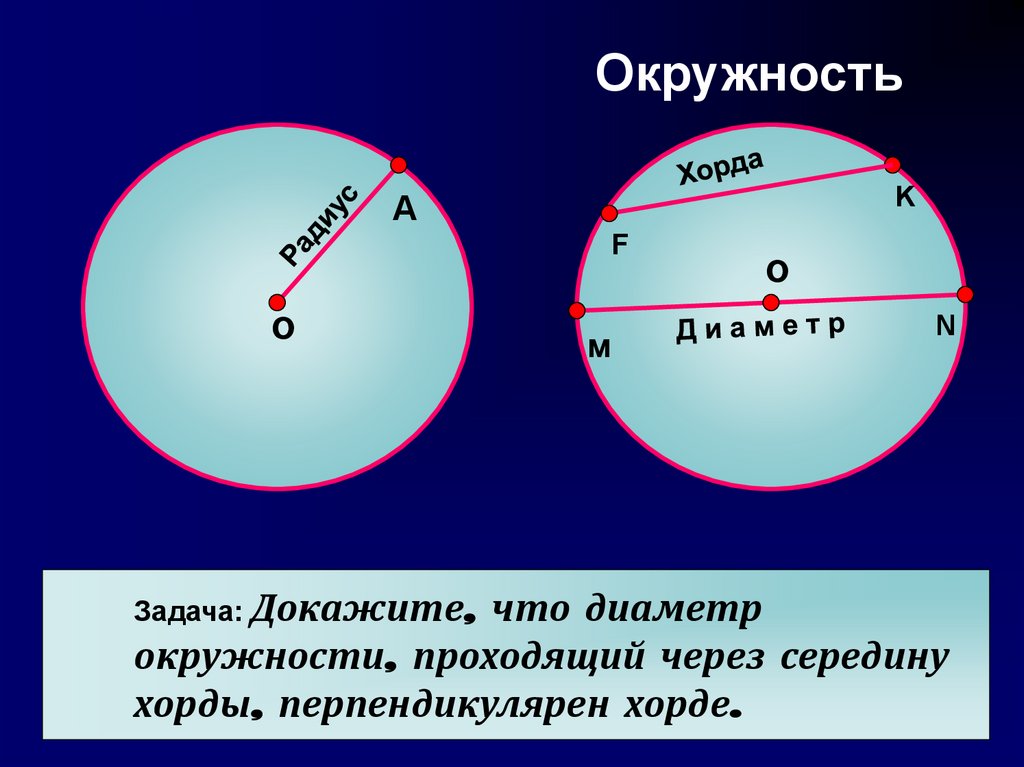
Окружность
K
А
F
о
Задача: Докажите,
м
о
N
что диаметр
окружности, проходящий через середину
хорды, перпендикулярен хорде.

3.

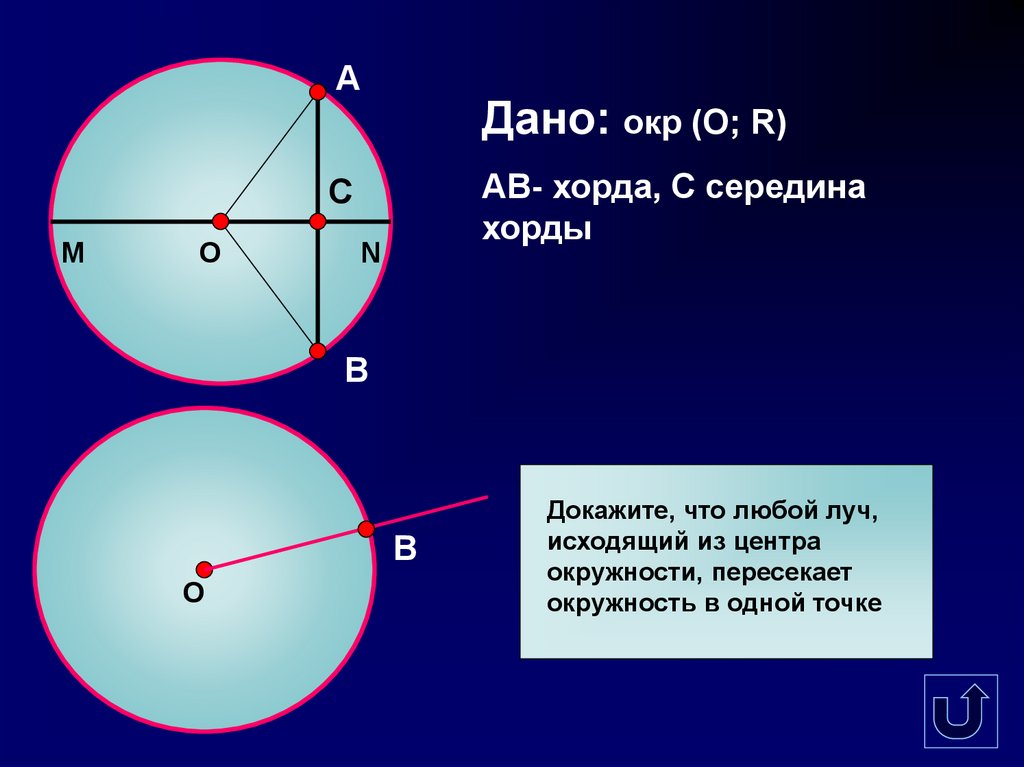
А
Дано: окр (О; R)
АВ- хорда, С середина
хорды
С
M
О
N
В
В
О
Докажите, что любой луч,
исходящий из центра
окружности, пересекает
окружность в одной точке

4.

А
О
В
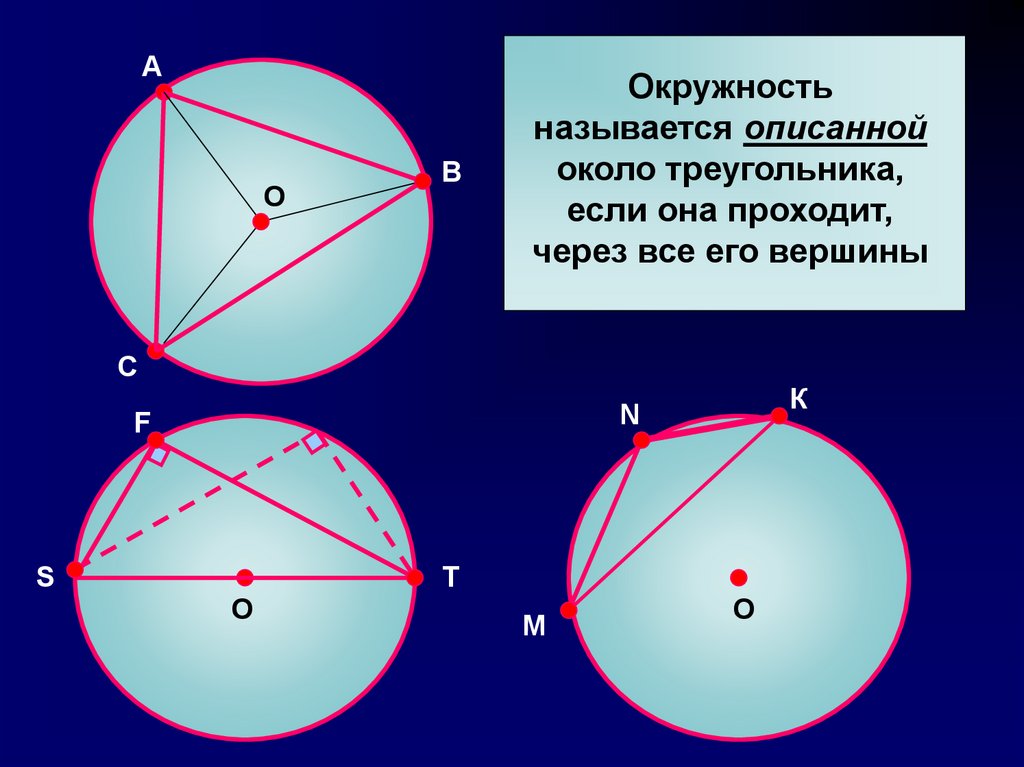
Окружность
называется описанной
около треугольника,
если она проходит,
через все его вершины
С
К
N
F
S
T
О
М
О

5.

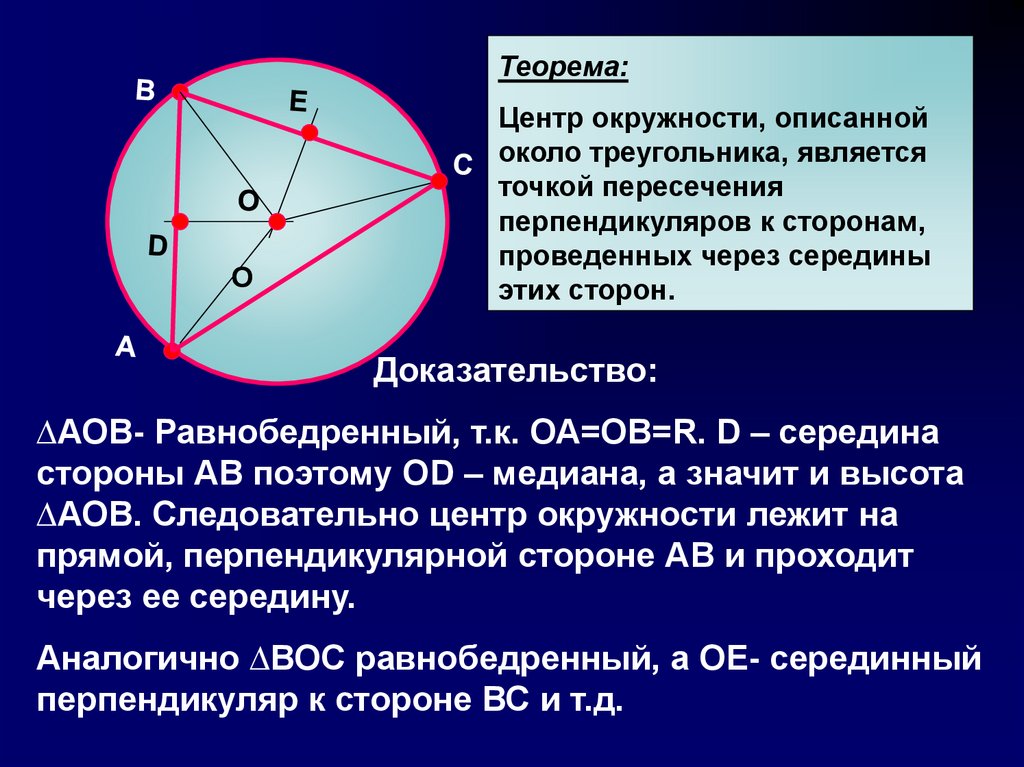
Теорема:
О
Центр окружности, описанной
около треугольника, является
точкой пересечения
перпендикуляров к сторонам,
проведенных через середины
этих сторон.
Доказательство:
∆АОВ- Равнобедренный, т.к. ОА=ОВ=R. D – середина
стороны АВ поэтому ОD – медиана, а значит и высота
∆АОВ. Следовательно центр окружности лежит на
прямой, перпендикулярной стороне АВ и проходит
через ее середину.
Аналогично ∆ВОС равнобедренный, а ОЕ- серединный
перпендикуляр к стороне ВС и т.д.

6.

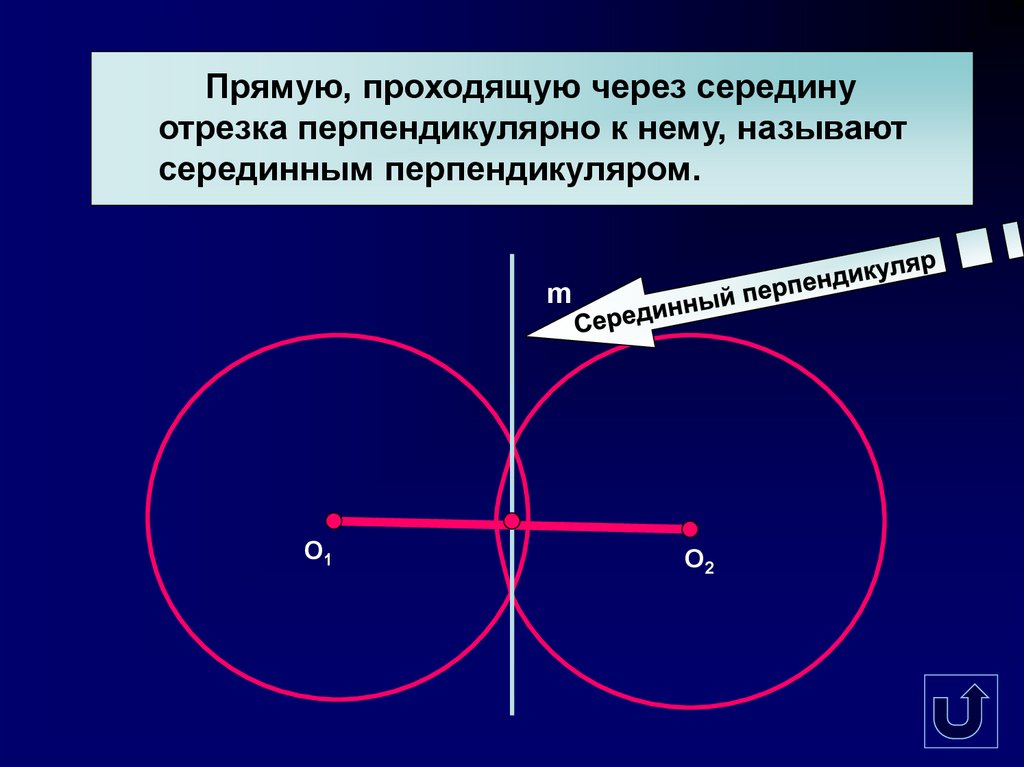
Прямую, проходящую через середину
отрезка перпендикулярно к нему, называют
серединным перпендикуляром.
m
О1
О2

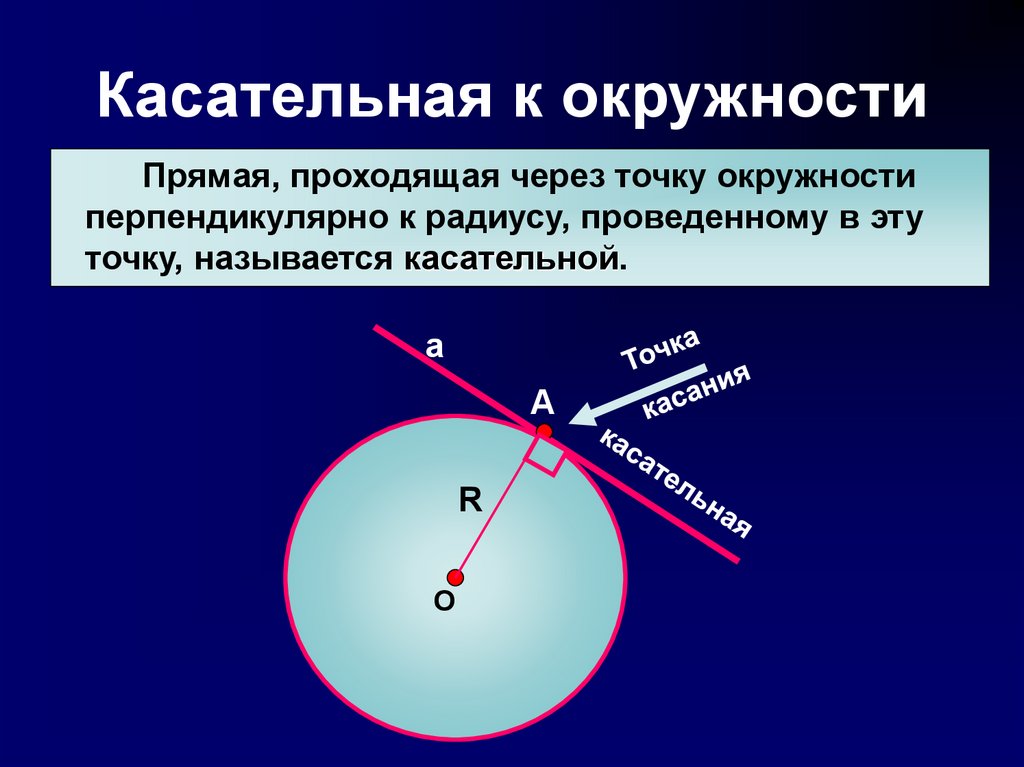
7. Касательная к окружности

Прямая, проходящая через точку окружности
перпендикулярно к радиусу, проведенному в эту
точку, называется касательной.
a
А
R
О

8.

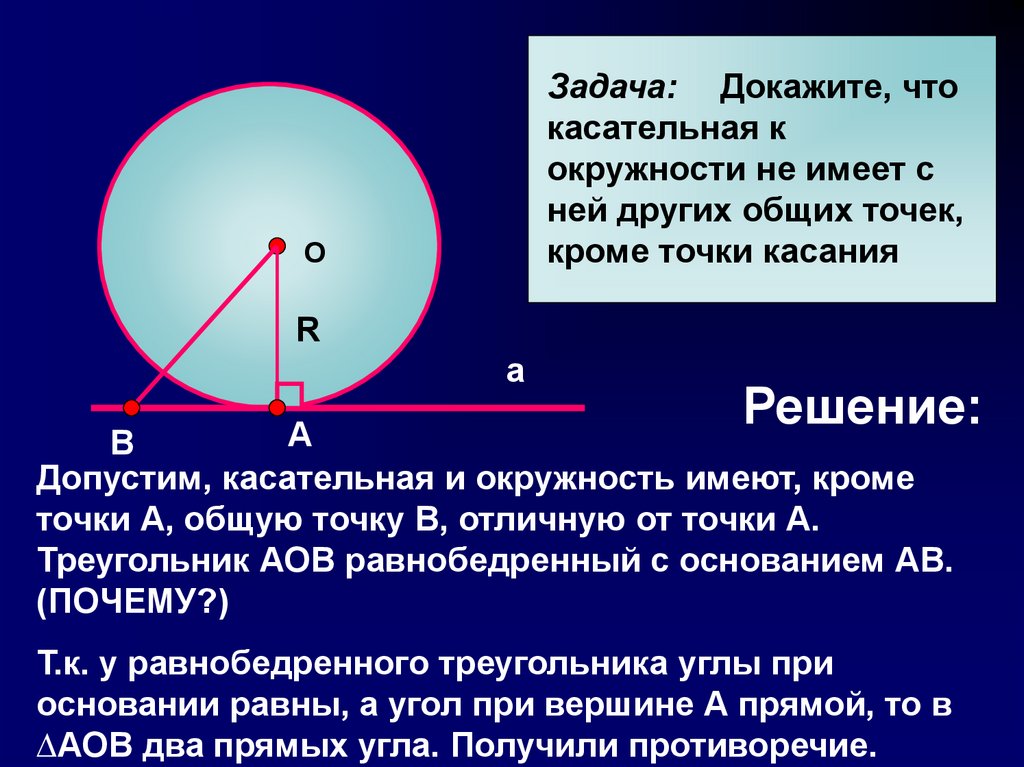
Задача: Докажите, что
касательная к
окружности не имеет с
ней других общих точек,
кроме точки касания
О
R
a
Решение:
А
В
Допустим, касательная и окружность имеют, кроме
точки А, общую точку В, отличную от точки А.
Треугольник АОВ равнобедренный с основанием АВ.
(ПОЧЕМУ?)
Т.к. у равнобедренного треугольника углы при
основании равны, а угол при вершине А прямой, то в
∆АОВ два прямых угла. Получили противоречие.

9.

Теорема:Окружность
Центрназывается
окружности,
вписанной в треугольник, если
вписанной
в треугольник,
является
она касается
всех его сторон
точкой пересечения его биссектрис.
С
Доказательство:
Е
F
O
D
A
Пусть АВС-данный треугольник, О-центр
вписанной в него окружности, D,E и F- точки
касания окружности со сторонами.
BПрямоугольные треугольники АОD и АОЕ равны
по гипотенузе и катету. У них гипотенуза АО
общая, а катеты ОD и ОЕ равны как радиусы. Из
равенства треугольников следует равенство
углов ОАD и ОАЕ. А это значит, что точка О лежит на
биссектрисе треугольника, проведенной из вершины
А. Точно так же доказывается, что точка О лежит на
двух других биссектрисах треугольника

10. Задачи на построение

1) Построение треугольника с
данными сторонами
2) Построение треугольника равного
данному
3) Построение биссектрисы угла
4) Деление отрезка пополам
5) Построение перпендикулярной
прямой

11.

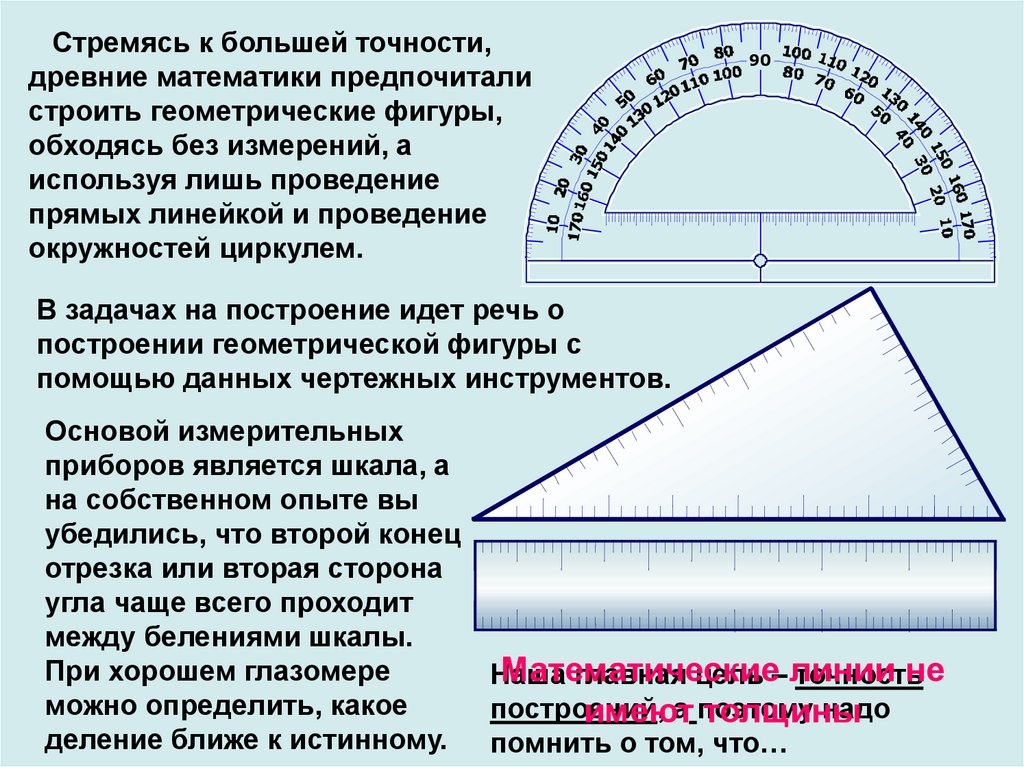
Стремясь к большей точности,
древние математики предпочитали
строить геометрические фигуры,
обходясь без измерений, а
используя лишь проведение
прямых линейкой и проведение
окружностей циркулем.
90
В задачах на построение идет речь о
построении геометрической фигуры с
помощью данных чертежных инструментов.
Основой измерительных
приборов является шкала, а
на собственном опыте вы
убедились, что второй конец
отрезка или вторая сторона
угла чаще всего проходит
между белениями шкалы.
При хорошем глазомере
можно определить, какое
деление ближе к истинному.
Математические
не
Наша
главная цель – линии
точность
построений,
а поэтому
надо
имеют
толщины
помнить о том, что…