Технологические процессы автоматизированных производств (ТПАП)

1.

Технологические процессы
автоматизированных производств
(ТПАП)
Лекционный курс
Часть 2

2.

Анализ типового ТП как объекта управления
Емкостной смеситель
1 этап. Разработка концептуальной модели
Краткая характеристика объекта
В аппарат емкостного типа с интенсивно
работающей мешалкой подаются две жидкости,
расходы, концентрации полезного компонента и
температуры которых равны соответственно υ1,
c1, t1 и υ2, c2, t2. Выходящий поток жидкости
имеет состав с, температуру t. Расход
выходящего потока определяется расходной
характеристикой насоса.
Назначение ХТП: смешение двух потоков жидкости, с различными концентрациями
полезного компонента и различными температурами.
Цель функционирования:
1) получить поток с необходимым – заданным значением концентрации
компонента – Сз;
2) получить поток с необходимым заданным значением температуры раствора ( tз).
2

3.

Классификация технологических параметров
Переменные состояния:
Уровень жидкости в смесителе h характеризует общее количество вещества в аппарате.
Ограничение может быть наложено на максимальное и минимальное значения уровня
жидкости в аппарате.
Концентрация полезного компонента С–характеризует количество компонента в
аппарате и отражает назначение и цель его функционирования.
Температура t – характеризует количество тепловой энергии внутри аппарата.
Входные переменные:
υ1, c1, t1, υ2, c2, t2, - расходы, концентрации, температуры входных потоков и расход
жидкости на выходе. Характеризуют внешние воздействия на состояние объекта и
часть из них может целенаправленно меняться (оказывать регулирующее воздействие).
Критерий эффективности
В соответствии с целью функционирования объекта эффективность его работы
можно оценить по степени достижения цели, т.е.:
1) близости концентрации к заданной величин , в качестве критерия эффективности
можно использовать величину R (C Cз ) 2 min
2) близости температуры t к заданной величине tз , качестве критерия эффективности
предлагается использовать величину R (t t з ) 2 min
3

4.

2 этап. Построение математической модели
Упрощающие допущения:
1. Принимаем модель идеального смешения ввиду высокой степени
турбулизации содержимого емкости. Параметры выходного потока совпадают
с параметрами жидкости внутри аппарата (концентрации, температура).
2. Теплофизические свойства входных потоков, выходного потока и жидкости
внутри аппарата совпадают и не зависят от температуры и концентрации
( , , cp =const).
3. Потери вещества и энергии во внешнюю среду отсутствуют.
В соответствие с законами сохранения вещества и энергии уравнения
материального и теплового баланса примут вид:
d V
1 2
d
d V С
1С1 2 С 2 С
d
d cp V t
d
материальный баланс по жидкой фазе в целом;
материальный баланс по полезному компоненту;
c t c t c t
p 11
p 2 2
p
тепловой баланс емкости
4

5.

Выполним преобразования:
dV
1 2 ,
d
d V С
d
1С1 2 С 2 С ,
(1)
d V t
1t1 2 t 2 t.
d
Начальные условия: V 0 V 0 , C 0 C0 , t 0 t 0 , где V0, C0 , t 0 – решение уравнений статики
Система уравнений (1) описывает условия динамики.
Уравнения статики
0 10 02 0 ,
0 10 С10 02 С02 0 С0 ,
(2)
0 10 t10 02 t 02 0 t 0 .
5

6.

d V C
dC
dV
,
V
C
d
d
d
d V t
dt
dV
.
V t
d
d
d
Подставив эти соотношения в уравнения модели (1) получим:
dV
1 2 ,
d
dC
dV
dC
V
C
V
C 1 2 ,
d
d
d
dt
dV
dt
V t
V t 1 2 .
d
d
d
Система примет вид:
dV
1 2 ,
d
dC
V
1C1 2C2 1C 2C ,
d
dt
V
1t1 2 t 2 1t 2 t .
d
(3)
6

7.

3 ЭТАП Исследование математической модели
Для исследования объекта проведем линеаризацию уравнений
математической модели путем разложения всех функций в ряд Тейлора в
окрестности рабочей точки C i0 , t i0 , i0 , h 0 .:
Ci Ci0 Ci ; i i0 i ; t i t i0 t i ; h h 0 h;
При этом запишем первое уравнение системы (3) третьим по счету.
dC
V
1C1 2C2 1C 2C ,
d
dt
V
1t1 2 t 2 1t 2 t
d
dh
S0
1 2 .
d
7

8.

Шаг1
Подставим текущие значения переменных в уравнения модели. Выполним
алгебраические преобразования (раскроем скобки, перемножим и т.п.).
Рассмотрим на примере первого уравнения:
V
0 d (C
C)
( 10 1 ) (C10 C1 ) ( 02 2 ) (C 02 C 2 ) ( 10 1 02 2 )
d
0
(C0 C) 10 C10 10 C1 1C10 1 C1 02 C02 02 C 2 2 C02 2 C 2
( 10C 0 1C 0 20C 0 2C 0 10 С 1 С 20 С 2 С )
Величинами второго порядка малости ( · ) пренебрегаем. Получим:
d C
V0
10 C1 C10 1 10 C10 02 C 2 C 02 2 02 C 02
d
10 02 C C 0 1 C 0 2 10 02 C 0 ;
V0
d t
10 t1 t10 1 10 t10 02 t 2 t 02 2 02 t 02
d
10 02 t t 0 1 t 0 2 10 02 t 0 ;
S0
d h
( 10 1 ) ( 02 2 ) ( 0 ) .
d
8

9.

Шаг 2
Вычтем из данных уравнений соответствующие уравнения статики:
0 10 C10 02 C02 10 02 C0 ,
0 10 t10 02 t 02 10 02 t 0 ,
0 10 02 0 .
Получим:
d C
10 C1 02 C 2 (C10 C 0 ) 1 (C 02 C 0 ) 2 10 02 C
d
d t
V0
10 t1 02 t 2 ( t10 t 0 ) 1 ( t 02 t 0 ) 2 10 02 t
d
d h
S0
1 2 .
d
V0
9

10.

Шаг 3
Рассортируем
переменные.
Слева
–
выходные;
справа
–входные.
Линеаризованные уравнения примут вид:
d C
10 02 C 10 C1 02 C2 C10 C0 1 C02 C0 2 ;
d
d t
V0
10 02 t 10 t1 02 t 2 t10 t 0 1 t 02 t 0 2 :
d
d h
S0
1 2 .
d
V0
10

11.

Шаг 4
Поделим левые и правые части первых двух уравнений на 10 02 , получим:
d C
T1
C K11 C1 K12 C 2 K13 1 K14 2 ,
d
(4)
d t
T2
t K 21 t1 K 22 t 2 K 23 1 K 24 2 ,
d
d h
T3
1 2 ,
d
V0
10
02
C10 C0
C02 C0
T1 0
; K11 0
; K12 0
; K13 0
; K14 0
0
0
0
0
1 2
1 2
1 2
1 2
1 02
V0
10
02
t10 t 0
t 02 t 0
T2 0
; K 21 0
; K 22 0
; K 23 0
; K 24 0
0
0
0
0
1 2
1 2
1 2
1 2
1 02
T3 S 0 ; .
Начальные условия: C 0 0 , t 0 0 , h 0 0 .
Система уравнений (4) представляет собой математическую модель объекта в
линеаризованной форме.
11

12.

Обозначим правые части уравнений (4) f i :
f1 K11 C1 K12 C 2 K13 1 K14 2 ;
f 2 K 21 t1 K 22 t 2 K 23 1 K 24 ;
f 3 1 2 .
Тогда система уравнений (4) запишется более компактно:
d C
T1
C f1 ,
d
d t
T2
t f 2 ,
d
d h
T3
f 3 ,
d
(5)
Начальные условия: C 0 0 , t 0 0 , h 0 0 .
Поученная
система
является
системой
линейных
обыкновенных
дифференциальных уравнений с нулевыми начальными условиями.
12

13.

Шаг 5
Преобразуем полученные уравнения по Лапласу:
ˆ C
ˆ fˆ ,
T p C
1
1
T2 p t̂ t̂ fˆ2 ,
T p hˆ fˆ .
3
3
Ĉ, t̂ , ĥ, f̂ i –
где
р–
комплексная
переменная,
изображения
соответствующих переменных.
Передаточные функции объекта по каналам запишутся:
ˆ
C
1
W1 (p)
,
ˆ
f1 T1 p 1
(6)
ˆ
t
1
W2 (p)
.
ˆ
T
p
1
2
f 2
hˆ
1
W3 ( p)
fˆ3 T3 p
В этих выражениях
ˆ K C
ˆ K ˆ K ˆ ,
fˆ1 K11 C
1
12
2
13
1
14
2
(7)
ˆ
f K t̂ K t̂ K ˆ K ˆ .
2
21
1
22
2
23
1
24
2
fˆ3 ˆ 1 ˆ 2 ˆ .
13

14.

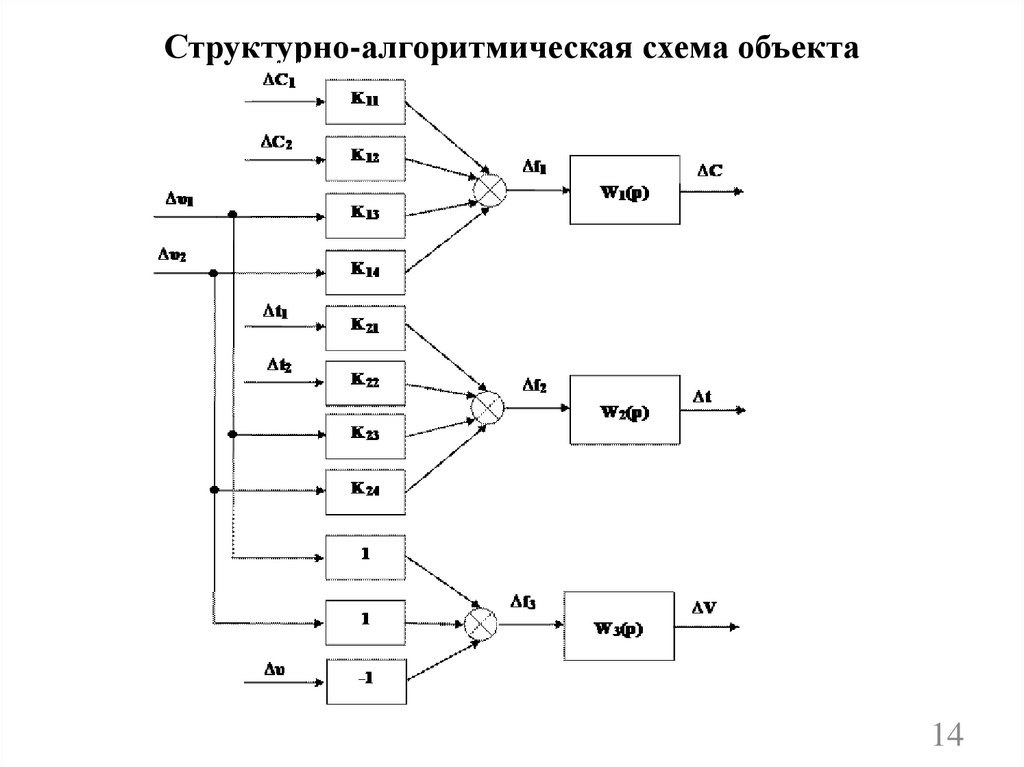
Структурно-алгоритмическая схема объекта
14

15.

Аппроксимация объекта типовыми динамическими
звеньями
При наличии структурно-алгоритмической схемы объекта можно
получить передаточную функцию по любому каналу.
Например, получим передаточную функцию по каналу 2 → С
В соответствии с правилами блок-алгебры при последовательном
соединении элементов, их передаточные функции перемножаются. При
движении от 2 к С получим: