Призма. Пирамида. Решение задач (9 класс)

1.

Призма. Пирамида.
Решение задач.
Геометрия, 9 класс

2.

Учащийся должен:
знать и применять формулы
площадей призмы и пирамиды,
при решении задач;
знать и применять формулы
объема призмы и пирамиды,
при решении задач.

3.

Параллелепипед

4.

Призма
Призма — многогранник, две грани которого (основания) —
равные многоугольники, лежащие в параллельных плоскостях, а
боковые грани — параллелограммы.

5.

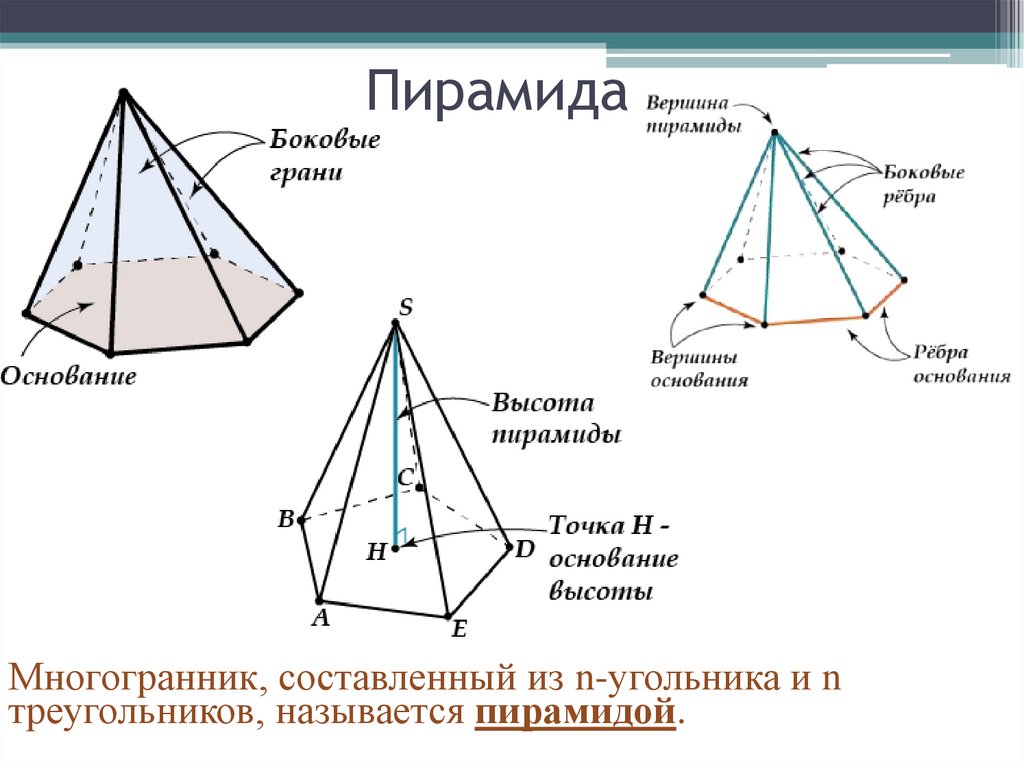
Пирамида
Многогранник, составленный из n-угольника и n
треугольников, называется пирамидой.

6.

Решим задачи

7.

Основанием прямой треугольной призмы служит
прямоугольный треугольник с катетами 6 и 8, высота призмы
равна 10. Найдите площадь ее поверхности.
Решение:
Sпол.поверхности = 2S осн + S бок.
1). В основании прямоугольный треугольник,
S осн = ½ ab=
2). S бок= ah + bh + ch = (a+b+c)h= Pосн h
По теореме Пифагора : с=
S бок=
3). S п.п.=
Ответ. 288 кв. ед.

8.

SО – высота пирамиды SABC.
Таким образом, OS =
Ответ: ____________

9.

В правильной четырехугольной пирамиде SABCD точка O –
центр основания, S – вершина, SO=15см , BD=16см. Найдите
боковое ребро SA.
Решение:
В правильной пирамиде вершина
проецируется в центр основания, то О –
точка пересечения диагоналей квадрата.
Следовательно, SO является высотой
пирамиды.
Тогда по теореме Пифагора…
Ответ: ___________

10.

В правильной треугольной пирамиде SABC точка M – середина
ребра AB, S – вершина. Известно, что BC = 3см, а площадь
боковой поверхности пирамиды равна 45 см. Найдите длину
отрезка SM.
Решение:
Найдем площадь грани SAB:
Ответ: 10 см.

11.

2. Основанием прямой треугольной призмы служит
прямоугольный треугольник с катетами 3 и 4, высота
призмы равна 10. Найдите площадь ее поверхности.