Корреляционно-фильтровые методы обработки когерентных сигналов. Лекция № 13

1.

2.

Военный учебный центр
им. Героя Российской Федерации
генерала армии Дубынина В.П.
Дисциплина
«Основы теории радиолокационных
систем и комплексов»
1

3.

Лекция № 13
«Корреляционно-фильтровые методы
обработки когерентных сигналов»
2

4.

Учебная цель:
1. Раскрыть содержание принципа корреляционнофильтровой обработки когерентных сигналов и
дать характеристику структурным схемам и
физическим процессам такой обработки.
3

5.

Вопросы лекции:
1. Корреляционно-фильтровая обработка сигналов на
фоне белого шума.
2. Время-частотная
функция
рассогласования
одиночного радиоимпульса. Сечения АКФ и их
анализ.
3. Время-частотная
функция
рассогласования
сигналов с ЛЧМ. Достоинства ЛЧМ сигналов.
4. Желаемая функция рассогласования. Времячастотная функция рассогласования сигналов с
фазовой манипуляцией.
4

6.

Литература
для самостоятельной работы:
1. Радиолокационные системы: учебник / В.П.
Бердышев, Е.Н. Гарин, А.Н. Фомин [и др.]; под
общ. ред. В.П. Бердышева. – Красноярск : Сиб.
федер. ун-т. -2011. -400с..
2. Бакулев П.А. Радиолокационные системы:
учебник для вузов.М.: Радиотехника, 2004,
320с.,ил.
5

7.

Учебный вопрос № 1
Корреляционно-фильтровая обработка сигналов
на фоне белого шума.
6

8.

Вопрос № 1
В каждом из вариантов оптимальной обработки при
обнаружении сигналов, рассмотренных на предыдущих
лекциях, встречается вычисление корреляционных интегралов:
либо напрямую, либо с помощью согласованного с сигналом
фильтра. Часто на практике оказывается проще для этих целей
использовать одновременно операции корреляционного и
фильтрового вычисления корреляционного интеграла. Такая
обработка сигналов называется корреляционно-фильтровой.
Она предусматривает представление ожидаемого
сигнала в виде произведения двух сигналов, один из которых
используется для корреляции, а другой определяет импульсную
характеристику согласованного фильтра (СФ). Конкретная
схема корреляционно-фильтрового обнаружителя определяется
многими факторами, зависящими от решаемых РЛС задач, ее
технических характеристик, вида используемого сигнала и т.д.
7

9.

Вопрос № 1
Оптимальное обнаружение радиолокационных сигналов x(t)
основано на вычислении корреляционного интеграла.
z y t x t y t dt .
Это вычисление может быть произведено или непосредственно с
помощью перемножителя и интегратора (корреляционный метод), или с
помощью согласованного фильтра (фильтровой метод).
Корреляционные схемы обеспечивают оперативную смену
обрабатываемых сигналов, но многоканальны при неизвестных t3 и Fq.
Причем в случае приема сигналов со случайными параметрами каждый
канал должен дополнительно содержать 2 квадратурных канала.
СФ инвариантны ко времени прихода обрабатываемых сигналов,
однако исключают возможность оперативного изменения вида
обрабатываемых сигналов и сложны в реализации для случая обработки
квазинепрерывных и широкополосных импульсных сигналов.
8

10.

Вопрос № 1
Достоинства корреляционного и фильтрового обнаружителей в значительной
степени могут быть реализованы в корреляционно-фильтровом обнаружителе.
Принцип корреляционно-фильтровой обработки заключается в представлении
ожидаемого сигнала x(t) в виде произведения двух функций, x1(t) и x2(t), т.е.
x(t)= x1(t) x2(t), и в вычислении с их помощью корреляционного интеграла.
z y t y t x 1 t x 2 t dt .
Выбор функций x1(t) и x2(t) производится таким образом, чтобы функция x2(t)
обеспечивала простоту технической реализации импульсной характеристики
согласованного фильтра k2(t)=c x2(t0-t).
Этот метод обработки сводится к двум операциям:
перемножению
принимаемого
сигнала
y(t)
с
функцией
x1(t)
(Элемент корреляционной обработки):
y1(t)= y(t)x1(t);
9

11.

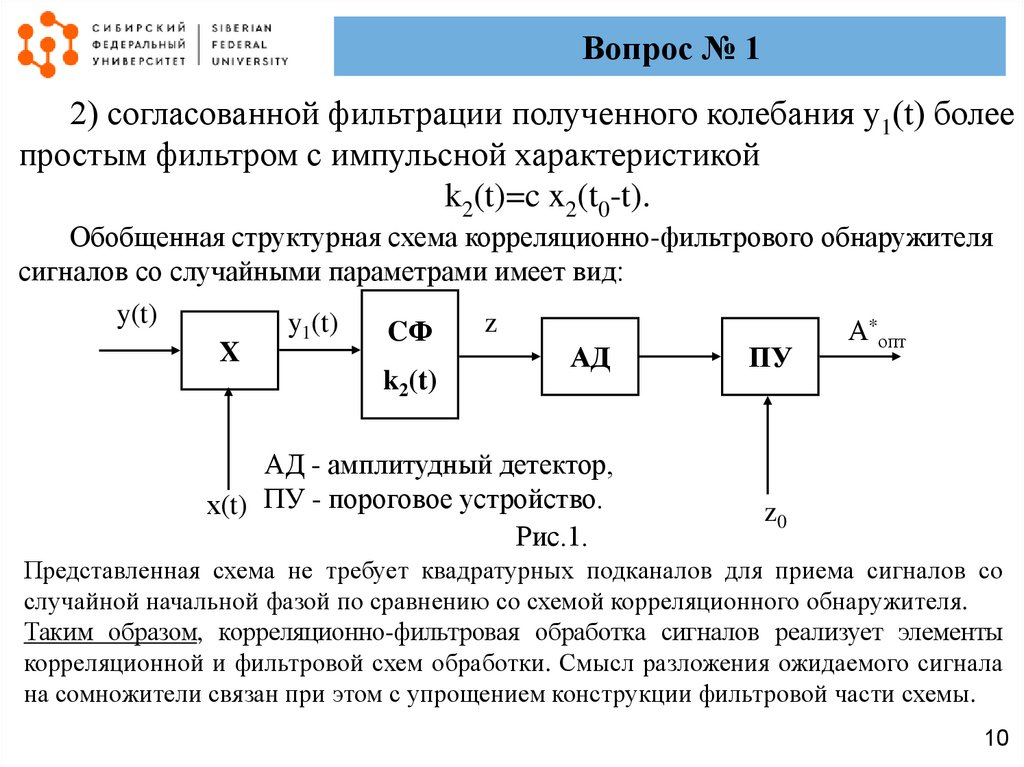
Вопрос № 1
2) согласованной фильтрации полученного колебания y1(t) более
простым фильтром с импульсной характеристикой
k2(t)=c x2(t0-t).
Обобщенная структурная схема корреляционно-фильтрового обнаружителя
сигналов со случайными параметрами имеет вид:
y(t)
y1(t)
z
А*опт
CФ
X
АД
ПУ
k2(t)
АД - амплитудный детектор,
х(t) ПУ - пороговое устройство.
Рис.1.
z0
Представленная схема не требует квадратурных подканалов для приема сигналов со
случайной начальной фазой по сравнению со схемой корреляционного обнаружителя.
Таким образом, корреляционно-фильтровая обработка сигналов реализует элементы
корреляционной и фильтровой схем обработки. Смысл разложения ожидаемого сигнала
на сомножители связан при этом с упрощением конструкции фильтровой части схемы.
10

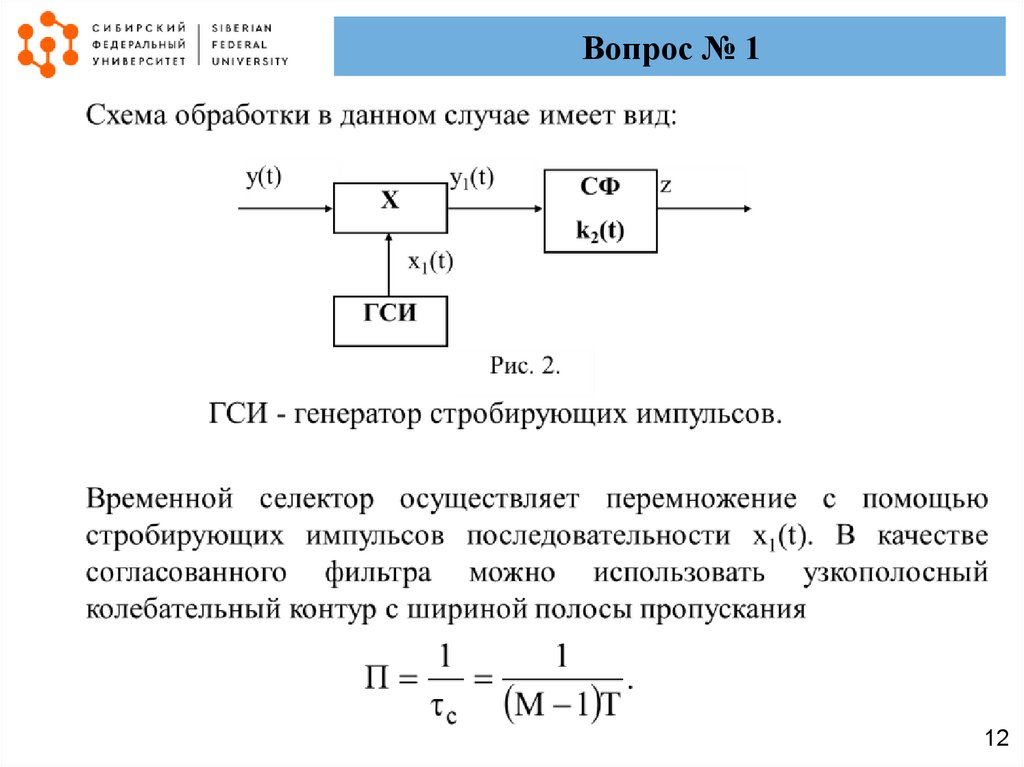
12.

Вопрос № 1
11

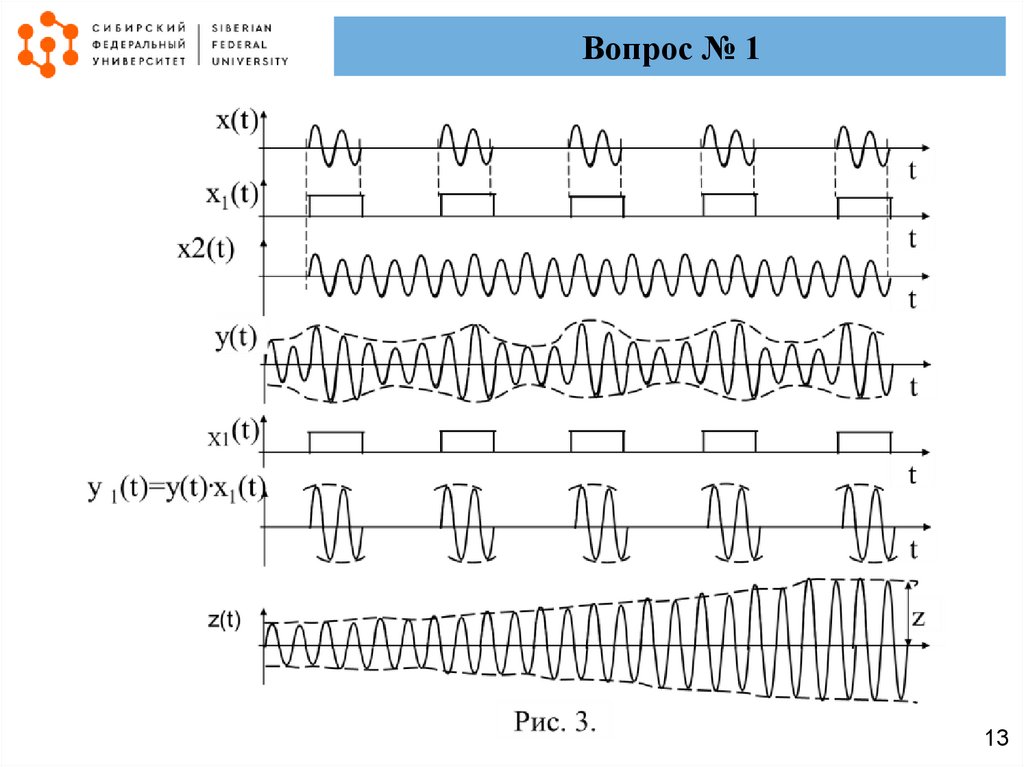
13.

Вопрос № 1
12

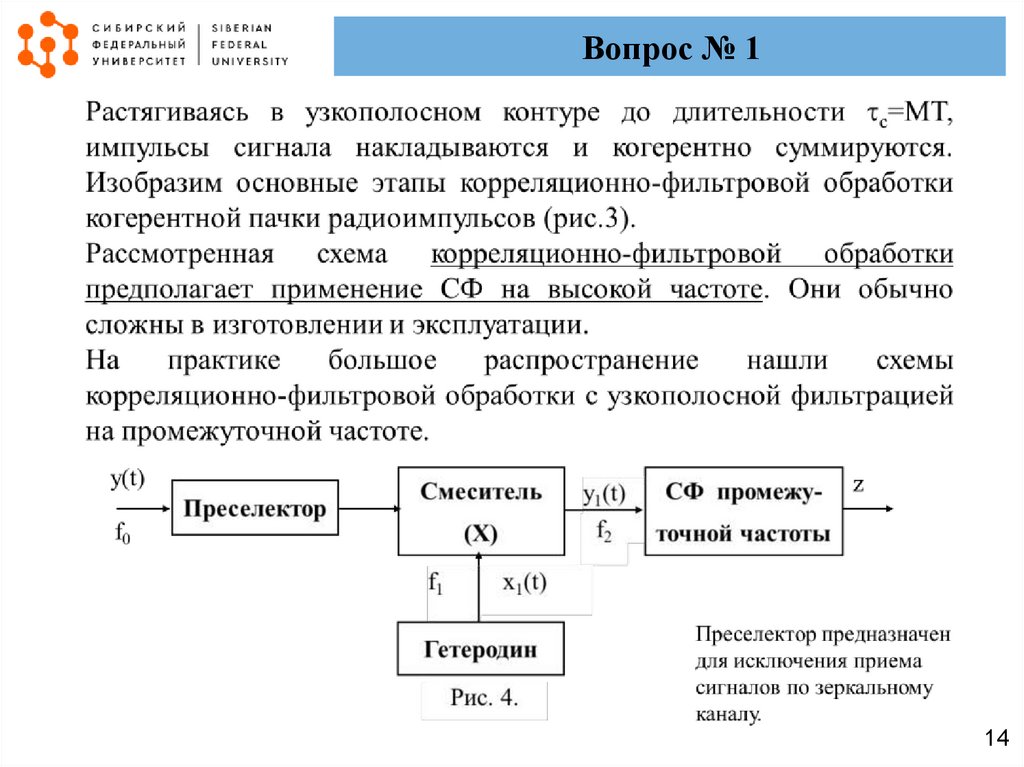
14.

Вопрос № 1
13

15.

Вопрос № 1
14

16.

Вопрос № 1
Структурная схема вытекает из комплексного представления
ожидаемого сигнала
x t e
j2 f0 t
x 1 t e
j2 f1t
x 2 t e
j2 f 2 t
и соответствует:
1)обобщенному гетеродинированию на частоте f1=fг с введением в
гетеродинное напряжение модулирующего множителя x
t
1
2) фильтровой обработке на промежуточной частоте f2=fпр. ИХ
фильтра согласуется с колебанием
x 2 t e
j2 f 2 t
x t j2 f0 f1 t
e
.
x 1 t
15

17.

Учебный вопрос №2
Время-частотная функция рассогласования
одиночного радиоимпульса. Сечения АКФ и их
анализ.
16

18.

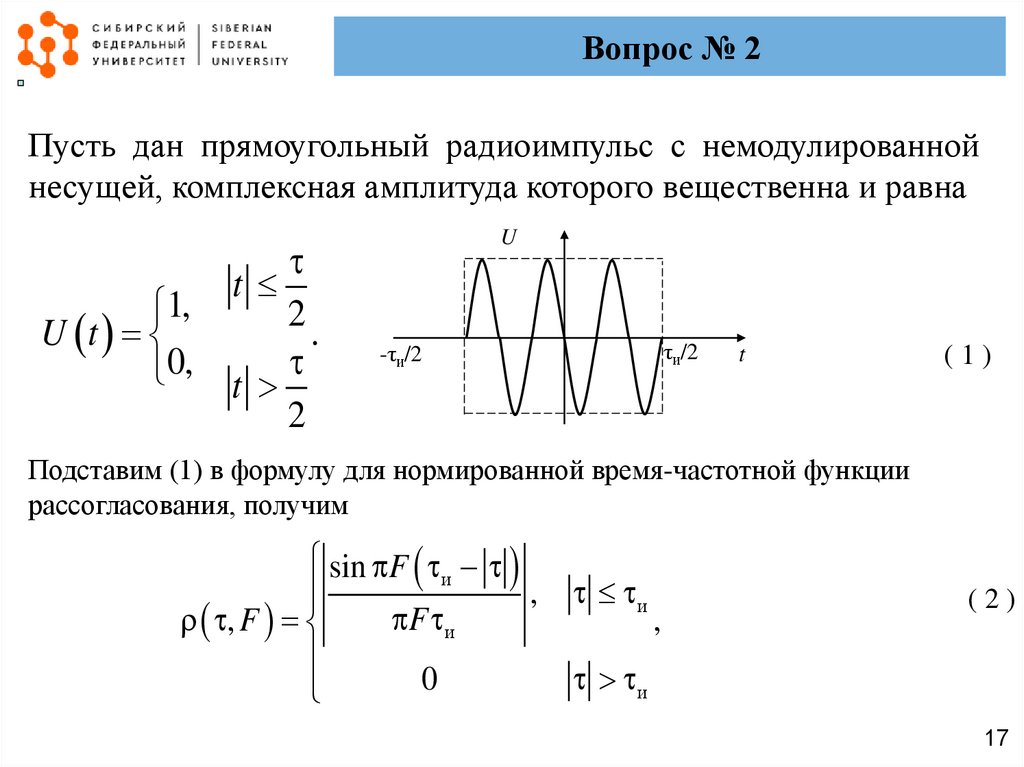
Вопрос № 2
Пусть дан прямоугольный радиоимпульс с немодулированной
несущей, комплексная амплитуда которого вещественна и равна
1,
U t
0,
t
2.
t
2
U
τи/2
-τи/2
t
(1)
Подставим (1) в формулу для нормированной время-частотной функции
рассогласования, получим
sin F и
,
F и
, F
0
и
,
(2)
и
17

19.

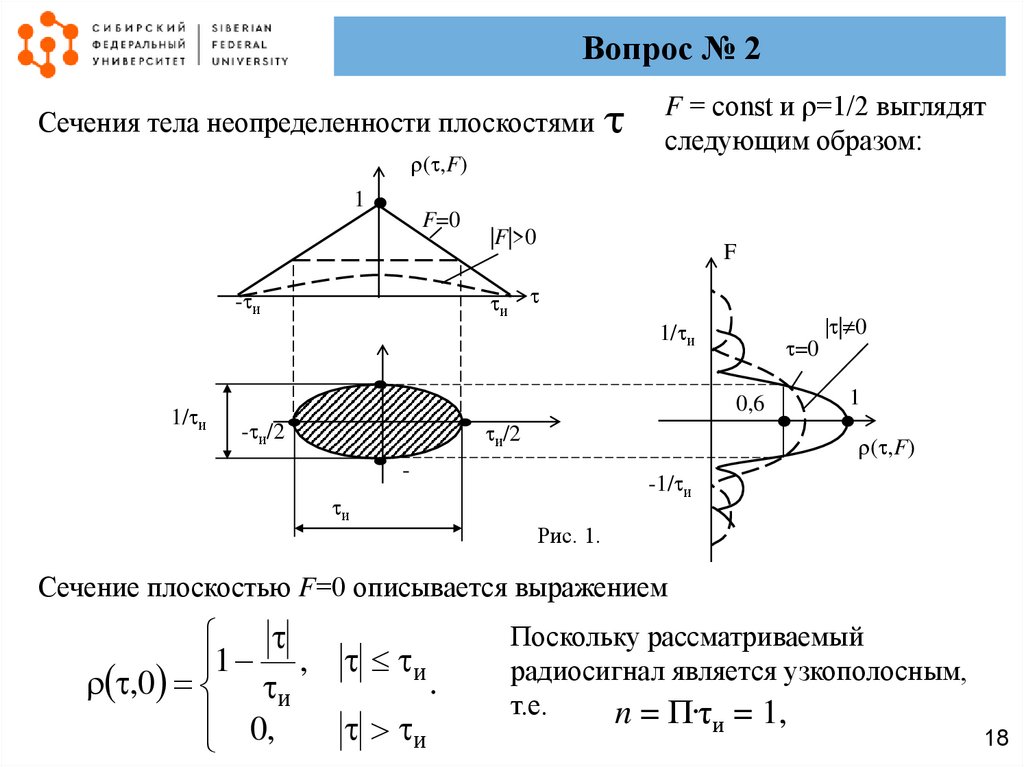
Вопрос № 2
Сечения тела неопределенности плоскостями
( ,F)
F = const и ρ=1/2 выглядят
следующим образом:
1
F=0
|F|>0
F
и
- и
1/ и
1/ и
=0
0,6
и/2
- и/2
| 0
1
( ,F)
-
-1/ и
и
Рис. 1.
Сечение плоскостью F=0 описывается выражением
1 ,
,0 и
0,
и
и
.
Поскольку рассматриваемый
радиосигнал является узкополосным,
т.е.
n = П.τ = 1,
и
18

20.

Вопрос № 2
то мера разрешающей способности по времени запаздывания и
дальности равна 1 ,
и
П
c
c
c
r
и .
2
2П 2
Она зависит от ширины спектра сигнала. Зависимость ρ от τ для
различных F=const можно рассматривать как кривые огибающих
напряжений на выходе оптимального фильтра при расстройке
F по несущей частоте. Расстройка ведет к уменьшению пикового
значения и к искажению формы огибающей (рис.1).
Сечение АКФ плоскостью τ=0
sin F и
0, F
,
F и
представляет собой энергетический спектр огибающей
1, 2
прямоугольного радиоимпульса.
F
Его протяженность на уроне 0,5 оценивается величиной
и 19

21.

Вопрос № 2
20

22.

Вопрос № 2
21

23.

Вопрос № 2
Огибающая сигнала в виде прямоугольной когерентной пачки прямоугольных
радиоимпульсов описывается соотношением
и
1, t mT 2
U t
,
0, t mT и
2
Параметры пачки и импульсов:
τи - длительность каждого
радиоимпульса;
T - период их повторения;
M - число импульсов в пачке;
T0=MT - длительность пачки.
22

24.

Вопрос № 2
Ширина спектра такого сигнала равна П = 1/τи и поскольку
T0 = MT и n П Т 0 M T 1,
и
то этот сигнал следует считать широкополосным.
Функция рассогласования имеет отличные от нуля значения в
пределах временного интервала -MT< τ <MT, в котором
описывается соотношением:
sin M m FT
mT , F ,
, F
0
M sin FT
m M 1
M 1
функция
рассогласования
(2)
одиночного
где , F прямоугольного когерентного радиоимпульса без
наружных знаков модуля.
Сечения тела и диаграмма неопределенности ρ=0,5
имеют вид
23

25.

Вопрос № 2
ρ
Δτ = τи
Т
δF=1,2/MT
F
-τи
τ
τи
2МТ
ρ(F,0)
2/τи
Т
ρ
1/Т
τ
1/Т
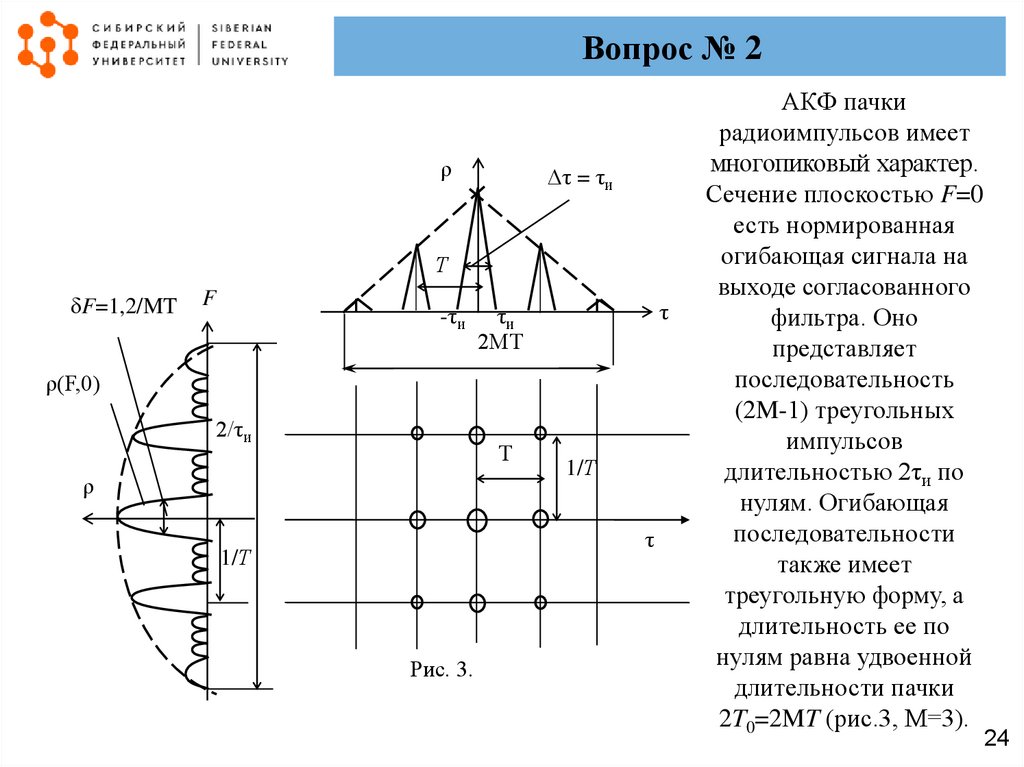
Рис. 3.
АКФ пачки
радиоимпульсов имеет
многопиковый характер.
Сечение плоскостью F=0
есть нормированная
огибающая сигнала на
выходе согласованного
фильтра. Оно
представляет
последовательность
(2M-1) треугольных
импульсов
длительностью 2τи по
нулям. Огибающая
последовательности
также имеет
треугольную форму, а
длительность ее по
нулям равна удвоенной
длительности пачки
2T0=2MT (рис.3, M=3).
24

26.

Вопрос № 2
25

27.

Вопрос № 2
26

28.

Вопрос № 2
F
Fд макс
Fд макс
tз макс
τ
tз макс
В РЛС обнаружения целей параметры принимаемых сигналов всегда будут
лежать в пределах этого прямоугольника, если поиск целей ведется в пределах
априорного распределения.
Наложим прямоугольник на диаграмму неопределенности сигнала. Если при
этом внутри прямоугольника окажется единственный центральный пик АКФ,
то измерения в РЛС будут однозначны. Для этого необходимо выполнение двух
1
неравенств.
tзмакс T
Fдмакс
Выполнить это условие обычно не удается, поэтому допускают
неоднозначность оценок в зависимости от характера решаемых задач и условий,
в которых работает РЛС.
Так, при T > tзмакс в РЛС обеспечивается
1
однозначное измерение дальности, а при T
- скорости.
27
F
дмакс

29.

Вопрос № 2
Неоднозначность
измерений
обычно
устраняют
периодическим изменением параметров зондирующего
сигнала (T,f0), либо одновременным облучением целей
сигналами с различными параметрами.
Таким
образом,
с
помощью
последовательности
радиоимпульсов можно, уменьшая длительность отдельного
радиоимпульса τи, повысить разрешение по дальности, а
увеличивая число импульсов в пачке М, добиться требуемой
разрешающей способности по скорости. Однако времячастотная функция рассогласования когерентной пачки
радиоимпульсов является многопиковой и платой за
повышение разрешающей способности РЛС по скорости
является неоднозначное измерение дальности и скорости.
28

30.

Учебный вопрос №3
Время-частотная функция рассогласования
сигналов с ЛЧМ. Достоинства ЛЧМ сигналов.
29

31.

Вопрос № 3
30

32.

Вопрос № 3
31

33.

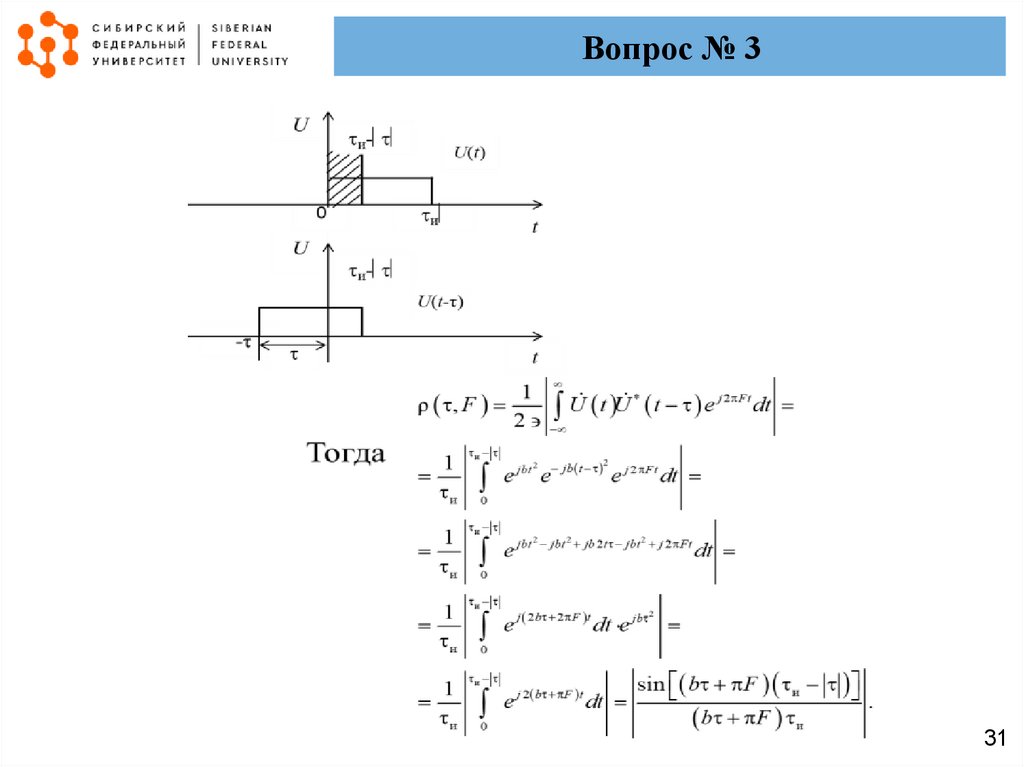
Вопрос № 3
Таким образом, данный радиоимпульс имеет следующую АКФ:
sin
F
f
и
и
,
(1)
и
, F
.
F
f
и
и
0,
и
Сечения тела неопределенности плоскостью F = const, и
неопределенности имеют вид:
=0
F
F
F=0
F
2 и
= const и диаграмма
a)
2 f
=0,5
f 1/ и
и
2 и
б)
32

34.

Вопрос № 3
33

35.

Вопрос № 3
F
F
1/ и=П
П= f
При обработке ЛЧМ сигналов в СФ происходит их сжатие, что характеризуется сечением ρ
( ,0).
Скос диаграммы неопределенности ЛЧМ радиоимпульса в координатах ,F обусловливает
неопределенность дальность-скорость, проявляющуюся во времени смещениями сжатого
импульса при частотной расстройке ΔF на время
и
F ,
f
(3)
df
Знак «-» соответствует положительному наклону dt 0 «пика частотной модуляции»,
знак «+» - отрицательному наклону. Поэтому при наличии двух сигналов, отличающихся
по доплеровской частоте на величину ΔF и имеющих взаимное запаздывание и F ,
f
они становятся практически не разрешимыми (при условии │Δ F│< Δ f).
34

36.

Вопрос № 3
Для устранения неопределенности «дальность-скорость» могут
использоваться, например, два ЛЧМ радиоимпульса, имеющие
противоположные законы изменения частоты, или один ЛЧМ
радиоимпульс с симметричным законом ее изменения.
f
f
fmax
fmax
fmin
fmin
и
t
и/2
t
и
35

37.

Учебный вопрос №4
Желаемая функция рассогласования. Времячастотная функция рассогласования сигналов с
фазовой манипуляцией
36

38.

Вопрос № 4
37

39.

Вопрос № 4
По условию задачи требуется обеспечить Vпик<<1. Этому соответствует случай
τи ·П = n >>1,
(7)
Сигналы, для которых выполняется это условие, называют широкополосными, а
АКФ, подобную рассмотренной, называют игольчатой или кнопочной.
Таким образом, сигнал, обладающий одновременно высокими разрешающими
способностями по времени запаздывания и частоте, должен быть
широкополосным.
Уровень остатков найдем из (4) с учетом (6), полагая Vпик = 0
V Vост
2
или
2
ост
2 и 2П 1
ост
1
1
.
2 и П 2 n
Наличие остатков (боковых лепестков) затрудняет выделение
слабых сигналов на фоне сильных. Для улучшения наблюдения
слабых сигналов необходимо увеличить базу сигналов n = и · П.
В наибольшей степени удовлетворяют требованиям кнопочной
38
АКФ ФМ сигналы.

40.

Вопрос № 4
• В радиолокации находят применение импульсные и непрерывные
фазоманипулированные радиосигналы.
• Рассмотрим вначале радиоимпульсы с внутриимпульсной фазовой
манипуляцией 0, фазы.
• Радиоимпульс длительностью и состоит из n примыкающих парциальных
радиоимпульсов длительностью Комплексная амплитуда ФМ сигнала с
манипуляцией 0, действительна. Запишем комплексную амплитуду первого
парциального импульса в виде
1, 0 t 0
U0 t U0 t
.
0, t 0, t 0
Тогда комплексная
выражением
амплитуда
ФМ
сигнала
опишется
n 1
U t qiU 0 t i 0 ,
i 0
(8)
где последовательность qi в виде ±1 описывает код сигнала.
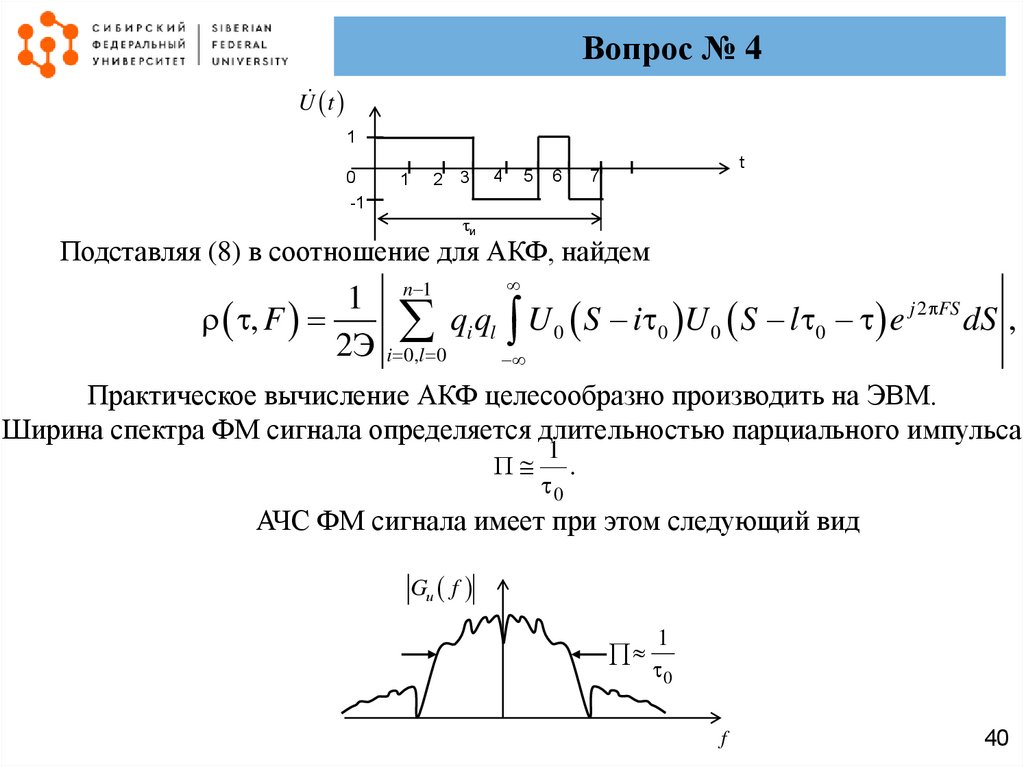
Например, для радиоимпульса, манипулированного семиэлементным кодом Баркера,
такая последовательность имеет вид 111 -1-1 1-1. Соответственно его комплексная
амплитуда изображается таким образом:
39

41.

Вопрос № 4
U t
1
0
-1
1
2
3
4
5
6
t
7
и
Подставляя (8) в соотношение для АКФ, найдем
1 n 1
j 2 FS
, F
q
q
U
S
i
U
S
l
e
dS ,
i l
0
0
0
0
2Э i 0,l 0
Практическое вычисление АКФ целесообразно производить на ЭВМ.
Ширина спектра ФМ сигнала определяется длительностью парциального импульса
П
1
.
0
АЧС ФМ сигнала имеет при этом следующий вид
Gи f
1
0
f
40

42.

Вопрос № 4
τи
τи П
n,
Следовательно
и ФМ сигнал будет широкополосным при
τ0
достаточно большом числе парциальных импульсов.
Если n >> 1, а кодообразующая последовательность достаточно "хаотичная", то
сигнал называют шумоподобным и он имеет кнопочную АКФ. Главный пик
АКФ находится в начале координат, а его размеры по осям , F определяют
меры разрешающей способности по времени запаздывания
1
0
П
1
F , (на уровне ρ(0,F) = 0,64).
и частоте
и
Уровень остатков за пределами главного пика составляет ост
1
.
n
При сравнительно малом n меньший уровень остатков в сечении АКФ
плоскостью F=0 обеспечивают коды Баркера:
1
ост .
n
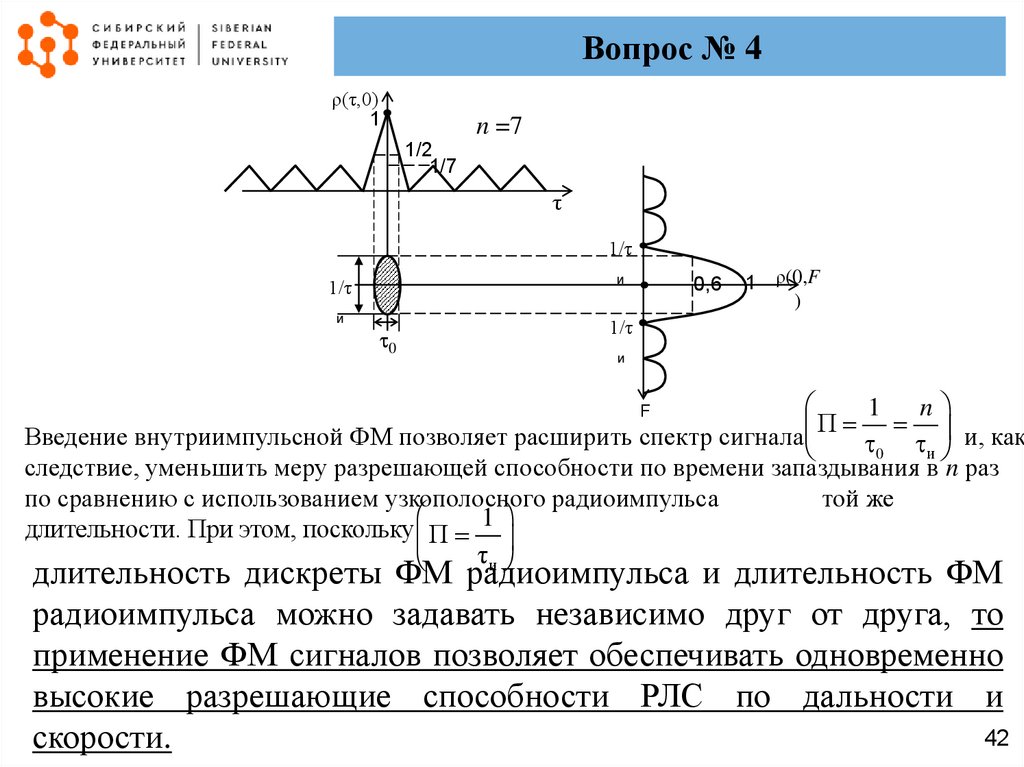
Сечения АКФ для ФМ семиэлементным кодом Баркера сигнала имеют вид
41

43.

Вопрос № 4
ρ(τ,0)
1
n =7
1/2
1/7
τ
1/τ
и
1/τ
и
0
0,6
1 ρ(0,F
)
1/τ
и
1 n
П
Введение внутриимпульсной ФМ позволяет расширить спектр сигнала
0 и и, как
следствие, уменьшить меру разрешающей способности по времени запаздывания в n раз
по сравнению с использованием узкополосного радиоимпульса
той же
1
длительности. При этом, поскольку П
τи
F
длительность дискреты ФМ радиоимпульса и длительность ФМ
радиоимпульса можно задавать независимо друг от друга, то
применение ФМ сигналов позволяет обеспечивать одновременно
высокие разрешающие способности РЛС по дальности и
42
скорости.

44.

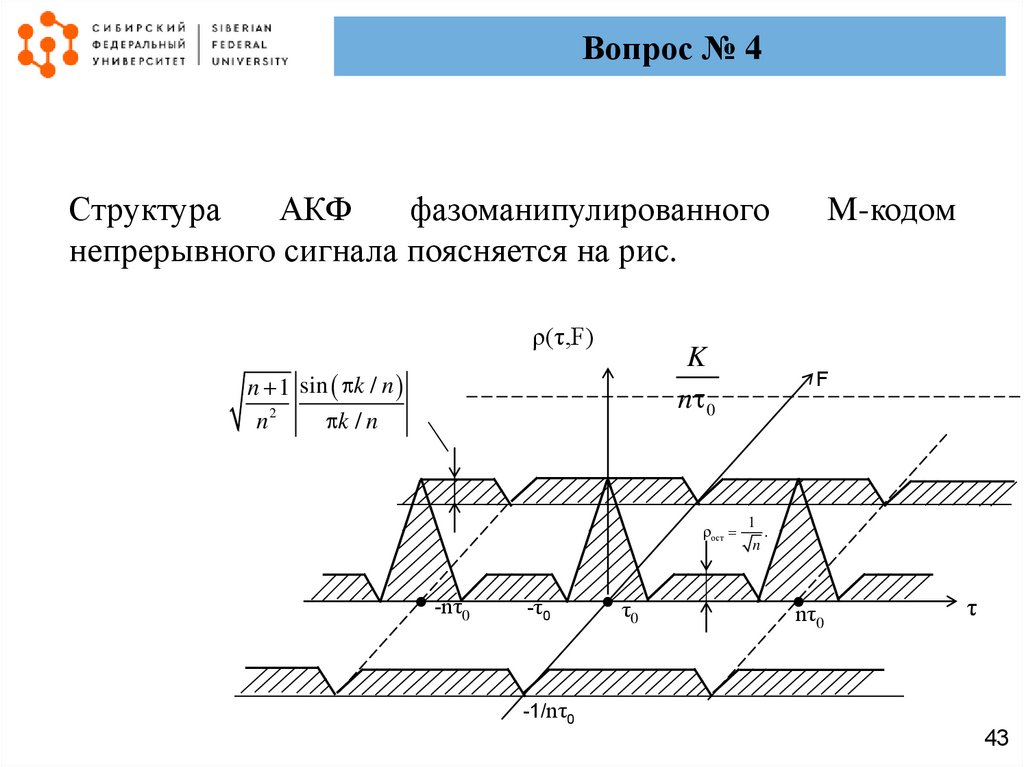
Вопрос № 4
Структура
АКФ
фазоманипулированного
непрерывного сигнала поясняется на рис.
ρ(τ,F)
K
n 0
n 1 sin k / n
n2
k / n
ост
-nτ0
-τ0
τ0
M-кодом
F
1
.
n
nτ0
τ
-1/nτ0
43

45.

Вопрос № 4
Она состоит из стянутых в δ-функцию по оси F (в
силу теоретически неограниченной длительности
сигнала) и протяженных по оси взаимно
параллельных плоских элементов. Остатки на оси
соответствуют уровню
, на остальной части тела
неопределенности их уровень при n >>1 около 1 n
44

46.

Вопрос № 4
• введение внутриимпульсной модуляции
позволяет расширить спектр сигнала и
обеспечить одновременно высокие
разрешающие способности РЛС по дальности и
скорости. Шумоподобный ФМ сигнал имеет
"кнопочную" АКФ с уровнем боковых лепестков
(остатков)
1
ост
.
n
45

47.

Заключение:
1. Применение линейной частотной модуляции и фазовой
манипуляции сигнала позволяет расширить спектр сигнала и за счет
независимого выбора его длительности обеспечить одновременно
высокие разрешающие способности РЛС по дальности и скорости.
2. Скос ДН ЛЧМ сигнала может приводить к скоростной ошибке,
т.е. неопределенности "дальность-скорость". Для её устранения могут
использоваться,
например,
ЛЧМ
радиоимпульсы,
имеющие
противоположные законы изменения частоты.
3. Для обеспечения высоких разрешающих способностей по
дальности и скорости идеальный сигнал должен быть широкополосным с
игольчатой функцией рассогласования и равномерным уровнем остатков.
В наибольшей степени этим требованиям удовлетворяют ФМ сигналы.
4. При хаотическом законе фазовой манипуляции сигнал
является шумоподобным и имеет "кнопочную" АКФ. Хорошими
автокорреляционными свойствами обладают непрерывные сигналы,
манипулированные М-последовательностями.
46

48.

Задание на самостоятельную подготовку:
• Литература
• ОСНОВНАЯ
• 1. Информационные технологии в радиотехнических системах:
Учебное пособие/ В.А.Васин, И.Б.Власов, Ю.М.Егоров и др.; под ред.
И.Б.Федорова. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2003. Л 1/о с.214225;
• ДОПОЛНИТЕЛЬНАЯ
• 1. Теоретические основы радиолокации. Под редакцией Ширмана
Я.Д. Учебное пособие для вузов. М., Изд-во «Советское радио».
1970, Л 1/д с.343-349, 378-393;
• 2. Основы радиолокации и радиоэлектронная борьба. А.Е.Охрименко.
Учебник. М., «Воениздат», 1983, Л 2/д с.33-42.
47

49.

Спасибо за внимание
48