Похожие презентации:
Закон сохранения импульса. Лекция 2
1.
ЧУЕВ Анатолий Степановичдоцент кафедры ФН-4
http://wwv.bmstu.ru/ps/~chuev/
Персональная страница Чуева А.С.
Сайт кафедры «Физика» (ФН-4):
http://fn.bmstu.ru/tm-fs-4
2. Лекция 2. «Закон сохранения импульса»
• Масса, импульс (количество движения)• Силы.
• Инерциальная система отсчета
• Динамика материальной точки
• Механическая система (МС) и ее центр масс
• Уравнение изменения импульса МС
• Закон сохранения импульса
А.С. Чуев. 2024 г.
2
3.
Мир каждый видит в облике ином и каждыйправ – так много смысла в нём.
Гёте.
Истинное знание есть знание причин
Аристотель
А.С. Чуев. 2024 г.
3
4.
Я не знаю, что мир думает обо мне; себесамому я кажусь всего лишь мальчиком,
играющим на берегу, возвращающим себя
в настоящее, но потом находящим гладкий
камешек или необычайно красивую ракушку,
- в то время как великий океан непостижимой
истины простирается передо мной"
(Исаак Ньютон)
А.С. Чуев. 2024 г.
4
5.
Первый закон Ньютона – закон инерции• всякая материальная точка (тело)
сохраняет состояние покоя или
равномерного прямолинейного
движения до тех пор, пока
воздействие со стороны других тел
не заставит её (его) изменить это
состояние.
А.С. Чуев. 2024 г.
5
6. Инерциальная система
Систему отсчета называют инерциальной,если свободная частица, не подверженная
действию никаких других тел, движется в
ней прямолинейно и равномерно, или, как
говорят, по инерции.
7.
Принцип относительности Галилея:• все инерциальные системы по своим
механическим свойствам эквивалентны друг
другу. Это значит, что никакими механическими
опытами, проводимыми "внутри" данной
инерциальной системы, нельзя установить,
покоится эта система отсчета или движется. Во
всех инерциальных системах отсчета свойства
пространства и времени одинаковы, одинаковы
также и все законы механики.
А.С. Чуев. 2024 г.
7
8.
Не срисовыватьПреобразования Галилея:
при
А.С. Чуев. 2024 г.
8
9. Масса
• Инертная масса (кг)• Гравитационная (кинематическая) масса
измеряется в (м3/с2)
• Гравитационная постоянная G – это
соотношение инертной и гравитационной
масс (G в LT-системе безразмерная величина)
G 6,67 10
11
м
с 2 кг
3
3-й закон
Кеплера:
Масса величина аддитивная m
А.С. Чуев. 2024 г.
R 3 Gmc
2
T
4 2
m
i
9
10. Импульс
P mv Ftкг
м
Единица измерения
с
1
Размерность MLT
F ma
Сила
Единица измерения
Размерность
MLT
2
кг м
2
с
А.С. Чуев. 2024 г.
10
11. Второй закон Ньютона
F ma• Масса - мера инертности материальных тел
• Инертность - свойство, выражающее степень
сопротивления тела к изменению его скорости
dP
F
dt
существуют инерциальные системы отсчета
(ИСО), где импульс частицы сохраняется при
отсутствии действия других тел.
Принцип суперпозиции сил
А.С. Чуев. 2024 г.
11
12. Третий закон Ньютона
• Силы, с которыми две материальные точкивоздействуют друг на друга, всегда равны по
модулю и направлены в противоположные
стороны вдоль прямой, соединяющей эти
точки
Согласно этому закону, взаимодействие между
телами распространяется в пространстве с
бесконечно большой скоростью
А.С. Чуев. 2024 г.
12
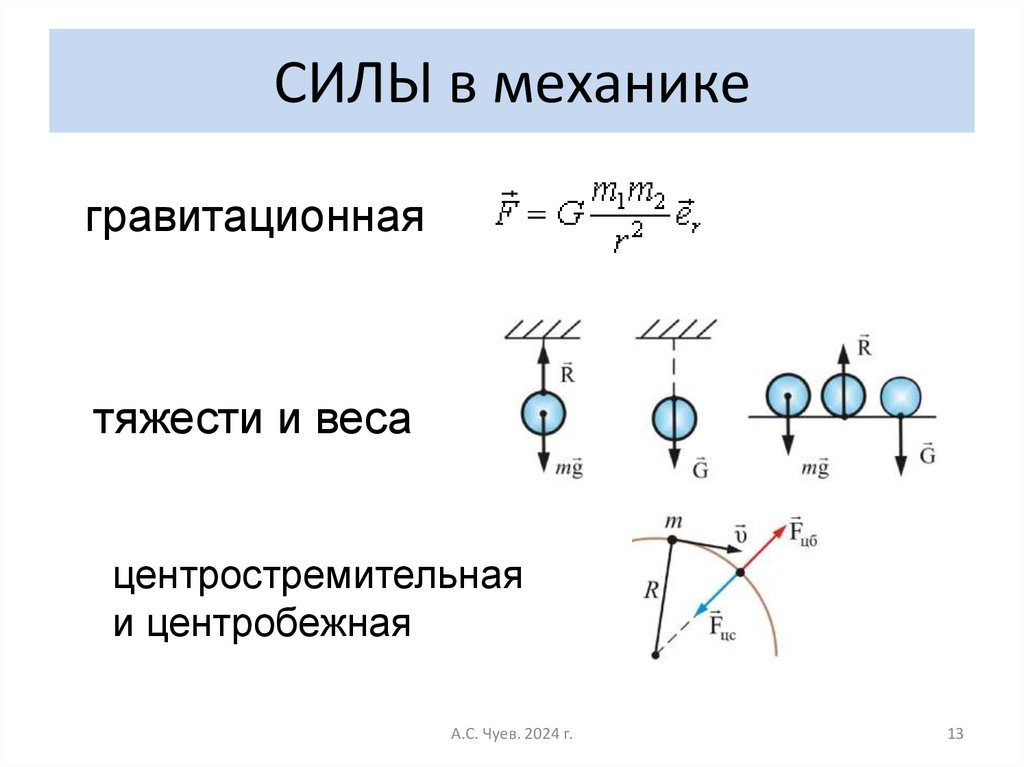
13. СИЛЫ в механике
гравитационнаятяжести и веса
центростремительная
и центробежная
А.С. Чуев. 2024 г.
13
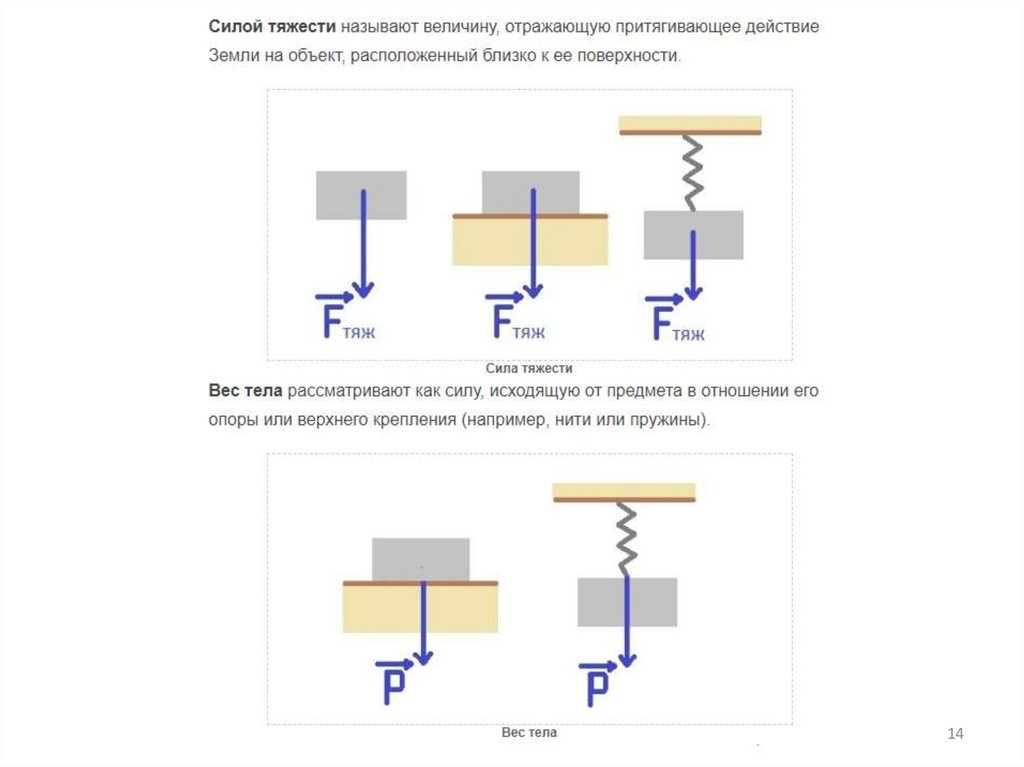
14.
А.С. Чуев. 2024 г.14
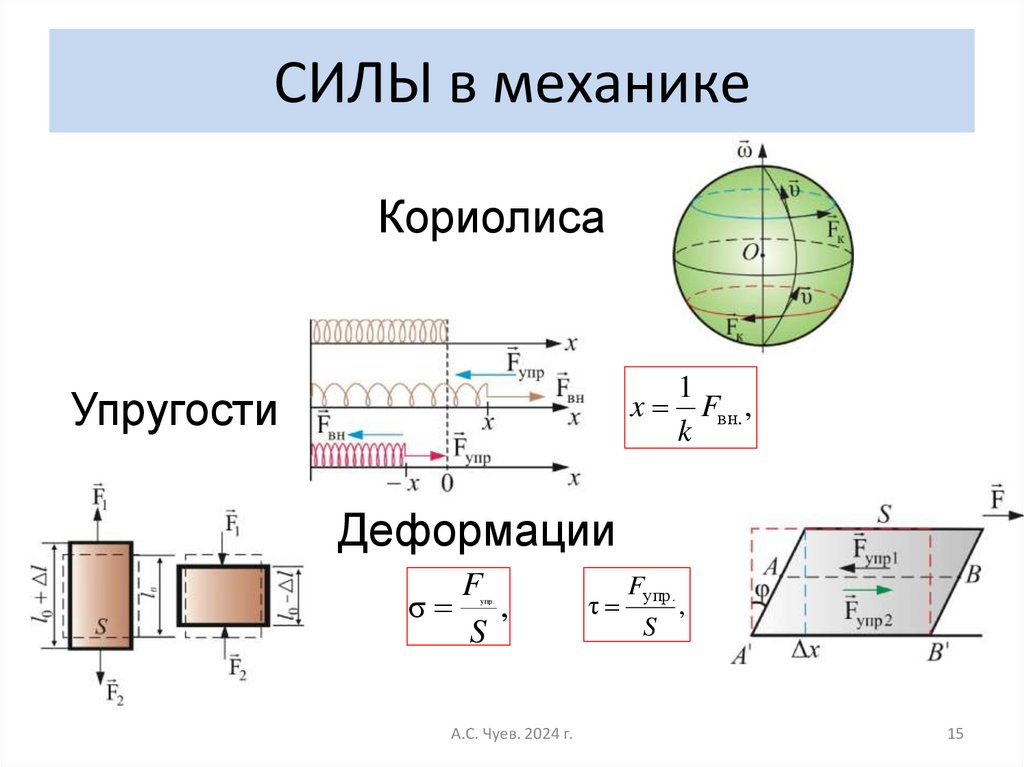
15. СИЛЫ в механике
Кориолиса1
x Fвн. ,
k
Упругости
Деформации
F
σ ,
S
упр.
А.С. Чуев. 2024 г.
τ
Fупр.
S
,
15
16.
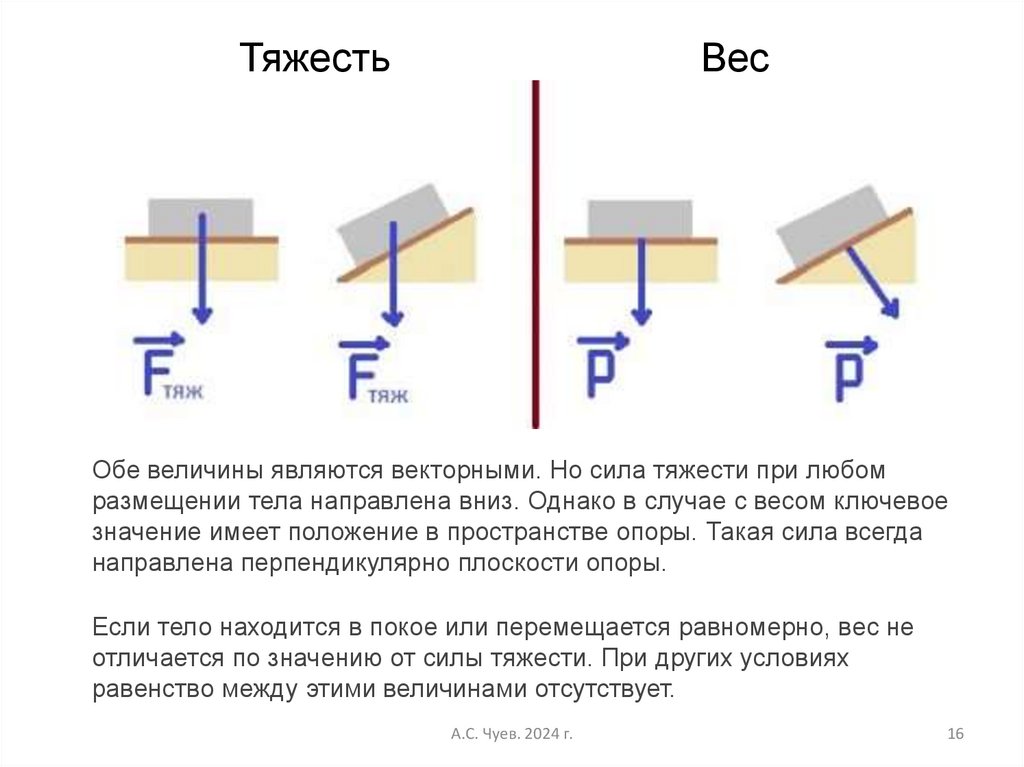
ТяжестьВес
Обе величины являются векторными. Но сила тяжести при любом
размещении тела направлена вниз. Однако в случае с весом ключевое
значение имеет положение в пространстве опоры. Такая сила всегда
направлена перпендикулярно плоскости опоры.
Если тело находится в покое или перемещается равномерно, вес не
отличается по значению от силы тяжести. При других условиях
равенство между этими величинами отсутствует.
А.С. Чуев. 2024 г.
16
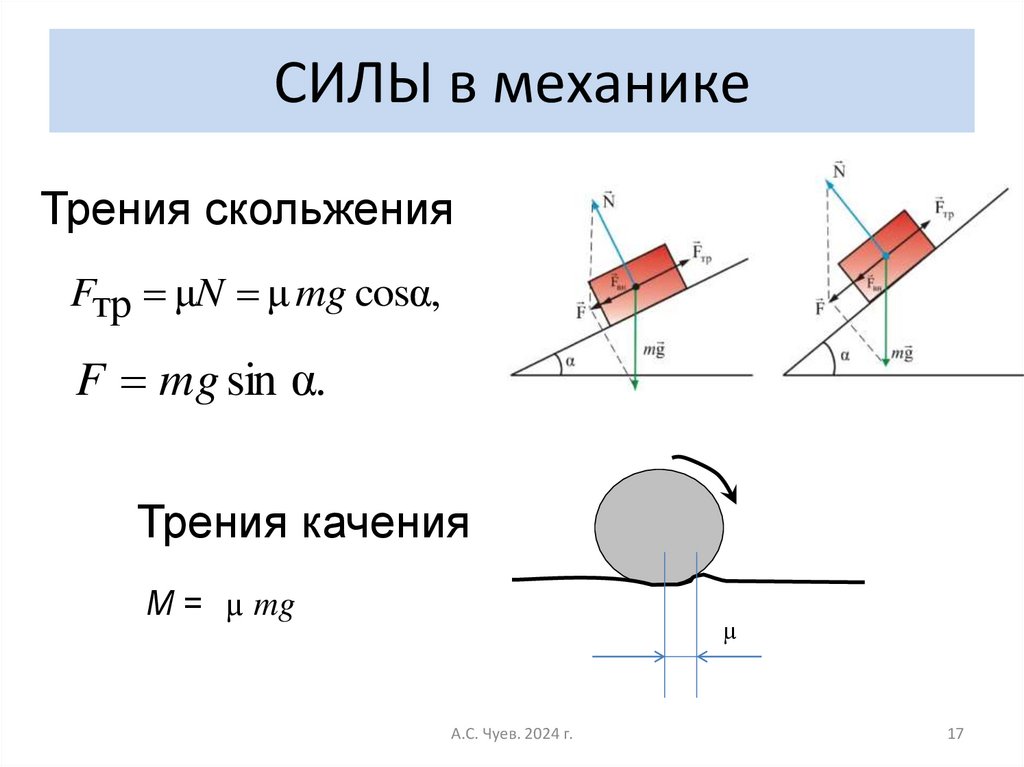
17. СИЛЫ в механике
Трения скольженияFтр μN μ mg cosα,
F mg sin α.
Трения качения
M = µ mg
µ
А.С. Чуев. 2024 г.
17
18.
Трение каченияА.С. Чуев. 2024 г.
18
19.
Соскальзывание частицы с полусферы: h=?h
ФАК
R
А.С. Чуев. 2024 г.
19
20.
Соскальзывание частицы с полусферы: v = ?ФАК
Уравнение для сил:
!
А.С. Чуев. 2024 г.
20
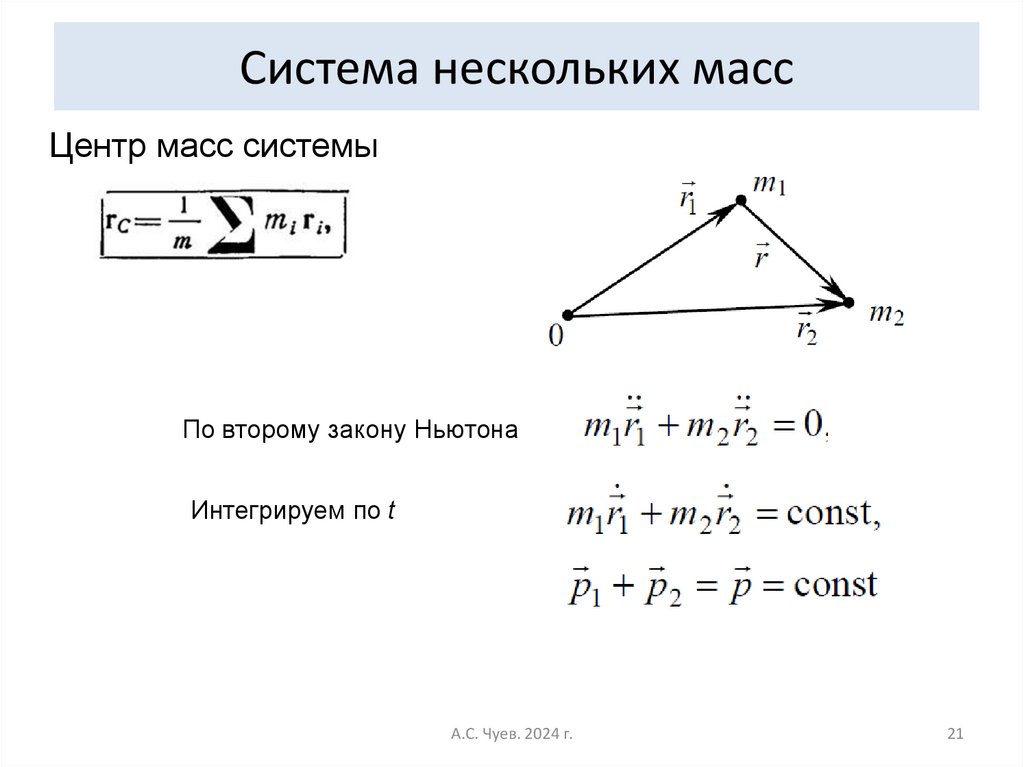
21. Система нескольких масс
Центр масс системыПо второму закону Ньютона
Интегрируем по t
А.С. Чуев. 2024 г.
21
22. Центр масс системы точечных масс
r1 (l1)m1
r1
r2 (l2 )
rC
r2
о
r1 (l1)
m2
m2
(r1 r2)
m1 m 2
rC
r1 (l1) r1 rC
r2 (l2) r2 rC
r2 (l2)
m1
(r2 r1)
m1 m 2
Оба вектора коллиниарны и противоположно направлены, т.о. они лежат
на одной прямой. Модули этих векторов обратно пропорциональны
массам.
А.С. Чуев. 2024 г.
22
23.
Закон сохранения импульса системыА.С. Чуев. 2024 г.
23
24.
А.С. Чуев. 2024 г.24
25.
конспектироватьто же самое и для других внутренних сил.
А.С. Чуев. 2024 г.
25
26.
Скорость системы центра массrC
Уравнение движения ЦМ:
А.С. Чуев. 2024 г.
26
27. Уравнение изменения импульса системы
А.С. Чуев. 2024 г.27
28. Закон сохранения импульса системы
А.С. Чуев. 2024 г.28
29. Пример: человек, движущийся на плоту
А.С. Чуев. 2024 г.29
30.
Ц-система отсчетаУравнение движения ЦМ:
А.С. Чуев. 2024 г.
30
31. Импульсы 2-х частиц в Ц-системе
конспектироватьИмпульсы 2-х частиц в Ц-системе
А.С. Чуев. 2024 г.
31
32. Столкновение двух частиц
конспектироватьСтолкновение двух частиц
соотношение модулей
Линия удара – линия, проходящая через центры масс соударяющихся тел.
А.С. Чуев. 2024 г.
32
33.
Кинетическая энергия в системе ЦМА.С. Чуев. 2024 г.
33
34. Реактивное движение
Формулы знатьУравнение Мещерского:
в нешн dm mdv
F
u
dt
dt
Формула Циолковского:
А.С. Чуев. 2024 г.
34
35.
А.С. Чуев. 2024 г.35
36.
1)А.С. Чуев. 2024 г.
36
37.
При лобовом столкновении двух частиц, имеющих одинаковые модулиимпульсов и скоростей
и
Тогда
А.С. Чуев. 2024 г.
37
38.
Если направление движения тел совпадает с линией удара, тоудар
900 при m1= m2
А.С. Чуев. 2024 г.
38
39.
Для АУУ, решивсистему уравнений
относительно скоростей, получим:
Обозначим:
U 1 v 1
U 2 v 2
2m2 v 2 (m1 m2 )v1
v1
;
m1 m2
2m1 v1 (m2 m1 )v 2
v 2
.
m1 m2
А.С. Чуев. 2024 г.
39
40.
Абсолютно упругий удар шарао массивную стенку.
Стенку можно рассматривать как неподвижный шар
с v 2 0 и массой m2
Разделив числитель и знаменатель предшествующей
формулы на m2 и пренебрегая m1 / m2 , получим
m1
2 v 2
1 v1
m2
2v 2 v1
v1
,
m1
1
1
m2
при v 2 0 и ударе в нормаль
v'1 v1
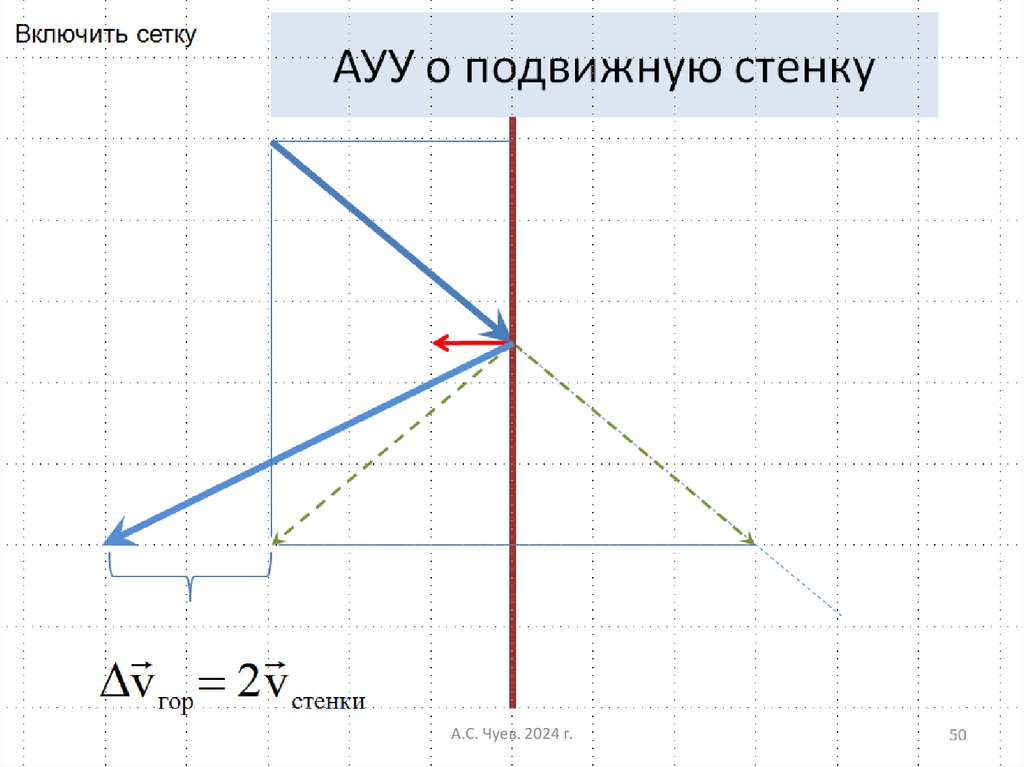
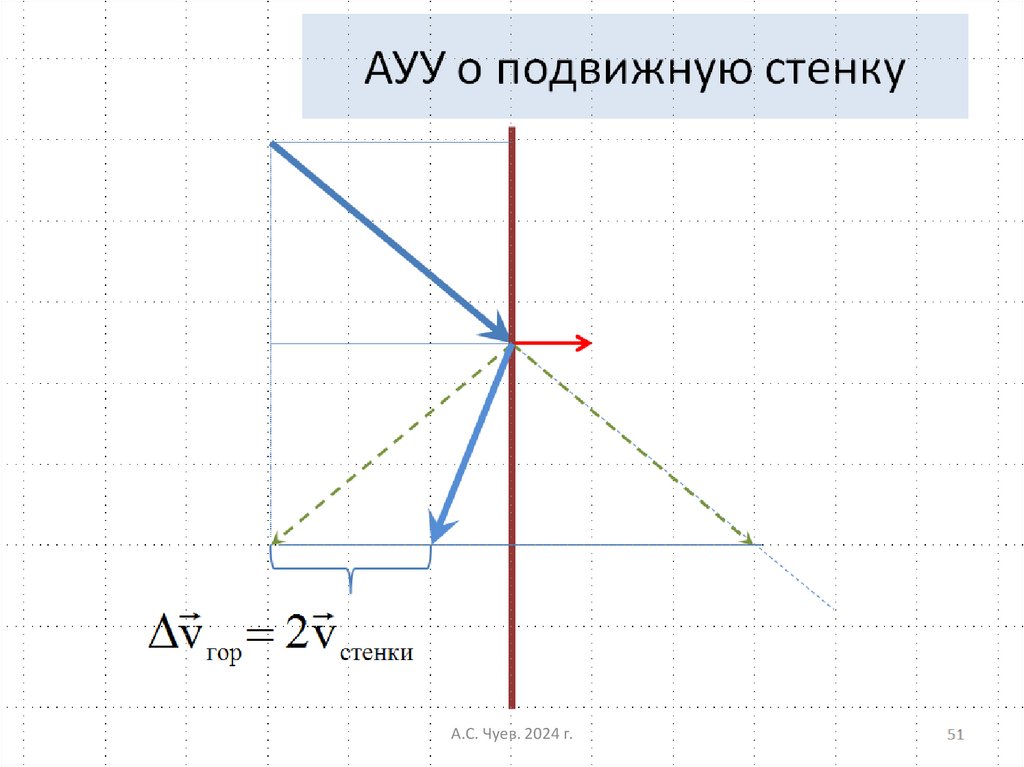
При АУУ и отскоке шара от движущейся стенки, горизонтальная проекция
скорости изменяется на две скорости
А.С. Чуев.стенки
2024 г.
40
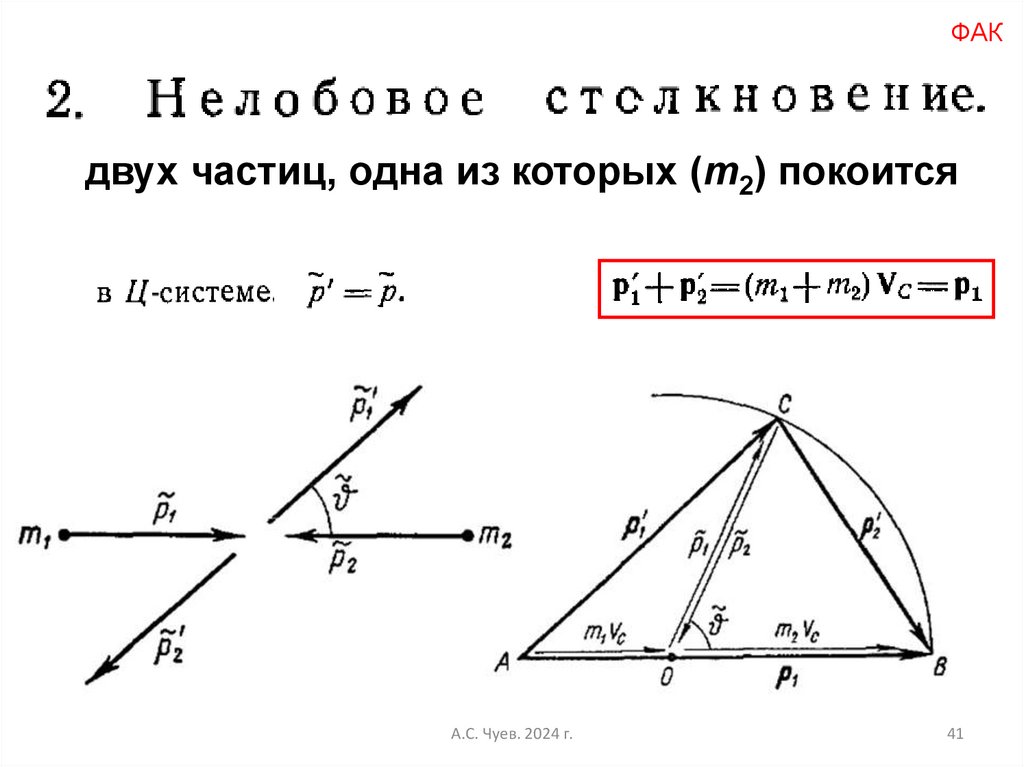
41.
ФАКдвух частиц, одна из которых (m2) покоится
А.С. Чуев. 2024 г.
41
42.
ФАКВывод конечной формулы:
А.С. Чуев. 2024 г.
42
43.
ФАКА.С. Чуев. 2024 г.
43
44.
Адрес ДЗ для 2 семестраhttp://fn.bmstu.ru/learning-work-fs4/semester-2-fs-4
А.С. Чуев. 2024 г.
44
45.
А.С. Чуев. 2024 г.45
46.
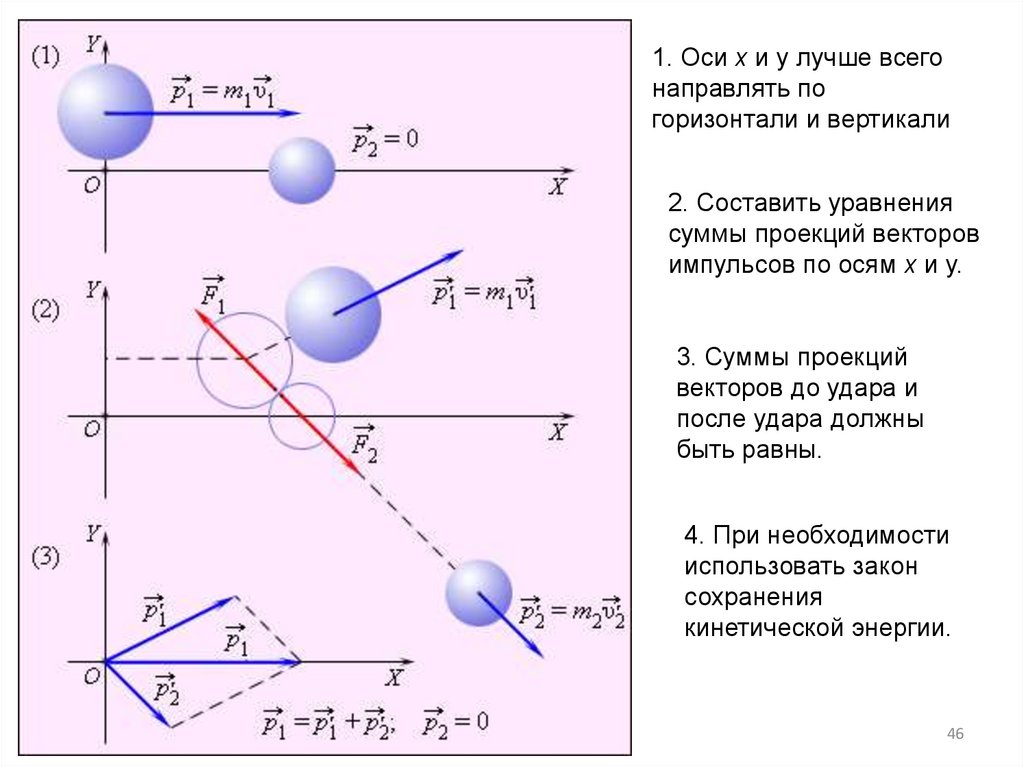
1. Оси х и y лучше всегонаправлять по
горизонтали и вертикали
2. Составить уравнения
суммы проекций векторов
импульсов по осям х и y.
3. Суммы проекций
векторов до удара и
после удара должны
быть равны.
4. При необходимости
использовать закон
сохранения
кинетической энергии.
А.С. Чуев. 2024 г.
46
47.
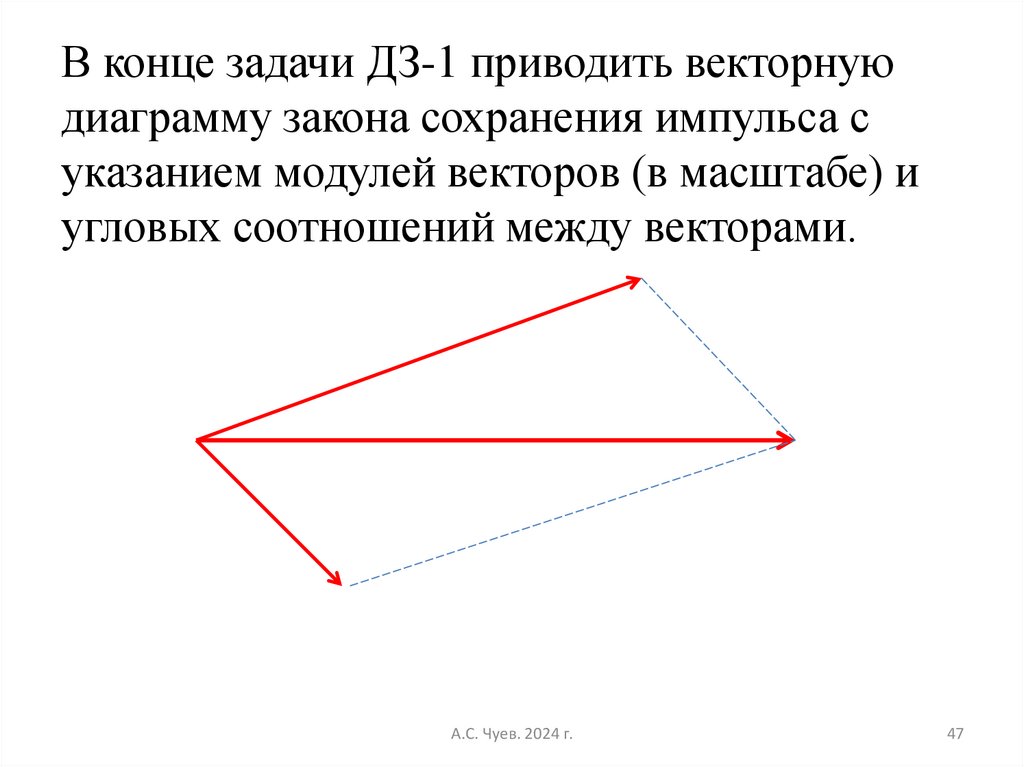
В конце задачи ДЗ-1 приводить векторнуюдиаграмму закона сохранения импульса с
указанием модулей векторов (в масштабе) и
угловых соотношений между векторами.
А.С. Чуев. 2024 г.
47
48.
Абсолютно упругий удар шара омассивную стенку – ДЗ-1
А.С. Чуев. 2024 г.
48
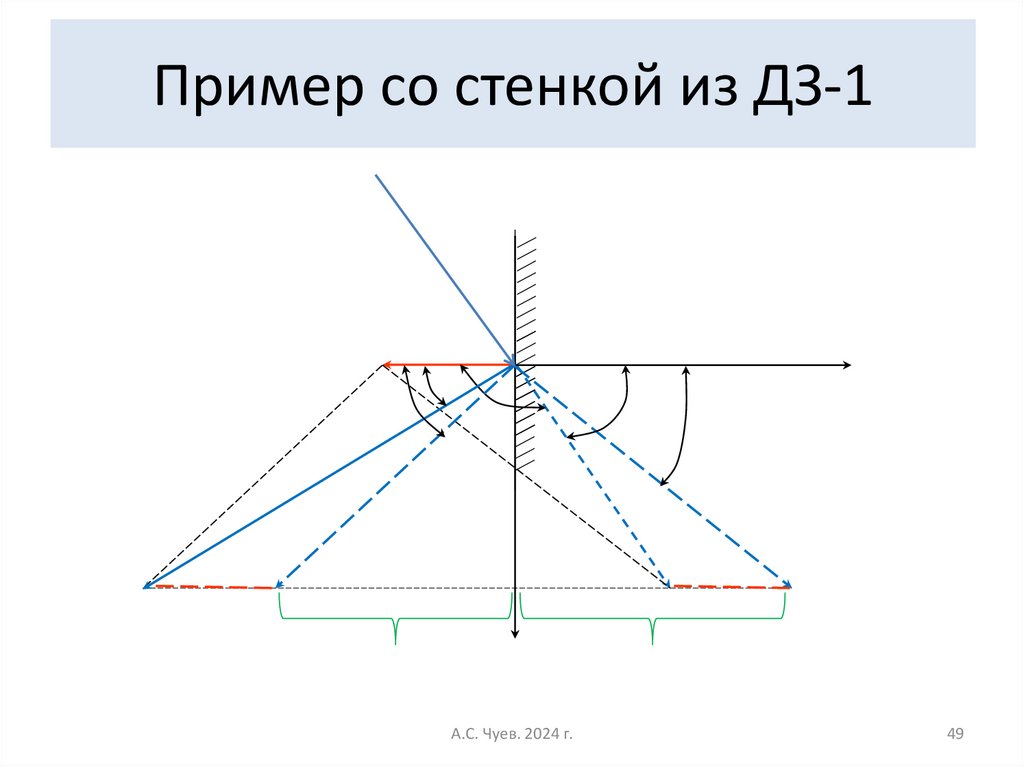
49. Пример со стенкой из ДЗ-1
А.С. Чуев. 2024 г.49
50.
А.С. Чуев. 2024 г.50
51.
А.С. Чуев. 2024 г.51
52.
Далее факультативный материалА.С. Чуев. 2024 г.
52
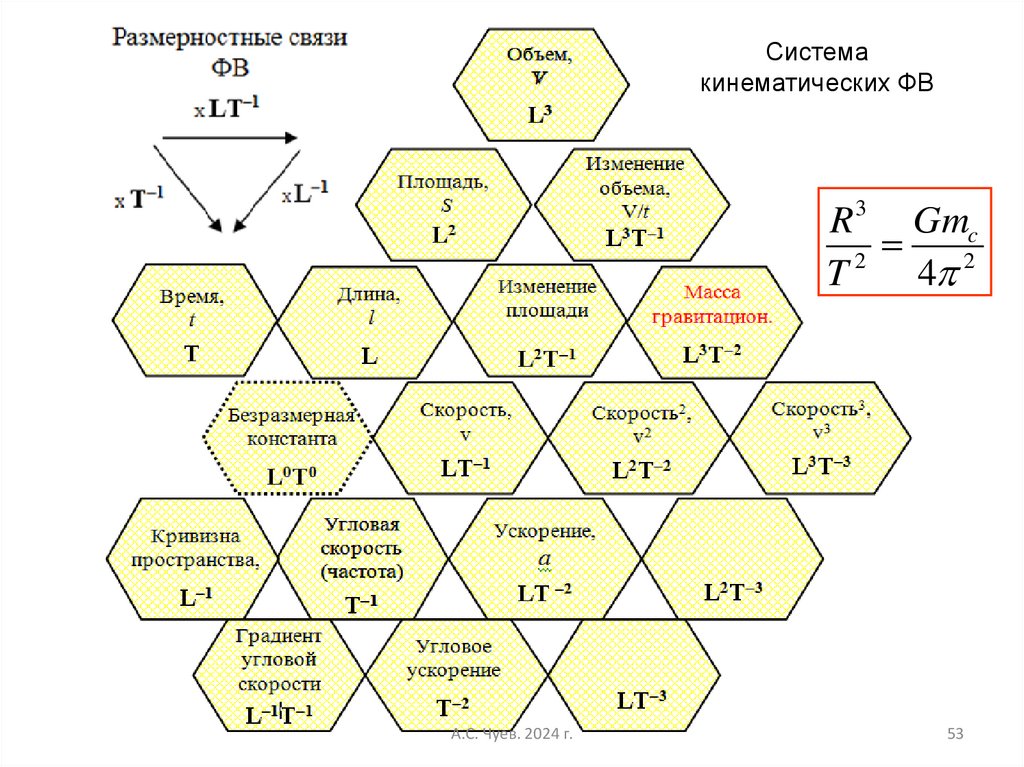
53.
Системакинематических ФВ
R 3 Gmc
2
T
4 2
А.С. Чуев. 2024 г.
53
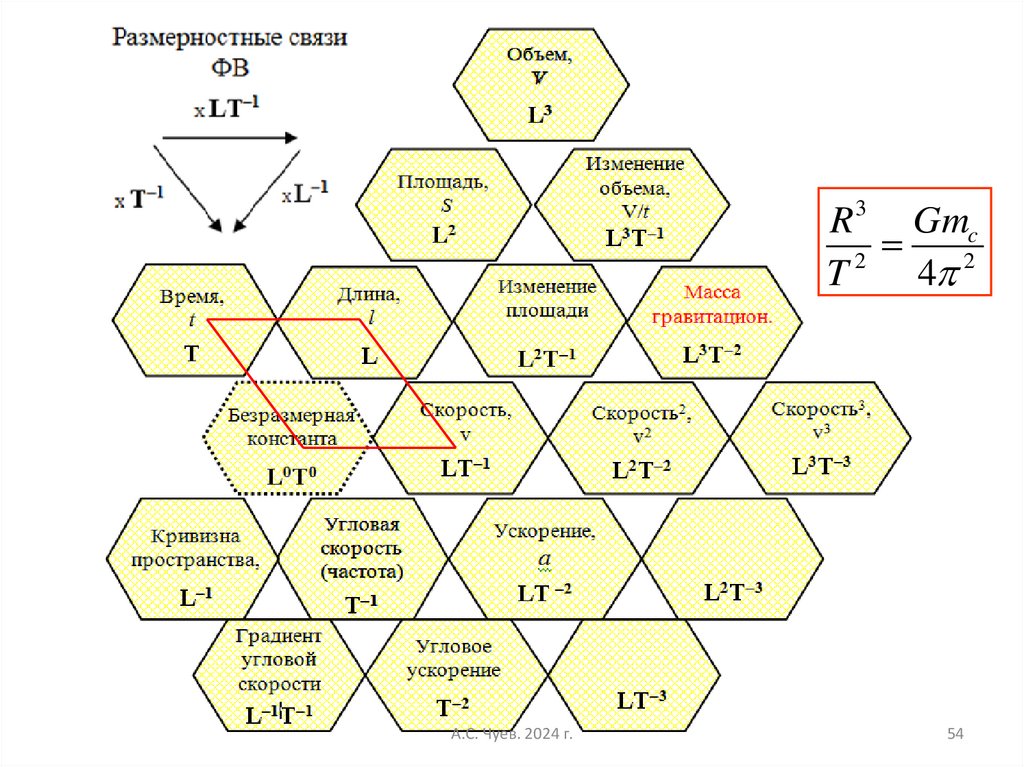
54.
R 3 Gmc2
T
4 2
А.С. Чуев. 2024 г.
54
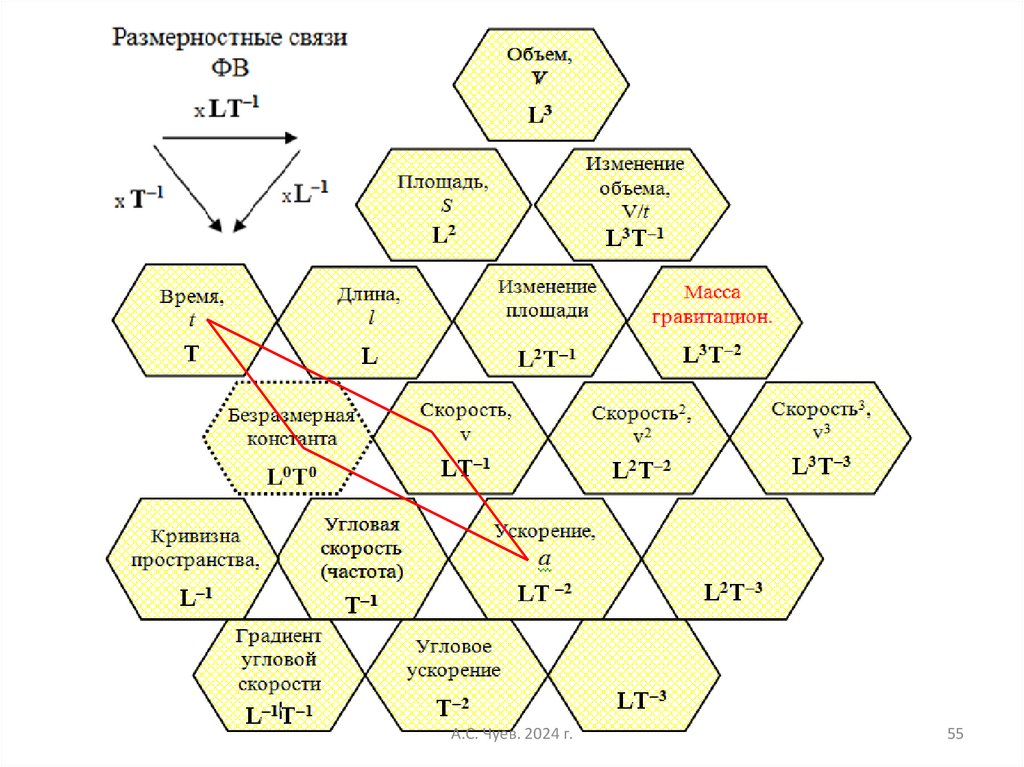
55.
А.С. Чуев. 2024 г.55
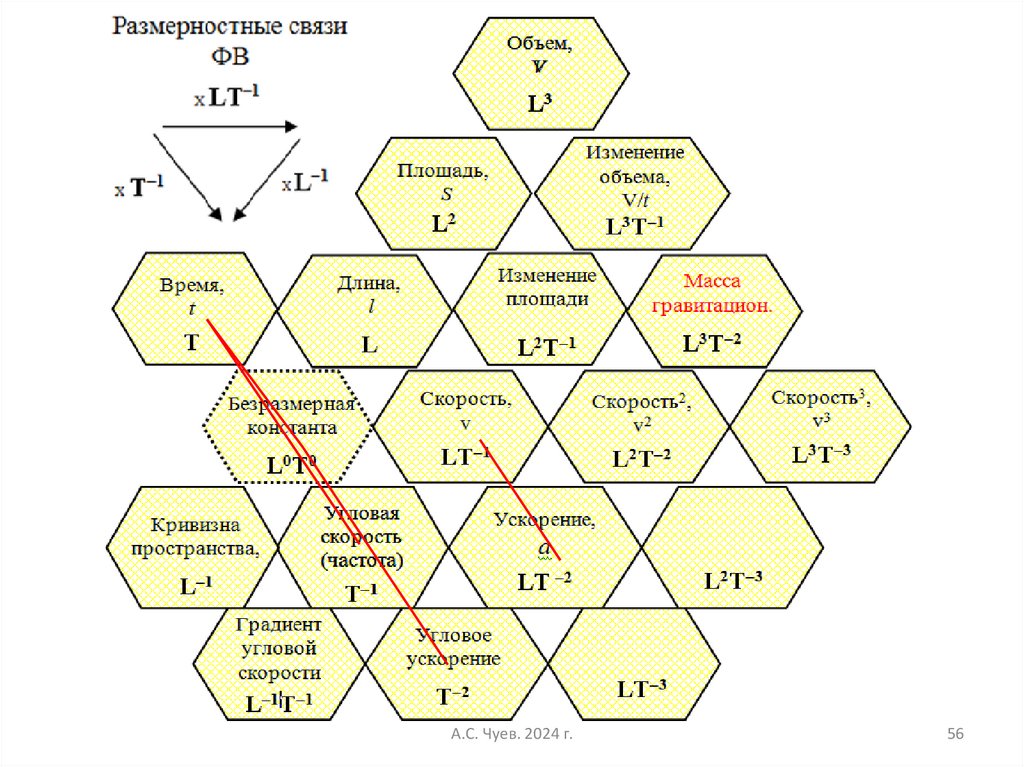
56.
А.С. Чуев. 2024 г.56
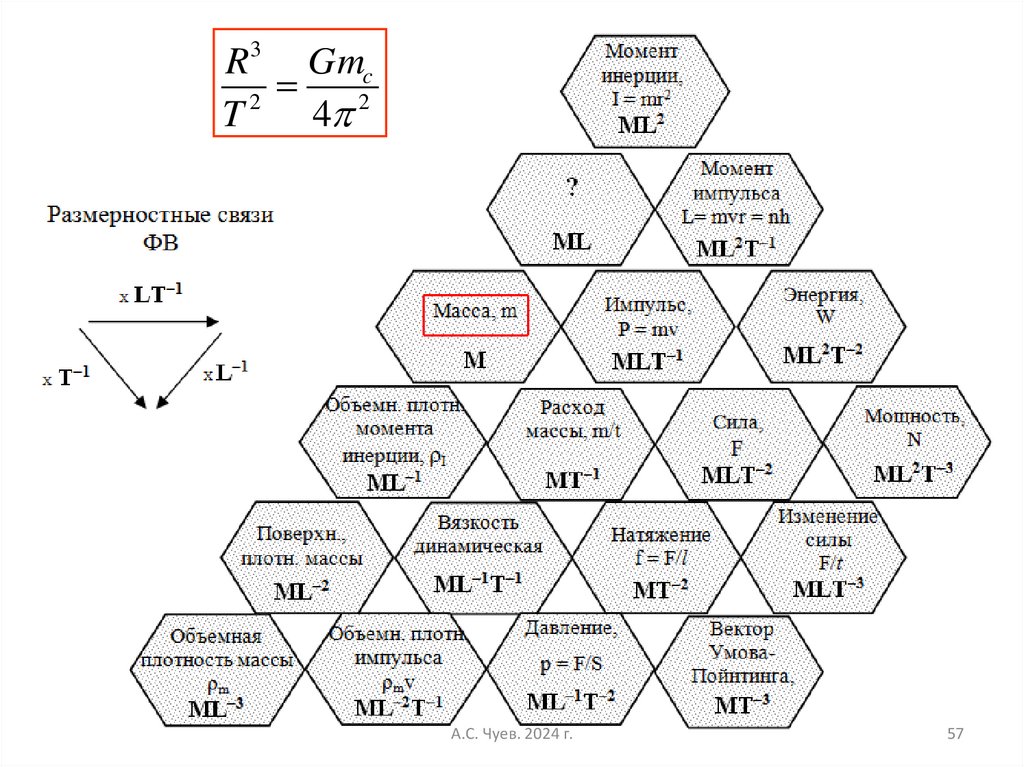
57.
R 3 Gmc2
T
4 2
А.С. Чуев. 2024 г.
57
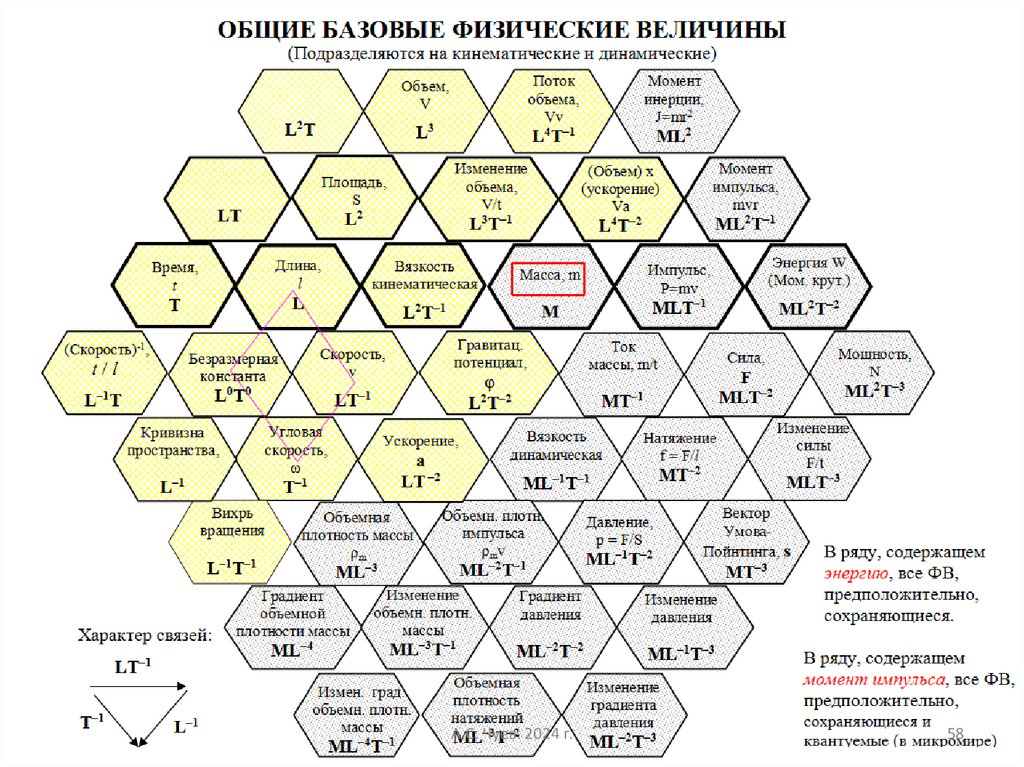
58.
А.С. Чуев. 2024 г.58
59.
А.С. Чуев. 2024 г.59
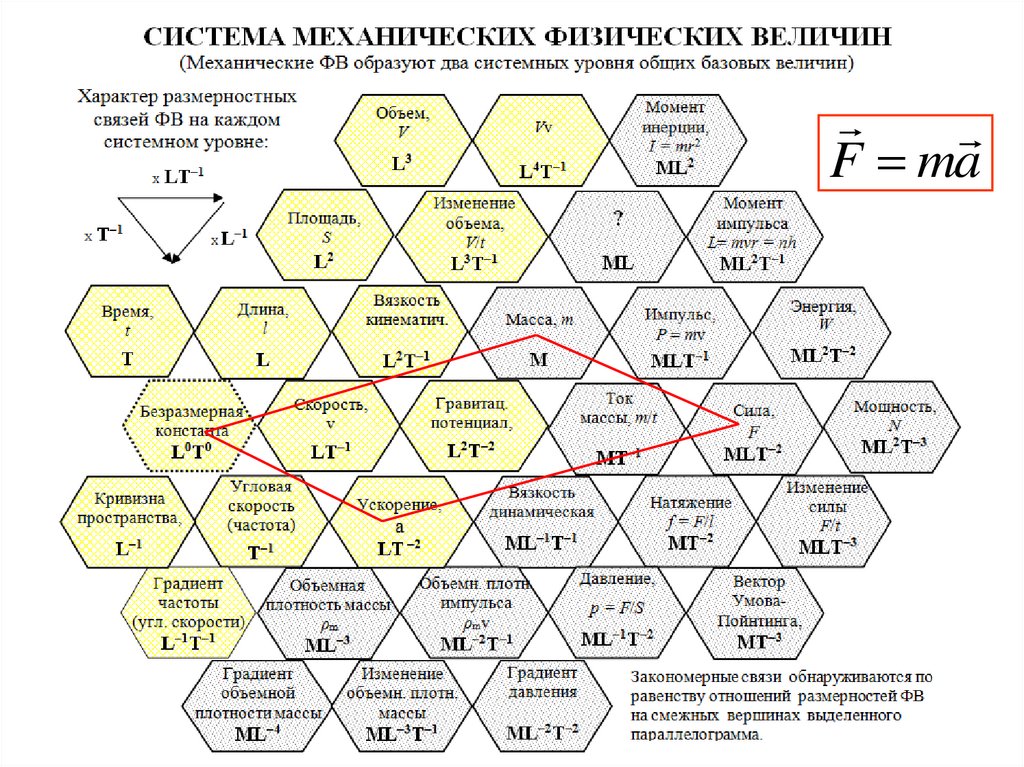
60.
F maА.С. Чуев. 2024 г.
60
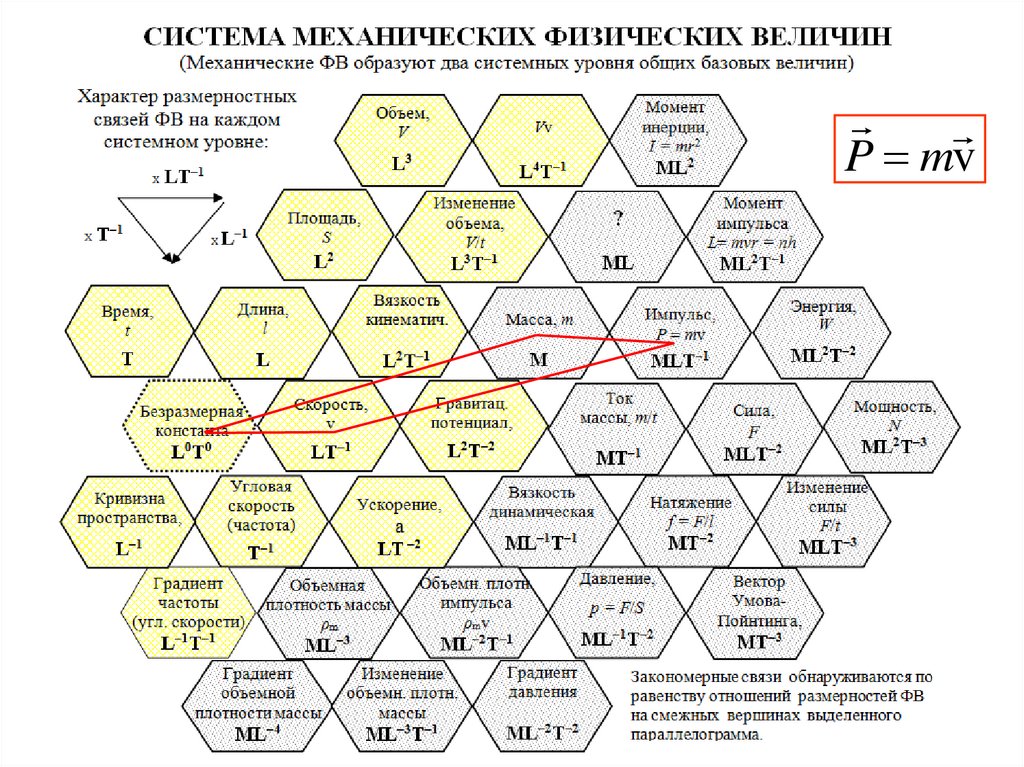
61.
P mvА.С. Чуев. 2024 г.
61
62.
dPF
dt
А.С. Чуев. 2024 г.
62
63.
Конец лекции 2-2024А.С. Чуев. 2024 г.
63










































 Физика
Физика








