Похожие презентации:
Пирамида и её элементы. Правильная пирамида
1.
2.
Пирамидой называетсямногогранник, который состоит
из плоского многоугольника –
основания пирамиды, точки, не
лежащей в плоскости основания,
- вершины пирамиды и всех
отрезков, соединяющих вершину
с точками основания.
3.
S – ВЕРШИНА ПИРАМИДЫABCDE – ОСНОВАНИЕ ПИРАМИДЫ
S
Вершина
пирамиды
Основание
пирамиды
B
A
C
E
D
4.
Отрезки, соединяющие вершину пирамиды свершинами основания, называются боковыми
рёбрами.
SA, SB, SC, SD, SE - боковые рёбра пирамиды SABCDЕ.
S
Боковые
рёбра
пирамиды
B
A
C
E
D
5.
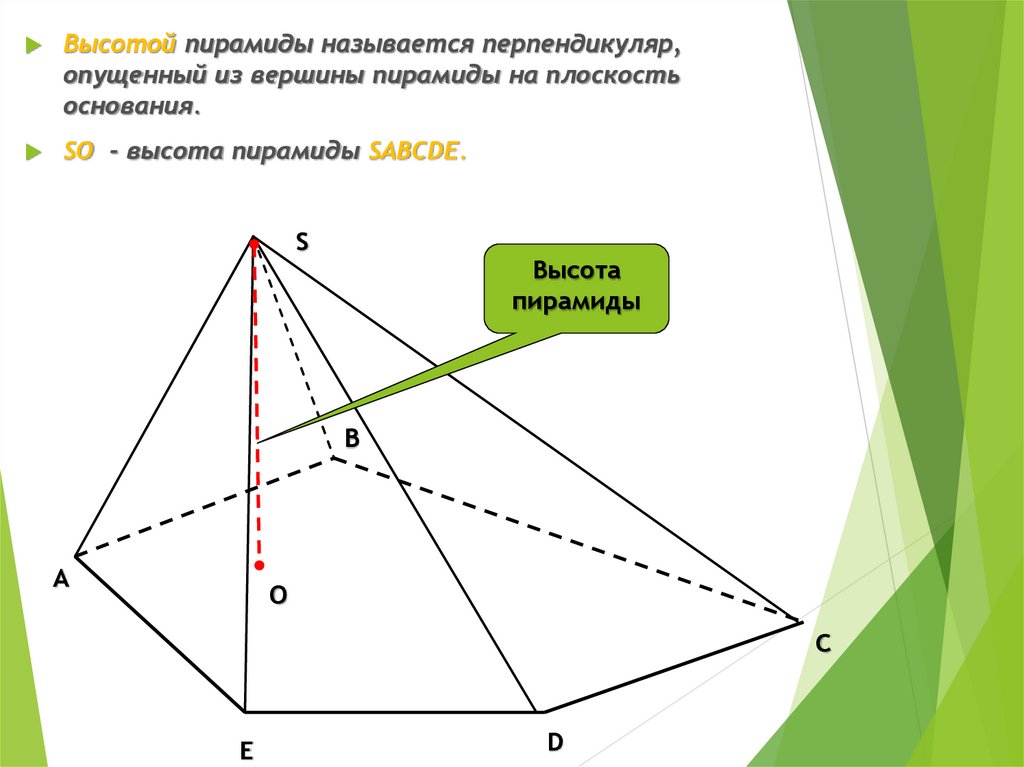
Высотой пирамиды называется перпендикуляр,опущенный из вершины пирамиды на плоскость
основания.
SО - высота пирамиды SABCDЕ.
S
Высота
пирамиды
B
A
О
C
E
D
6.
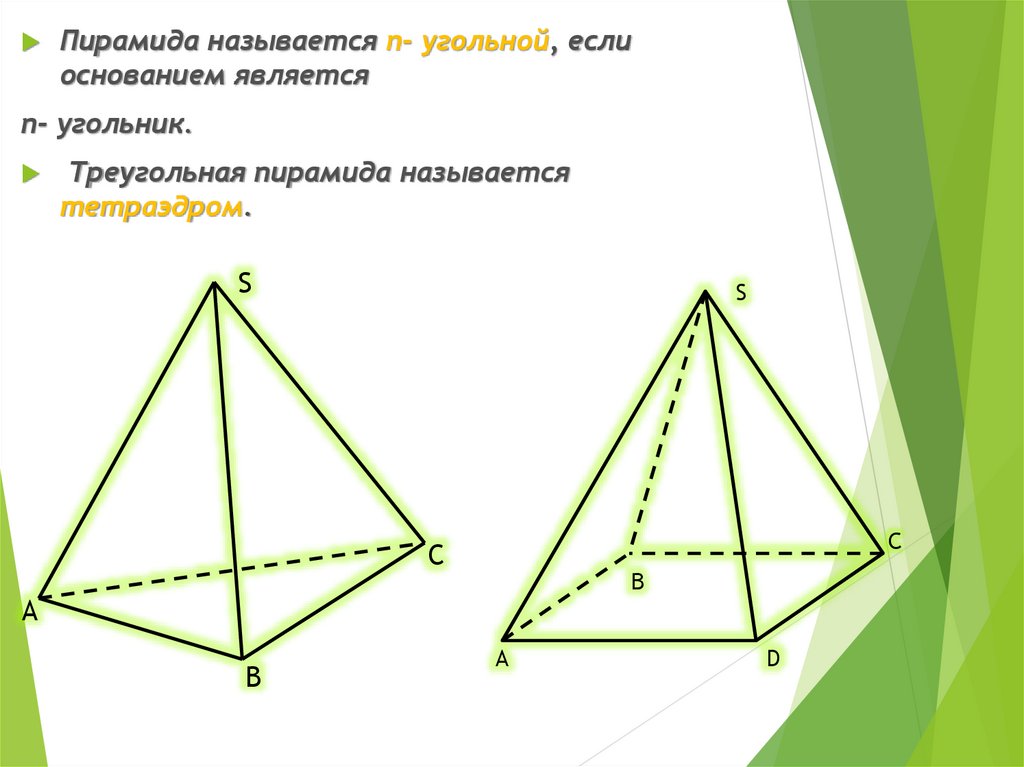
Пирамида называется n- угольной, еслиоснованием является
n- угольник.
Треугольная пирамида называется
тетраэдром.
S
S
C
C
B
A
B
A
D
7.
Пирамида называется правильной, если еёоснованием является правильный
многоугольник, а основание высоты совпадает с
центром этого многоугольника.
8.
Осью правильной пирамиды называетсяпрямая, содержащая её высоту.
Ось
пирамиды
9.
Высота боковой грани правильнойпирамиды, проведённая из её вершины,
называется апофемой.
SF – апофема пирамиды SABCD.
S
Апофема
пирамиды
B
С
F
D
10.
11.
Рассмотрим пирамиду PA1A2…An и проведёмсекущую плоскость ß, параллельную
плоскость и α основания пирамиды и
пересекающую боковые рёбра в точках
В1,В2…Вn.
Плоскость ß разбивает пирамиду на 2
многогранника.
A1A2…AnВ1В2…Вn –
.
A1В1,…AnВn – боковые рёбра.
A1В1В2A2… - боковые грани.
A1A2…An , В1В2…Вn – основания
усечённой пирамиды
12.
Плоскость, параллельная основанию пирамидыи пересекающая её, отсекает подобную
пирамиду.
13.
Усечённая пирамида называется, если она получена сечением
правильной пирамиды плоскостью,
параллельной основанию.
14.
15.
Боковой поверхностью пирамидыназывается сумма площадей её боковых
граней.
16.
Площадь боковой поверхностиправильной пирамиды равна
произведению полупериметра
основания на апофему:
p – периметр основания;
l - апофема пирамиды
l
17.
Площадь боковой поверхности правильнойусечённой пирамиды равна произведению
полусуммы периметров оснований на
апофему:
p1 и p2 – периметры оснований;
l - апофема пирамиды.
18.
19.
Площадь полной поверхности правильнойпирамиды равна сумме площади боковой
поверхности и площади основания:
20.
21.
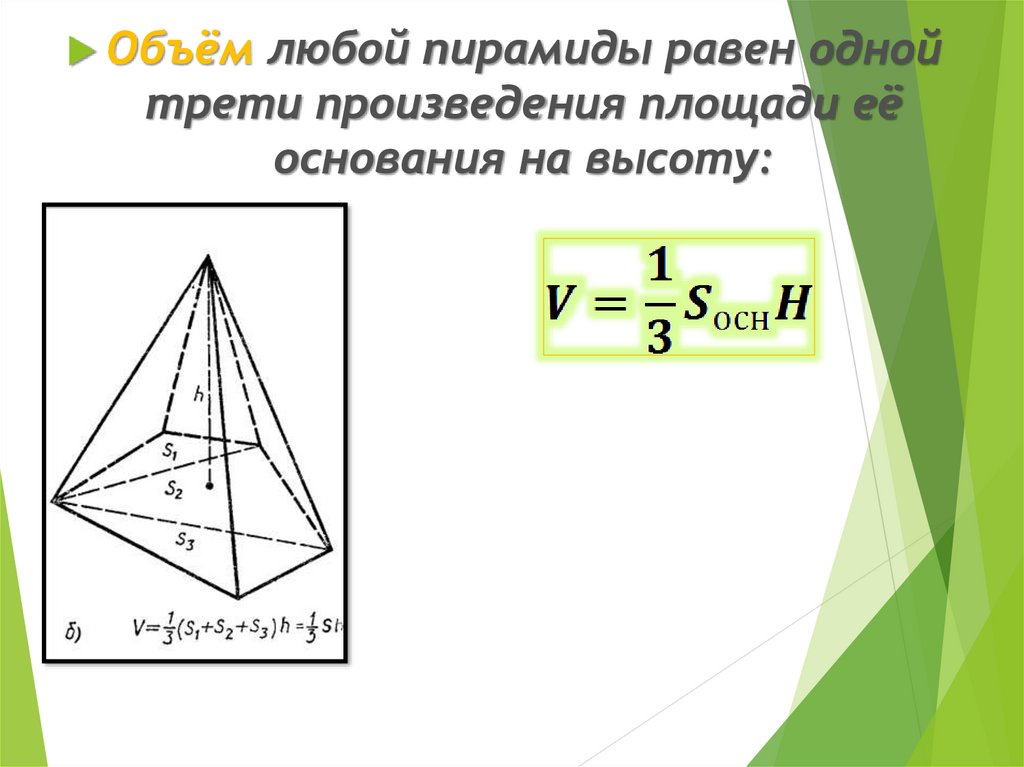
Объёмлюбой пирамиды равен одной
трети произведения площади её
основания на высоту:
22.
23.
Объёмусечённой пирамиды с
площадями оснований Q1 и Q2 и
высотой H :
Q1
Q2
24.
Найдите объём тетраэдра(правильная треугольная
пирамида), если его
высота и сторона
основания равна 3 дм.
P
3 дм
3 дм
A
B
3 дм
H
3 дм
C
25.
Основание пирамиды –прямоугольник со
сторонами 9 м и 12 м; все
боковые рёбра равны 12,5
м. Найдите объём
пирамиды.
F
12,5 м
B
C
9м
Н
A
12 м
D






















 Математика
Математика








