Похожие презентации:
Основы термодинамики. Первое начало термодинамики. Работа газа при изменении объема. Теплоемкость идеального газа
11.
Основы термодинамики 11.1 Первое начало термодинамики При термодинамическом описании свойств макросистем используют закономерности, наблюдающиеся в опытных данных.
Первый закон термодинамики представляет собой закон сохранения энергии, обобщенный на тепловые процессы.
В этот закон входят3 величины : 1) внутренняя энергия макросистемыU 2) работаA 3) теплотаQ Рассмотрим эти величины подробно.
11.1 Первое начало термодинамики При термодинамическом описании свойств макросистем используют закономерности, наблюдающиеся в опытных данных.
Первый закон термодинамики представляет собой закон сохранения энергии, обобщенный на тепловые процессы.
В этот закон входят3 величины :1) внутренняя энергия макросистемыU2) работаA3) теплотаQ Рассмотрим эти величины подробно.
Внутренняя энергия макросистемыU состоит из двух частей: 1) кинетической энергии хаотического движения молекул в системе координат, связанной с центром масс системы 2) потенциальной энергии взаимодействия между молекулами системы При этом кинетическая энергия системы как целого и ее потенциальная энергия во внешнем поле во внутреннюю энергиюU не входят.
Если система состоит из нескольких тел, то ее внутренняя энергия равна сумме внутренних энергий тел и потенциальных энергий взаимодействия между ними.
Внутренняя энергия макросистемыU состоит из двух частей:1) кинетической энергии хаотического движения молекул в системе координат, связанной с центром масс системы2) потенциальной энергии взаимодействия между молекулами системы При этом кинетическая энергия системы как целого и ее потенциальная энергия во внешнем поле во внутреннюю энергиюU не входят.
Если система состоит из нескольких тел, то ее внутренняя энергия равна сумме внутренних энергий тел и потенциальных энергий взаимодействия между ними.
Разобьем макросистему на достаточно большие части.
Поскольку межмолекулярные силы короткодействующие, то потенциальной энергией взаимодействия между частями на границах можно пренебречь.
Поэтому внутренняя энергия всей системы равна сумме внутренних энергий ее частей: U = U1+ U2 + … + UN Об этом свойстве внутренней энергииU говорят, что она является аддитивной величиной.
Разобьем макросистему на достаточно большие части.
Поскольку межмолекулярные силы короткодействующие, то потенциальной энергией взаимодействия между частями на границах можно пренебречь.
Поэтому внутренняя энергия всей системы равна сумме внутренних энергий ее частей: U = U1+ U2 + … + UN Об этом свойстве внутренней энергииU говорят, что она является аддитивной величиной.1234567 Внутренняя энергияU обладает еще одним свойством – она является функцией состояния.
Это значит, что величина внутренней энергииU не зависит от того, каким способом макросистема была переведена в данное состояние.
Поэтому изменение внутренней энергииU при переходе системы из одного состояния в другое состояние равно разности внутренних энергий в конечном и начальном состояниях.
Внутренняя энергияU обладает еще одним свойством – она является функцией состояния.
Это значит, что величина внутренней энергииU не зависит от того, каким способом макросистема была переведена в данное состояние.
Поэтому изменение внутренней энергииU при переходе системы из одного состояния в другое состояние равно разности внутренних энергий в конечном и начальном состояниях.
Внутреннюю энергию макросистемыU можно изменить двумя способами 1) совершив над ней работуA 2) сообщив ей некоторое количество теплотыQ Внутреннюю энергию макросистемыU можно изменить двумя способами1) совершив над ней работуA2) сообщив ей некоторое количество теплотыQ При совершении работыA над макросистемой происходит перемещение внешних к ней тел.
Например, при движении поршня в цилиндре с газом, поршень совершает работуA над газом и изменяет его внутреннюю энергию.
Газ в свою очередь тоже совершает работу над поршнем, обозначим ее черезA.
Из3 - го закона Ньютона следует A = - A Далее работу, совершаемую макросистемой над внешними телами будем обозначать черезA .
При совершении работыA над макросистемой происходит перемещение внешних к ней тел.
Например, при движении поршня в цилиндре с газом, поршень совершает работуA над газом и изменяет его внутреннюю энергию.
Газ в свою очередь тоже совершает работу над поршнем, обозначим ее черезA.
Из3 - го закона Ньютона следуетA = - A Далее работу, совершаемую макросистемой над внешними телами будем обозначать черезA .
С другой стороны передача теплотыQ не связана с перемещением внешних тел.
Передача теплоты происходит при контакте внешних тел с макросистемой.
В этом случае изменение внутренней энергии системыU связано с работой молекул более нагретого тела над молекулами менее нагретого тела.
С другой стороны передача теплотыQ не связана с перемещением внешних тел.
Передача теплоты происходит при контакте внешних тел с макросистемой.
В этом случае изменение внутренней энергии системыU связано с работой молекул более нагретого тела над молекулами менее нагретого тела.
ТеплотаQ равна энергии, переданной системе внешними телами посредством таких микроскопических процессов.
Из 3 - го закона Ньютона следует, что макросистема в свою очередь передает внешним телам количество теплотыQ = -Q ЕслиQ >0 , то тепло передается от внешней среды макросистеме.
ЕслиQ <0 , то тепло отводится от макросистемы, то есть передается от нее внешней среде.
Внутренняя энергия системы может также меняться при облучении электромагнитными волнами.
При этом поглощенная энергия фотонов переходит в энергию возбужденных состояний молекул макросистемы.
ТеплотаQ равна энергии, переданной системе внешними телами посредством таких микроскопических процессов.
Из 3 - го закона Ньютона следует, что макросистема в свою очередь передает внешним телам количество теплотыQ = -Q ЕслиQ >0 , то тепло передается от внешней среды макросистеме.
ЕслиQ <0 , то тепло отводится от макросистемы, то есть передается от нее внешней среде.
Внутренняя энергия системы может также меняться при облучении электромагнитными волнами.
При этом поглощенная энергия фотонов переходит в энергию возбужденных состояний молекул макросистемы.
Из закона сохранения энергии следует , что изменение внутренней энергии системыU при ее переходе из начального состояния1 в конечное состояние2 равно сумме совершенной над системой работы внешних телA и переданного системе теплаQ , то естьU =U2 - U1 =A +Q ПосколькуA = -A , то (11.1.1) Эта формула выражает собой первое начало термодинамики: Количество теплотыQ , переданное системе, идет на приращение ее внутренней энергииU и на совершение работыA над внешними телами.
Из закона сохранения энергии следует , что изменение внутренней энергии системыU при ее переходе из начального состояния1 в конечное состояние2 равно сумме совершенной над системой работы внешних телAи переданного системе теплаQ, то естьU =U2 - U1 =A +Q ПосколькуA = -A, то (11.1.1) Эта формула выражает собой первое начало термодинамики: Количество теплотыQ, переданное системе, идет на приращение ее внутренней энергииU и на совершение работыA над внешними телами. Q=U+A Если U > 0 , то совершенная системой работа меньше полученного количества теплоты, то есть Q > A и наоборот.
Для элементарных процессов, когда два состояния системы близки друг к другу, формула (11.1.1) принимает вид (11.1.2) Штрихи означают, что изменение теплотыdQ и совершенная работаdA зависят от способа перехода системы из одного состояния в другое состояние.
Значит в отличие от внутренней энергииU теплотаQ и работаA не являются функциями состояния.
Поэтому величиныdQ иdА не являются полными дифференциалами , тогда какdU - полный дифференциал.
Если U > 0, то совершенная системой работа меньше полученного количества теплоты, то есть Q > Aи наоборот.
Для элементарных процессов, когда два состояния системы близки друг к другу, формула (11.1.1) принимает вид (11.1.2) Штрихи означают, что изменение теплотыdQ и совершенная работаdA зависят от способа перехода системы из одного состояния в другое состояние.
Значит в отличие от внутренней энергииU теплотаQ и работаA не являются функциями состояния.
Поэтому величиныdQ иdА не являются полными дифференциалами , тогда какdU - полный дифференциал.
d'Q=dU+d'A Пусть макросистема совершает процесс, в ходе которого она периодически возвращается в исходное состояние, тогда ее внутренняя энергияU не будет меняться в таком процессе U = 0 Согласно (11.1.1) в этом случае работаА , совершаемая системой будет равна переданной ей теплотеQ А = Q Следовательно: невозможен периодически действующий двигатель, совершающий работуА большую, чем переданная ему тепловая энергияQ.
Вечный двигатель первого рода невозможен.
Пусть макросистема совершает процесс, в ходе которого она периодически возвращается в исходное состояние, тогда ее внутренняя энергияU не будет меняться в таком процессе U = 0 Согласно (11.1.1) в этом случае работаА , совершаемая системой будет равна переданной ей теплотеQА=Q Следовательно: невозможен периодически действующий двигатель, совершающий работуА большую, чем переданная ему тепловая энергияQ.
Вечный двигатель первого рода невозможен.
ТеплотаQ измеряется в тех же единицах, что энергияU и работаА , то есть в джоулях.
Раньше применялась единица количества теплоты калория.
Калория и джоуль связаны соотношениями 1 кал = 4.18 Дж 1 Дж = 0.24 кал ТеплотаQ измеряется в тех же единицах, что энергияU и работаА , то есть в джоулях.
Раньше применялась единица количества теплоты калория.
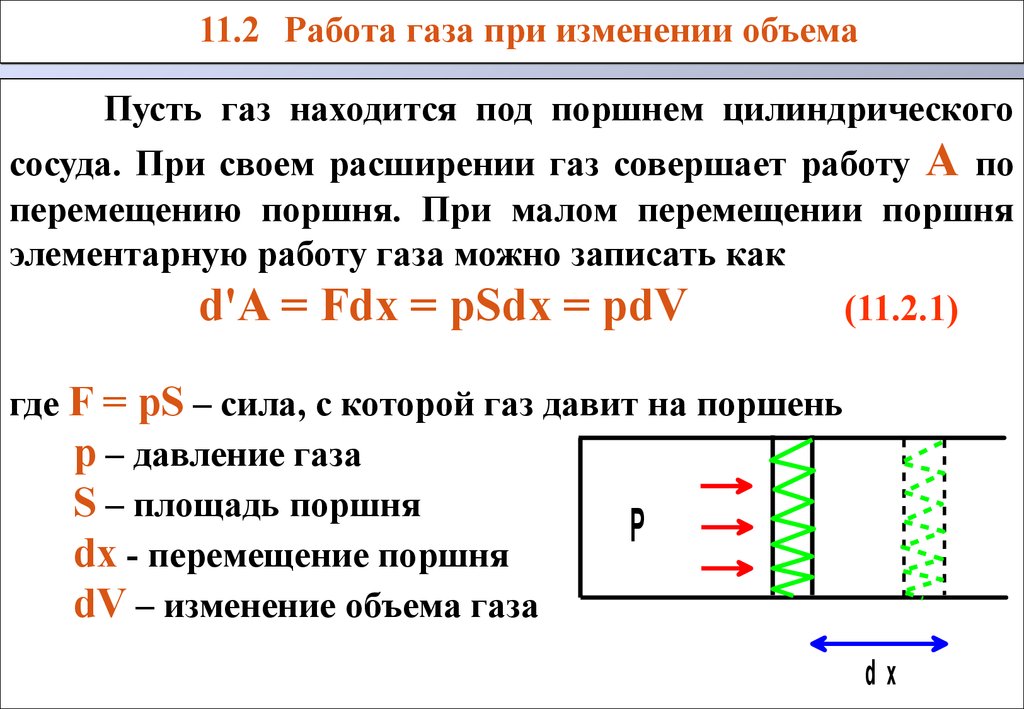
Калория и джоуль связаны соотношениями 1 кал = 4.18 Дж 1 Дж = 0.24 кал Пусть газ находится под поршнем цилиндрического сосуда.
При своем расширении газ совершает работуA по перемещению поршня.
При малом перемещении поршня элементарную работу газа можно записать как d'A = Fdx = pSdx = pdV (11.2.1) где F = pS – сила, с которой газ давит на поршеньр – давление газаS – площадь поршняdx - перемещение поршняdV – изменение объема газа Пусть газ находится под поршнем цилиндрического сосуда.
При своем расширении газ совершает работуA по перемещению поршня.
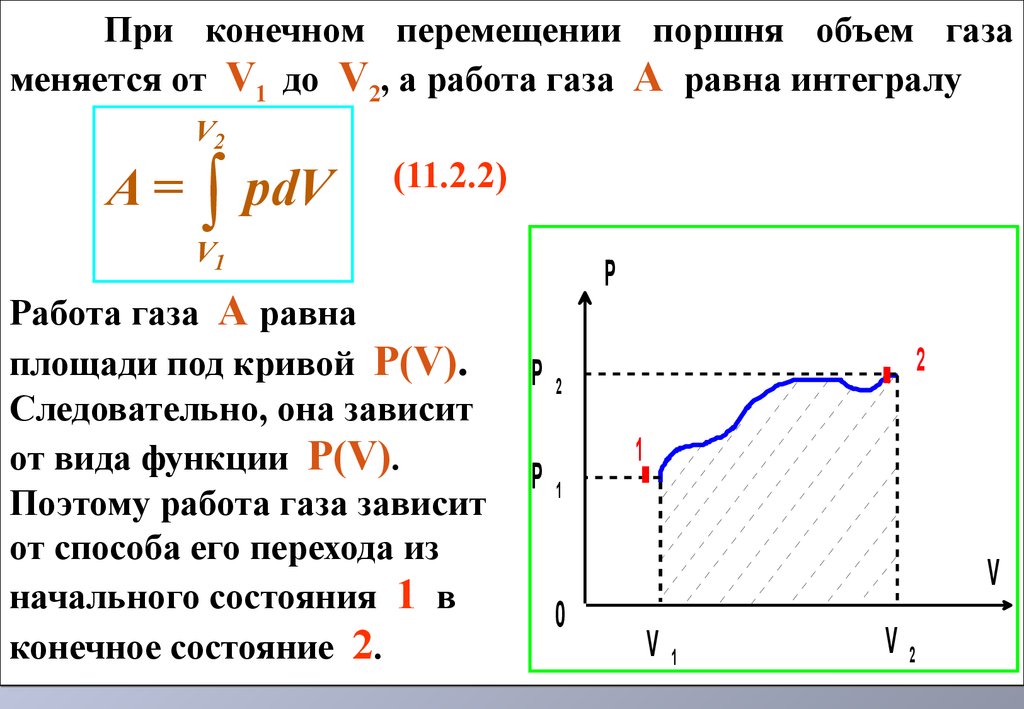
При малом перемещении поршня элементарную работу газа можно записать как d'A = Fdx = pSdx = pdV (11.2.1) где F = pS – сила, с которой газ давит на поршеньр – давление газаS – площадь поршняdx - перемещение поршняdV – изменение объема газа 11.2 Работа газа при изменении объема 11.2 Работа газа при изменении объемаdxP При конечном перемещении поршня объем газа меняется отV1 доV2 , а работа газаA равна интегралу (11.2.2) Работа газаA равна площади под кривой P(V).
Следовательно, она зависит от вида функции P(V).
Поэтому работа газа зависит от способа его перехода из начального состояния1 в конечное состояние2.
При конечном перемещении поршня объем газа меняется отV1 доV2 , а работа газаA равна интегралу (11.2.2) Работа газаA равна площади под кривой P(V).
Следовательно, она зависит от вида функции P(V).
Поэтому работа газа зависит от способа его перехода из начального состояния1 в конечное состояние2.PV0V1V2P1P2.1221V A=pdV Теплоемкость равна количеству теплоты, которое нужно передать телу, чтобы повысить его температуру на1°К (11.3.1) Теплоемкость измеряется в Дж/K°.
Удельная теплоемкость есть количество теплоты, необходимое для нагревания 1 кг вещества на 1° К (11.3.2) гдеm – масса газа.
Удельная теплоемкость измеряется в Дж/(кг·K°).
Теплоемкость равна количеству теплоты, которое нужно передать телу, чтобы повысить его температуру на1°К (11.3.1) Теплоемкость измеряется в Дж/K°.
Удельная теплоемкость есть количество теплоты, необходимое для нагревания 1 кг вещества на 1° К (11.3.2) гдеm – масса газа.
Удельная теплоемкость измеряется в Дж/(кг·K°).
11.3 Теплоемкость идеального газа 11.3 Теплоемкость идеального газаd'QC=dT 1d'Qc=mdT Молярная теплоемкость – количество теплоты, необходимое для нагревания 1 моля вещества на1°К (11.3.3) где = m/M - количество молей вещества.
Молярная теплоемкость измеряется в Дж/(моль·K°).
Молярная теплоемкость – количество теплоты, необходимое для нагревания 1 моля вещества на1°К (11.3.3) где = m/M - количество молей вещества.
Молярная теплоемкость измеряется в Дж/(моль·K°).m 1d'Qc= νdT Теплоемкость зависит от условий измерения.
Различают молярную теплоемкость при постоянном объемеcV и постоянном давленииcP: если газ нагревается при постоянном объеме (11.3.4) если газ нагревается при постоянном давлении (11.3.5) Теплоемкость зависит от условий измерения.
Различают молярную теплоемкость при постоянном объемеcV и постоянном давленииcP: если газ нагревается при постоянном объеме (11.3.4) если газ нагревается при постоянном давлении (11.3.5) V 1d'Qc= νdT P 1d'Qc= νdT Получим выражения для этих теплоемкостей, используя первый закон термодинамики (11.1.1) и формулу для работы газаdA (11.2.1)d Q = dU + pdV Разделив ее наdT и число молей газа находим гдеUm = U/ - внутренняя энергия одного моля газа,Vm = V/ - объем одного моля газа.
Получим выражения для этих теплоемкостей, используя первый закон термодинамики (11.1.1) и формулу для работы газаdA (11.2.1)d Q = dU + pdV Разделив ее наdT и число молей газа находим гдеUm = U/- внутренняя энергия одного моля газа,Vm = V/- объем одного моля газа.mmV ν==MVmm d'QdUdVdUdV =+p=+p νdTνdTνdTdTdT Подставляя в выражения для теплоемкостей (11.3.4), (11.3.5) , получаем (11.3.6а) (11.3.6б) Подставляя в выражения для теплоемкостей (11.3.4), (11.3.5) , получаем (11.3.6а) (11.3.6б) mVVV 1dUdUc== νdTdT mmPPPP 1d'QdUdV c==+p νdTdTdT Опыт показывает, что у газов, свойства которых близки к идеальному газу, теплоемкостьсV практически не зависит от температуры Интегрируя это дифференциальное уравнение и полагая постоянную интегрирования равной нулю, получаемUm = сVT U=сVT (11.3.7) Подставим найденную энергиюUm в формулу длясР (11.3.8) Формула (11.3.8) справедлива для любых газов.
Опыт показывает, что у газов, свойства которых близки к идеальному газу, теплоемкостьсV практически не зависит от температуры Интегрируя это дифференциальное уравнение и полагая постоянную интегрирования равной нулю, получаемUm = сVT U=сVT (11.3.7) Подставим найденную энергиюUm в формулу длясР (11.3.8) Формула (11.3.8) справедлива для любых газов.
mVmVVdU c=dU=cdTdT mmmPVPPP dUdVdV c=+p=c+p dTdTdT Найдем теплоемкость идеального газа .
Для этого используем уравнение состояния идеального газа PV =RT PVm = RT откуда ПоэтомусР = сV+ R (11.3.9) СледовательносР > сV Теплоемкость при постоянном давлениисР больше теплоемкости при постоянном объемесV.
Это связано с тем, что при нагревании идеального газа при постоянном давлении часть теплоты идет на совершение работы газом над внешними телами.
Найдем теплоемкость идеального газа .
Для этого используем уравнение состояния идеального газа PV =RT PVm = RT откуда ПоэтомусР = сV+ R (11.3.9) СледовательносР > сV Теплоемкость при постоянном давлениисР больше теплоемкости при постоянном объемесV.
Это связано с тем, что при нагревании идеального газа при постоянном давлении часть теплоты идет на совершение работы газом над внешними телами.mRTV=P mPdVR=dTP Введем отношение Величина называется постоянной адиабаты.
Тогда можем записать (11.3.10) Внутренняя энергия идеального газа пропорциональна произведению давления на объем.
Введем отношение Величина называется постоянной адиабаты.
Тогда можем записать (11.3.10) Внутренняя энергия идеального газа пропорциональна произведению давления на объем.PVVcR γ==1+cc VmmRRTcU -1-1 RTPV U=νU -1-1
Основы термодинамики 11.1 Первое начало термодинамики При термодинамическом описании свойств макросистем используют закономерности, наблюдающиеся в опытных данных.
Первый закон термодинамики представляет собой закон сохранения энергии, обобщенный на тепловые процессы.
В этот закон входят3 величины : 1) внутренняя энергия макросистемыU 2) работаA 3) теплотаQ Рассмотрим эти величины подробно.
11.1 Первое начало термодинамики При термодинамическом описании свойств макросистем используют закономерности, наблюдающиеся в опытных данных.
Первый закон термодинамики представляет собой закон сохранения энергии, обобщенный на тепловые процессы.
В этот закон входят3 величины :1) внутренняя энергия макросистемыU2) работаA3) теплотаQ Рассмотрим эти величины подробно.
Внутренняя энергия макросистемыU состоит из двух частей: 1) кинетической энергии хаотического движения молекул в системе координат, связанной с центром масс системы 2) потенциальной энергии взаимодействия между молекулами системы При этом кинетическая энергия системы как целого и ее потенциальная энергия во внешнем поле во внутреннюю энергиюU не входят.
Если система состоит из нескольких тел, то ее внутренняя энергия равна сумме внутренних энергий тел и потенциальных энергий взаимодействия между ними.
Внутренняя энергия макросистемыU состоит из двух частей:1) кинетической энергии хаотического движения молекул в системе координат, связанной с центром масс системы2) потенциальной энергии взаимодействия между молекулами системы При этом кинетическая энергия системы как целого и ее потенциальная энергия во внешнем поле во внутреннюю энергиюU не входят.
Если система состоит из нескольких тел, то ее внутренняя энергия равна сумме внутренних энергий тел и потенциальных энергий взаимодействия между ними.
Разобьем макросистему на достаточно большие части.
Поскольку межмолекулярные силы короткодействующие, то потенциальной энергией взаимодействия между частями на границах можно пренебречь.
Поэтому внутренняя энергия всей системы равна сумме внутренних энергий ее частей: U = U1+ U2 + … + UN Об этом свойстве внутренней энергииU говорят, что она является аддитивной величиной.
Разобьем макросистему на достаточно большие части.
Поскольку межмолекулярные силы короткодействующие, то потенциальной энергией взаимодействия между частями на границах можно пренебречь.
Поэтому внутренняя энергия всей системы равна сумме внутренних энергий ее частей: U = U1+ U2 + … + UN Об этом свойстве внутренней энергииU говорят, что она является аддитивной величиной.1234567 Внутренняя энергияU обладает еще одним свойством – она является функцией состояния.
Это значит, что величина внутренней энергииU не зависит от того, каким способом макросистема была переведена в данное состояние.
Поэтому изменение внутренней энергииU при переходе системы из одного состояния в другое состояние равно разности внутренних энергий в конечном и начальном состояниях.
Внутренняя энергияU обладает еще одним свойством – она является функцией состояния.
Это значит, что величина внутренней энергииU не зависит от того, каким способом макросистема была переведена в данное состояние.
Поэтому изменение внутренней энергииU при переходе системы из одного состояния в другое состояние равно разности внутренних энергий в конечном и начальном состояниях.
Внутреннюю энергию макросистемыU можно изменить двумя способами 1) совершив над ней работуA 2) сообщив ей некоторое количество теплотыQ Внутреннюю энергию макросистемыU можно изменить двумя способами1) совершив над ней работуA2) сообщив ей некоторое количество теплотыQ При совершении работыA над макросистемой происходит перемещение внешних к ней тел.
Например, при движении поршня в цилиндре с газом, поршень совершает работуA над газом и изменяет его внутреннюю энергию.
Газ в свою очередь тоже совершает работу над поршнем, обозначим ее черезA.
Из3 - го закона Ньютона следует A = - A Далее работу, совершаемую макросистемой над внешними телами будем обозначать черезA .
При совершении работыA над макросистемой происходит перемещение внешних к ней тел.
Например, при движении поршня в цилиндре с газом, поршень совершает работуA над газом и изменяет его внутреннюю энергию.
Газ в свою очередь тоже совершает работу над поршнем, обозначим ее черезA.
Из3 - го закона Ньютона следуетA = - A Далее работу, совершаемую макросистемой над внешними телами будем обозначать черезA .
С другой стороны передача теплотыQ не связана с перемещением внешних тел.
Передача теплоты происходит при контакте внешних тел с макросистемой.
В этом случае изменение внутренней энергии системыU связано с работой молекул более нагретого тела над молекулами менее нагретого тела.
С другой стороны передача теплотыQ не связана с перемещением внешних тел.
Передача теплоты происходит при контакте внешних тел с макросистемой.
В этом случае изменение внутренней энергии системыU связано с работой молекул более нагретого тела над молекулами менее нагретого тела.
ТеплотаQ равна энергии, переданной системе внешними телами посредством таких микроскопических процессов.
Из 3 - го закона Ньютона следует, что макросистема в свою очередь передает внешним телам количество теплотыQ = -Q ЕслиQ >0 , то тепло передается от внешней среды макросистеме.
ЕслиQ <0 , то тепло отводится от макросистемы, то есть передается от нее внешней среде.
Внутренняя энергия системы может также меняться при облучении электромагнитными волнами.
При этом поглощенная энергия фотонов переходит в энергию возбужденных состояний молекул макросистемы.
ТеплотаQ равна энергии, переданной системе внешними телами посредством таких микроскопических процессов.
Из 3 - го закона Ньютона следует, что макросистема в свою очередь передает внешним телам количество теплотыQ = -Q ЕслиQ >0 , то тепло передается от внешней среды макросистеме.
ЕслиQ <0 , то тепло отводится от макросистемы, то есть передается от нее внешней среде.
Внутренняя энергия системы может также меняться при облучении электромагнитными волнами.
При этом поглощенная энергия фотонов переходит в энергию возбужденных состояний молекул макросистемы.
Из закона сохранения энергии следует , что изменение внутренней энергии системыU при ее переходе из начального состояния1 в конечное состояние2 равно сумме совершенной над системой работы внешних телA и переданного системе теплаQ , то естьU =U2 - U1 =A +Q ПосколькуA = -A , то (11.1.1) Эта формула выражает собой первое начало термодинамики: Количество теплотыQ , переданное системе, идет на приращение ее внутренней энергииU и на совершение работыA над внешними телами.
Из закона сохранения энергии следует , что изменение внутренней энергии системыU при ее переходе из начального состояния1 в конечное состояние2 равно сумме совершенной над системой работы внешних телAи переданного системе теплаQ, то естьU =U2 - U1 =A +Q ПосколькуA = -A, то (11.1.1) Эта формула выражает собой первое начало термодинамики: Количество теплотыQ, переданное системе, идет на приращение ее внутренней энергииU и на совершение работыA над внешними телами. Q=U+A Если U > 0 , то совершенная системой работа меньше полученного количества теплоты, то есть Q > A и наоборот.
Для элементарных процессов, когда два состояния системы близки друг к другу, формула (11.1.1) принимает вид (11.1.2) Штрихи означают, что изменение теплотыdQ и совершенная работаdA зависят от способа перехода системы из одного состояния в другое состояние.
Значит в отличие от внутренней энергииU теплотаQ и работаA не являются функциями состояния.
Поэтому величиныdQ иdА не являются полными дифференциалами , тогда какdU - полный дифференциал.
Если U > 0, то совершенная системой работа меньше полученного количества теплоты, то есть Q > Aи наоборот.
Для элементарных процессов, когда два состояния системы близки друг к другу, формула (11.1.1) принимает вид (11.1.2) Штрихи означают, что изменение теплотыdQ и совершенная работаdA зависят от способа перехода системы из одного состояния в другое состояние.
Значит в отличие от внутренней энергииU теплотаQ и работаA не являются функциями состояния.
Поэтому величиныdQ иdА не являются полными дифференциалами , тогда какdU - полный дифференциал.
d'Q=dU+d'A Пусть макросистема совершает процесс, в ходе которого она периодически возвращается в исходное состояние, тогда ее внутренняя энергияU не будет меняться в таком процессе U = 0 Согласно (11.1.1) в этом случае работаА , совершаемая системой будет равна переданной ей теплотеQ А = Q Следовательно: невозможен периодически действующий двигатель, совершающий работуА большую, чем переданная ему тепловая энергияQ.
Вечный двигатель первого рода невозможен.
Пусть макросистема совершает процесс, в ходе которого она периодически возвращается в исходное состояние, тогда ее внутренняя энергияU не будет меняться в таком процессе U = 0 Согласно (11.1.1) в этом случае работаА , совершаемая системой будет равна переданной ей теплотеQА=Q Следовательно: невозможен периодически действующий двигатель, совершающий работуА большую, чем переданная ему тепловая энергияQ.
Вечный двигатель первого рода невозможен.
ТеплотаQ измеряется в тех же единицах, что энергияU и работаА , то есть в джоулях.
Раньше применялась единица количества теплоты калория.
Калория и джоуль связаны соотношениями 1 кал = 4.18 Дж 1 Дж = 0.24 кал ТеплотаQ измеряется в тех же единицах, что энергияU и работаА , то есть в джоулях.
Раньше применялась единица количества теплоты калория.
Калория и джоуль связаны соотношениями 1 кал = 4.18 Дж 1 Дж = 0.24 кал Пусть газ находится под поршнем цилиндрического сосуда.
При своем расширении газ совершает работуA по перемещению поршня.
При малом перемещении поршня элементарную работу газа можно записать как d'A = Fdx = pSdx = pdV (11.2.1) где F = pS – сила, с которой газ давит на поршеньр – давление газаS – площадь поршняdx - перемещение поршняdV – изменение объема газа Пусть газ находится под поршнем цилиндрического сосуда.
При своем расширении газ совершает работуA по перемещению поршня.
При малом перемещении поршня элементарную работу газа можно записать как d'A = Fdx = pSdx = pdV (11.2.1) где F = pS – сила, с которой газ давит на поршеньр – давление газаS – площадь поршняdx - перемещение поршняdV – изменение объема газа 11.2 Работа газа при изменении объема 11.2 Работа газа при изменении объемаdxP При конечном перемещении поршня объем газа меняется отV1 доV2 , а работа газаA равна интегралу (11.2.2) Работа газаA равна площади под кривой P(V).
Следовательно, она зависит от вида функции P(V).
Поэтому работа газа зависит от способа его перехода из начального состояния1 в конечное состояние2.
При конечном перемещении поршня объем газа меняется отV1 доV2 , а работа газаA равна интегралу (11.2.2) Работа газаA равна площади под кривой P(V).
Следовательно, она зависит от вида функции P(V).
Поэтому работа газа зависит от способа его перехода из начального состояния1 в конечное состояние2.PV0V1V2P1P2.1221V A=pdV Теплоемкость равна количеству теплоты, которое нужно передать телу, чтобы повысить его температуру на1°К (11.3.1) Теплоемкость измеряется в Дж/K°.
Удельная теплоемкость есть количество теплоты, необходимое для нагревания 1 кг вещества на 1° К (11.3.2) гдеm – масса газа.
Удельная теплоемкость измеряется в Дж/(кг·K°).
Теплоемкость равна количеству теплоты, которое нужно передать телу, чтобы повысить его температуру на1°К (11.3.1) Теплоемкость измеряется в Дж/K°.
Удельная теплоемкость есть количество теплоты, необходимое для нагревания 1 кг вещества на 1° К (11.3.2) гдеm – масса газа.
Удельная теплоемкость измеряется в Дж/(кг·K°).
11.3 Теплоемкость идеального газа 11.3 Теплоемкость идеального газаd'QC=dT 1d'Qc=mdT Молярная теплоемкость – количество теплоты, необходимое для нагревания 1 моля вещества на1°К (11.3.3) где = m/M - количество молей вещества.
Молярная теплоемкость измеряется в Дж/(моль·K°).
Молярная теплоемкость – количество теплоты, необходимое для нагревания 1 моля вещества на1°К (11.3.3) где = m/M - количество молей вещества.
Молярная теплоемкость измеряется в Дж/(моль·K°).m 1d'Qc= νdT Теплоемкость зависит от условий измерения.
Различают молярную теплоемкость при постоянном объемеcV и постоянном давленииcP: если газ нагревается при постоянном объеме (11.3.4) если газ нагревается при постоянном давлении (11.3.5) Теплоемкость зависит от условий измерения.
Различают молярную теплоемкость при постоянном объемеcV и постоянном давленииcP: если газ нагревается при постоянном объеме (11.3.4) если газ нагревается при постоянном давлении (11.3.5) V 1d'Qc= νdT P 1d'Qc= νdT Получим выражения для этих теплоемкостей, используя первый закон термодинамики (11.1.1) и формулу для работы газаdA (11.2.1)d Q = dU + pdV Разделив ее наdT и число молей газа находим гдеUm = U/ - внутренняя энергия одного моля газа,Vm = V/ - объем одного моля газа.
Получим выражения для этих теплоемкостей, используя первый закон термодинамики (11.1.1) и формулу для работы газаdA (11.2.1)d Q = dU + pdV Разделив ее наdT и число молей газа находим гдеUm = U/- внутренняя энергия одного моля газа,Vm = V/- объем одного моля газа.mmV ν==MVmm d'QdUdVdUdV =+p=+p νdTνdTνdTdTdT Подставляя в выражения для теплоемкостей (11.3.4), (11.3.5) , получаем (11.3.6а) (11.3.6б) Подставляя в выражения для теплоемкостей (11.3.4), (11.3.5) , получаем (11.3.6а) (11.3.6б) mVVV 1dUdUc== νdTdT mmPPPP 1d'QdUdV c==+p νdTdTdT Опыт показывает, что у газов, свойства которых близки к идеальному газу, теплоемкостьсV практически не зависит от температуры Интегрируя это дифференциальное уравнение и полагая постоянную интегрирования равной нулю, получаемUm = сVT U=сVT (11.3.7) Подставим найденную энергиюUm в формулу длясР (11.3.8) Формула (11.3.8) справедлива для любых газов.
Опыт показывает, что у газов, свойства которых близки к идеальному газу, теплоемкостьсV практически не зависит от температуры Интегрируя это дифференциальное уравнение и полагая постоянную интегрирования равной нулю, получаемUm = сVT U=сVT (11.3.7) Подставим найденную энергиюUm в формулу длясР (11.3.8) Формула (11.3.8) справедлива для любых газов.
mVmVVdU c=dU=cdTdT mmmPVPPP dUdVdV c=+p=c+p dTdTdT Найдем теплоемкость идеального газа .
Для этого используем уравнение состояния идеального газа PV =RT PVm = RT откуда ПоэтомусР = сV+ R (11.3.9) СледовательносР > сV Теплоемкость при постоянном давлениисР больше теплоемкости при постоянном объемесV.
Это связано с тем, что при нагревании идеального газа при постоянном давлении часть теплоты идет на совершение работы газом над внешними телами.
Найдем теплоемкость идеального газа .
Для этого используем уравнение состояния идеального газа PV =RT PVm = RT откуда ПоэтомусР = сV+ R (11.3.9) СледовательносР > сV Теплоемкость при постоянном давлениисР больше теплоемкости при постоянном объемесV.
Это связано с тем, что при нагревании идеального газа при постоянном давлении часть теплоты идет на совершение работы газом над внешними телами.mRTV=P mPdVR=dTP Введем отношение Величина называется постоянной адиабаты.
Тогда можем записать (11.3.10) Внутренняя энергия идеального газа пропорциональна произведению давления на объем.
Введем отношение Величина называется постоянной адиабаты.
Тогда можем записать (11.3.10) Внутренняя энергия идеального газа пропорциональна произведению давления на объем.PVVcR γ==1+cc VmmRRTcU -1-1 RTPV U=νU -1-1




















 Физика
Физика








